基于模態分析的機械聲信號識別*
賀文紅
(海軍裝備部 北京 100071)
1 引言
機械聲音信號中關鍵信息的提取和挖掘對機械故障診斷、機械內部結構分析有著重要的作用。然而,由于聲音傳遞介質復雜性,以及噪聲的不可描述性,使得水下聲音信號中含有大量的不可建模的噪聲,在此情況下,對機械聲音信號的挖掘和提取有效信息就顯得尤為困難。因而在該情形下,對強干擾下的弱信號的有效特征提取就成為提高識別能力的關鍵要素。本論文在一維信號識別的框架下,通過提取水下聲音信號中的深度特征,利用半監督學習的方法,構建適應于機械聲音信號的分類模型,以實現試驗場景下和真實場景下對機械發動機轉速信息的高精度提取和識別。
2 相關原理介紹
2.1 Huang變換
Huang變換[1]是由Norden E.Huang在1998年提出的,用以解決非線性非穩態信號的Hilbert變換(主要是Hilbert變換要求信號的瞬時頻率唯一,這樣通過對信號的空間重構便可以直接通過相位的導數求得具有物理意義瞬時頻率)。他是通過大量的實驗得出,通過對原始信號不斷地求上下包絡,然后用原信號減去包絡平均,通過本征模態的篩選,就可以將原始信號分解成多個本征模態,而這多個本征模態的瞬時頻率基本唯一,從而實現了對原始信號的分解。
Huang變換的主要算法是EMD算法[2~4],其主要原理是根據Norden E.Huang對本征模態的判定來,判定條件如下。
1)信號的上包絡和下包絡的平均值趨近于0;
2)原始信號的極值點個數(包括極大值點個數+極小值點個數)和原始信號同y=0的交點個數之差不能大于1(小于等于1)。
EMD算法的框圖如圖1。
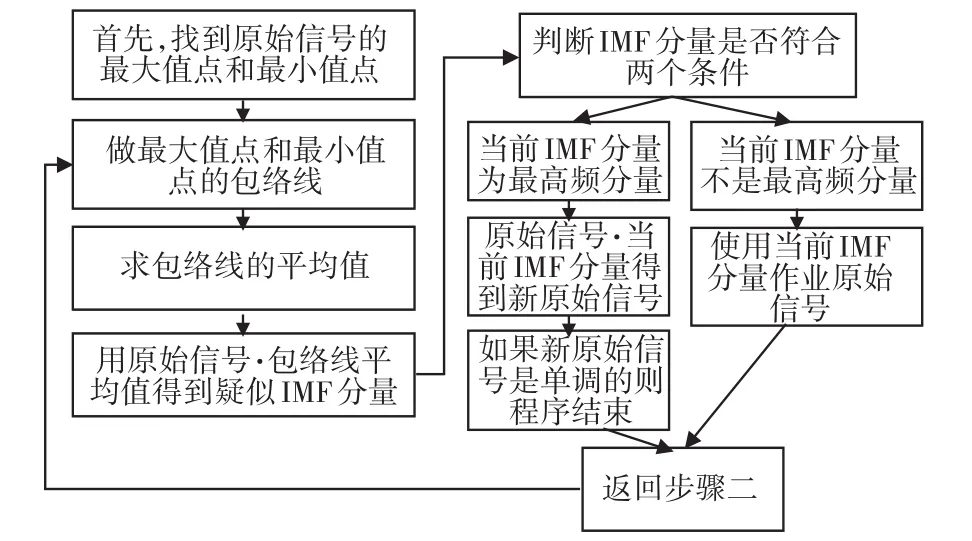
圖1 EMD算法框圖
圖3 到圖5是用EMD算法,對p20的聲音信號的10000個采樣點提取IMF的結果,可以看出,信號的主要的能量集中在前幾個IMF里。
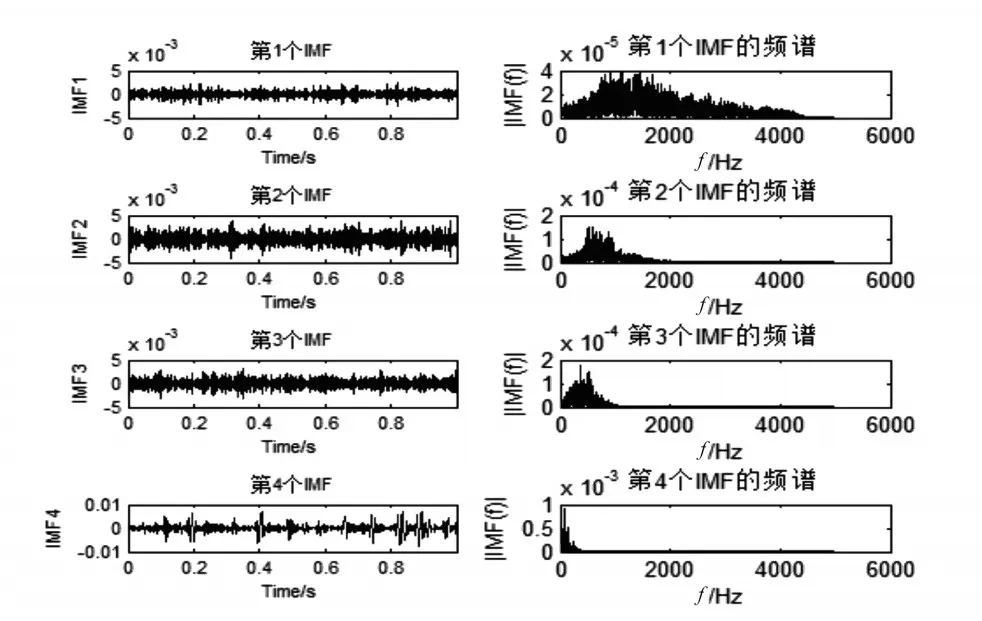
圖2 p20Huang變換后1MF~4IMF及其頻譜示意圖
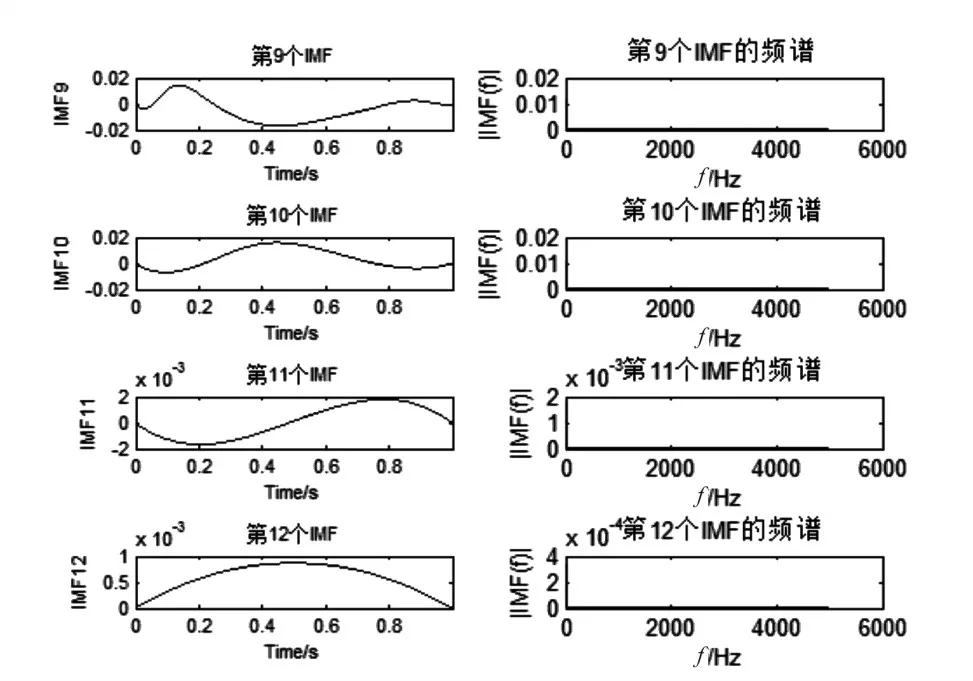
圖3 p20Huang變換后5IMF~8IMF及其頻譜示意圖
2.2 梅爾倒譜系數
在對原始信號做完Huang變換后,對提取的前4個本征模態做梅爾倒譜變換,提取其梅爾倒譜系數。在該分類器中本文主要使用14維的梅爾倒譜系數作為分類的決定性特征。梅爾倒譜是基于仿生學,對人耳分辨聲音的原理進行模擬,將頻譜彎曲,構建出梅爾譜,從而實現對人聲的更好的分辨。倒譜和梅爾頻率倒譜的區別在于,梅爾頻率倒譜的頻帶劃分是在梅爾刻度上等距劃分的,它比用于正常的對數倒頻譜中的線性間隔的頻帶更能近似人類的聽覺系統。這種頻率彎曲可以更好地表示聲音。
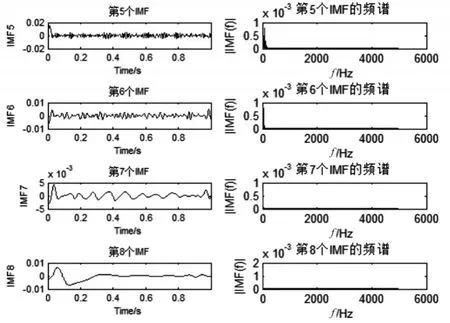
圖4 p20Huang變換后9IMF~12IMF及其頻譜示意圖
提取的過程如圖5所示。

圖5 梅爾倒譜系數提取過程
先對輸入的音頻信號做預處理(預加重、分幀、加窗),然后基于窗函數用快速傅里葉變換對其做短時傅里葉變換,然后對變換后的結果取模長,取對數,最后做離散余弦變換(DCT)得到梅爾倒譜系數,這個過程是用梅爾譜代替頻譜進行變換,而整個變化方式是用求倒譜的變換方式,故而得到的特征不僅具有頻譜的穩定性還有基于人耳識別聲音的生物學原理。
2.3 半監督粗糙模糊拉普拉斯特征映射維數約簡(SSFRLE)
對提取的四個本征模態的梅爾倒譜系數特征,我們采用一種半監督的基于局部的保類流形降維的方法對原始特征降維[5],從而得到新的特征,而所降的維度由PCA自適應的確定。
SSFRLE算法主要思想是先用模糊相似度量構建出該數據集的屬性重要度,然后綜合類信息,利用帶有屬性重要度的數據構建模糊相似矩陣,然后基于該模糊相似矩陣構造近鄰粗糙模糊集,從而確定每一類樣本的隸屬度,然后將隸屬度與核距離組合起來,加上類信息從而構造出權值,如下:

其中xi∈Rm表示第i個數據點,而 Nk(xi)表示i的k近鄰集,μ-NXj(xi)則表示xj的模糊相似類且為模糊矩陣RS中的第i列Xj關于近鄰關系N的下近似在X上的一對模糊集,由擴張原理可知其計算公式如下:
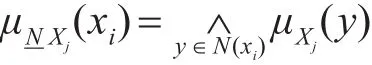
并且,為描述半監督數據集中的監督信息,SSFRLE方法構造了一個類相關圖GC。如果樣本xj的標記信息為 t∈{1,2,…,f},且 RS(xi,xj)可以解釋為樣本xi屬于第t類的隸屬度,令WC=(WiCt)n×f為圖GC的權矩陣:
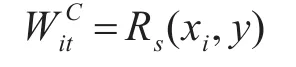
基于移速分析[5],構造如下優化問題:
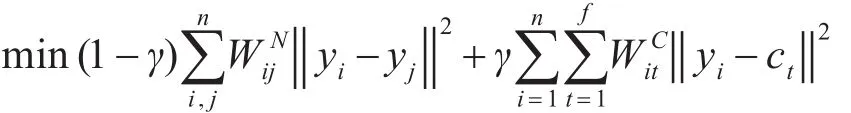
其中,γ是一個實參數且γ∈[0,1],它為了權衡近鄰樣本間的距離與樣本與類中心間的距離對函數值的影響,yi∈Rd表示原始數據xi對應的低維表示,ct表示降維后第t個聚類中心,f表示類數。
整理得:
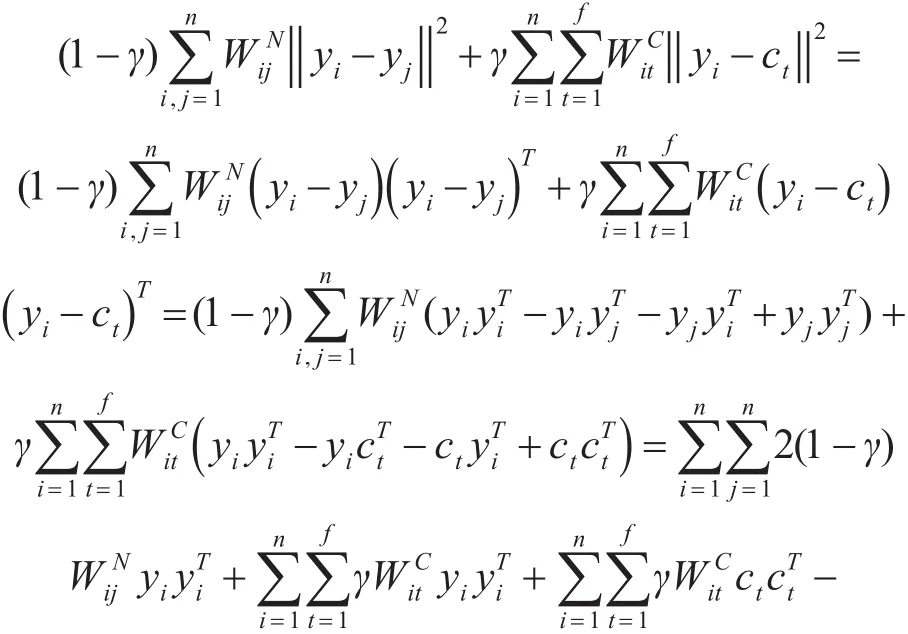
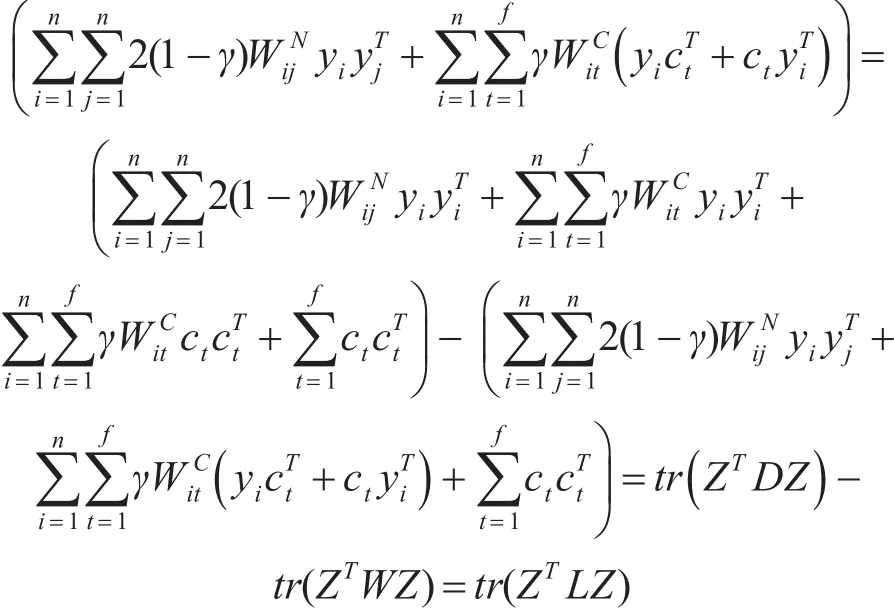
對上述矩陣形式做變換[6],令
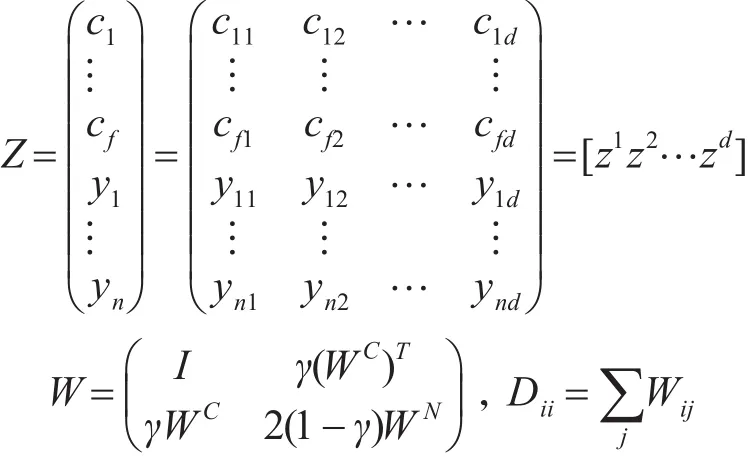
且 D是一個 (f+n)×(f+n)的對角矩陣,L=D-W 是一個(f+n)×(f+n)半正定的拉普拉斯矩陣。
為了確保優化問題有解,加入兩個限制條件[7]:
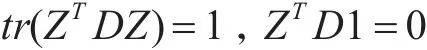
通過拉格朗日乘子法,求上述優化問題,則有:

我們可以得到列向量z1,z2,…,zd是的前d個最小的非負特征值 0≠λ1≤λ2≤…≤λd對應的特征向量,則矩陣[z1z2…zd]的前 f行是數據集 X在低維空間中的類中心[9],矩陣 [z1z2…zd]的后 n 行是數據集X在低維空間中的表示。
2.4 模糊C均值(FCM)
模糊C均值是一種無監督的動態聚類方法[6~9],對于一個數據集,FCM算法需要我們事先規定聚為幾類,假設聚為C類。則對于每個數據點,其屬于某一類的隸屬度可以組成一個模糊分類矩陣,對于此矩陣有如下要求:
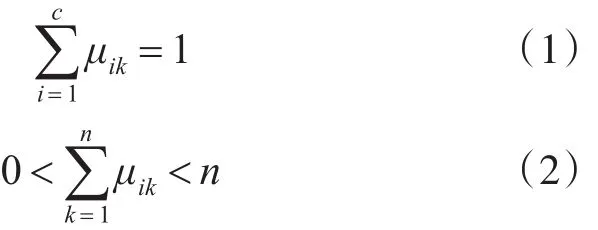
其中μik表示第K個數據屬于第i類的隸屬度,故而式(1)是表示每個數據點屬于所有類隸屬度之和是1,式(2)表示每一類中至少有1個點,至多有n個點。
基于隸屬度便可以依據距離定義能量函數,如式(3):
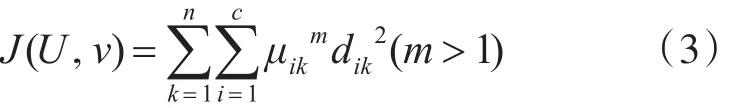
其中第k個點到底i類聚類中心的距離定義為歐氏距離(vij表示第i個聚類中心的第j維):
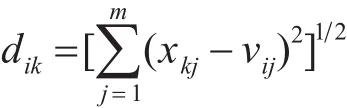
然后用梯度下降法極小化式(3)可得:
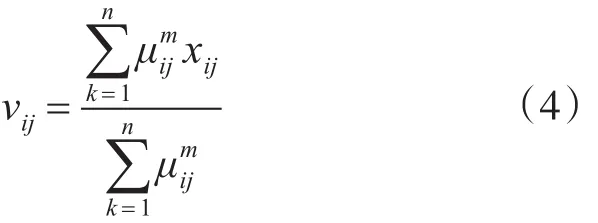
則式(4)即為聚類中心的最優表達式[10~13],采用交叉迭代法來更新聚類中心至最優[14~15]。
3 半監督機械聲音信號的識別方法
本文主要對一維聲音信號處理,提取其多級特征,然后使用模糊C均值(FCM)對所得特征進行聚類,如圖6所示。
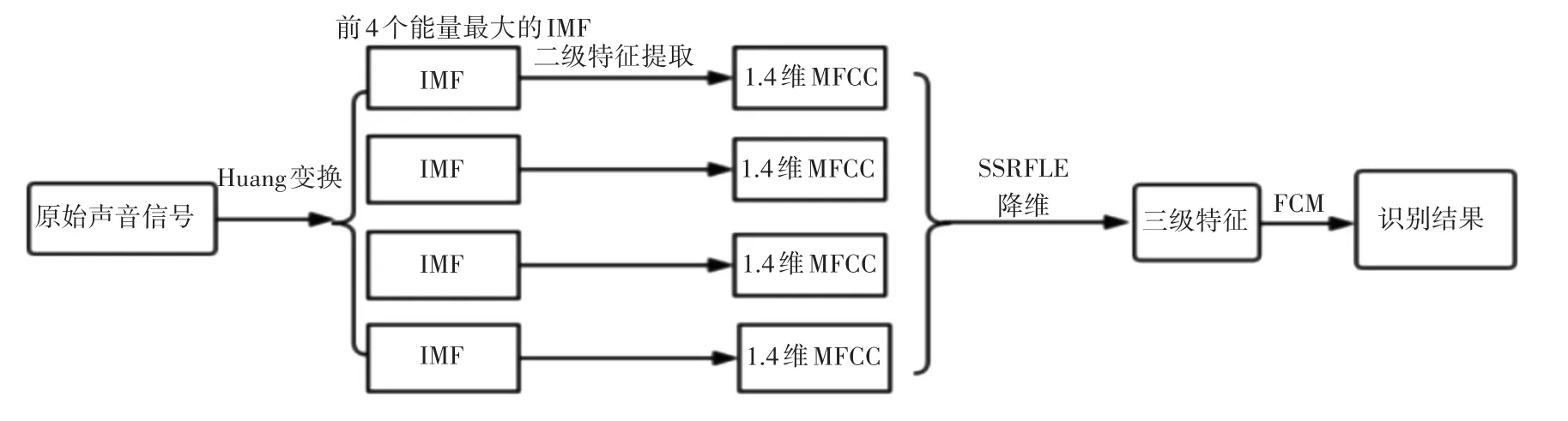
圖6 模型綜述
對于所給信號,本文首先選用Huang變換對每個信道的聲音進行處理,削弱信號中騎行波等對聲音特征提取的影響,并選擇前四個能量最大的本征模態(IMF)作為一級特征。然后,基于聲學中耳朵聽聲原理,對每個IMF提取14維的梅爾倒譜系數(MFCC)作為高維二級特征(維度數為1728)。對于此高維信號,因其所處的數據空間為嵌入到高維空間中的低維流形,因此我們使用半監督模糊粗糙拉普拉斯映射(SSRFLE)對其做流形降維從而構建三級特征。最后使用FCM對其進行聚類,得到數據的識別結果。
為了驗證上述特征提取方式的可行性,本文通過對其特征空間的可視化分析,得出機械聲音信號的深度特征分布情況,如圖7,灰色和黑色分別表示有負載時機械轉速(p20)和無負載機械轉速20(w20)特征空間的第2維和第5維分布情況。
從圖7中可以發現,這兩組數據按照上述模式提取的深度特征成簇狀分布,且分屬于兩個簇中,可以認為在本文所提出的特征提取的框架下,機械聲音信號的本征特征可以很好地提取出來。并且,對于成簇狀分布的特征,采用FCM可以有效地對其進行聚類識別。
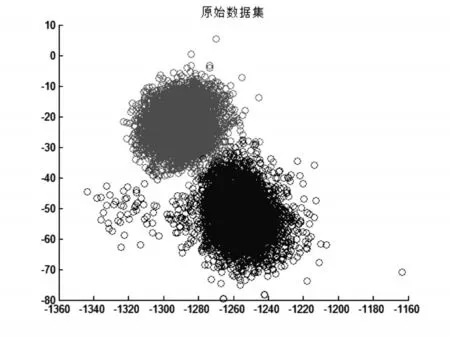
圖7 p20和w20的第2維和第5維特征空間示意圖
4 試驗結果及分析
本文利用真實場景下18聲音接受裝置對機械發動機不同轉速下聲音信號的采樣結果,在采樣頻率為5000Hz下,選取其中連續的100000個采樣點,利用上述框架,分別提取各類數據的深度特征,并使用FCM對所提取的特征進行聚類識別,得到最終的試驗結果如下。
表1和表2分別展示了p0和p20試驗組與其他組各個信號數據的識別精度。通過表1和表2可以發現,本文所提出的識別模型在多數的識別試驗組上有較好的識別精度。而對于組p0-w0組而言,此時試驗組間的區別僅在于是否還有負載發動機的聲音,而此種聲音在強背景噪聲下很難區分,因而在此中情形下,數據本身差異較小,故而在提取其本征特征時,得到的特征空間的分布差異較小,致使最終聚類識別精度較低。
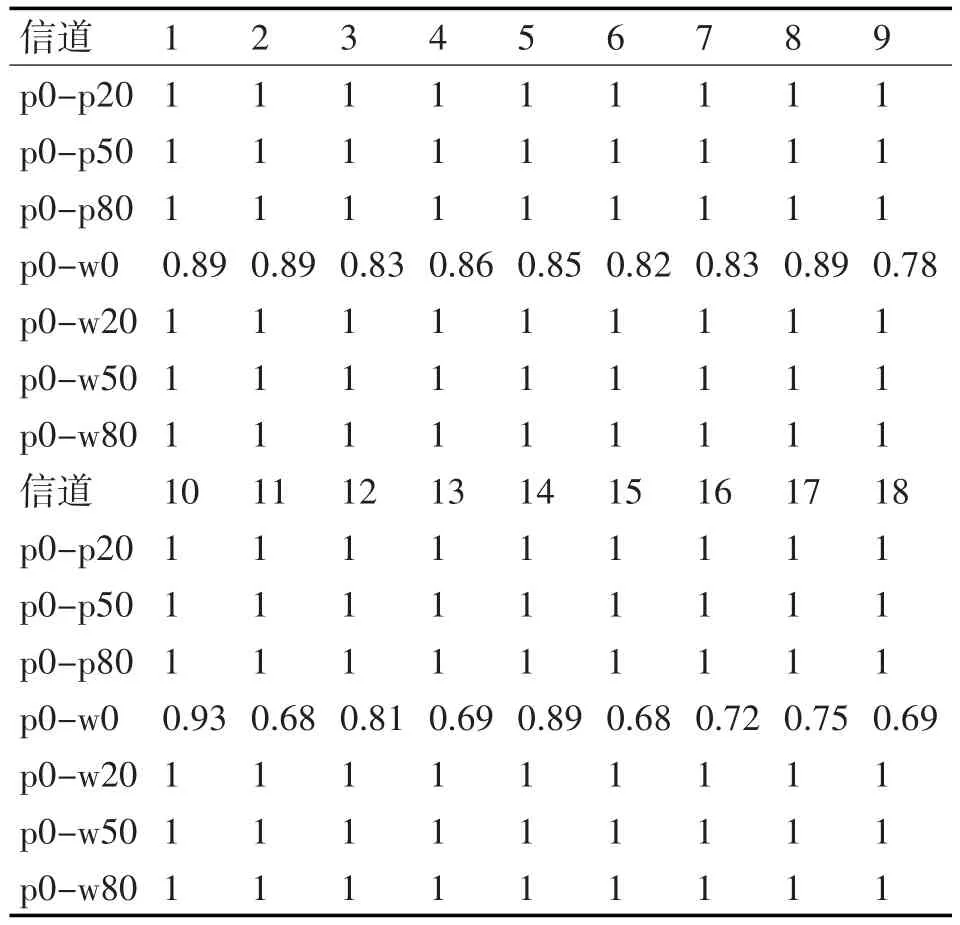
表1 各個接受設備p0試驗組與其他組的識別精度表
對于多個信號融合情況,本文將各個聲音信號接受裝置所搜集的數據按維度排列,得到一個超維的數據列表,然后利用流形學習對其進行維度約減和屬性融合,從而得到更豐富、更符合數據本征特征的數據特征向量。表3分別展示了信號融合前和信號融合后轉速50與轉速80的識別精度,從該表中可以發現,融合后數據的聚類精度相較與未融合時平均提升了0.3,如上分析,在此種數據特征融合下,數據的本征特征得以更好地表達和刻畫。
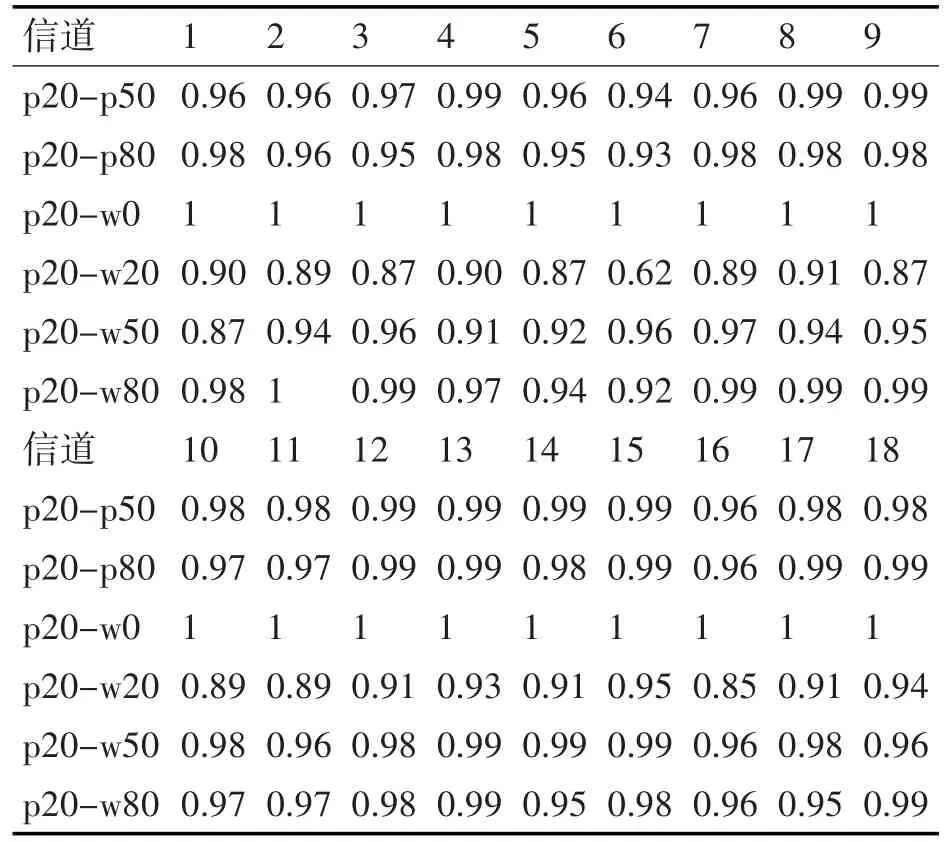
表2 各個接受設備p20試驗組與其他組的識別精度表
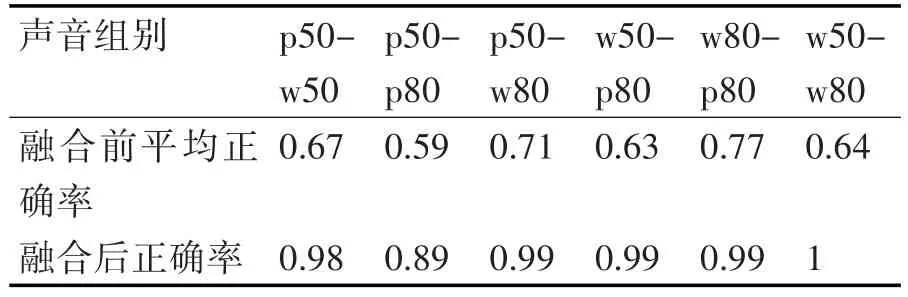
表3 各類接受信號融合后轉速50與轉速80的識別精度表
5 結語
基于半監督流形學習的機械聲音信號識別方法可以對于真實場景下機械聲音信號的識別有較強的性能。對于單一信道的聲音識別,通過該方法提取的特征在某些試驗組中存在著分離性較差的情況,可能原因是:不同的接收器接受到的聲音受混響反射等因素的影響,導致單個接收器接受到的聲音信息失真。將所有的接受器接受到的信號組合起來,增大了數據的信息量,能在一定程度上減少信號的失真比例,從而能更好地實現數據的分離。另外,本文通過非線性的半監督流形降維,利用數據標號信息,在一定程度上將數據類與類拉開,從而增大數據的可分性。此方法是考慮半監督樣本領域內數據的類信息,通過該標號情況構造一個近鄰粗糙模糊集,在領域內我們采用的是取最小隸屬度原則,這樣對一個無標號信息的樣本就可以用其領域信息來判讀其屬于各類的隸屬度。

