抗陣列流形誤差的穩健低旁瓣波束優化設計*

董鵬飛

（杭州應用聲學研究所 杭州 310012）

1 引言

衡量一個波束形成器好壞的指標主要有主瓣寬度、旁瓣級、陣增益、魯棒性等。這些指標在某一方面反映著波束形成器的性能，但是每個指標并不是獨立的，上述指標之間是相互關聯相互制約的，有些甚至是矛盾的。如何在這些相互制約的指標之間尋求一個最佳的折衷，就是波束優化設計［1］研究的內容。在波束優化設計研究的過程中，出現了大量的提高陣列穩健性的方法，減小因為誤差引起的性能下降。其中，當波達方向不確定時，運用線性約束最小方差波束形成法進行波束優化，對于觀察方向失配的情況，具有較好的魯棒性［2］。對于另一類因為導向矢量失配（如陣列擾動、陣列流形模型誤差等）引起的陣列性能下降問題，常用二次波束約束波束形成法去解決。該方法是通過對陣列加權向量的Euclidean范數進行二次約束來實現的。目前，運用二階錐規劃（SCOP）方法［3～4］能夠很簡單地解決該類問題，因此該類方法得到了廣泛應用。

2 抗陣列流形誤差的穩健低旁瓣波束形成

實際的工程應用中，一般無法知道精確的陣列流形向量。在陣列流形存在誤差的情況下，如果仍然采用理想方法設計權向量，并利用這個權向量去做波束形成，那么得到的波束圖會出現嚴重的畸變，波束旁瓣常常會升的很高。為解決這一問題，通常采用抗陣列流形誤差的旁瓣控制波束設計方法［5］。這個方法是通過對加權向量的范數施加一個約束，來提高波束形成器的穩健性，如：‖‖w≤?0。然而，在運用該方法的過程中，往往無法根據陣列流形的不確定范圍來計算最優加權向量的約束值?0。

實際的陣列流形和理想的陣列流形之間總是存在誤差的，對此我們將真實的陣列流形

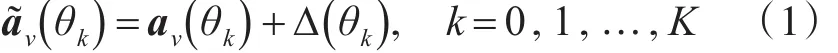
其中，av(θk)表示理想的陣列流形，Δ(θk)表示陣列流形誤差，M表示陣元數目。真實的陣列流形矢量 a?v(θk)在實際應用中往往是未知的，它和理想條件下的陣列流形矢量av(θk)之間是有誤差的，且這個誤差Δ(θk)是未知的復向量。

對于理想的最低旁瓣波束形成器，即在給定主瓣寬度的條件下，使旁瓣級最低［6］。主瓣寬度越寬，能夠獲得的旁瓣級越低。理想最低旁瓣波束形成可以表達為約束優化求解問題，如下：

式中，U(θ)表示陣列流形不確定集。真實的陣列流形矢量被u替代，從而使得上式所表述的低旁瓣波束優化問題能夠轉化為二階錐規劃問題［7～8］，利用Matlab中的SeDuMi工具箱很容易求解［9］。

2.1 穩健低旁瓣波束形成

通常在進行低旁瓣波束設計時，重點研究的是波束主瓣與旁瓣級的問題，并不關注波束形成的穩健性。然而在工程實踐中，常常希望陣列的波束與期望波束相比較，不發生畸變，這就需要在進行低旁瓣波束設計時，增加波束穩健性的約束。波束穩健性約束方法［10］有很多，其中白噪聲增益約束法相對比較簡單，該方法的數學表述為

式中，δ為陣列加權向量范數的上界。

同樣也可以對陣列流形誤差Δ(θk)施加約束，表示如下：

式中，εk為陣列流形誤差的范數，且εk＜＜0。則陣列流形不確定集U(θ)可以表述為橢圓不確定集U2(θ)：

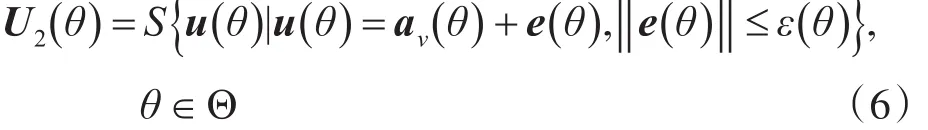
則有u(θ0)∈U2(θ0)。下面以2-范數約束為例，進一步研究穩健性約束優化方法。

式（3）的約束條件可作以下變換：

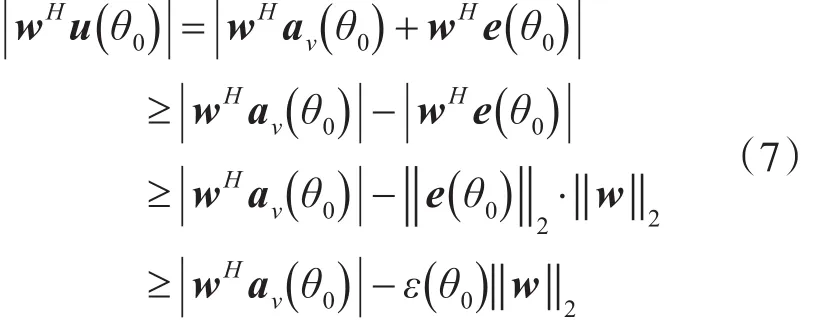
上式取等號的條件為

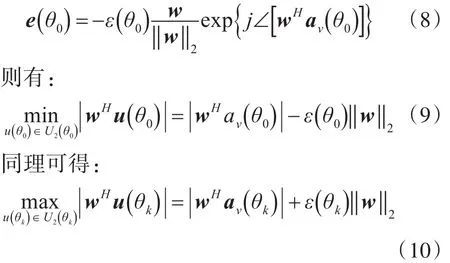
上式成立的條件為

其中代價函數是對旁瓣的設計要求，而約束條件是期望方向的設計要求。該優化問題不是凸優化問題，但是可以通過轉換，將其變成凸優化問題。由于對權向量w進行任意相位的旋轉，的值不發生變化，因此，假設wopt是式（13）的一個解，我們可以對其進行相位旋轉，直到為實數，而不影響代價函數的值。由上述分析可知，式（13）的一個解可以寫成：

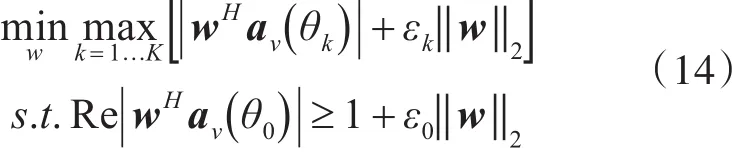
上式所表述的問題即為基于L2（2-范數）準則生成的凸優化問題，稱之為 L2方法［11～12］，將其轉換為二階錐規劃的形式即可利用SeDuMi工具箱很容易求解。

上面是在假設已知陣列流形誤差范數的上界條件下，利用2-范數約束得到的L2方法。還有一種情況，可以假設陣列流形向量誤差的每個元素的上界已知，可以利用1-范數約束推導的到L1方法。基于L1（1-范數）準則的設計原理同L2方法基本類似，在此不做贅述，直接給出其表達式：

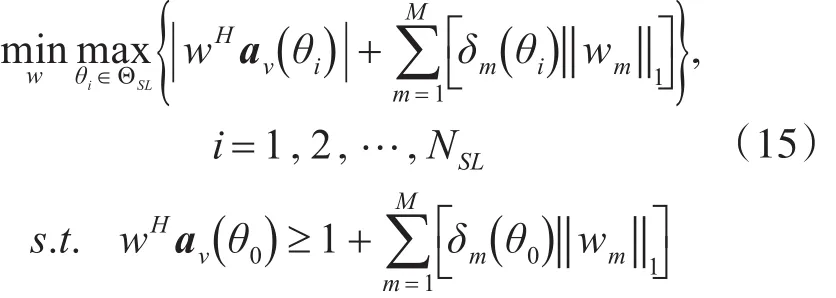
式中，δm為陣列流形向量誤差每個元素的上界，θ0表示的是期望方向，而θi是旁瓣區域所對應的角度。

2.2 仿真分析

工程實踐中，陣列流形向量不可能是理想的，有很多原因會引起陣列流形向量的誤差，很典型的就是陣元的位置誤差。我們以圖1所示的16元擴展陣為例做簡單分析，假設陣元誤差標準差為0.02時，陣元實際位置和理想位置的關系如圖1。

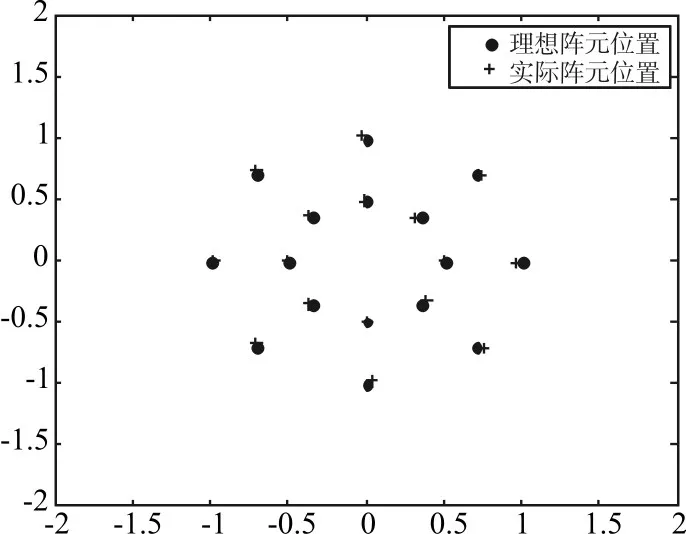
圖1 理想陣元位置和實際陣元位置對比

由于實際中陣列的尺寸一般較大，將會導致實際陣元位置嚴重偏離理想陣元位置，如此大的陣元位置誤差，勢必對波束優化設計造成較大的影響。為直觀說明陣元位置誤差對穩健波束形成的影響，利用該16元擴展陣進行說明。當陣元位置誤差的標準差為0.01、0.015、0.02和0.025，波束形成情況如圖2～圖5。

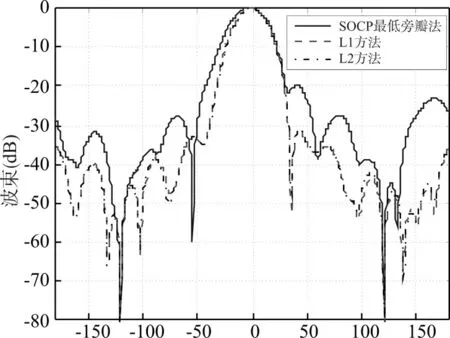
圖2 標準差為0.01時的陣列指向性圖

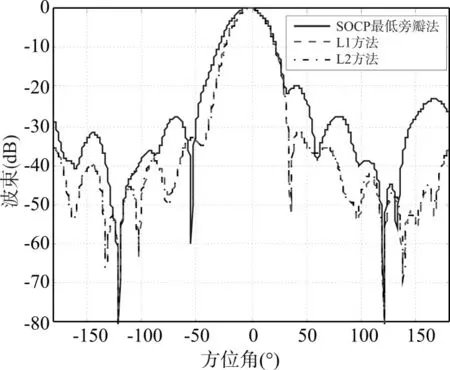
圖3 標準差為0.015時的陣列指向性圖

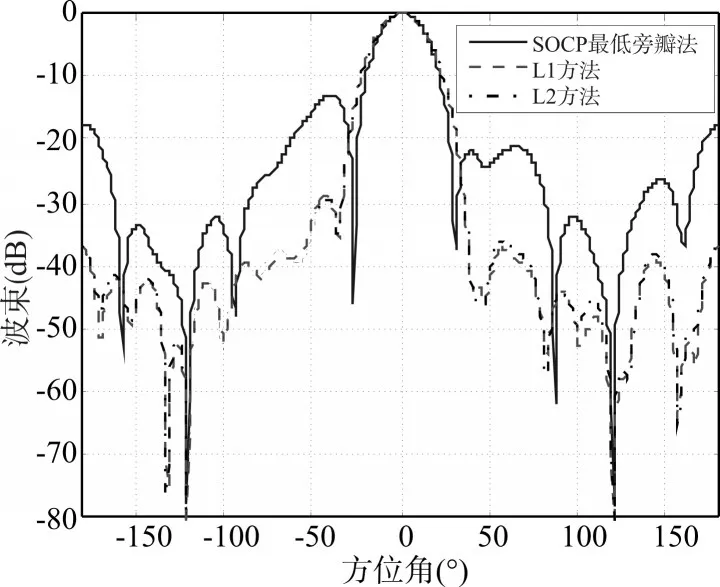
圖4 標準差為0.02時的陣列指向性圖

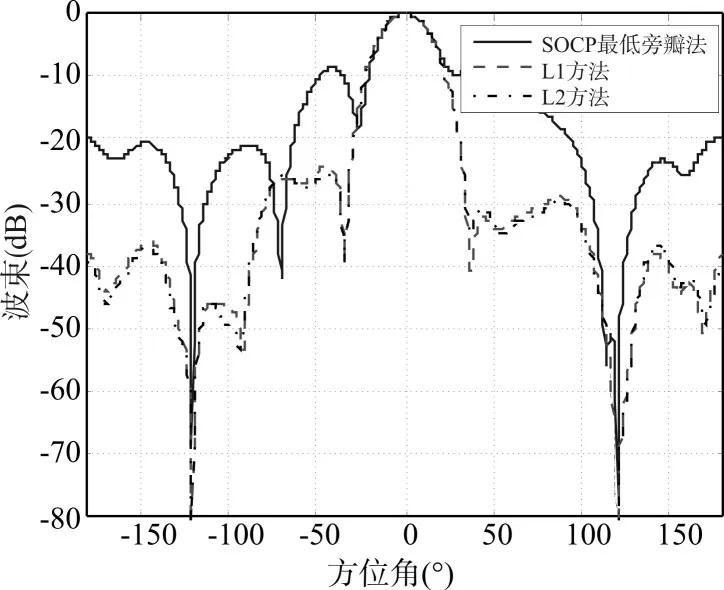
圖5 標準差為0.025時的陣列指向性圖

分析以上四種位置誤差情況下陣列波束可以看出，當陣元位置誤差越來越大時，采用SOCP最低旁瓣法（即理想最低旁瓣法）形成的波束性能越來越差，波束輸出與期望波束差別較大，特別體現在旁瓣級上，旁瓣變得較高，達到了-10dB（相同條件下，在陣元位置誤差為0.01的情況下旁瓣級為-28dB）。利用L1方法和L2方法設計的波束基本一致，具有較強的穩健性，具體表現為當陣元位置誤差越來越大時，其波束響應的旁瓣級也會相應升高，但是基本上是在-30dB左右變化，遠遠低于理想最低旁瓣法設計的波束。這一結果驗證了抗陣列流形誤差的穩健性波束形成設計L1方法和L2方法具有較好的穩健性。

3 結語

本文從實際應用中所面臨的問題（在無法精確知道陣列流形向量的情況，將導致波束形成器性能的改變）出發，針對引起波束形成誤差的原因，分析了抗陣列流形誤差的穩健低旁瓣波束形成方法—L1方法和L2方法。最后在16元擴展陣的條件下分別對SOCP的L1方法和SOCP的L2方法進行了仿真實驗，驗證了抗陣列流形誤差的穩健性波束優化設計L1方法和L2方法具有良好的穩健性，能夠獲得較窄的主瓣和更低的旁瓣級。