Post李超代數(shù)結(jié)構(gòu)的性質(zhì)

王 旭,魏 竹,張慶成

(東北師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,長春 130024)

Post李代數(shù)[1]與Yang-Baxter方程的解[2]、Rota Baxter代數(shù)[2]、LR代數(shù)[3]以及左對稱代數(shù)[4]等密切相關(guān).目前,關(guān)于post李代數(shù)的研究已取得了許多成果[1,5-8]: 文獻(xiàn)[1]證明了post李代數(shù)作為交換環(huán)上三角代數(shù)的Ksozul對偶有重要的代數(shù)性質(zhì);文獻(xiàn)[5]給出了post李代數(shù)的結(jié)構(gòu)和半單李代數(shù)的廣義導(dǎo)子；文獻(xiàn)[6]驗(yàn)證了post李代數(shù)與李群上冪零仿射作用之間的聯(lián)系.但目前關(guān)于post李超代數(shù)的研究結(jié)果較少[9],本文研究post李超代數(shù)結(jié)構(gòu)的性質(zhì),給出post李超代數(shù)與其他超代數(shù)之間的聯(lián)系.

定義1[9]若上的超向量空間V有兩個雙線性映射·和{,},使得(V,{,})是李超代數(shù),且滿足下列條件：

則稱(V，·,{，})為post李超代數(shù).

引理1[9]設(shè)(V,·,{,})是一個李超代數(shù),定義[x，y]=x·y-(-1)|x||y|y·x+{x,y},則(V,[,]) 是李超代數(shù).

定義2[9]設(shè)(G,N )是一對具有底空間V的李超代數(shù),其中N=(V,{,}),G=(V,[,]).若V上有一個雙線性映射·,使得對?x,y,z∈V,滿足下列關(guān)系式:

則稱·為(G,N )上的post李超代數(shù)結(jié)構(gòu).

顯然N=(V,·,{,})是post李超代數(shù),G=(V,[,])是李超代數(shù).

命題1令(V,·,{,})是post李超代數(shù),定義

[x，y]=x·y-(-1)|x||y|y·x+{x,y},

則有

[x,y]·z=x·(y·z)-(-1)|x||y|y·(x·z).

證明:

命題2按上述定義,令·是(G,N )上post李超代數(shù)結(jié)構(gòu),則對?x,y,z∈V,下列等式成立:

{x,y}·z=(-1)|x||y|(y·x)·z-(-1)|x||y|y·(x·z)-(x·y)·z+x·(y·z);

(6)

z·[x,y]=z·(x·y)-(-1)|x||y|z·(y·x)+z·{x,y};

(7)

證明：由定義1可直接得式(6).由定義2有x·y-(-1)|x||y|y·x=[x,y]-{x,y},在等式兩端同時(shí)用z作用,則有

z·[x·y]=z·(x·y)-(-1)|x||y|z·(y·x)+z·{x,y}.

即式(7)得證.由

整理后即得式(8).

由Jacobi等式有

即式(9)得證.又由Jacobi等式有

再由式(9),有

即式(10)得證.

命題3設(shè)·是(G,N )上的post李超代數(shù)結(jié)構(gòu),且由x·y=0給出,則有(V,{,})=(V,[,]).

證明: 因?yàn)閤·y=0,所以有[x,y]={x,y},即(V,{,})=(V,[,]).

命題4若n是可交換的,則由(G,N )上post李超代數(shù)結(jié)構(gòu)可得到G上的一個左對稱超代數(shù)結(jié)構(gòu).

證明: 因?yàn)閚是可交換的,所以有{x,y}=0.由式(1)可得

(-1)|x||y|(y·x)·z-(-1)|x||y|y·(x·z)=(x·y)·z-x·(y·z),

由式(3)和式(4)分別得

x·y-(-1)|x||y|y·x=[x,y], [x,y]·z=x·(y·z)-(-1)|x||y|y·(x·z).

命題5若G是可交換的,則由(G,N )上的post李超代數(shù)結(jié)構(gòu)可得N上的一個LR超代數(shù)結(jié)構(gòu).

證明: 因?yàn)镚是可交換的,所以有[x,y]=0.由式(3)有{x,y}=(-1)|x||y|y·x-x·y.由式(4)有x·(y·z)=(-1)|x||y|y·(x·z).將{x,y}=(-1)|x||y|y·x-x·y代入式(5)得

又因?yàn)閤·(y·z)=(-1)|x||y|y·(x·z),所以有

從而(x·y)·z=(-1)|z||y|(x·z)·y.

命題6設(shè)(G,N )是一對post李超代數(shù),令λ?{0,1,-1},則可定義(G,N )上post李超代數(shù)結(jié)構(gòu)為x·y=λ[x,y]當(dāng)且僅當(dāng){x,y}=(1-2λ)[x,y],且G,N均為至多階為2的冪零李超代數(shù).

證明: 假設(shè)x·y=λ[x,y]是(G,N )上post李超代數(shù)結(jié)構(gòu),則由式(3)可得

λ[x,y]-(-1)|x||y|λ[y,x]=[x,y]-{x,y},

于是

由式(4)及Jacobi等式,有

又因?yàn)棣?{0,1,-1},所以[[x,y],z]={{x,y},z}=(x·y)·z=0.

設(shè)(G,N )是一對至多階為2的冪零李超代數(shù),滿足{x,y}=(1-2λ)[x,y],x·y=λ[x,y],則有

因?yàn)閤·y=λ[x,y],所以有

又因?yàn)?-1)|x||z|λ[[x,y],z]=(-1)|x||z|λ2[[x,y],z],所以

[x,y]·z=x·(y·z)-(-1)|x||y|y·(x·z).

當(dāng)λ≠1/2時(shí),令{x,y}=μx·y,μ=(1-2λ)/λ,則

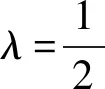
注1當(dāng)λ=0時(shí),有x·y=0,[x,y]={x,y},由命題3可知(V,{,})=(V,[,]).當(dāng)λ=1時(shí),有x·y=[x,y]=-{x,y},此時(shí)x·y是(G,-G)上的post李超代數(shù)結(jié)構(gòu).

命題7設(shè)(G,N )是一對post李超代數(shù),令μ?{0,-1,-1/2},則可定義(G,N )上的post李超代數(shù)結(jié)構(gòu)為x·y=μ{x,y}當(dāng)且僅當(dāng)[x,y]=(1+2μ){x,y},且G,N均為至多階為2的冪零李超代數(shù).

證明: 令x·y=μ{x,y}是(G,N )上的post李超代數(shù)結(jié)構(gòu),由式(3)可得

其中μ?{0，-1，-1/2}.記x·y=λ[x,y](λ≠0),則有

所以[[x,y],z]={{x,y},z}=(x·y)·z=0.

反之,[x,y]=(1+2μ){x,y},且G,N均為至多階為2的冪零李超代數(shù),x·y=μ{x,y},則有

記x·y=λ[x,y],λ=μ/(1+2μ),其中μ?{0,-1,-1/2},則有

所以[x,y]·z=x·(y·z)-(-1)|x||y|y·(x·z).又因?yàn)?/p>

所以x·{y,z}={x·y,z}+(-1)|x||y|{y,x·z}.

命題8令ρ?{0,1},且{x,y}=ρ[x,y],則·是(G,N )上post李超代數(shù)結(jié)構(gòu)當(dāng)且僅當(dāng)下列等式成立:

證明: 設(shè)·是(G,N )上的post李超代數(shù)結(jié)構(gòu),由式(3)可知

[x,y]-{x,y}=x·y-(-1)|x||y|y·x,

又因?yàn)閧x,y}=ρ[x,y],所以有x·y-(-1)|x||y|y·x=(1-ρ)[x,y],即式(11)得證.

將式(11)等號兩端同時(shí)用z作用,有

(1-ρ)[x,y]·z=(x·y)·z-(-1)|x||y|(y·x)·z,

即

(1-ρ)(x·(y·z)-(-1)|x||y|y·(x·z))=(x·y)·z-(-1)|x||y|(y·x)·z,

式(12)得證.

因?yàn)閧x,y}=ρ[x,y],所以

又由式(11)有

即式(13)得證.

反之,由式(11)有

x·y-(-1)|x||y|y·x=[x,y]-ρ[x,y]=[x,y]-{x,y},

即式(3)成立.由

(1-ρ)[x,y]·z=(x·y-(-1)|x||y|y·x)·z=(x·y)·z-(-1)|x||y|(y·x)·z,

及式(12)有

(1-ρ)[x,y]·z=(1-ρ)(x·(y·z))-(-1)|x||y|(1-ρ)y·(x·z),

從而有[x,y]·z=x·(y·z)-(-1)|x||y|y·(x·z),即式(4)成立.又由式(11)有

再由式(13)有

(1-ρ)x·[y,z]=(1-ρ)[x·y,z]+(-1)|x||y|(1-ρ)[y,x·z],

所以

ρx·[y,z]=ρ[x·y,z]+(-1)|x||y|ρ[y,x·z],

即x·{x,y}={x·y,z}+(-1)|x||y|{y,x·z},即式(5)成立.

注3當(dāng)ρ=1時(shí),有[x,y]={x,y}.

定義3設(shè)·為(G,N )上的post李超代數(shù)結(jié)構(gòu),若滿足[x,y]={x,y},且下列等式成立:

則稱·為(G,N )上的交換post李超代數(shù)結(jié)構(gòu).

命題9若在(G,N )上存在交換post李超代數(shù)結(jié)構(gòu)且[x,y]=0,則G=N是交換結(jié)合post李超代數(shù).

證明: 設(shè)·為(G,N )上的交換post李超代數(shù)結(jié)構(gòu),由定義3知[x,y]={x,y},所以有G=N.由式(14)知

x·(y·z)=(-1)|z||y|x·(z·y),y·(x·z)=(-1)|y|(|z|+|x|)(x·z)·y,

從而有(-1)|x||y|y·(x·z)=(-1)|y||z|(x·z)·y,于是

(-1)|z||y|x·(z·y)=x·(y·z)=(-1)|x||y|y·(x·z)=(-1)|y||z|(x·z)·y,

所以x·(z·y)=(x·z)·y.