受媒體影響的謠言傳播模型

沈慶磊 鄧月

摘 ?要： 根據謠言傳播機理，提出了受媒體影響的謠言傳播的SIR（無知者-傳播者-免疫者）模型，并分別用確定性模型和隨機模型來建模。求出了確定性模型中謠言的平衡點，并對平衡點的穩定性作了詳細分析。仿真結果表明，所提出的模型能正確地反映謠言信息傳播的趨勢，較為準確地描述謠言的傳播過程。

關鍵詞： 媒體; 隨機微分方程; SIR; 謠言傳播; 平衡點

中圖分類號：TP391 ? ? ? ? ?文獻標志碼：A ? ? 文章編號：1006-8228（2019）11-11-04

Abstract： According to rumor spreading mechanism， this paper propose the media-affected SIR （Susceptible Infected Recovered ） model of rumors spread， the deterministic model and stochastic model are used respectively for modeling. The equilibrium point of rumour in deterministic model is obtained and the stability of the equilibrium point is analyzed in detail. The simulation results show that the proposed model can correctly reflect the trend of the rumors spreading and accurately describe the process of rumors spreading.

Key words： media; stochastic differential equation; SIR; rumour spreading; equilibrium

0 引言

謠言是社會交流的一種重要形式，它們的傳播在各種各樣的人類事務中扮演著重要的角色。謠言的傳播會影響一個國家的公眾輿論[1]，影響社會經濟[2-3]，也會造成整個社會的恐慌[4-6]。有限的謠言傳播并不可怕，但是廣為傳播的有相當規模的謠言頗有破壞力，極易引起社會騷亂。2010年12月22日某媒體曝出不實消息，稱無根豆芽可致癌，“毒豆芽”事件一經出現，隨即引起社會的廣泛關注和流傳。各大網絡平臺也經常會曝出某某明星離婚事件，消息一經發出，便被人們廣泛議論和傳播。

目前，國內有一些學者對突發謠言問題進行了研究，蘭月新對網絡中突發的SIR輿情謠言模型及其參數進行了分析[7]。王超等人在SIR模型的基礎上提出了具有潛伏狀態的信息傳播模型，并刻畫了信息傳播過程隨時間的演化規律[8]。在經典的謠言傳播模型上增加了冬眠者這一類新的節點，并討論了傳播的域值和謠言的最終傳播量兩者之間的關系[9]。考慮了引入傳播媒介對謠言的傳播起到加速的作用，作者用平均場理論對謠言的動力學行為進行了研究[10]。

以上模型大多數是基于謠言的信息傳播進行理論建模，而實際情況下，謠言會受到外界環境的影響，比如媒體對謠言的傳播會有一定的防控作用。另外模型幾乎都是在確定性模型下建立的，考慮的都是節點的平均狀態，沒有結合實際情況，一些隨機因素都沒有考慮進來。首先，根據謠言傳播機理我們分別用確定性模型和隨機模型來描述謠言傳播的特征，其次在確定性模型中我們對謠言模型的平衡點及穩定性進行了研究，最后在數值模擬中分析了這兩種模型的動力學行為以及模型中的參數對謠言傳播的影響。

1 謠言信息傳播機制和模型

1.1 謠言信息傳播機制

謠言傳播的前提是人們直接與傳播者接觸[11]，謠言傳播的機制與傳染病是一致的。為了更清楚地介紹謠言傳播的模型，我們把所有的節點分成三類，用N=S（t）+ I（t） +R（t）來表示，并認為它們是封閉的，不考慮出生和死亡等因素。其中N是總人數，S（t）表示未接收到消息的無知者，I（t）表示傳播謠言的人，R（t）表示不再傳播謠言對謠言已經免疫的人。

根據以上謠言信息傳播過程，SIR模型的規則如圖1所示。

對SIR模型的假設如下：

⑴ 當一個傳播者接觸一個無知者時，無知者以一定的概率變成傳播者，μ1是自身的接觸率，μ2是受媒體影響的接觸率（0<μ1<1， 0<μ2<1）。

⑵ 當一個傳播者接觸一個免疫者時，傳播者以δ的概率變成免疫者，另一方面由于遺忘機制或者傳播者對謠言失去興趣時他們會以α的概率停止轉發謠言。

1.2 確定性模型

從以上討論中我們可以看到平衡點[S?，0，R?]總是存在的并且有多個值。R是一個關鍵域值決定這個平衡點的穩定性。定理1說明無知者是否滅絕不取決于初始無知者的數量。

1.3 隨機微分方程

確實性模型是一種理想的模型，而在現實的謠言系統中，隨機因素的干擾是無處不在的，因為謠言的傳播與個人心理，習慣，感知控制，信息素養和動機都有關，這種干擾在數學上用“白噪聲”來描述，一般來說，確定性模型是隨機模型的一種特例。因此，在實際問題中忽略掉系統的隨機性，用確實性模型來研究謠言的系統行為是不準確的。通過這個方法我們根據公式（3）產生如下的隨機微分方程：

2 數值模擬

2.1 確定性微分方程的動態分析

到目前為止，我們研究了謠言傳播機制和受媒體影響后的謠言傳播模型，并對它的確定性模型動態性進行了分析。為了便于對我們的數學結果的解釋，我們繼續通過數值模擬來研究它。首先，讓我們分別研究這三種節點隨時間的演變趨勢。假設初始狀態是N=1000， S=990， I=10， R=0， μ1=0.02，μ2=0.0018， α=0.005， b=10， δ=0.007。

2.1.1 三類節點的變化趨勢

三類節點的變化趨勢如圖2所示，它們體現的是節點的平均特性，無知者和傳播者是自由變化的，它們分別用“*”和“°”表示，最終幾乎所有的節點都變成了用“+”表示的免疫者。然而，它們的演變規律存在明顯的差異，它們的現象如下。⑴無知者在前3天迅速減小并穩定在100人，這意味著幾乎每個節點都獲得了信息。⑵傳播者在第2.7天以前迅速達到峰值750人，說明一開始只受到了少數人的關注，隨后有眾多人在參與謠言的討論、轉發與交流，可以看出其傳播過程呈現出爆炸的特點，之后傳播者急速下降，到第4天時穩定在最小值0，表示這時人們對這個謠言關注度下降逐漸過渡到不再關注。⑶免疫者在2.7天后從0人迅速增加到900人，第4天后穩定在900，表示這時大家對這個謠言的真性產生懷疑或已對這個謠言失去興趣，對它的討論逐漸趨于平靜。

2.1.2 參數對謠言模型的影響

首先，參數μ1對謠言傳播中的傳播節點的影響如圖3所示，很容易看出，傳播節點的演變規律存在著明顯的差異。⑴當接觸率μ1越大，傳播的時間越早，傳播者峰值的數量也越大，信息傳播的持續時間也越短。⑵μ1的小幅增加將導致傳播節點的增加，這意味著μ1對于信息傳播是至關重要的。因此，為了抑制謠言信息的廣泛傳播，我們應該以各種方式有效地降低謠言信息的傳播率。

其次，參數μ2對謠言傳播中的傳播節點的影響如圖4所示。當受媒體影響的接觸率μ2 =0時，用“°”表示的傳播者迅速開始傳播謠言，很快，傳播者的人數達到了峰值1000，之后又迅速減少到0。當μ2的值相應地取0.01和0.018時，傳播速度和傳播的總人數都相應地減少。

因此，媒體對抑制謠言的傳播起著至關重要的作用，媒體可以有效地降低無知者的接觸率、對傳播者進行教育、提高媒體對疑議者的關注度等，能夠有效抑制謠言傳播。

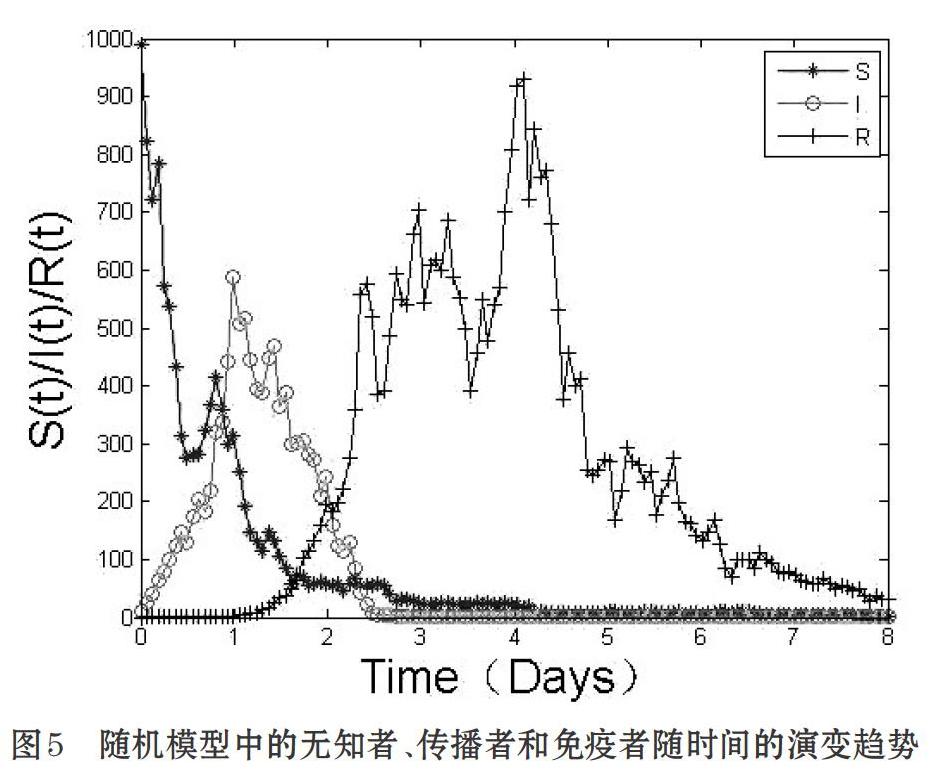
2.2 隨機微分方程的動態分析

除了增加一個方差δ=0.5外， 其它參數與上面確定性微分方程取相同的初值，實驗結果反映了個體模型的隨機性， 并顯示了受不確定性因素影響的結果，隨機微分方程揭示了謠言傳播的真實過程，這種方程更有實際意義。當方差δ取特別小的值時，圖形就變成了上面的確實性模型的演變趨勢圖，如圖5所示。

3 結論

本文研究了一類受媒體報道影響的確定性謠言傳播模型和隨機謠言傳播模型，并對確定性的謠言傳播模型進行了數學分析，得到了它的平衡點并討論了平衡點的穩定性。最后在數值模擬中表明這兩種模型能較好的反映謠言傳播的真實情況， 并研究了參數對確定性謠言模型的影響。

文中考慮的節點的傳播能力是相同的，這在現實中是有局限性的，有些影響力比較大的節點它的傳播能力相應也會大些，在以后的研究中爭取把這一點考慮進來。將隨機微分方程應用在謠言傳播模型處于初期階段，國內外相關的參考文獻也不多見，因此這種方法還未得到接受和認可，所以更談不上廣泛應用。

參考文獻（References）：

[1] Galam，S.Modeling rumors：The no plane pentagon french hoax case，Physica A.2003.320，571.

[2] Kimmel，A.J.Rumors and rumor control，J.Behavioral Finance.2004，5，134.

[3] Kosfeld，M.Rumours and markets，J.Mathematical Economics.2005.41，646.

[4] J.Kostka.Y.A.Oswald，R.Wattenhofer，Word of mouth： Rumor dissemination in social networks，Lecture Notes in Computer Science.058，2008：185–196

[5] Z.L. Zhang，Z.Q.Zhang，An interplay modal for rumour spreading and emergency development，Physica A.388，2009.4159–4166

[6] M.Kosfeld，Rumours and markets，Journal of Mathematical Economics.41，2005，646–664

[7] 蘭月新，突發事件網絡輿情謠言傳播規律模型及對策研究，情報科學，2012.56（9）：1334-1338

[8] 王超，楊旭穎，徐珂，馬建峰，基于SEIR的社交網絡信息傳播模型，電子學報，2014，42（11），2325-2330

[9] L Zhao，J Wang，Y Chen， Q Wang， J Cheng，SIHR rumor spreading model in social networks，Physica A Statistical Mechanics and Its Applications，2012.391（7）：2444-2453

[10] 徐璽翔，覃錫忠，洪麗平，傅云瑾， 復雜網絡上帶有傳播媒介的SICRS模型研究， 新疆大學學報（自然科學版），2015.32（4）：441-446

[11] Maki，～D.P.and M.～Thompson， Mathematical Models and Applications： With Emphasis on Social，Life，and Mangement Sciences，Prentice Hall.1973.