基于改進DNN-LSTM算法的車輛前方行人行為識別方法

(上海工程技術大學 機械與汽車工程學院，上海 201820)

0 引言

隨著汽車保有量的快速增加，交通事故數量和死亡人數一直處于較高水平，行人作為道路交通的主要參與者，保障行人安全是智能交通系統建設的重要目標之一。資料數據表明，在道路交通事故的人員傷亡中，行人橫穿道路發生的交通事故占較大比重。因此，實現對行人行為的有效檢測和正確識別，可保障交通環境中行人的安全，減少交通事故的發生率[1-2]。實現車輛前方行人行為的準確識別是汽車自動駕駛系統構建基本要求，對改善道路交通安全和交通質量具有重要的意義[3]。

車載攝像系統可對車輛前方的行人及道路狀況進行記錄，通過對記錄的視頻數據進行分析可識別出行人的行為動作[4]。根據視頻數據源不同可將行為識別方法劃分為三類：基于彩色視頻的行為識別、基于深度圖的行為識別、基于骨架節點的行為識別[5]。基于彩色視頻的行為識別方面，Feichtenhofer等人[6]提出了一種新的雙流網絡時空結構，將時間流和空間流產生的特征在時間和空間上進行3D融合識別視頻，但由于數據集中的干擾信息過多對識別精度產生了一定的影響。基于深度圖的行為識別方面，Vieira等人[7]在識別行為動作中，保留了時空單元之間的空間和時間的上下文信息，具有較高的靈活性。與前兩種方法相比，基于骨架節點的行為識別方法主要利用骨架的運動特征表示行為，具有更好的視圖不變性，減小了識別模型的復雜度和計算量[8]。Yang等人[9]利用人體關節點位置的差異性，提出了一種由特征信息構成骨架節點的表達方式，并作為特征描述符，利用樸素貝葉斯分類器進行行為識別。Boulbaba等人[10]使用中值濾波方法對骨架節點的軌跡進行平滑處理，并分別用最近鄰分類器和支持向量機對動作進行分類。Zhang等人[11]采用關節線距離作為輸入，以較少的訓練樣本數量獲得較好的識別結果。Zhu等人[12]提出了一種端到端完全連接的長短時記憶網絡用于基于骨架的行為識別。基于骨架節點的行為識別方法能夠有效的降低行為識別復雜程度，但由于其特征數據中包含干擾序列，致使該方法識別精度方面仍存在一定的改善空間。

綜上所述，本文以骨架節點為研究對象，建立了基于經驗模態分解(Empirical Modal Decomposition, EMD)的深度神經網絡-長短時記憶網絡(Deep Neural Network-Long Short Term Memory, DNN-LSTM)行為識別模型。該方法結合了經驗模態分解能夠平滑數據的優點，采用深度神經網絡對數據做特征分析，并利用長短時記憶網絡對獲取的行為特征做時序分析，從而實現對車輛前方行人行為的準備識別。

1 骨架節點特征提取

骨架節點特征提取是行人行為識別的關鍵技術之一。該方法首先以行人行為骨架節點為基礎，提取行人行為運動的關鍵參數，構建行人行為特征表征向量。勢能、加速度以及位置信息等特征在識別行人的行為動作方面具有很強的表述性。選取勢能、相對位置、加速度、角加速度作為表征參量描述行人行為，表征形式δi如公式(1)所示。

δi=[Eij,Pi,ai,γi]

(1)

式中，Eij為骨架節點的勢能變化特征；Pi為相鄰幀間同一關節點處的相對位置特征；ai為節點加速度特征；γi為關節點處角加速度特征。

為解決人與攝像機相對位置不同出現的誤差，利用相鄰幀間的勢能差來表示行人勢能的變化[13]，在行人的運動過程中，頭部相對肢體其他部位坐標變化較小，故選取頭部作為零勢能點,人體的勢能變化表示如公式(2)所示。

Eij=L(Pi,j-Pi,0)

(2)

式中，L為勢能參數，取9.8；Pi,j為第i幀中的第個骨架節點的像素；Pi,0為第i幀中零勢能點的像素。

不同運動情況下，相鄰兩幀間各骨架節點的相對位置變化量不同，其表達式如公式(3)所示。

Pi=Pi,j-Pi-1,j

(3)

式中，Pi-1,j為i-1幀第個骨架節點的像素。

行人動作可以看作一組骨架節點組成的剛體軌跡，不同的運動方式其速度與加速度會產生不同的變化，且變化差異較大。速度與加速度表達式如公式(4)所示。

(4)

式中，dt為相鄰兩幀之間的時間間隔；根據姿態估計算法性能，此處取為。

每個剛體的運動可看作是以剛體長度為半徑的圓周運動，都有對應的角速度和角加速度[14]。以膝蓋處的角速度和角加速度為例：設大腿處的向量為rm,小腿處的向量為rn，則關節角彎曲角度表達式如公式(5)所示。

(5)

式中，rm，rn分別為相鄰的兩向量；||為向量的模。

剛體的角速度及角加速度表達式如公式(6)所示。

(6)

式中，αi,j為當前幀膝蓋處的彎曲角度；αi-1,j為前一幀的膝蓋處的彎曲角度。

2 基于EMD的DNN-LSTM模型

針對提取的特征數據存在干擾信息以及需要考慮特征信息的時序性等問題，提出了基于EMD的DNN-LSTM網絡識別模型。該方法主要基于經驗模態分解方法對初始特征數據進行平滑處理，利用深度神經網絡對特征數據做非線性變換，并采用長短時記憶網絡分析連續幀間的變化規律。

2.1 模型原理

EMD[15]具有自適應特性，能夠根據數據自身的特征進行分解，把數據中包含大尺度的波動逐級分解開，用于處理非線性、非平穩性數據，并將各分量能量小于某一閾值的數據濾除達到數據去噪的目的。

其分解假設滿足兩個條件：在整個時序內，分量的局部極值點和零點的數目之差小于或相等1個；在任意時刻，局部極大值點形成的上包絡線和局部極小值點形成的下包絡線，均值為零。其分解步驟如圖1所示。

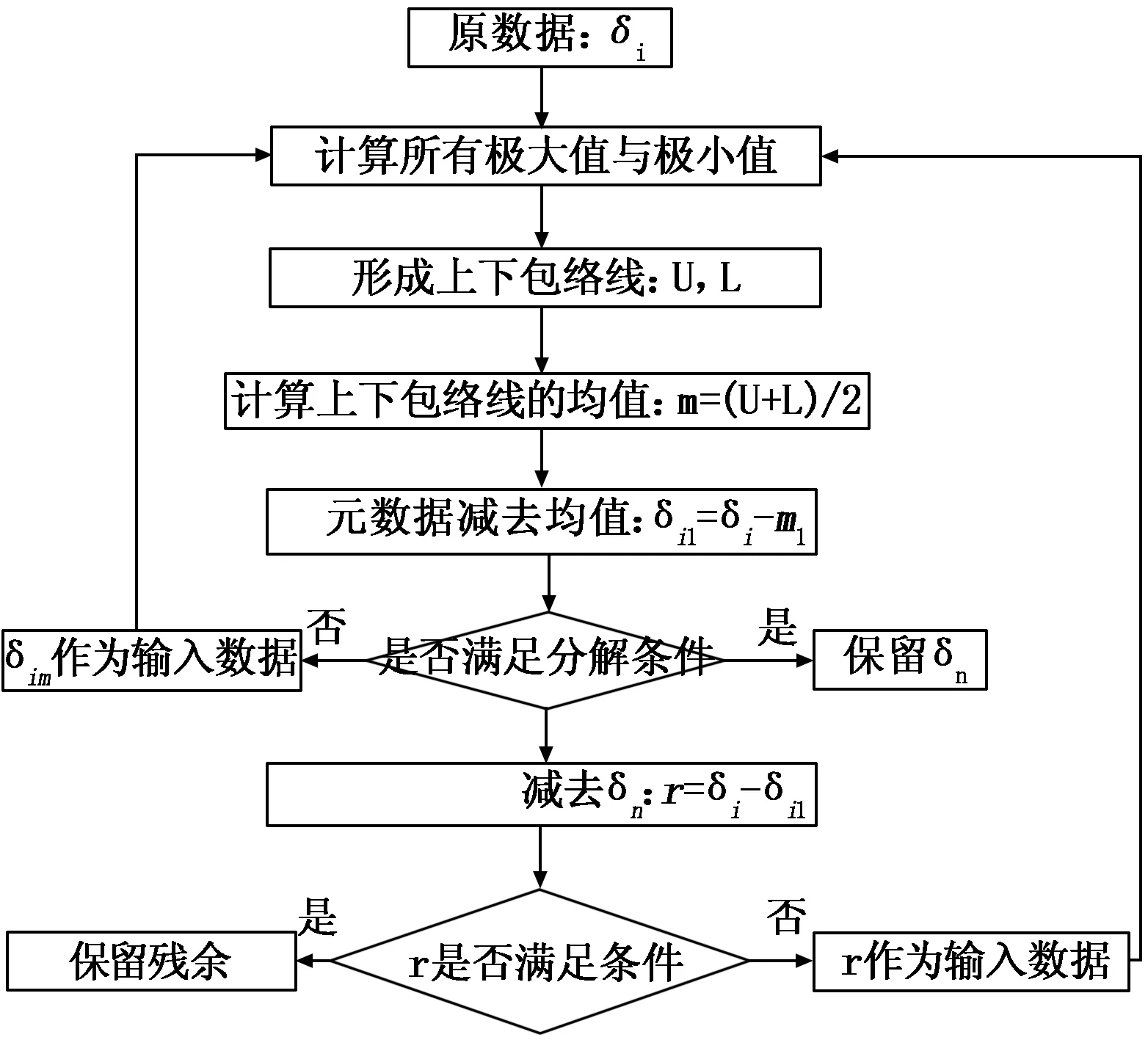
圖1 分解步驟

每個分量代表一個特征尺度的數據序列，分解過程即將原數據序列分解成各種不同特征波動序列的疊加。利用能量法根據提取的特征數據以及各分量的能量占比選擇合適的閾值M對數據進行處理，使特征數據更加平穩以利于后續識別階段的處理。

計算各分量的能量：

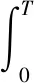
(7)

式中，T代表每個動作的總幀數。

計算各分量的能量占比：

(8)

式中，Ki為第i個信號IMF分量的能量比；I為信號分量的個數。

經過上述處理特征數據可以表示為：

(9)

式中，cj為原始信號的第j個分量；rn為原始信號的殘余分量。

考慮到模型的網絡性能和泛化能力，增加網絡層數可以提高精度但會使網絡復雜化，增加節點數會降低誤差，因此改進模型的深度神經網絡有4個隱含層，每個隱含層有32個神經元。但深度神經網絡對特征的處理在各時刻都是獨立的，循環神經網絡對特征的處理具有時序性，其神經元在當前時刻的輸入包括上一層神經元在該時刻的輸出和自身在前一時刻的輸出。長短時記憶網絡[16]在循環神經網絡的基礎上加入了門控機制，其細胞單元中包含輸入門、遺忘門和輸出門。

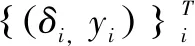
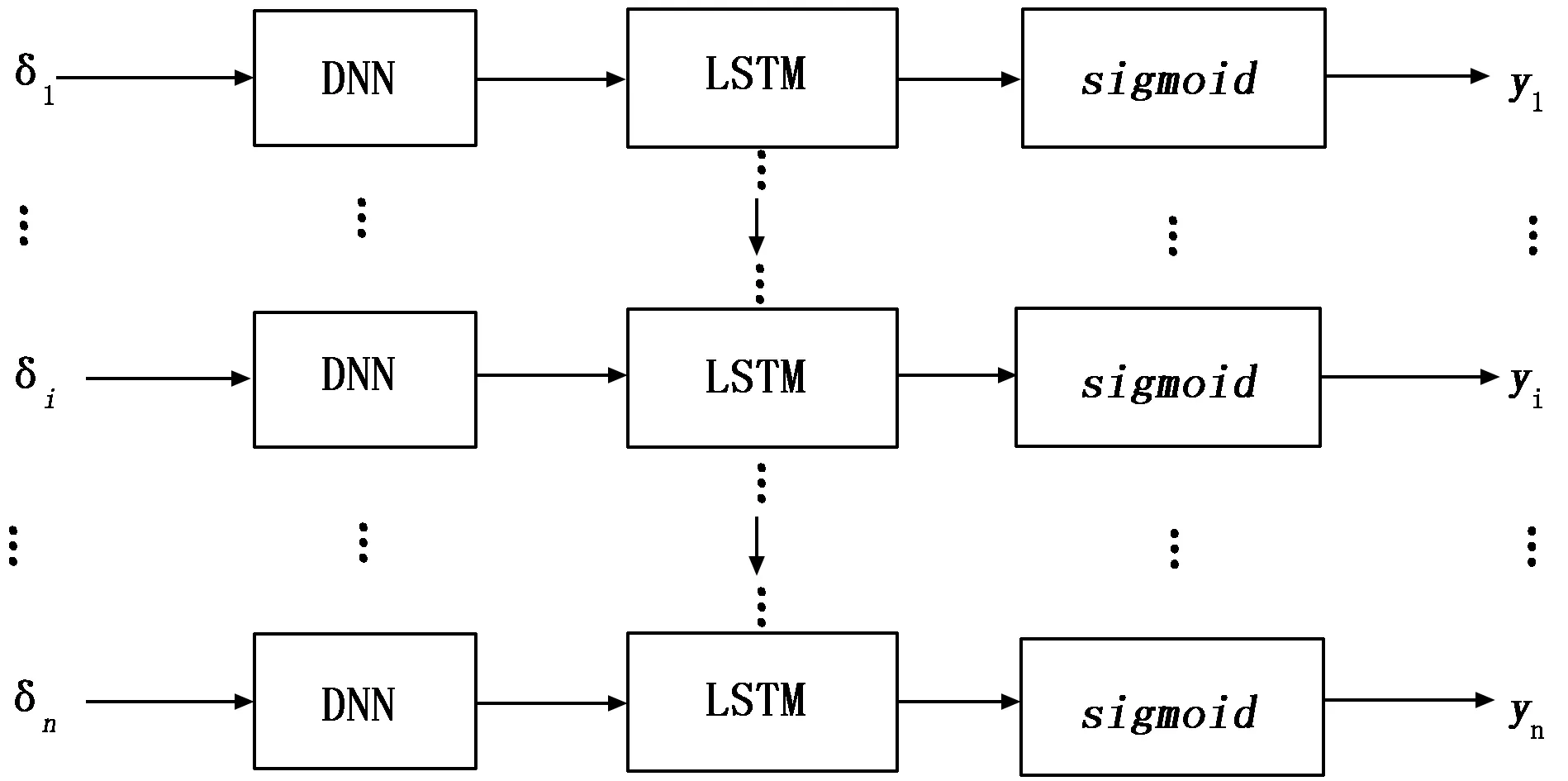
圖2 DNN-LSTM模型

當深度神經網絡具有l層網絡，其第l-1層共有m個神經元時,則第l層的第j個神經元的輸出表達式如公式(10)所示。

(10)

式中，tanh為神經元的激活函數；σ為sigmoid函數；ω為權重系數；δ表示當前層的輸入；b為偏置向量。

本文序列幀長度為N的特征序列δ=(δ1,δ2,…,δn)，標準LSTM單元按時間順序從t=1-n進行計算其計算公式如公式(11)～(16)所示。

遺忘門決定細胞單元中遺忘的信息，輸出一個0-1之間的數值輸入到輸入門，計算公式為：

(11)

式中，ht-1為上一個細胞的輸入；δ為DNN的輸出即LSTM當前細胞的輸入。

輸入門決定需要更新和丟棄的信息，分三步運算，σ決定更新的數據，tanh得到一個新候選值，決定加入到細胞狀態的比例，計算公式為：

(12)

(13)

(14)

輸出門是LSTM的最終輸出，先利用決定更新再與得到的新候選值相乘獲得最終輸出，計算公式為：

(15)

ht=ot*tanh(ct)

(16)

DNN輸出更明顯的特征向量后利用LSTM分析其時間序列特性[17]。對人體左右兩側分別進行特征提取，模型輸入層的節點數n=8，深度網絡層的節點數為32，激活函數為tanh函數，長短時記憶網絡層的神經元個數為64，激活函數為sigmoid函數，輸出層的節點數為1，激活函數為sigmoid函數。為解決過擬合問題，實現更有效地學習加入Dropout層，其比重設置為0.5。圖3為融合的神經網絡模型圖。

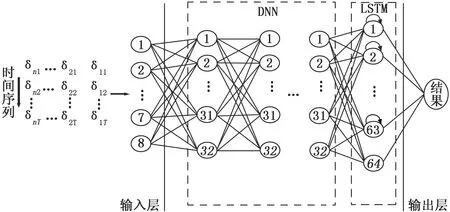
圖3 網絡模型圖

2.2 模型的訓練

有監督訓練在訓練過程中既有訓練數據又有訓練結果，訓練效果較好，因此采用有監督訓練，將處理好的特征輸入模型中，經過模型處理得出相應的識別結果。本文模型采用均方誤差函數(mean square error，MSE)作為損失函數，即將預測值與實際值作比較，利用損失函數計算識別結果與真實值之間的誤差。具體表達式如公式(17)所示。

(17)

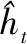
計算數據的損失梯度后，優化算法對損失進行優化，模型使用的優化算法是自適應學習率的Adam優化算法，利用梯度的一階矩估計和二階矩估計動態調整每個參數的學習率，一階矩估計的指數衰減率為0.9，二階矩估計的指數衰減率為0.999，使每一次迭代學習率都有明確的區間，參數較平穩，可較快預估結果。

3 實驗結果與分析

3.1 Weizmann數據集

Weizmann數據庫包含了10個動作，每個動作有9個不同的樣本，視頻的視角是固定的，背景中沒有嘈雜的環境。文中主要針對交通過程中行人的常見行為即行走和奔跑進行識別，將數據集中的剩余行為作為負樣本數據集進行處理。原始視頻數據經過前期預處理后分為訓練集和測試集兩部分。其中，訓練集用于建立模型和調整參數，測試集用于測試模型的識別精度，訓練過程中用2/3的動作數據作為訓練數據，1/3的動作數據作為測試數據。

3.2 預處理結果分析

對視頻中的動作利用一種自下而上的人體姿態估計算法[18]獲取人體各關鍵點的像素點，該算法檢測人體的十八個關鍵的骨架節點，是特征提取的基礎。圖4為對實際場景中行人檢測的序列圖。

圖4 行人運動序列圖

圖5和圖6分別為跑步和行走時的足部軌跡圖。從圖5中的前14幀以及15幀到30幀，可以看出行人的運動軌跡呈周期性變化，從圖6中可以看出左右腳的位置呈互補關系，證明檢測算法的準確性和可靠性較高。對某一幀骨架節點像素值全為零的情況，利用前兩幀的數據變化規律進行補缺的方法填補特征數據。

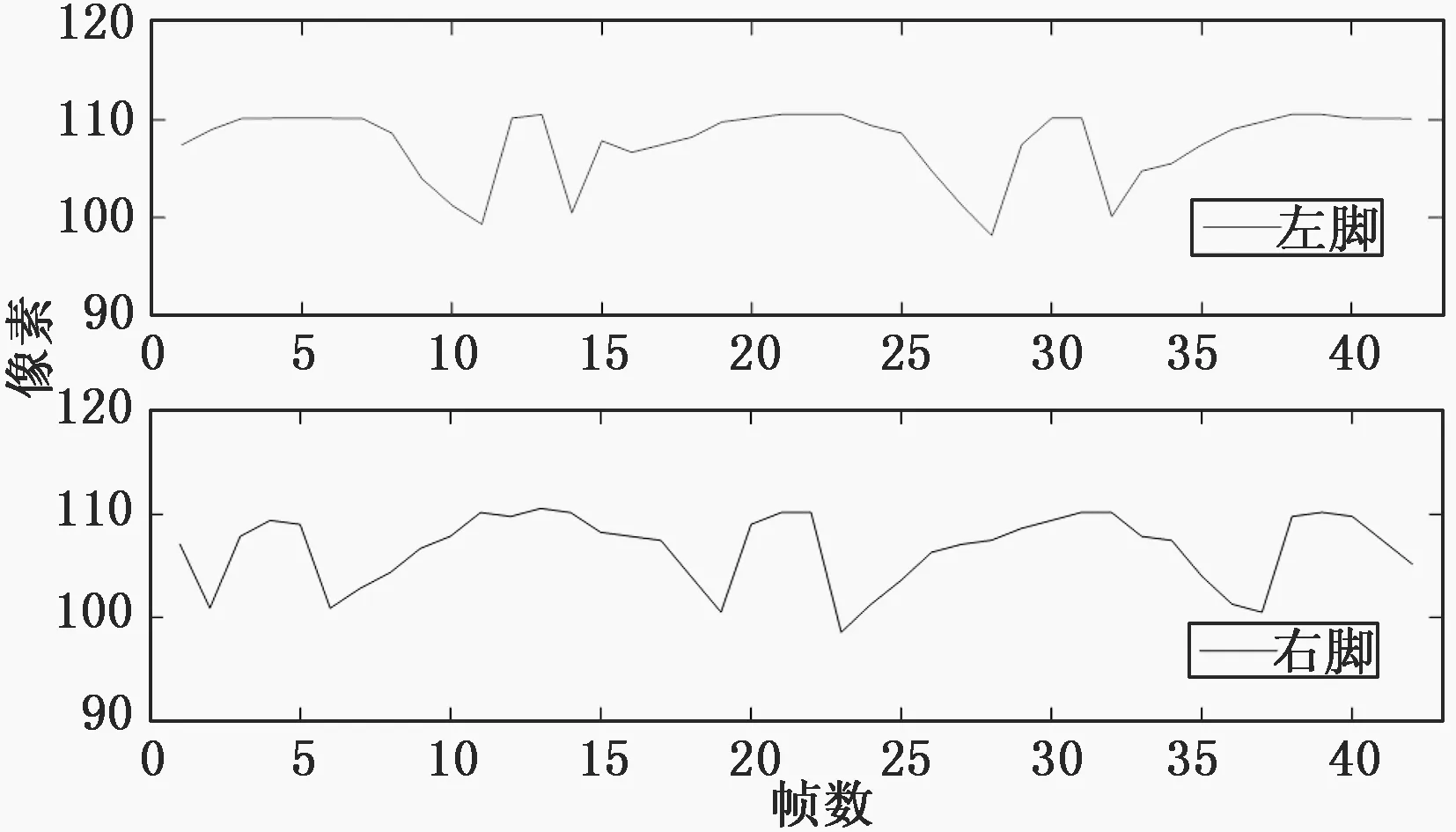
圖5 跑步時足部軌跡圖

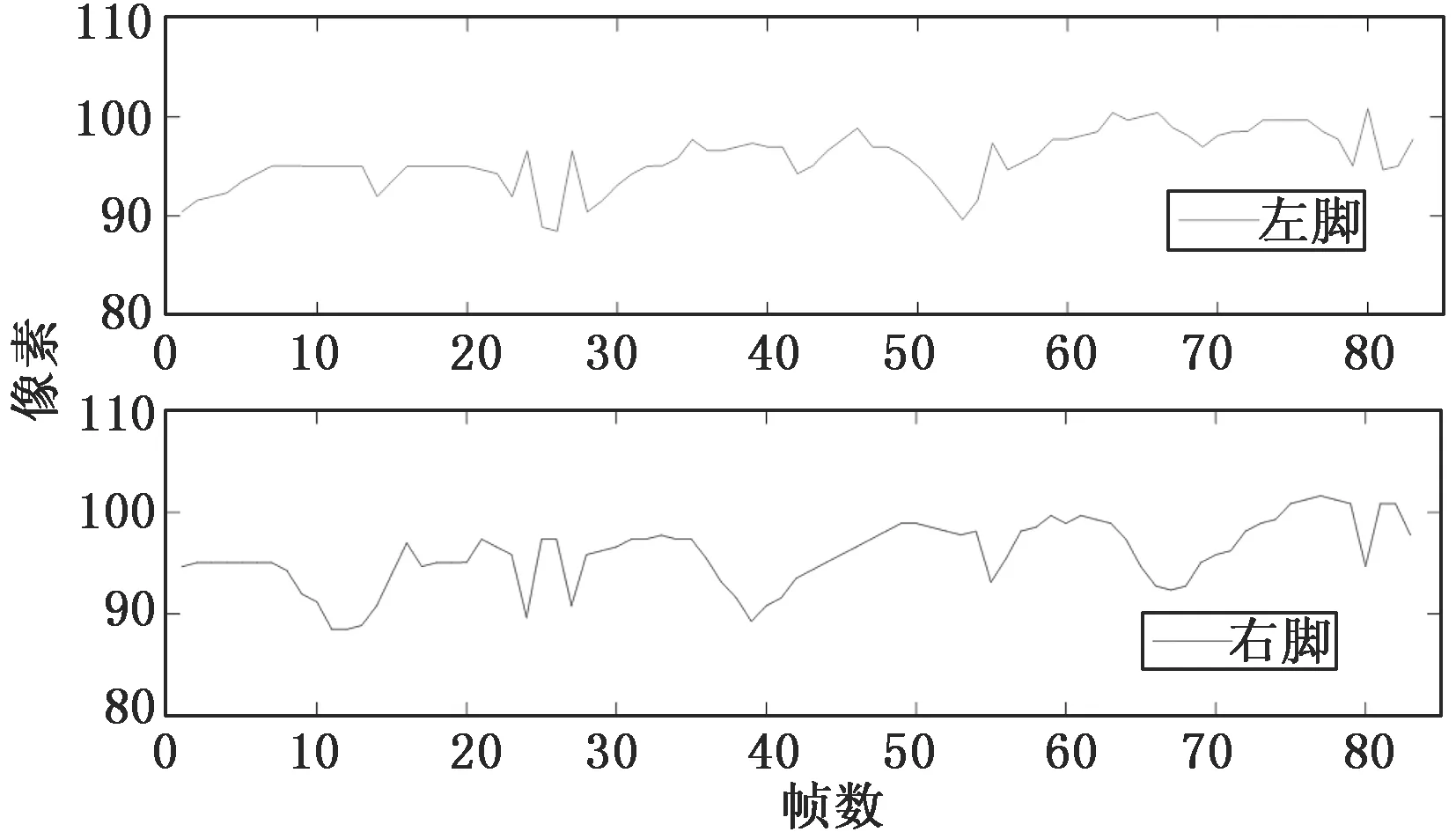
圖6 行走時足部軌跡圖

3.3 實驗結果分析

為了校驗基于改進DNN-LSTM算法的車輛前方行人行為識別模型的有效性，采用常用的傳統DNN模型、LSTM模型以及DNN-LSTM模型作為對比模型。對比試驗采用相同的試驗數據作為輸入，對比結果如圖7至圖8及表1所示。圖7為各模型在整個訓練過程中隨著訓練迭代次數增加的損失變化圖，圖8為精度變化圖，為了能更清晰直觀的比較各個模型的損失與精度之間的差異，從迭代30次后進行對比。

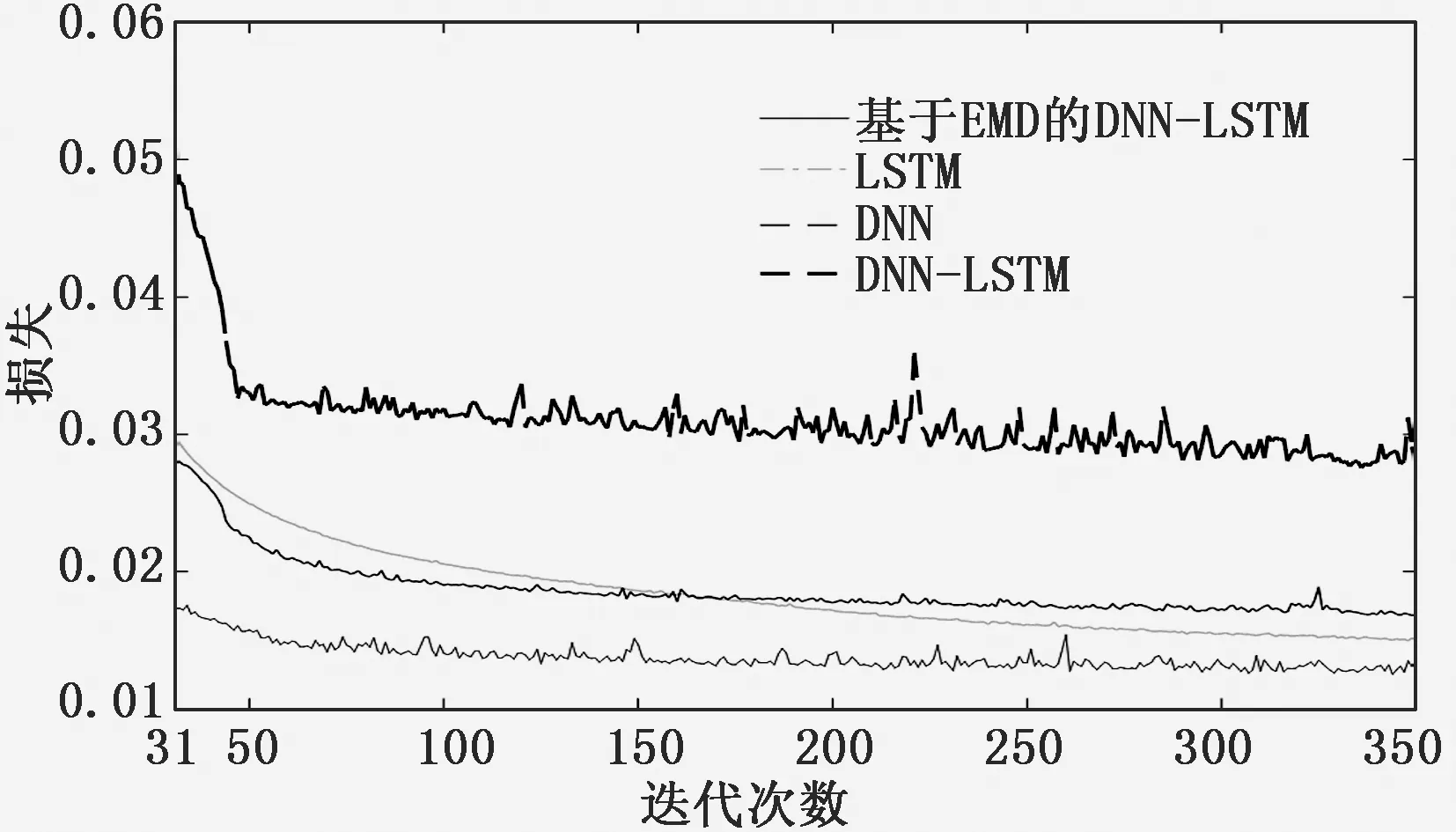
圖7 各模型訓練損失圖

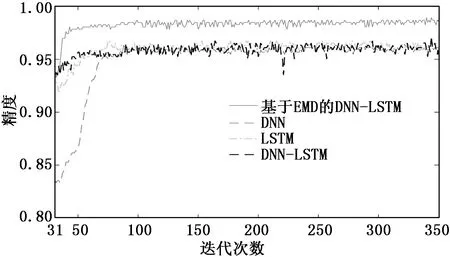
圖8 各模型精度圖

從圖7中可以看出，在訓練過程中基于改進DNN-LSTM算法的網絡模型在迭代150次左右已趨向穩定，趨于穩定的速度明顯快于其他模型，且其損失值比其他3種模型更小。未經平滑處理的特征數據在訓練過程中的損失較大，證明特征數據平滑處理的必要性；其余3種模型均用預處理后的特征數據做為訓練模型的輸入，損失下降過程中波動較小，且損失值與未經預處理的模型相比下降0.01左右。

圖8可以看出，隨著迭代次數增加精度均呈增加的趨勢，在迭代次數達到100次左右時精度趨于穩定。傳統DNN模型在迭代過程中精度上升最慢；未經EMD處理的模型的精度波動最大，平穩性較差；改進DNN-LSTM算法的網絡模型識別精度明顯高于其他3種模型，且訓練后期穩定性較好。

表1為對Weizmann數據集進行行為識別的準確率與其他模型的識別準確率對比表，從表中可以看出識別準確率由高到低依次為：改進自行車的DNN-LSTM、DNN-LSTM、LSTM、DNN。在特征提取階段簡化了識別模型的輸入，減少了模型輸入的參數量，模型的計算效率有所提高。改進DNN-LSTM算法的網絡模型識別準確率要高于其他3種類型，主要原因是對特征進行了平滑處理以及用LSTM網絡進行時間序列分析；并證明改進DNN-LSTM算法模型可提高行為識別的準確率。

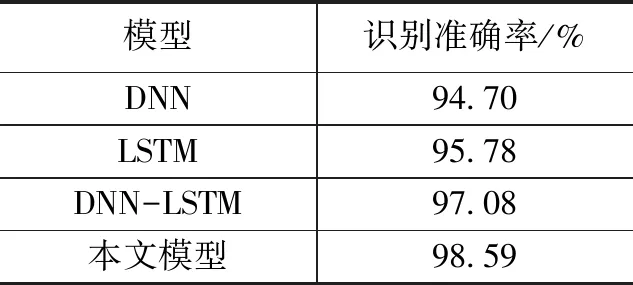
表1 與其他模型識別準確率對比表

為證明模型的可行性，采用KTH數據集對模型進一步訓練和測試，KTH數據集由25個人在4個不同場景下進行的6類動作組成，共有2391個視頻樣本。視頻樣本的外在環境變化包括尺度變化、衣著變化和光照變化，將慢跑與跑步視頻作為跑步數據集，行走作為行走數據集，剩余行為作為其他負樣本數據集，數據集的前期處理與Weizmann數據集相同，最終的識別部分依然用數據集中2/3的動作數據作為訓練數據，1/3的動作數據作為測試數據。識別精度達到98%，證明本模型在KTH數據集上也同樣適用。

4 結論

本文提出了一種基于EMD的DNN-LSTM的深度學習模型進行行為識別。提取關鍵骨架節點的特征向量后利用EMD降低特征數據的不平穩性，最后用DNN-LSTM模型實現行為識別，模型表現出不錯的識別效果。

(1)為評估新模型的性能，分別在DNN、LSTM、DNN-LSTM、改進的DNN-LSTM四個模型上利用Weizmann數據集進行訓練與測試，結果表明新模型的測試識別率達到98.59%，高于其他3個模型。

(2)新模型在KTH數據集的測試精度達到98%，證明該模型適用于兩種數據集，具有較高的可行性。由于實驗中采用的數據集背景比較單一，且均為單人動作，與現實場景有所偏差，未來將對復雜環境下的多人場景進行行人的行為識別。