基于位置反解算法的并聯機器人坐標變換方法

(河南工程學院, 鄭州 451191)

0 引言

目前，工業生產自動化水平不斷提高，各個行業生產機器人正在快速發展，比如汽車加工、物流倉儲、食品飲料、機械制造等領域機器換人的速度正在逐漸提升，未來工業機器人、服務機器人甚至特種機器人都將成為我們生產生活中不可或缺的設備。工業機器人包括并聯機器人和串聯機器人，并聯機器人通過并聯方式驅動,由兩個以上獨立的運動鏈相互連接,無累積誤差及精度較高是并聯機器人的突出特點，所以，在工業生產、機械制造等領域獲得了廣泛的應用。同時，并聯機器人的驅動裝置可以固定在定平臺上，從而使得并聯機器人的運動部分速度比較高、重量比較輕、動態響應比較好，所以，在活動工作空間較小，進行精細及高剛度、大載荷加工的工件加工領域內應用較廣，發展較快。

對于工業機器人工作的場合,通常需要在線獲取機器人的實時位置，而串聯機器人求解正解較為方便，而求解反解則非常困難。因為并聯機器人的并聯機構是對稱的,所以各向同性較好,可以通過空間變換進行位姿反解從而求取并聯機器人的桿長值。

1 系統結構及原理

一個完整的并聯機器人系統包括外部傳感器、執行結構、控制器等，外部傳感器用來檢測并聯機器人所處的工作環境和工作狀態，執行結構用來執行具體的操作，控制器用來判斷和發出指令，當對機器人發出指令時，需要將其編寫成計算機所能執行的機器語言載入到機器人的控制器中。六自由度并聯機器人的控制系統核心結構為：嵌入式系統、步進電機及其驅動器及控制器等，同時還包括電源適配、控制柜、導軌、電磁閥、人機交互界面等幾部分，同時，在嵌入式計算機內安裝可以控制機器人工作的軟件和運動控制卡。

機器人的控制技術是決定機器人技術發展的關鍵因素，機器人的控制系統是決定并聯機器人控制功能和控制原理的首要因素，它的主要作用是控制并聯機器人在指定的空間內的運動位置、運動軌跡、加工操作順序、加工執行方式等。其包括組織層和協調層，組織層負責軌跡規劃和任務空間下完成任務的位姿描述，協調層包括反解計算各個關節值和關節空間的軌跡規劃等，在機器人控制器中有機器人自身的控制模型、環境模型，它會根據具體工作環境和工作狀態選擇一種適合當前情況的控制算法和任務調度規則，信號通過控制器被發送至執行機構，即電機驅動器等一系列裝置，期間也在不間斷地受到外部傳感器的監測，同時，將檢測結果傳送到控制器。最終執行層的狀態則需要外部傳感器的檢測配合，環境模型的建立也需要外部傳感器獲取的外部環境信息，到此為止，一個完整的閉環并聯機器人系統就形成了。

并聯機器人的驅動系統的作用是提供各個可運動部位所需要的原動力。常見的驅動系統分為電力驅動、氣壓驅動和液壓驅動，也可以是三者結合起來的綜合驅動系統。從輸出功率、響應速度、控制性能、安全性能等多方面的考慮和比較，并且由于該機器人在室內并且應用于高精度的點位以及連續軌跡控制系統中，因而采用電力驅動作為該機器人的主要驅動方式。

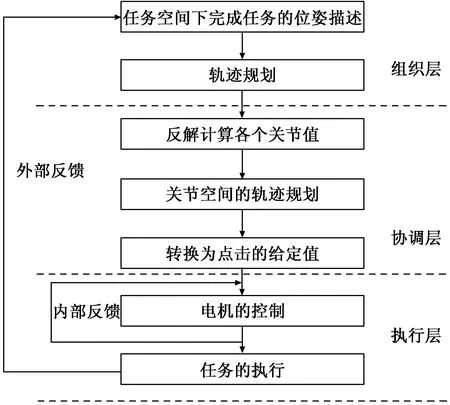
圖1 工作原理

2 算法分析

并聯機器人的反解算法：

本并聯機器人設計采用上下兩個平臺構成，下面的平臺是靜止的，為靜平臺，在其上建立的坐標系我們把它叫做靜坐標系。上面的平臺是可以移動的，為動平臺，在其上建立的坐標系我們把它叫做動坐標系。b1至b6為上平臺的6個坐標點，分別對應上平臺的6個絞點，6個絞點之間的位置是根據運動情況變化的；B1至B6為下平臺的6個坐標點，分別對應下平臺的6個絞點，6個絞點之間的位置是固定不變的。

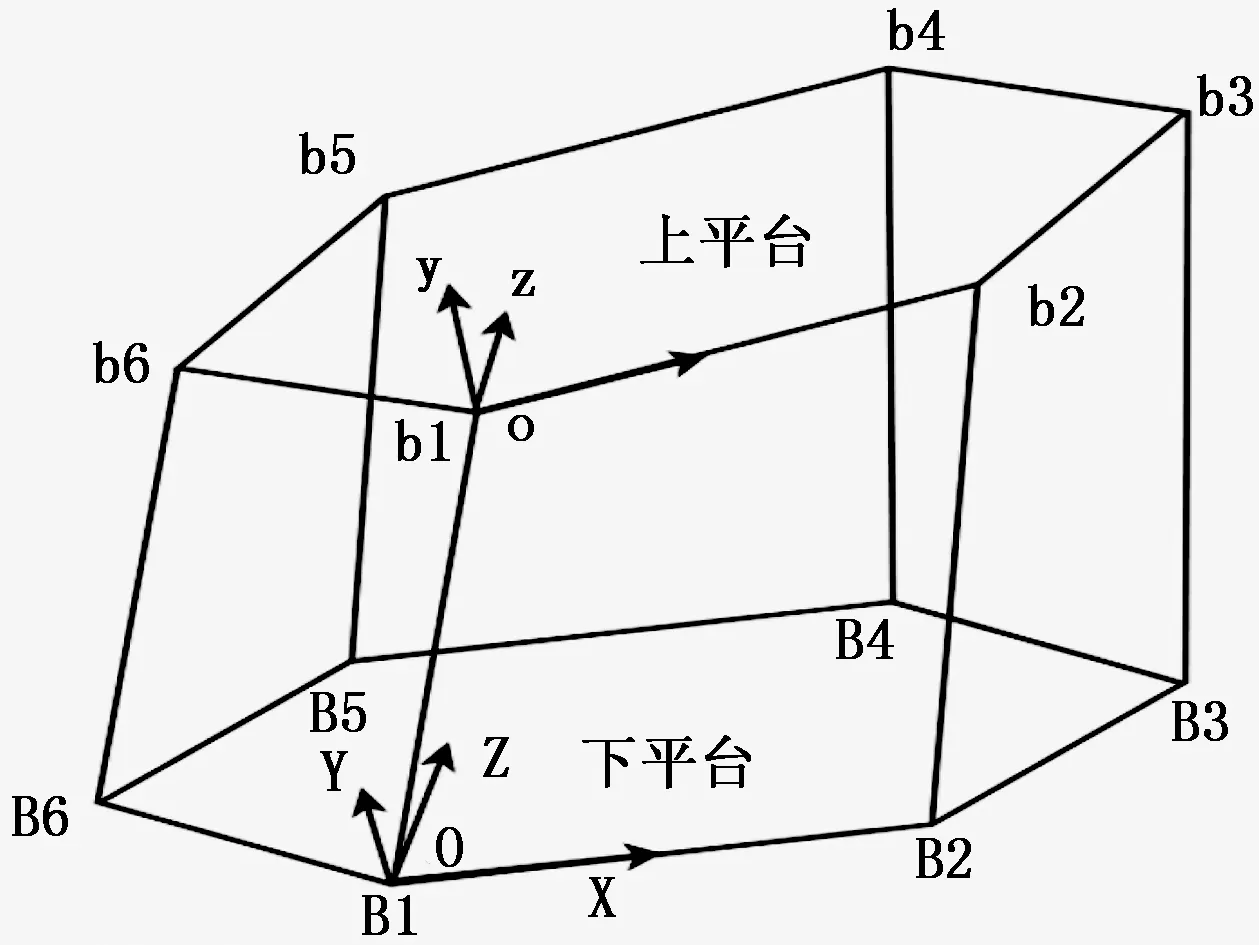
圖2 6自由度并聯機器人空間結構圖

具體分析如下：在動坐標系o-xyz建立在上面的動平臺，定坐標系0-XYZ建立在下面的定平臺上。經過分析后得知動平臺運動的實質就是空間的變換與定平臺之間的關系。可以用數學表達式表示兩者之間的變換關系。靜坐標系中的R可以用動作標系中的任意一個向量R′通過坐標變換求得。其變換公式為：

R=TR′+P

(1)

式子中：T為上平臺姿勢的方向余弦矩陣；P是在動平臺上選的參考點，它是動坐標系的原點相對于靜坐標系的位置矢量值。

(2)

上述式子中：T矩陣是建立在動坐標系里的x，y和z在下平臺靜定坐標系中的方向余弦矩陣，α、β、γ三個參數為以在下面的靜平臺上建立的精坐標系為基準，在上面的動平臺上建立的動坐標系分別沿x、y、z三個軸旋轉所轉過的角度。

P=[XP,YP,ZP]T

(3)

當并聯機器人各個部分結構及尺寸確定后，通過空間幾何變換，就可以計算出上下兩個平臺各鉸鏈點(bi，Bi，i=1，2，…，6)在各自坐標系個的坐標值據此可以計算出電動驅動桿的長度L。

其公式為：

li=bi-Bii=1，2，3，…6

(4)

(5)

從而得到機構的位置反解計算方程：

(6)

(6)式有6個方程，共有6個未知數，通過獲取并聯機器人上下兩個平臺的位置和姿態，就可以利用上式求出6個驅動桿的位移。這就是所研究的并聯機器人的位置反解問題通過靜平臺與動平臺之間的坐標變換構造空間矩陣進行計算的結果公式。

為了更好地表示空間內靜平臺所作的平移變換和旋轉變換，也可以借助齊次坐標來表示所在點的空間位置，各點在空間的轉動和平移等位置，可以通過齊次變換矩陣來計算表示。可以假定空間某點M的笛卡爾坐標為M(x、y、z)，然后用一個四維列向量T[xyz1]表示M點的齊次坐標。這種表示方法有兩個優點，使用齊次變換矩陣不僅可以規定表示坐標點的位置，還可以用來規定表示矢量的方向，即當第4個元素為1時，代表該變換矩陣表示坐標點的位置，而第4個元素為0時，代表該變換矩陣表示坐標點的方向。

反解算法的步驟如下：

1)查閱機器人的結構資料，獲得并聯機器人的原始數據。

2)建立并聯機器人的動靜兩個坐標系并確定其原點。

3)求出動坐標系的原點以及各個鉸點相對于靜坐標系中的位置矢量。

4)跟據機器人的各個部位結構尺寸求出初始狀態下各個桿長。

5)給出變化后的靜平面的各個鉸點相對于原靜平面的坐標。

6)再次求出動坐標系各個鉸點相對于靜坐標系中的位置矢量。

7)計算出此時電動驅動桿的長度L。

3 算法驗證

并聯機器人的正解問題就是已知驅動桿變化的長度變化量，求動平面所在空間的位置坐標，求解并聯機器人的正解會出現一個復雜的多解問題，當然，我們可以通過使用差分算法進行求解，不過，這相對于反解算法問題進行數學問題的換算分析，這種方法則要復雜的多。

為了驗證該反解算法的可行性和有效性，文中通過MATLAB進行了仿真驗證。先建立上下兩個平臺的動坐標系和靜坐標系，并求取上平臺各絞點相對于下平臺的坐標值，然后再根據并聯機器人的資料計算求解初始狀態的各個驅動竿的長度，給出靜平面的目的坐標值，重新求出動平面各個絞點相對于靜坐標系中的位置矢量值，最后根據上下兩個平面各絞點坐標求取得到驅動竿的長度。

部分源程序如下：

t=0:0.1:2;

y1=-4.48*t.^3+13.43*t.^2+38.74;

figure(1)

其次，要綜合考慮上下游營改增政策的實行狀況，對定價和收款的方法進行合理的調整。尤其是下游不動產企業，在其執行營改增政策以后，要對雙方的納稅需求進行統籌分析，提前籌劃，有效節省稅制變動成本的支出。

plot(y1)

y2=-4.98*t.^3+14.93*t.^2+42.90;

figure(2)

plot(y2)

y3=-0.98*t.^3-2.93*t.^2-2.81;

figure(3)

plot(y3)

y4=0.7*t.^3-2.10*t.^2-1.12;

figure(4)

plot(y4)

y5=-3.75*t.^3+11.24*t.^2+32.84;

figure(5)

plot(y5)

y6=-3*t.^3+9*t.^2+26.95;

figure(6)

plot(y6)

算法驗證所用并聯機器人的結構尺寸參數設置如下：

并聯機器人的自由度：6

驅動桿的長度：l=223 mm

上平臺外接圓的直徑：R=129.74 mm

下平臺外接圓的直徑：r=65.5 mm

各驅動桿的行程：100 mm

驅動元件的方向：Z向

驅動元件的最小伸長量：158.896 6 mm

驅動元件的最大伸長量：258.896 6 mm

所選6自由度并聯機器人空間坐標及并聯機器人的驅動竿的初始長度設置如表1所示。

選擇確定上下兩個平臺各絞點坐標及初始狀態下的驅動桿的長度為212.57 mm，在實際運行過程中，由于并聯機器人本身機械結構的原因bi點(動平臺的各個鉸點)的實際運行軌道為僅沿Z軸平行移動，而X軸與Y軸坐標均不會發生改變。因此上面動平臺上鉸點的各個坐標的z軸變化量就是驅動關節滑塊的移動距離208.897 mm。

經對對反解算法進行仿真計算，可以得到上平臺各個絞點變換后的坐標值，并且，當靜平面的目標值為(0，0，50)時，得到各個驅動桿的長度為163.61 mm，變化量為48.96 mm；當靜平面的目標值為(0，0，-20)時，得到各個驅動桿的長度為232.25 mm，變化量為19.68 mm；并聯機器人運動后的結果表明：對于各種不同結構的并聯機器人，只要根據其結構分析建立其空間坐標系我們就能對其進行反解解算，這種并聯機器人坐標求解方法具有普遍性，輸入目的坐標值即可獲得上平面各鉸點坐標及驅動桿長的變化量。

4 小結

并聯機器人在工業生產、精密加工、汽車電子、航空航天等領域的應用隨著智能制造技術的深入發展會日益增加，而對并聯機器人的控制方法也必定會不斷革新。通過本次對并聯機器人的工作原理和機械結構的設置，及其位置變換解的反解算法的研究，對其位置反解定位方法進行了介紹和驗證,驗證結果表明,與正解算法相比基于位置反解算法的并聯機器人坐標變換方法更加簡潔有效,具有更大的應用價值和應用潛力，經過簡單的計算即可獲得各個機器桿的變化量,并聯機器人結構中沒有驅動器的累積誤差，因此使得它們具有很高的精度。此外大多數的并聯機器人可以保證基座驅動器的密封性，在較為潮濕、有輻射、高溫甚至在太空等惡劣的環境下仍可保持良好的性能,應用環境也更為廣泛。

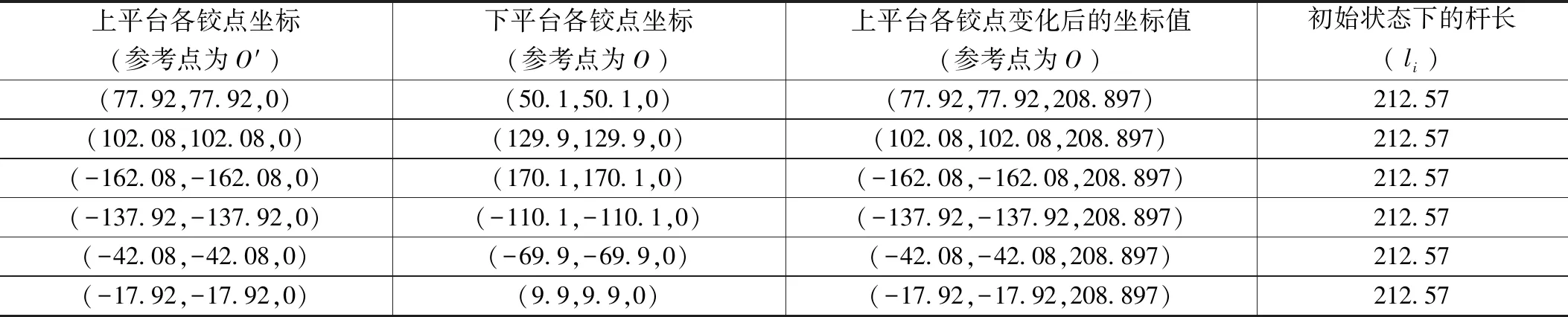
表1 所選機器人初始桿長與坐標

注：以上坐標由并聯機器人的機械結構以及其初始狀態所決定。

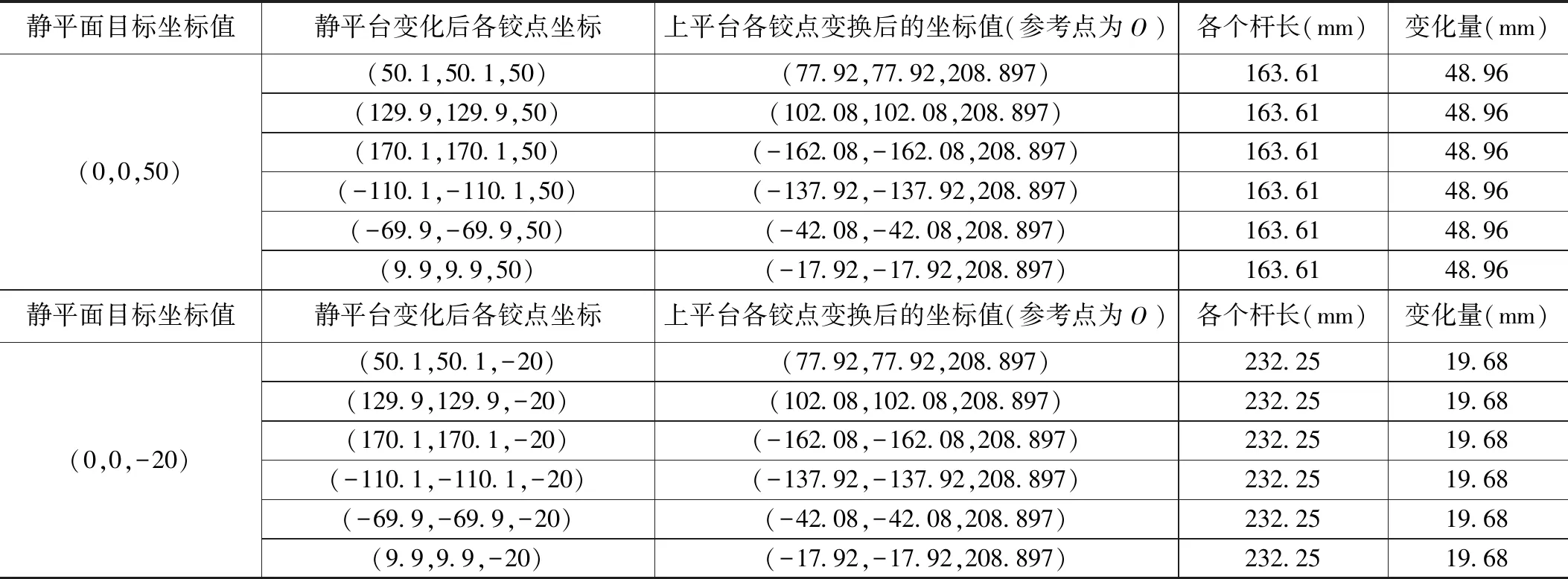
表2 運動后的桿長及其變化量

注：以上變化起始點均為(0，0，0)。