PCE方法在空間實驗室軌道預(yù)報誤差分析中的應(yīng)用

歐陽琦，陳 明，李翠蘭，李 勰

(北京航天飛行控制中心，北京 100094)

0 引 言

隨著人類航天活動的日益頻繁，在軌空間目標數(shù)量不斷增加，對航天器的在軌管理以及后續(xù)的航天任務(wù)帶來了新的挑戰(zhàn)。航天器在軌運行管理期間，一方面需要協(xié)調(diào)測控資源對其進行跟蹤，另一方面還需要計算與其他空間目標的相對位置關(guān)系以進行有效地碰撞預(yù)警，因此，對航天器軌道預(yù)報的誤差進行分析至關(guān)重要。

航天器軌道預(yù)報是根據(jù)航天器初始時刻狀態(tài)進行動力學(xué)積分的過程。在這個過程中，由于知識缺乏、航天器所處的環(huán)境客觀可變，航天器初始時刻的狀態(tài)、動力學(xué)模型等都存在不確定性。對這些不確定性的度量以及其在軌道預(yù)報中傳播規(guī)律的研究是軌道預(yù)報誤差分析的關(guān)鍵。傳統(tǒng)的軌道預(yù)報誤差分析方法大都基于線性模型或蒙特卡洛仿真方法(Monte Carlo simulation, MCS)[1-2]。基于線性模型的方法也稱為線性傳播方法，這種方法計算效率高，然而對于非線性程度較強的系統(tǒng)以及中長期預(yù)報來說，精度較差；MCS方法精度較高，然而需要大量的樣本點才能計算得到高精度的計算結(jié)果，計算效率低。為克服上述方法的不足，近年來許多學(xué)者對軌道動力學(xué)中非線性不確定性傳播方法進行了研究[3-4]。多項式混沌展開法(Polynomial chaos expansion，PCE)起源于Wiener和Ito對于無序運動的數(shù)學(xué)描述，屬于隨機展開法中的一種，實質(zhì)上是對隨機變量構(gòu)建一個具有隨機性的近似模型[5]。該方法在結(jié)構(gòu)設(shè)計[6-7]、流體力學(xué)[8-9]等領(lǐng)域得到了廣泛的應(yīng)用。近年來，Jones等[10]將PCE方法應(yīng)用于軌道預(yù)報誤差分析之中，并對太陽同步軌道和閃電軌道的軌道誤差傳播進行了測試，驗證了該方法的有效性。

2016年9月15日，天宮二號空間實驗室及其搭載的空間應(yīng)用系統(tǒng)發(fā)射升空，對我國未來空間站建設(shè)的關(guān)鍵技術(shù)進行了驗證[11-12]。空間站質(zhì)量體積大、空間構(gòu)型復(fù)雜、組合體運行模式多變，對其在軌管理技術(shù)難度較大。本文將PCE方法應(yīng)用于空間實驗室軌道預(yù)報的誤差分析，為我國未來空間站的建設(shè)和在軌管理提供有益參考。

1 PCE方法簡介

本節(jié)對PCE方法進行簡要介紹，包括PCE模型、PCE方法的應(yīng)用形式、PCE系數(shù)的求解以及隨機變量統(tǒng)計信息的求解幾個部分[13]。

1.1 PCE模型

采用PCE，任意分布的隨機變量u可以展開為：

(1)

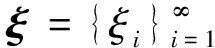
(2)

PCE方法均方收斂。當(dāng)p≠q時，Γp與Γq正交，極大簡化了均值及方差等信息的計算過程。為了實際應(yīng)用的需要，通常截取到一定階數(shù)。將ξ的個數(shù)定義為PCE的維數(shù)，Γ的個數(shù)即PCE的階數(shù)，則d維p階PCE模型涉及的系數(shù)個數(shù)P為：

(3)

在實際運用中，通常采用更加簡潔的形式：

(4)

式中：bi與系數(shù)ai1,…,aip以及Ψi(ξ)與函數(shù)Γp(ξi1,…,ξip)之間是一一對應(yīng)關(guān)系。

1.2 PCE方法的應(yīng)用形式

PCE方法一般有侵入式與非侵入式兩種應(yīng)用形式。侵入式方法將系統(tǒng)模型中的不確定性變量進行隨機展開，并將其代入系統(tǒng)分析模型中；非侵入式方法將系統(tǒng)模型作為黑箱處理，直接對系統(tǒng)的輸出進行隨機展開，建立系統(tǒng)輸出對不確定性輸入變量的顯式表達式。對于軌道預(yù)報來說，若航天器初始位置速度存在不確定性，侵入式方法將位置速度近似成一系列隨機變量的展開形式，軌道動力學(xué)方程也需要修改成一系列隨機變量的方程；非侵入式方法則將軌道預(yù)報過程看作一個黑箱，不對軌道動力學(xué)方程進行修改，通過生成一系列樣本點來構(gòu)建預(yù)報時刻的航天器位置速度與初始時刻航天器位置速度的不確定性傳播關(guān)系。由于非侵入式方法無需對軌道動力學(xué)方程進行修改，一方面在工程應(yīng)用中不需要修改現(xiàn)有代碼，另一方面也避免了方法研究與實際對象的耦合關(guān)聯(lián)，與侵入式方式相比應(yīng)用范圍更廣，因此本文采用非侵入式PCE方法。

1.3 PCE系數(shù)的求解

對于非侵入式PCE方法，其系數(shù)求解時需要生成一系列樣本點，計算每個樣本點處的輸出變量值，從而構(gòu)建待定系數(shù)的求解方程。常用的樣本點生成方法有蒙特卡洛仿真法、正交試驗設(shè)計法(Orthogonal array sampling, OAS)和拉丁超立方法(Latin hypercube design, LHD)等[13]。其中，拉丁超立方法是一種分層抽樣法，可以生成分布較為均勻的樣本點，通過較少的抽樣次數(shù)就可以獲得較好的精度。本文采用拉丁超立方法生成樣本點。給定一組樣本及其對應(yīng)輸出變量值，可以計算PCE模型中的待定系數(shù)。目前發(fā)展了多種求解待定系數(shù)的方法[14]，其中Galerkin投影法和回歸法是兩種主要求解方法。Galerkin投影法通過利用多項式的正交性，進行內(nèi)積操作將函數(shù)分別投影到每個基函數(shù)項上，得到相應(yīng)系數(shù)。回歸法則是通過最小化某些樣本點上PCE預(yù)測響應(yīng)值和真實響應(yīng)值間的誤差平方和來求解PCE中的待定系數(shù)。本文采用回歸法求解PCE中的待定系數(shù)。具體步驟如下：

(1)隨機選取N個樣本點{ξ1,ξ2，…,ξn};

(2)計算樣本點對應(yīng)的響應(yīng)值{y1,y2…，yn}，其中，yi=u(ξi),i=1,…,n，從而構(gòu)建如下方程:

Ab=Y

(5)

式中：

1.4 統(tǒng)計信息的求解

當(dāng)PCE模型中的系數(shù)確定后，便可以方便快速地得到隨機變量的均值、方差等統(tǒng)計信息，如下：

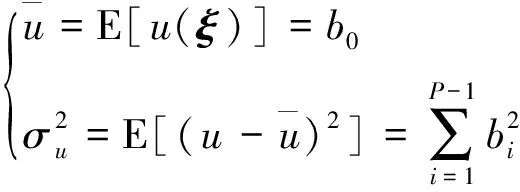
(6)

另外，若要計算隨機變量的高階矩或概率分布，可以通過蒙特卡洛仿真方法隨機產(chǎn)生一系列樣本點并計算PCE模型輸出值，進而計算相應(yīng)的統(tǒng)計信息。

2 基于二體模型的軌道預(yù)報誤差傳播

2.1 問題描述

本節(jié)將PCE方法應(yīng)用于空間實驗室軌道預(yù)報誤差分析。PCE模型精度主要受PCE模型階數(shù)、預(yù)報時長以及樣本點的數(shù)目這幾個因素的影響，因此本節(jié)針對以上因素展開討論。考慮工程應(yīng)用的需要，本節(jié)考察預(yù)報時長為1天和7天。表1給出了歷元時刻2018- 03-17T08∶00∶00.000的初始位置和速度值。假設(shè)J2000坐標系下的初始位置和速度存在誤差，標準差分別為10 m和1 m/s。為簡化模型，本節(jié)的軌道預(yù)報模型基于二體假設(shè)。

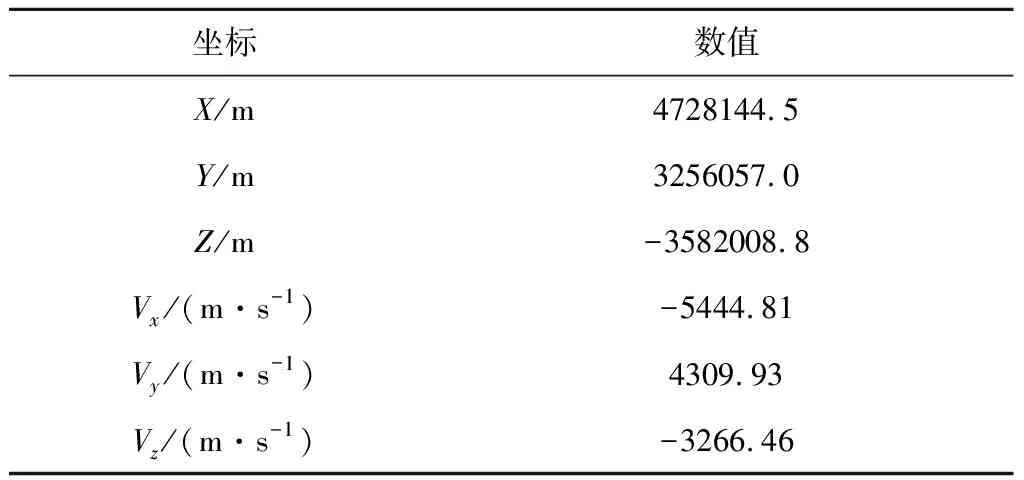
表1 空間實驗室初始位置速度Table 1 Initial state for the space laboratory

2.2 PCE模型階數(shù)

為考察不同階數(shù)PCE模型的精度，首先將樣本點的數(shù)目設(shè)置為10000。各樣本點對應(yīng)的初始軌道根據(jù)其概率分布計算得到。由于僅位置和速度存在誤差，因此PCE模型維數(shù)d=6。采用不同階數(shù)的PCE模型進行預(yù)報，分別預(yù)報1天、7天，并統(tǒng)計均值和標準差。圖1給出了不同階數(shù)PCE模型計算結(jié)果的相對變化值。從圖1可以看出，隨著PCE階數(shù)的增加，均值和標準差的計算結(jié)果相對變化逐漸減小。預(yù)報1天時7階PCE模型相對于6階PCE模型均值相對變化為10-14量級，標準差相對變化為10-11量級；預(yù)報7天時7階PCE模型相對于6階PCE模型均值相對變化為10-8量級，標準差相對變化為10-7量級。

圖2給出了7階PCE模型各項系數(shù)的歸一化值|bi/b0|。若系數(shù)歸一化值不收斂，說明需要更高階的PCE模型才能夠達到較好的近似效果。從圖2可以看出，隨著項數(shù)的增加PCE系數(shù)值逐漸減小，PCE方法趨于收斂。與預(yù)報7天相比，PCE系數(shù)收斂速度在預(yù)報1天時更快。在同樣的精度指標要求下，預(yù)報時間越長，所需PCE模型階數(shù)越高。實際工程應(yīng)用中，越高階的PCE模型項數(shù)越多，計算量越大，因此PCE階數(shù)的選擇需要綜合考慮精度和計算效率的影響。

2.3 樣本點數(shù)目

為考察樣本點數(shù)目對PCE模型的精度影響，本節(jié)的樣本點數(shù)目設(shè)置為可計算得到PCE模型系數(shù)的最少樣本點數(shù)目。參照第2.1節(jié)，d維p階PCE模型所需的最少樣本點數(shù)目為(d+p)!/(d!p!)。與第2.2節(jié)中10000個樣本點的結(jié)果進行比較，結(jié)果如圖3所示。從圖3可以看出，PCE模型階數(shù)越低，采用最小樣本點計算得到的相對誤差越大。預(yù)報1天時4階PCE模型的標準差相對誤差達到10-5量級；預(yù)報7天時5階PCE模型的標準差相對誤差達到10-5量級。綜合考慮精度和計算效率的影響，5階PCE模型效果最佳。

圖1 PCE模型計算結(jié)果相對變化值(基于二體模型)Fig.1 Relative difference in the PCE results (using the two-body model)

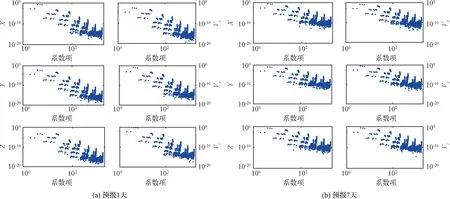
圖2 7階PCE模型各項系數(shù)歸一化值(基于二體模型)Fig.2 Normalized coefficients for the seven order PCE model(using the two-body model)

2.4 與MCS方法的比較

工程應(yīng)用中，MCS方法是軌道預(yù)報誤差分析采用較為廣泛的一種方法，該方法需要較多的樣本點才能滿足一定的精度要求，本節(jié)將最小樣本點的5階PCE方法與MCS方法進行比較，驗證PCE方法的計算效率和精度。

圖4給出了MCS方法計算結(jié)果相對于樣本點數(shù)目的變化值。圖5給出了PCE方法與MCS方法的比較結(jié)果(僅給出了標準差，均值結(jié)果類似)。可以看出，隨著樣本點數(shù)目的增加，MCS方法的計算結(jié)果趨于收斂至PCE方法的計算結(jié)果。MCS方法使用10000個樣本點才能達到10-4量級的收斂精度，其收斂速度較慢。5階PCE方法只需要462個樣本點便可以達到10-5量級的收斂精度，PCE方法收斂所需的樣本點明顯少于MCS方法，PCE方法計算效率更高。

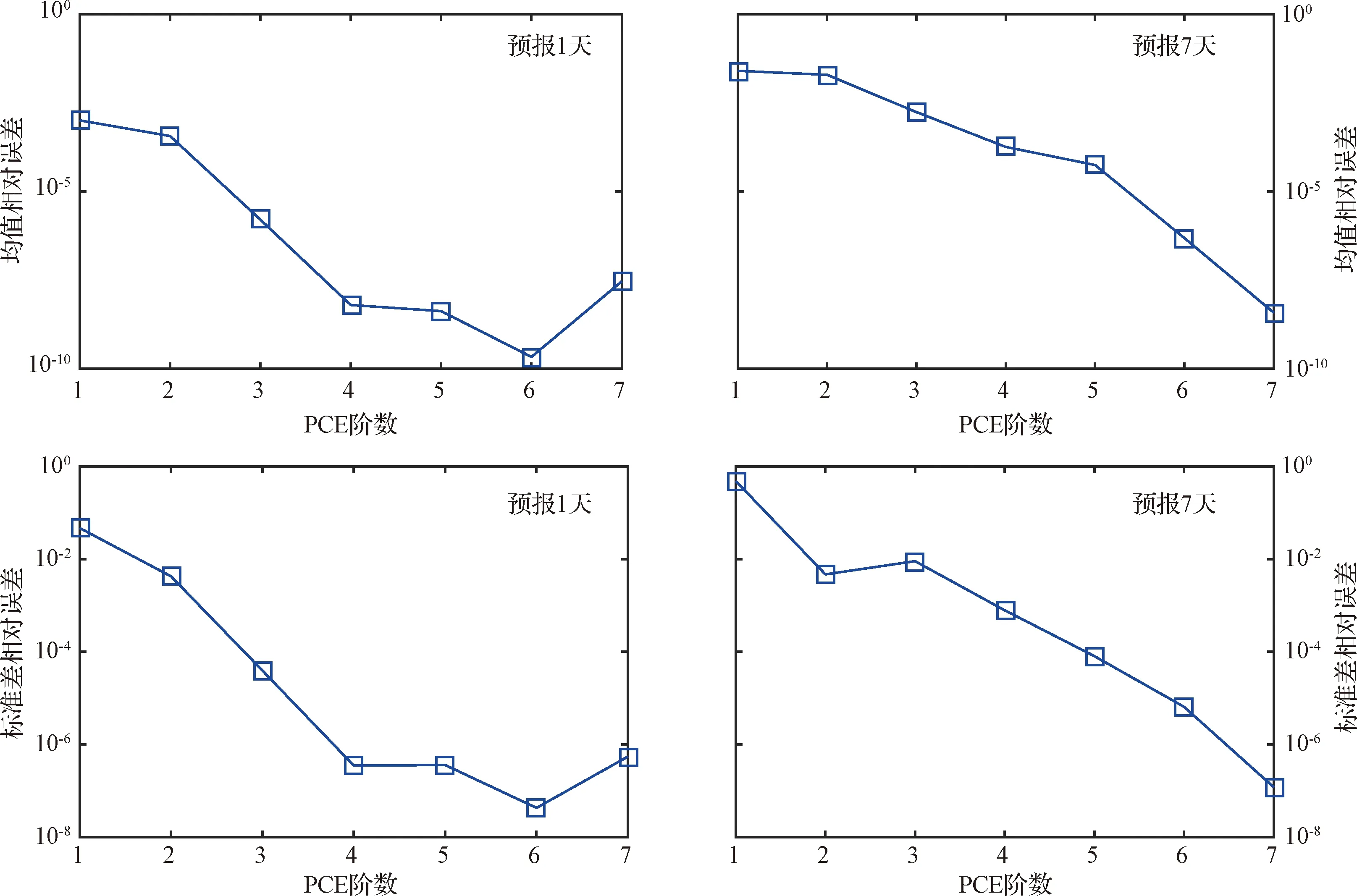
圖3 PCE模型結(jié)果比較(基于二體模型)Fig.3 Comparison of the PCE results (using the two-body model)

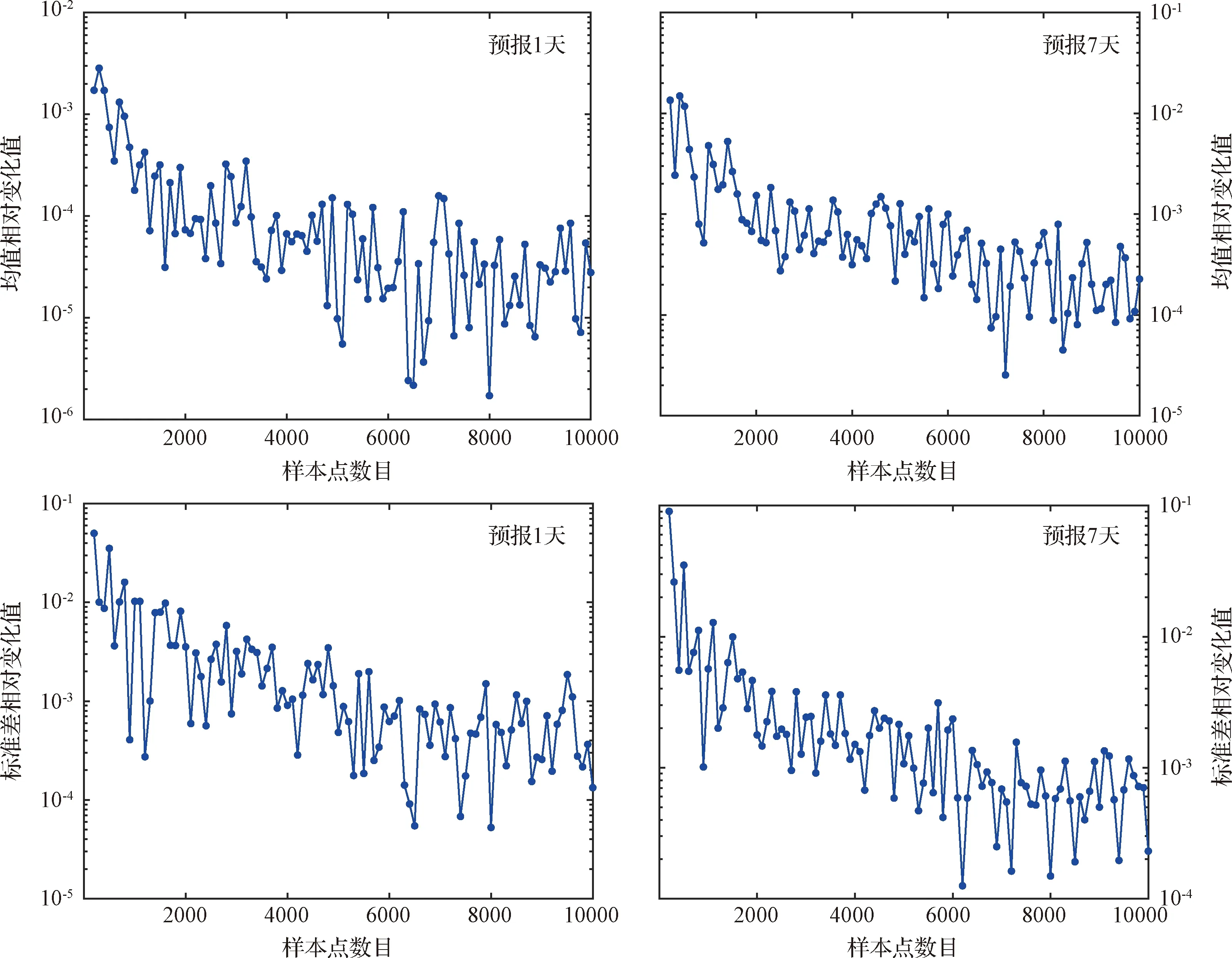
圖4 MCS結(jié)果相對變化值(基于二體模型)Fig.4 Relative difference in the MCS results (using the two-body model)

2.5 與線性傳播方法的比較

線性傳播方法把不確定性傳播模型近似為線性，因此當(dāng)初始位置和速度服從正態(tài)分布時，通過軌道預(yù)報后的位置速度仍然服從正態(tài)分布。表2中比較了最小樣本點的5階PCE方法與線性傳播方法的計算結(jié)果。預(yù)報1天時均值偏差較小，Y，Z和Vx的標準差偏差較大，Z的標準差尤為明顯；預(yù)報7天時均值和標準差的偏差都較大。

第2.4節(jié)中采用MCS方法計算了10000個樣本點預(yù)報1天和預(yù)報7天后的位置速度，其分布如圖6所示。預(yù)報1天和7天后位置速度的分布都有一定程度的傾斜，預(yù)報1天后Z方向位置的分布較為明顯。初始位置和速度誤差在經(jīng)過一段時間的傳播之后，不再服從正態(tài)分布，因此，采用線性傳播方法計算前兩階矩將會帶來較大的誤差。

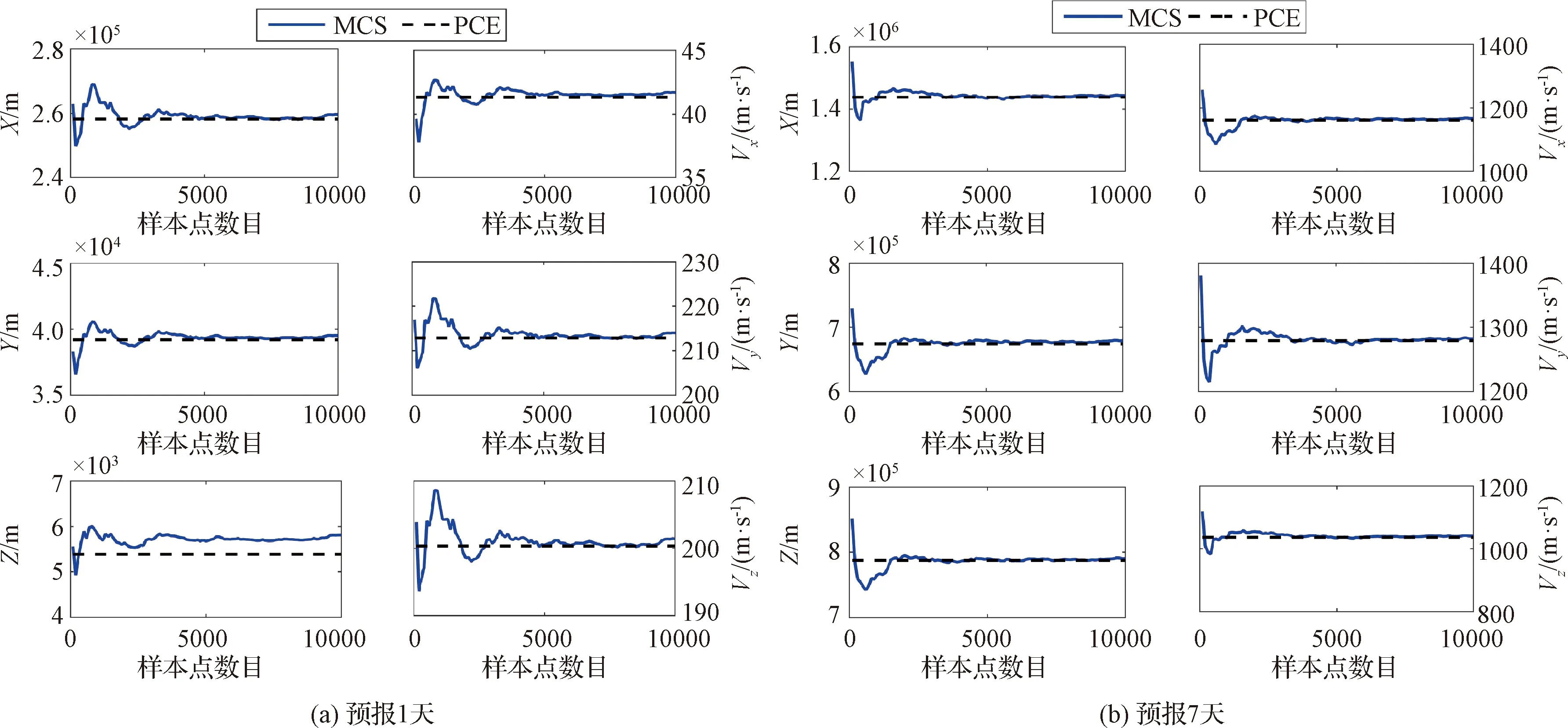
圖5 PCE與MCS的結(jié)果比較(基于二體模型)Fig.5 Comparison of the PCE and MCS results(using the two-body model)

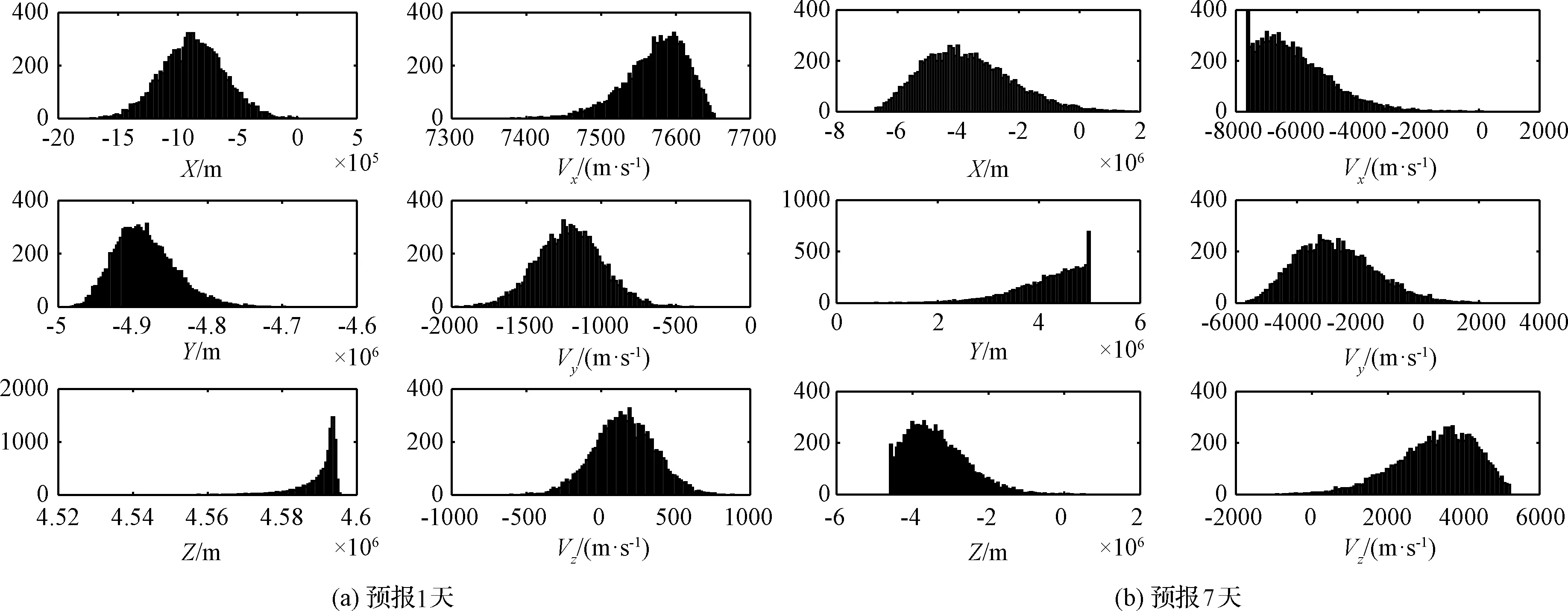
圖6 位置速度分布Fig.6 Distribution of positions and velocities

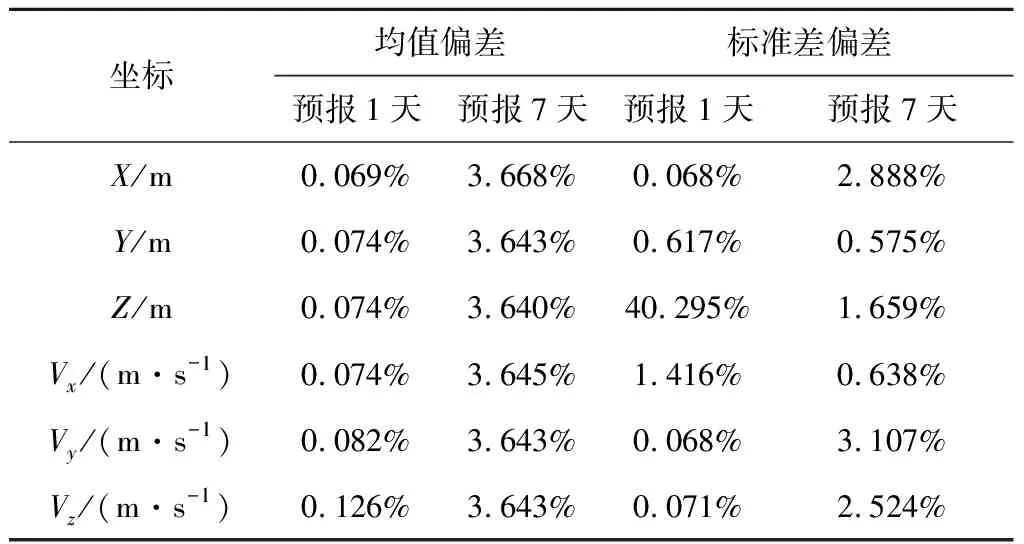
表2 PCE方法與線性傳播方法的比較(基于二體模型)Table 2 Comparison of PCE and linear propagation method(using the two-body model)

通過PCE方法構(gòu)建了軌道預(yù)報不確定性傳播的近似模型。該模型只是簡單的多項式計算，相比于原本的軌道預(yù)報模型計算效率顯著提高。通過構(gòu)建好的PCE模型，不僅能夠計算得到位置速度的前兩階矩，還能夠快速給出位置速度的分布。采用PCE模型計算第2.4節(jié)中10000個樣本點預(yù)報1天和預(yù)報7天后的位置速度，并與MCS的計算結(jié)果進行對比。圖7為軌道坐標系(RTN坐標系)下的散點密度圖。采用PCE模型計算得到的概率分布幾乎和MCS方法得到的概率分布一致，PCE方法構(gòu)建的不確定性傳播模型能夠很好地近似軌道預(yù)報中的不確定性傳播，驗證了PCE方法的有效性。工程中通常用線性傳播方法計算得到的標準差構(gòu)建3σ概率橢圓來描述軌道位置的不確定性[15]，因此圖7也給出了3σ概率橢圓的結(jié)果。從圖7可以看出，采用3σ概率橢圓來描述軌道預(yù)報后的位置分布并不精確，徑向(R方向)誤差相對較大。

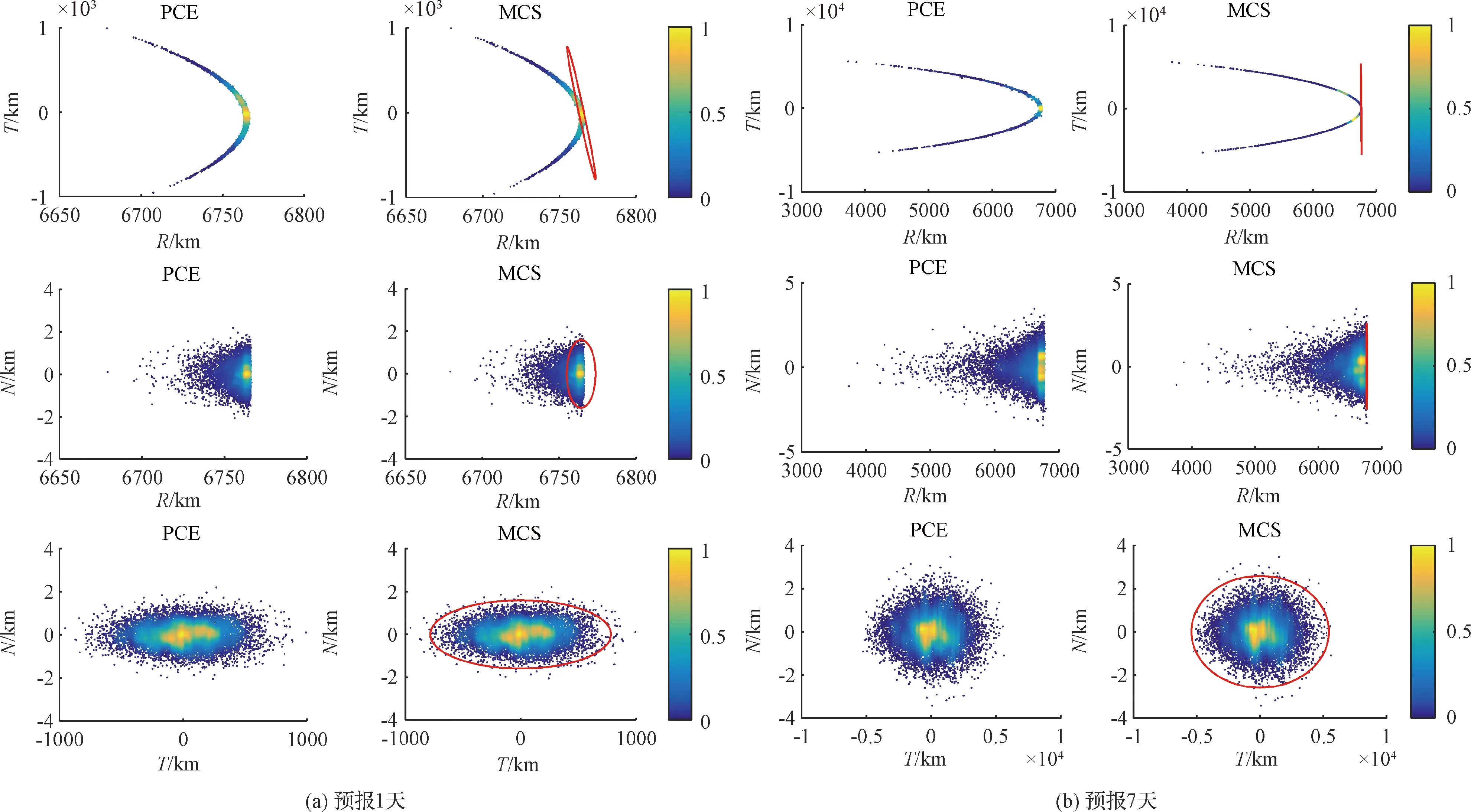
圖7 PCE和MCS結(jié)果分布圖，以及3σ概率橢圓(基于二體模型)Fig.7 Distribution of PCE and MCS solutions, along with 3σ probability ellipsoids (using the two-body model)

3 基于高精度模型的軌道預(yù)報誤差傳播

本節(jié)進一步采用高精度軌道預(yù)報模型對PCE方法的近似效果進行考察。初始位置和速度與第2節(jié)相同，見表1。考慮初始位置、速度以及大氣阻力系數(shù)CD存在誤差，標準差分別為10 m、0.01 m/s和0.1，CD均值設(shè)為2.0。考察預(yù)報1天和7天。PCE模型維數(shù)d=7。

與第2節(jié)類似，本節(jié)使用10000個樣本點和最小樣本點構(gòu)建了不同階數(shù)的PCE模型，并進行了比較。圖8給出了10000個樣本點下5階PCE模型系數(shù)各項系數(shù)歸一化值，可以看出，在100項之后，系數(shù)值的量級都在10-10左右波動，增加PCE模型的階數(shù)并不能顯著提高近似效果。3階PCE模型總項數(shù)為120項，綜合考慮精度和計算效率的影響，選取3階PCE模型。通過對比最小樣本點下不同階數(shù)PCE模型的計算結(jié)果得到，預(yù)報1天時3階PCE模型相對于2階PCE模型均值相對變化為10-11量級，標準差相對變化為10-8量級；預(yù)報7天時3階PCE模型相對于2階PCE模型均值相對變化為10-10量級，標準差相對變化為10-7量級。

圖9給出了PCE方法與MCS方法的比較結(jié)果(僅給出了標準差，均值結(jié)果類似)，隨著樣本點的增加，MCS方法計算結(jié)果逐漸趨于PCE方法的計算結(jié)果，且MCS方法的收斂速度較慢，所需樣本點數(shù)目較多。

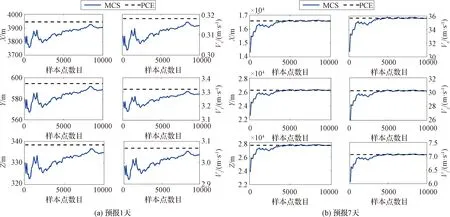
圖9 PCE與MCS的比較(基于高精度模型)Fig.9 Comparison of the PCE and MCS (using the higher fidelity model)

圖10對比了軌道坐標系(RTN坐標系)下PCE、MCS以及線性傳播方法得到的結(jié)果。PCE模型計算得到的概率分布幾乎和MCS方法得到的結(jié)果一致。本節(jié)中初始速度誤差比第二節(jié)中小兩個量級，預(yù)報1天時采用線性傳播方法得到的3σ概率橢圓也能夠較好地描述位置速度的概率分布，但在預(yù)報7天時誤差相對較大。通過與MCS方法及線性傳播方法的對比可知，PCE方法能夠很好地解決基于高精度模型軌道預(yù)報誤差傳播的問題，驗證了PCE方法的有效性。

4 結(jié) 論

本文以空間實驗室為研究背景，將PCE方法應(yīng)用于軌道預(yù)報誤差分析。通過構(gòu)建PCE模型對軌道預(yù)報的不確定性傳播過程進行近似，進而對軌道預(yù)報后航天器位置和速度的誤差進行分析。針對二體模型和高精度模型，分析了不同PCE模型階數(shù)、預(yù)報時長以及樣本點的數(shù)目對構(gòu)建PCE模型的影響。將PCE方法與MCS方法和線性傳播方法進行了對比，結(jié)果表明PCE方法有較好的非線性近似能力，且計算效率要明顯高于MCS方法，驗證了PCE方法應(yīng)用于空間實驗室軌道預(yù)報的有效性。

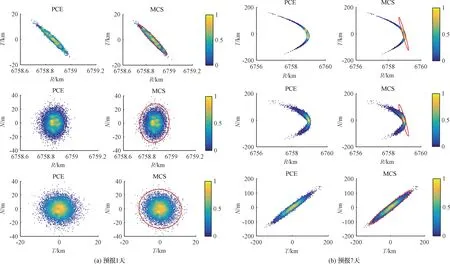
圖10 PCE和MCS結(jié)果分布圖，以及3σ概率橢圓(基于高精度模型)Fig.10 Distribution of PCE and MCS solutions, along with 3σ probability ellipsoids (using the higher fidelity model)

本文的軌道預(yù)報只考慮了初始時刻位置速度、以及大氣阻力系數(shù)的不確定性。在本文的研究基礎(chǔ)上可以進一步細化不確定性模型，考慮例如重力場、光壓、空間環(huán)境等模型參數(shù)存在不確定性時對構(gòu)建PCE模型所帶來的影響。另外，本文在樣本點的選取上使用了最小樣本數(shù)目的方式，還可以進一步研究根據(jù)軌道動力學(xué)中不確定性的傳播規(guī)律序貫添加樣本點以達到更好的近似效果和計算效率。本文的研究工作為這些問題的研究提供了較好的基礎(chǔ)。