機械臂運動學建模及解算方法綜述
冷 舒,吳 克,居鶴華
(1. 南京航空航天大學航天學院,南京 210016;2. 北京空間飛行器總體設計部,北京 100094)
0 引 言
隨著機械臂在工業、航天等多個領域的廣泛應用[1-2](見圖1),提高機械臂運動控制系統的精度引起了相關研究人員的廣泛關注,其中機械臂運動學建模及求解是決定運動精度的重要一環。運動學從功能上可分為正運動學及逆運動學,正運動學通過給定機械臂的關節角度獲取機械臂桿件某一點的位置及姿態。逆運動學通過給定機械臂末端的位置及姿態計算機械臂各關節的運動量,其中逆運動學是運動學建模及求解的難點。機械臂正運動學模型為機械臂遞歸動力學控制的每一步提供了桿件質心位置及關節位置,而機械臂逆運動學與機械臂運動規劃是密不可分的。圖2體現了機械臂運動學在整個機械臂力位控制系統中的作用。
工程中絕大多數機械臂都是串聯結構,故本文主要調研該類型結構的運動學建模方法。求解方法主要分為解析法、數值解法及人工智能法。

圖1 航天機械臂及工業機械臂Fig.1 Manipulators in aerospace and industry
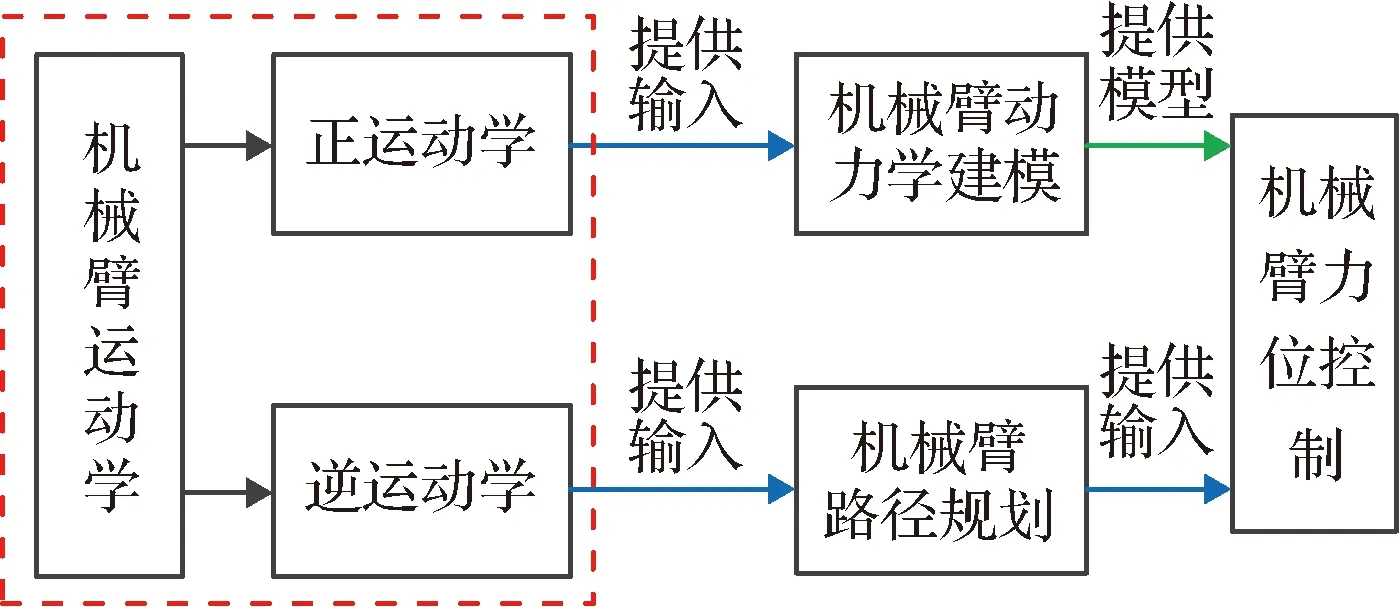
圖2 機械臂運動學在力位控制系統中的作用Fig.2 Manipulator kinematics in the control system
1 機械臂運動學建模的數學基礎
對機械臂運動學建模時通常采用兩種坐標系。其一是1965年Denavit及Hartenberg在文獻[3]中提出的DH系,其二是結合零位參考系的POE模型。
1.1 DH系
DH系及DH參數表示了用關節連接的相鄰兩根桿件間的坐標系及坐標參數。其中ak,ck,αk為結構參數,定義了相鄰兩個關節間的固定值,φk為運動參數,表示關節的運動量。Craig在專著[4]中介紹了建立改進DH系的方法。改進DH系與傳統DH系的不同之處在于,DH參數與桿件之間的對應關系成為主要目標,而DH參數與關節之間的對應關系被視為次要因素。改進DH系在理論推導時物理意義更加明確,方便工程人員應用。后文介紹的各正逆運動學建模及求解方法時,都是以改進DH系為基礎進行推導的。因此本文直接將改進DH系稱為DH系,其定義如圖3所示:
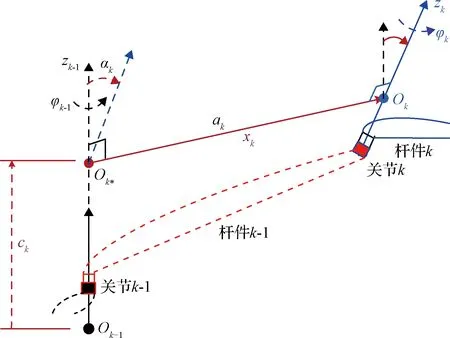
圖3 DH系及DH參數Fig.3 DH frame and DH parameter
給定關節k-1及關節k,改進DH系的建系過程如下:
1)令zk-1及zk分別為關節k-1及關節k的轉動軸。
2)做zk-1及zk的公垂線,定義為xk,其中xk與zk-1交點定義為Ok*,xk與zk交點定義為Ok。
3)點Ok-1與點Ok*的距離記為ck。
4)點Ok*與Ok的距離記為ak。
5)軸zk-1與軸zk間的夾角為αk。
DH系在機械臂運動學建模及求解中起到重要作用,但其存在一個缺點,即建系時相鄰桿件間的DH系旋轉不連續,故在相鄰兩系的z軸平行時,DH系存在奇異性。
1.2 POE模型
文獻[5]中介紹了第二種坐標系,該方法將系統各關節的運動軸矢量統一到同一個笛卡爾坐標系下,該笛卡爾坐標系作為整個系統的參考坐標系,也稱零位參考系。進一步以李群為數學基礎,用指數坐標形式描述剛體的轉動,用旋量描述剛體在三維空間中的六自由度運動。剛體轉動示意圖如圖4所示,其中ω是剛體轉動的轉動軸。該坐標系不存在DH系的缺點,在求解過程中不存在奇異過程。
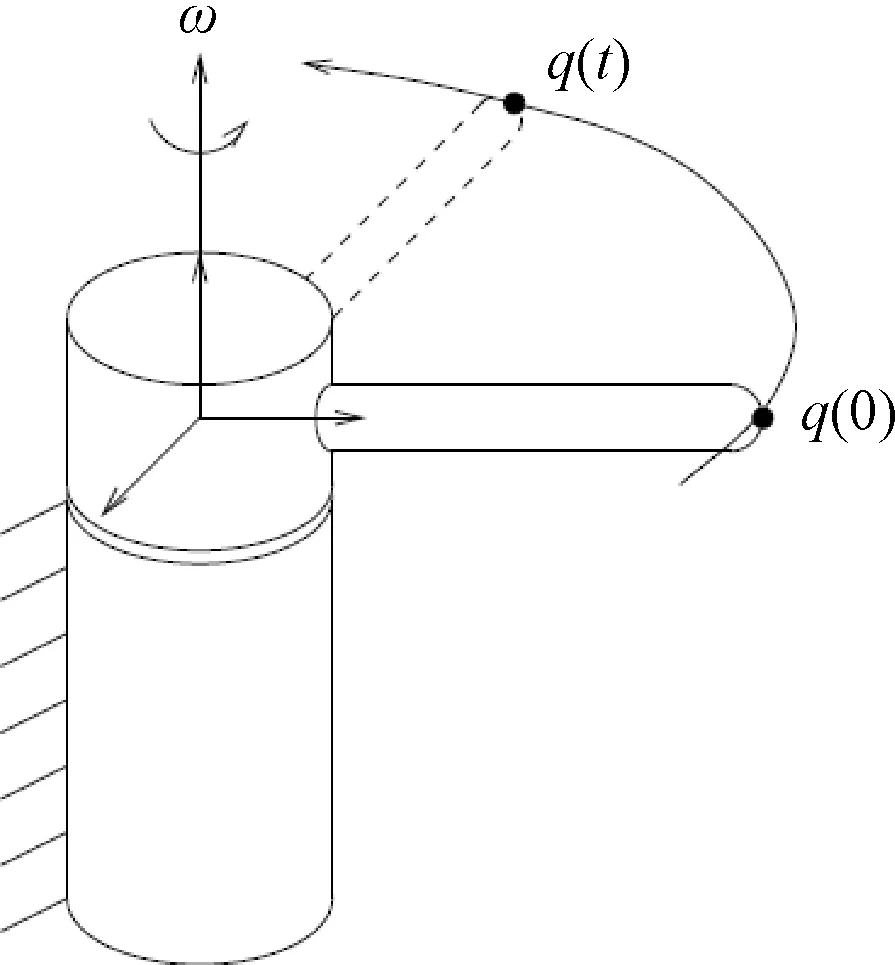
圖4 剛體上一點繞ω軸的轉動[5]Fig.4 A point in the rigid body rotate around axis ω[5]
2 機械臂正運動學
求解n自由度機械臂正運動學時,已知機械臂所有關節角組成的矢量φ,機械臂桿件k末端位姿矢量為sk,s={s1,…,sk}。則系統正運動學模型用公式描述:
s=f(φ)
(1)
因機械臂具有串聯構型,由文獻[4]可知其末端位姿能通過運動學的正向傳播求得,故首先建立相鄰桿件間的關節運動學模型。假設關節k及桿件k對應的DH系為Fk,關節k繞zk轉動φk時,Fk-1轉動至Fk的旋轉變換陣為:
(2)
其中,λk=cos(φk),μk=sin(φk),而Fk系原點Ok的運動值相對于Fk-1的原點Ok-1為:
(3)
用齊次變換陣k-1Tk描述體k運動,記為:
(4)
若使用文獻[5]中介紹的基于POE模型的剛體運動學表示法,則關節k轉動φk時,k-1Qk表示為:
1+sin(φk)ωk+(1-cos(φk))(ωk)2
(5)
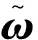
剛體的平移值k-1rk=[xk,yk,zk]是k系原點在k-1系下的坐標,如圖5所示。

圖5 POE模型中的平移Fig.5 Translation in the POE-based model
對于機械臂的任意桿件l,其末端位置sl表示為:
(6)

3 機械臂逆運動學
與式(1)類似,nDOF機械臂逆運動學模型也可用一個通式表示:
φ=f-1(s)
(7)
其中,s={s1,…,sn,q1,…,qn},表示機械臂的末端位置及姿態。
3.1 幾何法
最早出現的求機械臂逆解的方法是幾何法,該方法不建立關節及桿件的DH系及DH參數,而是根據桿件間的平面幾何關系建立機械臂關節角與末端位置的約束方程。文獻[7]中提出了平面二自由度機械臂的逆運動學求解,如圖6所示。其中兩桿件的長度分別為l1,l2,兩個關節角度分別為θ1,θ2,根據系統的幾何關系列寫機械臂的運動學方程,從而得到機械臂末端位置與關節角的關系。在實際應用中,根據已知的機械臂末端平面位置,反解兩個關節的角度分別為:
(8)
(9)
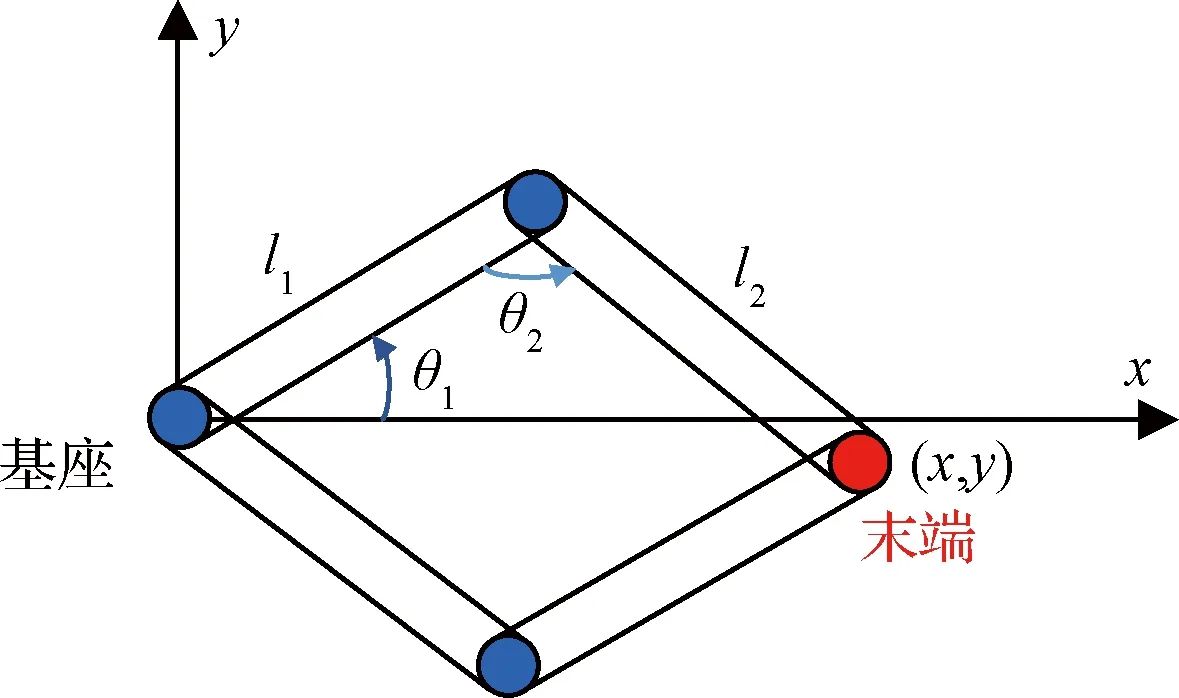
圖6 平面2DOF機械臂的幾何法解示意圖Fig.6 Geometry approach for a planer 2DOF manipulator
文獻[8]針對冗余自由度的平面機械臂提出了利用幾何法求機械臂逆解的方案,其定位方程為:
xtp=l1cos(θ1)+l2cos(θ1+θ2)+…+
lncos(θ1+…+θn)
ytp=l1sin(θ1)+l2sin(θ1+θ2)+…+
lnsin(θ1+…+θn)
(10)
為求解方程,假設θ1=α,θ2=θ3=…=θn=θ,引入兩個參數
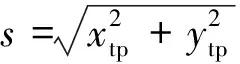
(11)
其中,s只與θ相關,而γ用來求解α。從而得到相應的解。該機械臂構型及求解示意圖如圖7所示。
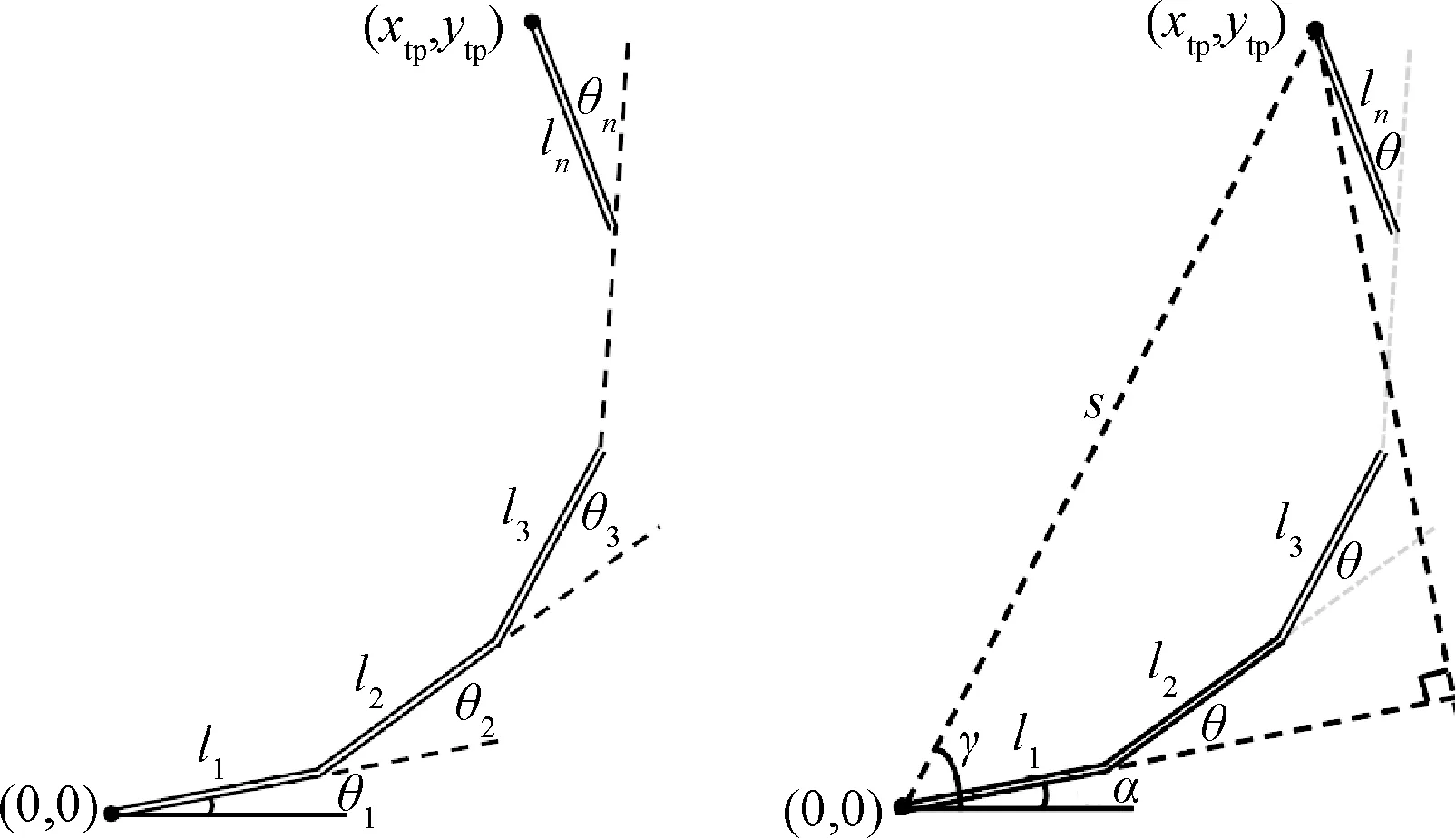
圖7 nDOF平面機械臂及其求解示意[8]Fig.7 Geometry approach for a planer nDOF manipulator[8]
幾何法為解析法在平面上的特例,部分文獻將其歸結至解析法中,也有文獻將其單獨作為一種方法介紹。從上文中的兩個例子可知其實用性較弱,下文將介紹工業及航天領域中最多應用的兩種求機械臂逆運動學解的方法—解析法及數值法。
3.2 解析法
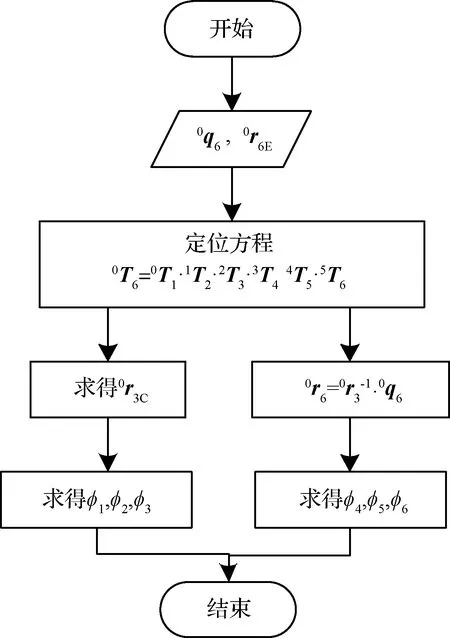
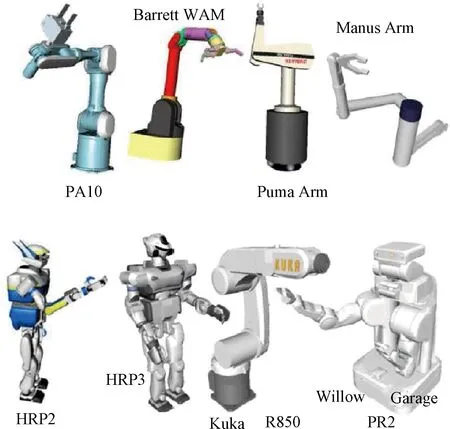
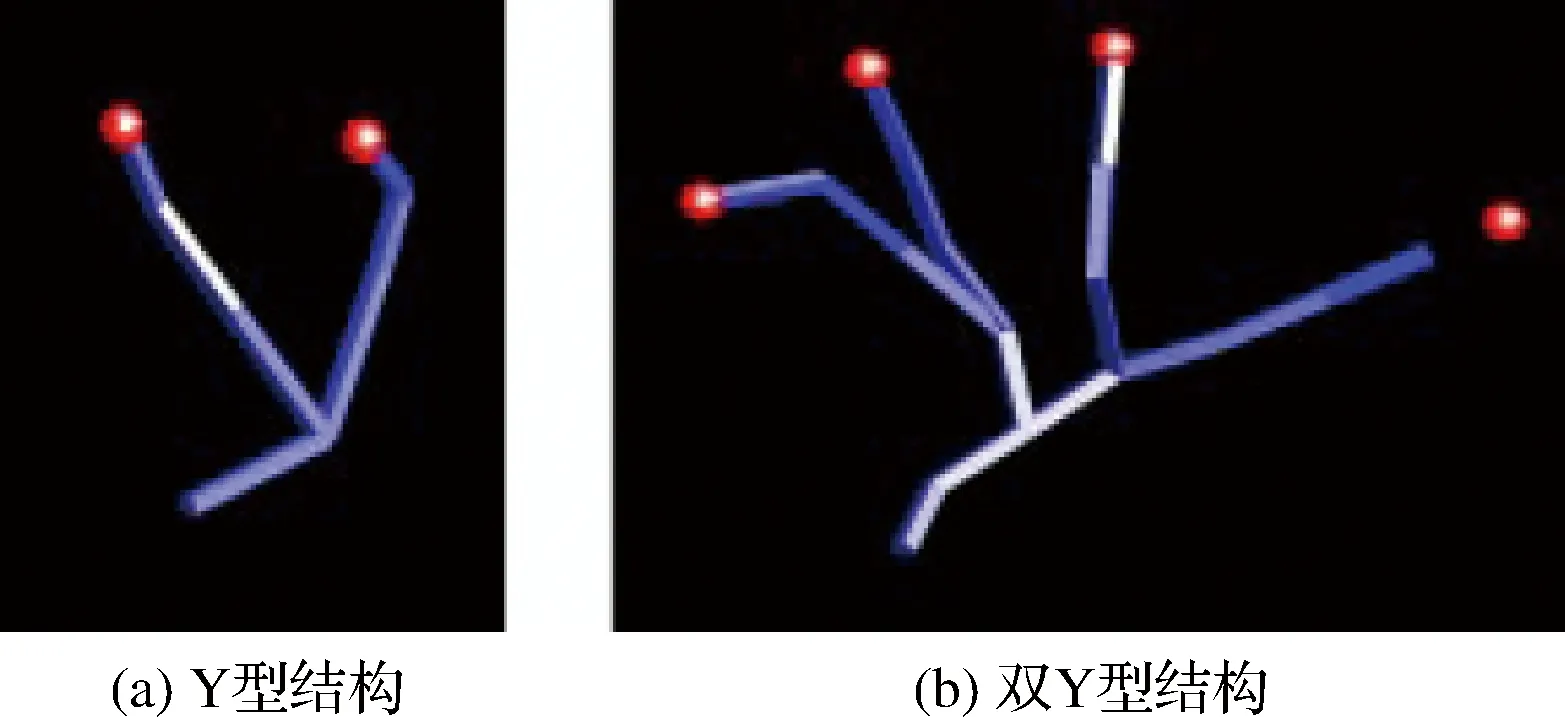
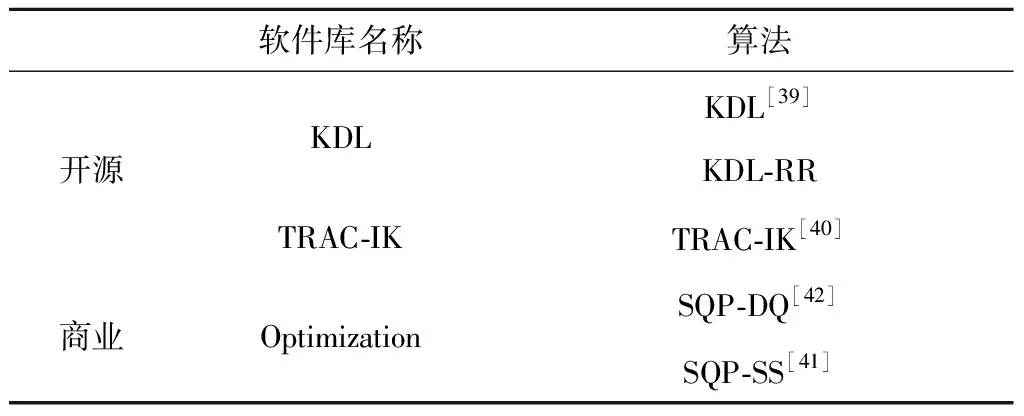
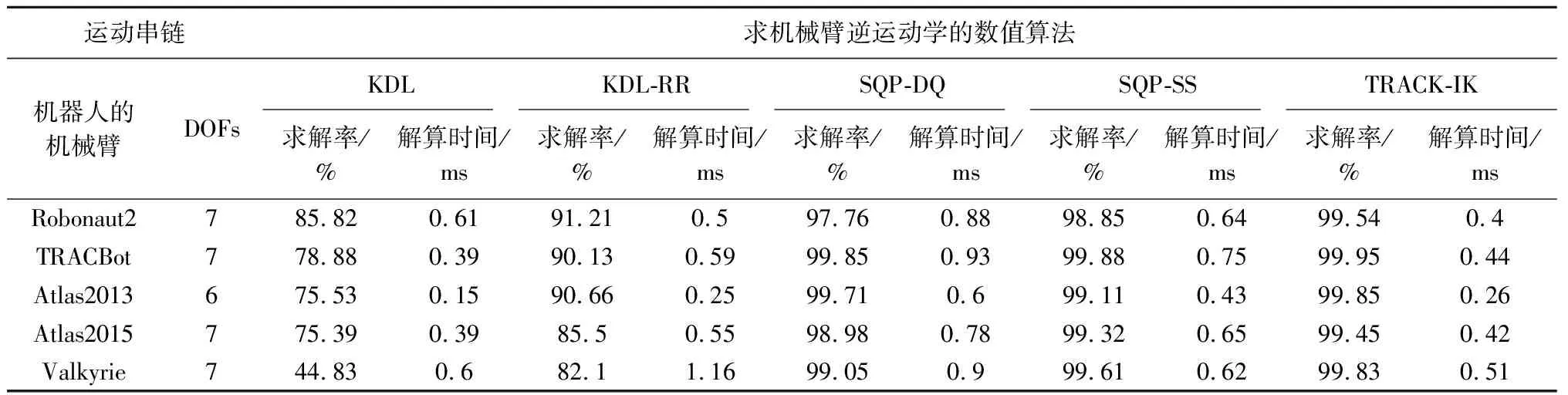
利用解析法求機械臂逆運動學解時,首先需要分析機械臂的關節個數及其結構。在工業及航天領域中,三軸到七軸的機械臂都得到大量應用,其中三軸到五軸機械臂主要用于深空探測任務中[9],如我國嫦娥三號機械臂為三軸機械臂[10],美國的洞察號安裝了四自由度機械臂,勇氣號與機遇號火星巡視器安裝了五軸機械臂[11-12]。工業機械臂與空間站機械臂通常具有六到七個關節。其中六自由度機械臂因具有工作空間大、運動靈活、非冗余等特點成為研究的首要目標。而超過六軸的機械臂為冗余機械臂,常看作6+m構型,七軸機械臂通常用6+1構型研究。因此本文主要介紹六自由度(DOFs)機械臂的逆運動學解法。對于關節個數3 0T6=0T1·1T2·2T3·3T4·4T5·5T6 (12) 接著根據末端位置矢量0r6E及姿態四元數0q6,確定機械臂腕心位置0r3C,再根據腕心位置確定前三軸角度φ1,φ2,φ3,如式(13)所示。得到前三軸的姿態四元數0q3后,先根據0q6確定后三軸的姿態四元數3q6,再根據姿態對齊求得后三軸角度φ4,φ5,φ6。 圖8 機械臂分類Fig.8 Classification of the manipulator (13) (14) 最后將六個關節的所有角度組合在一起,得到16個實數解。具體流程如圖9所示。 圖9 6R機械臂逆運動學求解流程圖Fig.9 The flowchart for solving inverse kinematics of6R manipulators 解耦機械臂是一種理想構型,但因機械加工及機構裝配存在誤差,實際應用中幾乎不存在解耦構型的機械臂。用上述方法求非解耦機械臂的逆解會導致關節角存在計算誤差,從而在實際應用出現定位精度偏低等問題,進而可能出現碰撞等嚴重問題。此時求通用機械臂逆運動學的解析法應運而生。 斯坦福大學的Raghavan及Roth[13]提出了一種通用六軸機械臂的消元法,該方法首先列出如式所示的機械臂定位方程組,其中每個方程是一個六元二次多項式方程。作者先將方程變為: (15) 根據0T6最后兩列與φ6無關的特點可以將φ6消元。此時等式左側只有φ1,φ2等式右側有φ3,φ4,φ5,表達式如式所示:其中s1表示sin(θ1),c1表示cos(θ1)。 (16) 其中,P是14×8階常數矩陣,而B是含φ3的14×9階矩陣。此時φ1,φ2可以用φ3,φ4,φ5進行替換,接著再消元φ4,φ5得到一個只有φ3的16階多項式。求解該多項式得到φ3的所有解,最后將φ3依次代入式中,迭代求得其他各關節的所有解。仿真結果表明該方法對于六軸通用機械臂依然成立。Manocha等[14]在文獻[13]的基礎上優化了求解該方程的方法。將式消元φ1,φ2后得到。 (17) 其中,Axy為3×3的矩陣,b為12×1的矢量,0為3×3的零矩陣。A中的每一個元素都只含有φ3,φ3為A的特征根。式成立的條件為det(A)=0,其中det(A)表示矩陣A的行列式。det(A)=0也可得到一個只有φ3的16階多項式,求解得到φ3的所有值。利用該方法求解速度可提升至11ms。上述兩種方法都以DH系為數學基礎建立了逆運動學模型,但由DH系的缺陷可知,它們在求解過程中存在奇異性。 隨著雙四元數概念[15]的提出,Husty等[16]利用雙四元數結合Segre流型求通用6R機械臂的逆解。他們將一個6R串聯機械臂從中間分開變為二個開環的3R串鏈,斷點左右的兩個坐標系ΣL=ΣR。上述3R串鏈都是只用一個參數表示的Segre流型,每個流型由四個超平面組成。兩個Segre流型的16個交點表示機械臂逆運動學的16個逆解,超平面方程由四個參數化表示的矢量的行列式等于零得到。數值仿真結果表明,16個逆解中有二個為實數解而其他14個為虛數解。北京郵電大學的Qiao等[17]利用雙四元數表示機械臂的定位方程,使得該方程變為關節角組合的多重線性型,并通過Dixon結式求解該定位方程。其數值仿真結果表明,16個解中有四個解是實數解有12個解為虛數解。上述方法求解速度較快,但表達式比較復雜,在實踐中需要工程人員有很強的數學基礎才能順利求解。 對于上文提到的解析法,在實際應用中有比較成熟的開源庫解決上述問題。如文獻[20]中提到用Matlab的Robotics Toolbox庫求解6R機械臂的逆運動學解,其平均計算時間為0.27 ms。文獻[21]中用ikfast軟件庫計算機器人逆運動學。圖10展示了可用ikfast計算逆運動學的機器人種類,表1介紹了每種機器人計算逆解的時間及經過10000次隨機試驗得到的計算成功率。由表1可知,ikfast可以成功求得任意六軸機械臂的逆解,精度達10-7m。在求解七軸機械臂時精度仍能保持在10-7m,但無法保證成功率達到100%。 雖然用解析法求機械臂逆運動學解能高效地得到機械臂在期望位姿的全部逆解,但現有的方法都存在兩個缺陷。(1)在求解過程中無法滿足避障約束,需要在求得所有解后對其進行后處理,篩選出可行解。(2)該方法很難處理在動態環境下的機械臂逆運動學求解。在深空探測任務中,行星車不斷接近探測目標時,二者之間的相對位姿是時刻變化的,在不同時間點求得機械臂的期望位姿是不同的。因此應用該方法執行任務時,必須等到行星車與探測目標相對靜止后,再用解析法求機械臂逆運動學解,最后實現機械臂運動路徑規劃。 圖10 文獻[21]中用ikfast計算逆運動學的機械臂Fig.10 The manipulator inverse kinematic calculatedby ikfast[21] 機械臂類型DOFs求解時間/(μs)成功率PA1067100%Barrett WAM66100%Puma Arm66100%Manus Arm66100%HRP27699.5%HRP37699.5%Kuka R85065100%Willow Garage PR27698.2% 多剛體逆運動學有多種數值解法,如雅可比迭代法、牛頓法及混合逆運動學法等,但在機械臂求逆解時幾乎都采用雅可比迭代法。因此本文提到的數值解法專指雅可比迭代法的研究現狀。雅可比迭代法[22]對于機械臂的關節數及結構沒有特別要求,且適用于機械臂基座與目標間存在相對運動的系統的逆運動學求解,因此在六軸空間機械臂[23]、n軸空間機械臂[24]及深空探測[25]等領域的理論及工程實踐中有不少應用。用數值法可以得到機械臂從起始位姿到目標位姿的一個包含運動路徑的逆解,因此一般直接用數值法進行運動規劃。在數學上無法證明該逆解是最優解,推測求得的解是次優解或最優解的逼近。 雅可比迭代法的基本公式仍為式,主要原理為通過雅可比矩陣J線性逼近一個可行解, (18) (19) 進一步可以得到關節角度微小變化Δφ對機械臂末端位置變化Δs的影響。 Δs≈J(φ)Δφ (20) 因在機械臂規劃過程中,機械臂末端位置與期望位置之間存在誤差e,通過對微小角度的變化進行迭代求解,可以逐步縮小誤差逼近期望位置。 e=J(φ)Δφ (21) 由于機械臂末端位置是一個三維矢量,而機械臂關節數量不定,故雅可比矩陣J不一定是方陣。而迭代求解關節位置時需要求J-1,非方陣的J無法求逆。針對該問題,研究人員們想出多種解決方案。Unzueta等[26]提出雅可比轉置法,通過引入一個與雅可比矩陣相關的常數α與雅可比矩陣的轉置JT相乘的結果近似J-1,保證關節變量與末端位置之間的關系如式所示。式中〈x,y〉表示矢量x,y的內積。 (22) 數值仿真結果表明α應取較小值,否則系統末端將存在震蕩或不連續性。Buss[27]提出利用雅可比矩陣的偽逆近似雅可比矩陣的求逆。 Δφ=J?e (23) 其中,J?表示為J的偽逆矩陣。偽逆方法雖然解決了非方陣的雅可比矩陣的求逆問題,但在奇異點附近存在不穩定性。因此當目標位置在奇異點附近時,利用上述方法會導致求解結果無法收斂。Liegeois[28]及Maciejewski等[29]采用零空間法改進前文提到的偽逆法,他們將矩陣(I-J?J)投影至J的零空間上,I為單位陣。即對任意矢量v,J(I-J?J)v=0n,則方程改寫為 Δφ=J?e+(I-J?J)v (24) 該方法通過選擇不同的v有一定幾率求出另一個解。雖然它提高了偽逆算法的實用性,但其在奇異點附近穩定性依然很差。 為了改善偽逆算法在奇異點處穩定性差的缺陷,Wampler[30]提出了Levenberg-Marquardt(LM)算法,Nakamura等[31]采用阻尼最小二乘法(DLS)。 Δφ=JT(JJT+λ2I)-1e (25) 上述方法不但可以減輕機械臂運動中的抖動,還可以改善偽逆算法在奇異點附近的表現。文獻[32]用試驗表明LM算法優于雅可比轉置法及偽逆求解法,但其存在收斂速度慢且對于目標的跟蹤精度較差的缺點。 也有不少學者針對雅可比矩陣采用了奇異值分解法(SVD),文獻[33]通過SVD法對偽逆矩陣進行分解 其中,σi=0是奇異條件。Maciejewski[34]結合SVD法改進了DLS法,他利用SVD方法分解阻尼最小二乘矩陣: JT(JJT+λ2I)-1=VEUT= (26) 結果表明,在奇異點附近利用SVD方法計算機械臂的運動路徑比利用偽逆法得到的結果平滑許多,彌補了偽逆求解法的不足。 此外在實際工程中,機械臂的關節存在角度約束,運動空間內存在碰撞約束等。Welman等[35]提出了解決關節角度約束的方法。文獻[36]及[37]分別提出了零空間飽和法,該方法有效的解決了關節角度約束及運動空間內碰撞的問題,上述方法是結合了優化方法的雅可比迭代法。 文獻[38]中通過一個仿真試驗對比了雅可比矩陣轉置法與阻尼最小二乘法之間的區別,雖然選擇的研究對象不是串聯機械臂而是更為復雜的并聯結構。但該示例仍可說明數值解法的特點。圖11展示了Y型及雙Y型結構的示意圖,計算時間如表2所示。從結果可知雅可比轉置法比阻尼最小二乘法計算時間更短。 圖11 研究對象[32]Fig.11 The Y type and double-Y type structures[32] 到目前為止,結合優化算法的雅克比迭代法已逐漸成為研究熱點。在實際應用中存在成熟的開源軟件庫及商業軟件庫用數值法結合優化算法求解機械臂逆運動學,幾種常見的軟件庫及其所用的算法如表3所示。其中KDL(Kinematics and dynamics library)中主要用KDL算法[39]及其改進算法KDL-RR(KDL-Random Restarts),TRAC-IK庫[40]中應用的TRAC-IK算法。商業軟件Optimization庫中用SQP(Sequential quadratic programming)算法[41]的改進算法SQP-DQ[42](SQP-double quadratic)及SQP-SS[41](SQP-sum of squares)等。 文獻[40]中比較了幾種軟件庫中不同算法對于機器人逆運動學的求解成功率及平均解算時間。 分別選取五種人形機器人(如圖12所示)的串聯機械臂作為求逆運動學解的對象,用不同算法求逆解的結果如表4所示。其中TRAC-IK庫具有最高的求解成功率及最快的平均解算時間,KDL庫中KDL算法的求解成功率最低。SQP-DQ算法的平均解算時間最長。 表2 兩種方法的計算時間對比[32]Table 2 The runtime of the two approaches[32] 表3 數值法求機械臂逆解所用的軟件庫及其算法Table 3 Illustration of source libraries and their algorithms innumerical method 圖12 測試用的五種機器人[40]Fig.12 The five robot models used for testing[40] 運動串鏈求機械臂逆運動學的數值算法機器人的機械臂DOFsKDLKDL-RRSQP-DQSQP-SSTRACK-IK求解率/%解算時間/ms求解率/%解算時間/ms求解率/%解算時間/ms求解率/%解算時間/ms求解率/%解算時間/msRobonaut2785.820.6191.210.597.760.8898.850.6499.540.4TRACBot778.880.3990.130.5999.850.9399.880.7599.950.44Atlas2013675.530.1590.660.2599.710.699.110.4399.850.26Atlas2015775.390.3985.50.5598.980.7899.320.6599.450.42Valkyrie744.830.682.11.1699.050.999.610.6299.830.51 從結果來看,雖然運用各種數值算法求逆解的位置誤差與姿態誤差都可達到1e-6(m)及1e-6(deg),但其平均計算誤差是解析法計算結果的10倍,且該方法也存在著一個不可避免的缺陷:沒有一種算法的求解率可以達到100%。即使是六軸機械臂,其求解率無法像解析法那樣每次都能找到逆解。造成該問題的原因在于數值法的非線性優化過程過于依賴人為設置或隨機猜想的初始種子。數值法的核心是梯度下降,而種子決定著梯度下降的方向,若種子設置合理,則可以高效地求得理想的結果,若種子設置不合理,甚至會出現無解的情況。 近幾年,隨著人工智能熱潮的掀起,一些學者嘗試采用人工智能的方法求解機械臂逆運動學,期望能用該方法求解特殊結構的機械臂逆運動學。具有特殊結構的機械臂大多用來處理某類特定問題,且該問題無法用常見的機械臂解決,因此無論是航天領域還是工業領域,都有一定的應用價值。 文獻[44]采用傳統遺傳算法及連續遺傳算法求機械臂逆解,遺傳算法的迭代過程中可以得到機械臂的運動路徑。實驗結果表明連續遺傳算法及傳統遺傳算法都可以得到機械臂的逆解,但用第一種方法得到的運動路徑比第二種方法更加平穩。文獻[45]提出了利用人工神經網絡求機械臂逆運動學解的方法。其輸入為機械臂的末端位姿T,輸出為機械臂的關節角度φ。 (27) 結果表明,經過大量訓練后,訓練集Strain的理論正逆互驗精度可以達到10-7m。利用測試集Stest進行測試的結果表明該方法的泛化能力在理論上可以接受,但無法用于工程中。文獻[46]結合了遺傳算法與神經網絡求機械臂逆運動學解。神經網絡的輸入及輸出與文獻[45]一致,但神經網絡的權重值由遺傳算法進行優化。這項改進提高了神經網絡的訓練速度,保證末端位姿誤差能以更快的時間降到目標誤差以下。 文獻[47]介紹了基于Sarsa(λ)強化學習的空間機械臂求逆解及路徑規劃的研究,機械臂的每根桿件都被視作一個可決策的智能體,通過感知機械臂末端與目標的偏差及各桿件和障礙物的距離程度,人工設計獎勵函數,并對各桿件轉動動作進行強化訓練。形成了各智能體的狀態-動作函數表,作為指導機械臂在線運動規劃的依據。結果表明該方法可以指導機械臂在求逆解中滿足避障約束及位置約束。但其無法保證機械臂滿足姿態約束,需要對運動空間進行更細的劃分及設計更完善的獎勵函數才能實現。 到目前為止,人工智能求解機械臂逆運動學的方法還很不成熟。所有人工智能方法都是離線算法,無法實現在線求機械臂逆運動學解及運動規劃。對于神經網絡方法,仿真結果表明訓練后的模型對于訓練集Strain中的數據求逆解的效率及精度都能達到實際應用的標準,但訓練集中并未給出工作空間內的所有點,由于泛化能力較弱,對于不在訓練集內的點的計算效果不佳。此外即使是同一類型的兩臺機械臂A,B,也會有稍許不同,通過訓練機械臂A得到的機械臂逆運動學模型A,很難泛化到機械臂B中。若在實際應用中,將模型A求的逆解作為機械臂B的輸入控制其運動,可能會帶來無法挽回的后果。對于強化學習方法主要存在兩個問題,(1)該方法是基于對環境采樣的算法,機器人所處的環境復雜,采樣效率較低。(2)強化學習的采樣中伴隨著探索,在不確定性很強的環境空間中進行探索,容易損壞機器人。特別是在航天領域,機器人成本很高,因此損壞機器人是無法接受的。所以對于人工智能方法,還需要后續科研工作者繼續努力研究。 目前機械臂正運動學建模及解算方法在理論方面非常成熟。在工程中對機械臂進行正運動學建模時,若輸入的機械臂結構參數與工程模型的實際結構參數之間的誤差小于系統要求的最大精度,則對于機械臂末端位姿的理論計算結果與工程測量結果間的誤差也可以滿足系統的精度。因此,提高機械臂正運動學計算精度的核心是尋找提高機械臂結構參數的精密測量方法。 目前許多科研人員仍對機械臂逆運動學建模與解算進行研究,他們在不同程度上都取得了一定的成果,為機械臂在航天及工業領域的應用奠定了理論及實踐基礎。但求機械臂逆運動學解的工程意義在于為機械臂運動規劃提供輸入。因此尚有以下幾個方面的問題值得關注。 4.2.1解析法的理論研究 建立一套新的滿足機械臂碰撞約束及角度范圍約束的運動學模型。用解析法求機械臂逆運動學解時只需要滿足位置及姿態約束,這兩個約束都是等式約束,因此解一個非線性方程組的根即可得到全部解。但機械臂的工作空間會給予它碰撞約束或角度范圍約束,這些約束是關于桿件位姿的不等式約束。因此在求逆解的過程中,解析法并未考慮與環境的碰撞約束或機械臂的關節角度約束。用該方法求得的逆運動學解中有一個或多個位姿可能與環境發生碰撞。對于該問題,一般是在計算方程組的根后通過解不等式篩除不滿足約束的解,得到滿足各項約束的解,增加了求逆運動學解的計算時間。建立有關機械臂碰撞約束或角度約束的逆運動學模型,將上述模型添加至原來的數學模型中,得到滿足姿態約束的新模型。 4.2.2數值法的工程實踐研究 考慮復雜環境約束下的快速在線求逆解。在航天領域對機械臂的應用中,主要需要考慮在復雜環境的約束中求機械臂的逆運動學解。該約束主要考慮機械臂底座與目標之間存在相對運動的情況,如空間站攜帶的機械臂抓捕與空間站存在相對運動的物體或行星車在星表對感興趣的地貌進行在線探測。此時不但需要考慮機械臂的位置及姿態約束,避障約束,還需要考慮機械臂底座與探測目標之間的速度約束或加速度約束[48]。因此任務空間約束常包括以下幾種,如路徑奇異點規避的約束,在未知環境中運動時,機械臂運動路徑中避障的約束,以及時間、能量等性能最優的約束。對于上述約束,將每一個約束都可表示為一個等式或不等式,對于非凸的約束方程,將其用連續多個凸函數進行分段逼近[49-50]。如運動約束方程中,平動是凸函數,旋轉變換陣為非凸函數,將旋轉變換陣用凸函數逼近,得到一系列凸的約束方程組。利用凸優化[51]的方法求解該運動方程組,得到滿足約束的最優路徑。 4.2.3機械臂逆運動學求解率的理論研究 任務空間[52]約束下的全局逆運動學求解率研究。任務空間約束是對機械臂末端位姿的約束,主要做用于機械臂抓取任務以及抓取后的行為。在任務空間約束下,機械臂求逆解失敗可能有兩種原因。其一是環境約束或運動學約束。如機械臂在抓取目標時無法避免與目標之外的環境碰撞,或在數值法求解的所有運動路徑中,被機械臂抓取物體都無法保證固定姿態,從而導致任務失敗,這種情況也稱為全局求解失敗。其二是初始種子設置不合理導致的求逆解失敗,也稱作局部求解失敗。確定機械臂求解失敗的種類具有十分重要的理論意義,許多科研人員都在研究能識別全局求解失敗的方法。雖然有人提出當求解失敗時,通過多試幾個不同的初始種子再觀測是否存在成功求解,但并無法證明測試的不同種子的數量與求解失敗種類之間存在必然的聯系。該問題的核心在于猜測非線性非凸系統優化的初始鄰域方向。將非凸約束放寬至用凸函數逼近,并將非線性旋轉變換陣Q∈SO(3)的乘法運算通過POE模型轉化為指數系統exp(·)∈SO(3)的線性相加,系統轉化為李代數中的線性系統。上述兩方面是求解該問題的重點。 近年來,隨著凸優化算法成功應用于機械臂逆運動學求解及運動路徑規劃。針對不同約束構造不同的凸函數,解決相應的問題已成為研究熱點。本文提到的解析法及數值法都可與凸優化算法結合。對于解析法,先求解機械臂的逆運動學,再將可行解作為凸優化的終止條件對機械臂進行路徑規劃,最后可得滿足約束條件的最優路徑。對于數值解法,在4.2.2節與4.2.3節中已經介紹了其與凸優化結合可解決的各種問題。利用上述思路,預期可以獲得更多科研成果。 機械臂運動學建模及求解在航天及工業領域都有廣泛的應用。因解析法具有魯棒性更強的特點,廣泛的應用于機械臂基座不運動的工業任務或機械臂基座與目標相對靜止的航天任務中。而對于機械臂基座與目標有相對運動的空間站任務及深空探測任務,因數值解法物易于實現,且對于動基座問題具有更好的適應性,受到研究人員的青睞。人工智能的方法也逐漸應用于該領域,但在理論中還存在諸多問題,并不足以在實際工程中應用,需要科研人員們對該問題進一步研究。本文在總結當前國內外機械臂運動學建模與求解的基礎上,還指明了該領域還需要解決的科學問題,為后續科研工作者提供了研究思路。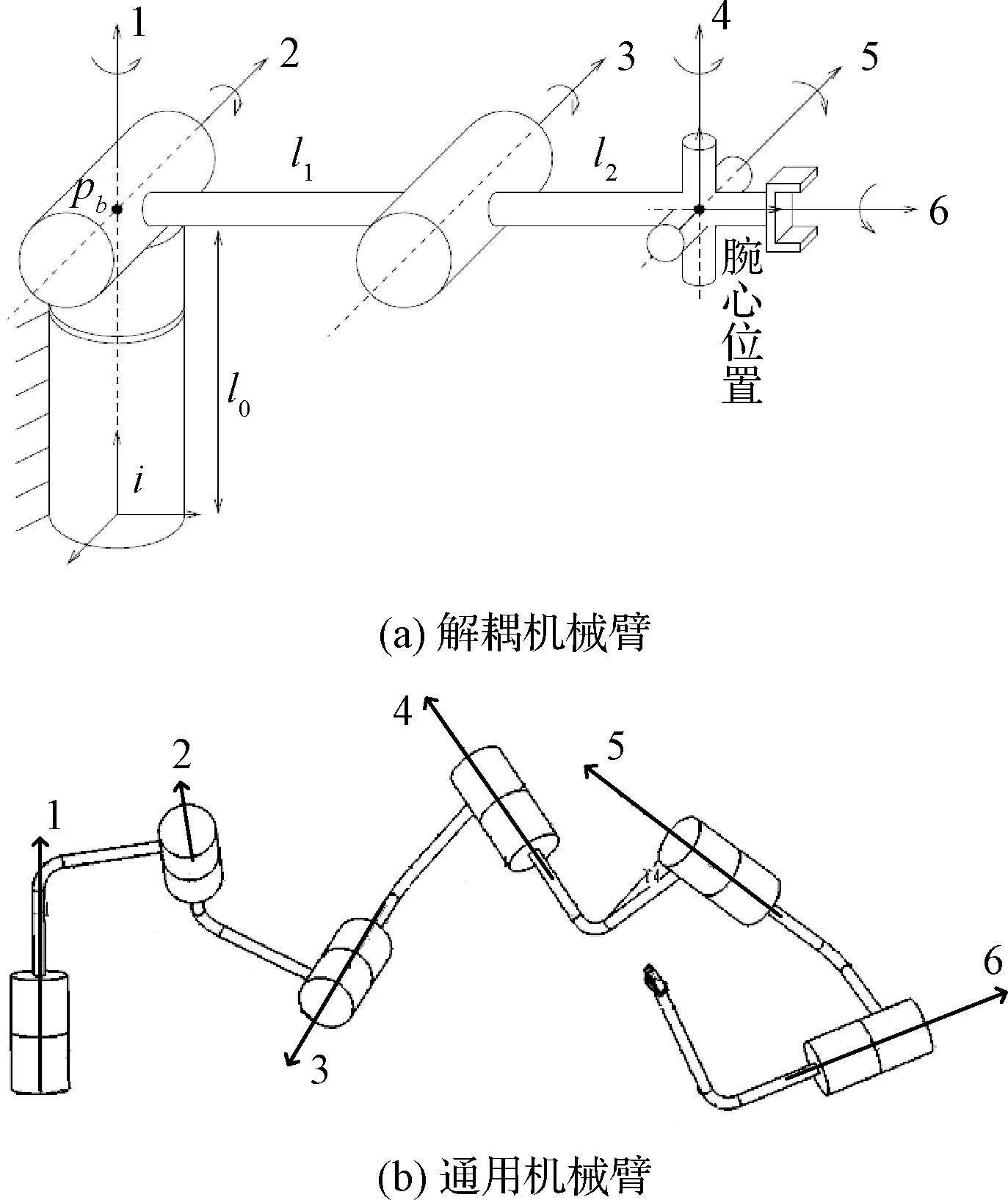

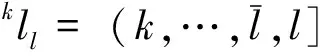

3.3 數值法

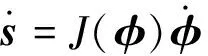



3.4 人工智能方法
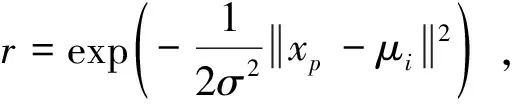
4 機械臂運動學中需解決的關鍵科學問題
4.1 正運動學
4.2 逆運動學
5 結 論

