某型噴管真空羽流流場數值仿真計算研究

趙芃沛，朱 鐳

(陜西空天動力研究院有限公司，西安 710103)

火箭發動機噴管羽流特征對于發動機推力大小、紅外輻射特性[1-3]以及噪聲特性都有直接影響[4-6]。地面條件下羽流流動可以用連續介質模型來描述，用速度、密度、壓力、溫度以及位置和時間等宏觀量建立流場信息的聯系。真空羽流場與地面羽流場差別較大。燃氣從噴管噴出后，在近似真空的環境中無干擾地迅速膨脹，呈球狀擴散，擴散區域大大增加，密度急劇下降，流動狀態也經歷了從連續流區至過渡流區，最終到達自由分子流區的過程。此過程將經歷連續流、過渡流、稀薄流等流動狀態，并伴隨非平衡化學反應和多種激波產生等，使羽流流動狀態的描述以及相關問題的研究變得極為復雜[7-9]。

目前關于真空條件下噴管羽流主要采用DSMC[7]方法和DSMC/CFD混合方法，但目前并沒有成熟的商業軟件采用這兩種方法來計算羽流，考慮到本文最終關注的是羽流外邊界輻射特性對部件的影響，考慮時間和經費成本投入，論文采用了CFD方法來進行計算，可以快速得到初步特性來進行定性分析，在一定范圍內可作為設計的初步參考。

1 計算模型與方法

1.1 計算方法和校驗

本文采用的控制方程為雷諾平均N-S方程(RANS)，該方程的矢量形式為：

流體粘性系數由Sutherland公式確定：

式中:μ0=1.716×10-5NS/m2，T0=121.56 K,μt為湍流粘性系數，由湍流計算模型給出。

湍流模型采用Menter的SSTk-ω模型，其流動方程如下：

式中：Gk表示湍流的動能，Gω為ω方程，Γk和Γω分別代表k與ω的有效擴散項,Yk和Yω分別代表k與ω的發散項。Dω代表正交發散項。Sk和Sω用戶自定義。

采用標準壁面函數法，標準壁面函數法假定：壁面附近粘性底層以外的地區，量綱速度服從對數率分布。

流場求解利用有限體積法離散，定常雷諾平均N-S方程，各方程聯立耦合隱式求解，對流項為二階迎風格式，粘性項采用二階中心差分格式，其他為一階迎風格式。計算結束條件為所有殘差下降3個數量級且不再變化、關鍵截面流量不再變化表示計算結果收斂。

采用以上模型針對文獻[10]中數據進行了校驗計算。該文獻采用DSMC方法對真空羽流進行了數值模擬。將該方法給出的數據與本文采用CFD方法的結果進行了對比，如圖1。

可以看出，在噴管內DSMC方法與CFD方法吻合度較好，因為這一區域滿足連續性假設；而在距離噴管出口較遠的位置，即過渡流區以外以及倒流區的區域有一定的差別。

1.2 幾何模型和計算區域

計算區域和噴管幾何構型如圖2所示。左下角為噴管所在位置。在近似真空的環境條件下，壁面附近的氣流將繞過唇口向管壁上游流動，產生倒流現象，因此將計算域水平方向和豎直方向均設定為2 000 mm。對壁面進行加密，并且對噴管出口處對流向方向進行適當加密。由于結構網格局部加密會導致整體加密的特點，故對遠場的節點分布律進行調整，改為均勻分布，這樣既保證噴管處網格質量，又保證遠場網格均勻分布。總網格數量11萬。

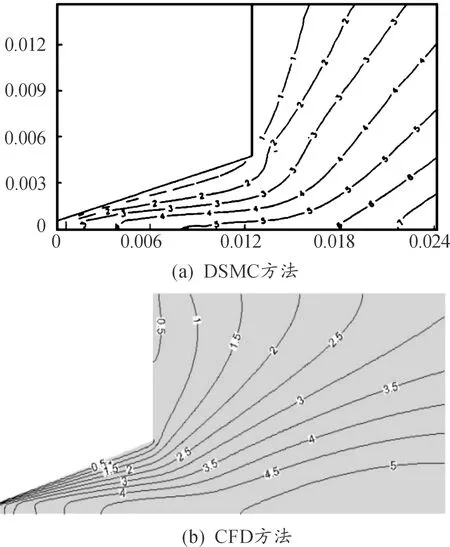
圖1 Ma數等值線圖

其中發動機噴管出口直徑36.3 mm，喉部直徑4.525 mm，出口直徑36.3 mm，幾何尺寸如圖2所示。室壓1.8 MPa，工作在120 km高度。由于120 km高度處已接近真空狀態，分子平均自由程已經接近或者很有可能超過噴管的幾何尺寸，因此要特別注意非連續效應的影響。

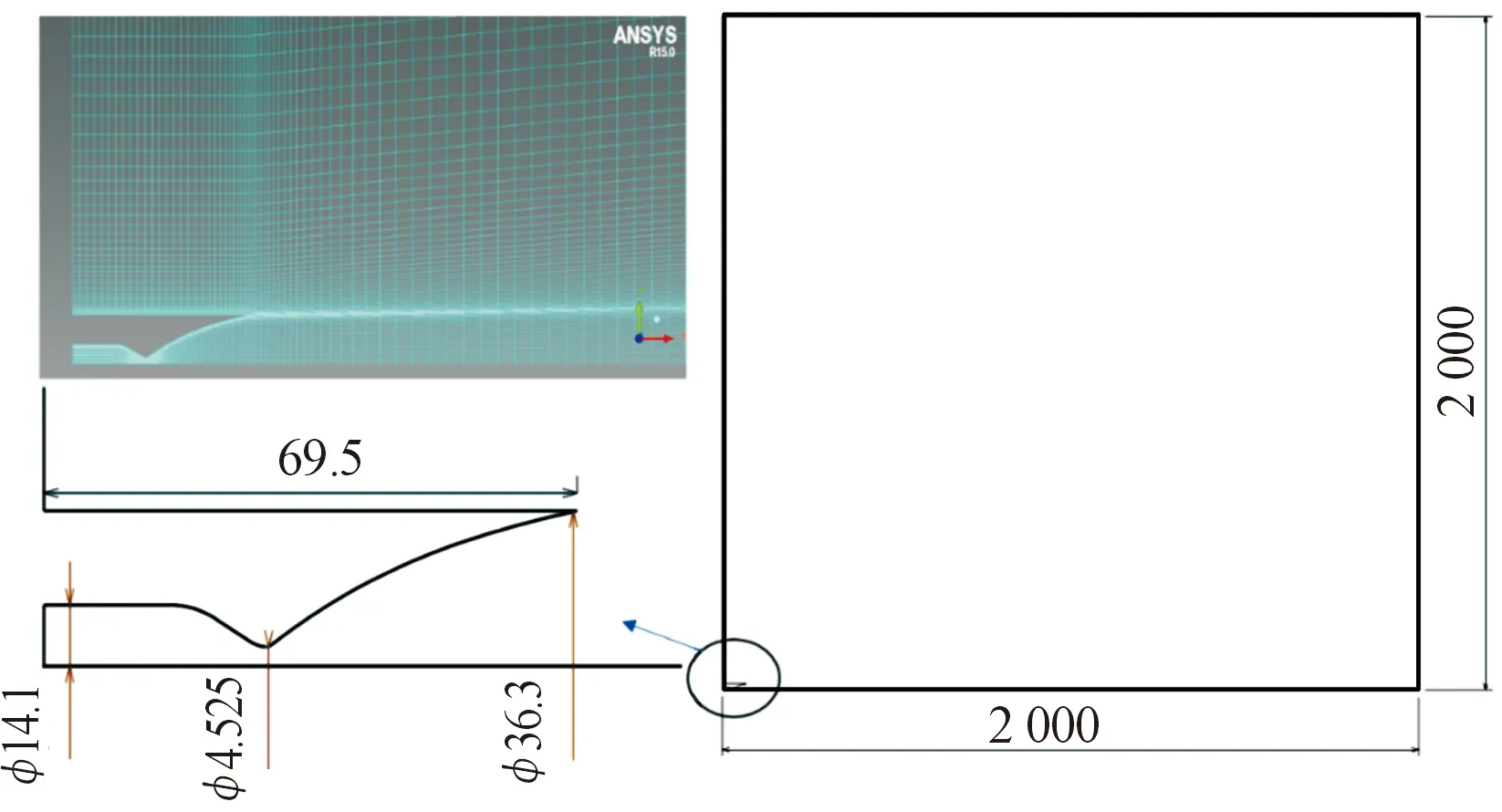
圖2 計算區域和噴管幾何構型

由于該噴管為軸對稱噴管，主要研究羽流狀態，并且計算中并未涉及到其他部件，因此整個計算域可以采用軸對稱構型以減小計算量。

其中燃燒室采用質量流率入口，給定流率、總溫、總壓、組份；遠場為壓力出口，給定壓力和組份；壁面均為無滑移壁面。

1.3 計算工況

表1給出了計算工況下推進劑的流量，燃料為CH6N2；氧化劑為N2O4。

在室壓為1.8 MPa條件下，根據室壓及燃料混合比，可以計算燃溫、燃燒產物等。采用平衡流假設，經過熱力學計算軟件CEA計算得到：燃燒室總溫3 103.7 K。以此作為計算的初始條件之一。

工作高度120 km情況下，經過查表得到：大氣壓力：0.002 54 Pa；溫度：360 K。

由于帶化學反應的計算需要耗費大量的計算資源，為了簡化計算，本次計算直接給定燃燒產物，而不考慮反應過程。

經過CEA軟件計算，反應主要涉及的產物有11種，分別為CO、CO2、H、HO2、H2、H2O、NO、N2、O、OH、O2。出于簡化計算的考慮，選取質量分數大于1%的組份，并對這些組份濃度進行歸一化處理，如表2。

表2 燃燒室組份濃度

3 計算結果

經過迭代計算，各項殘差變化趨于平穩，可以認為計算結果收斂。若僅從圖3所示的求解結果看，可以發現，氣體經噴管加速以后流出，在低壓條件下迅速擴張，達到了很高的Ma數。

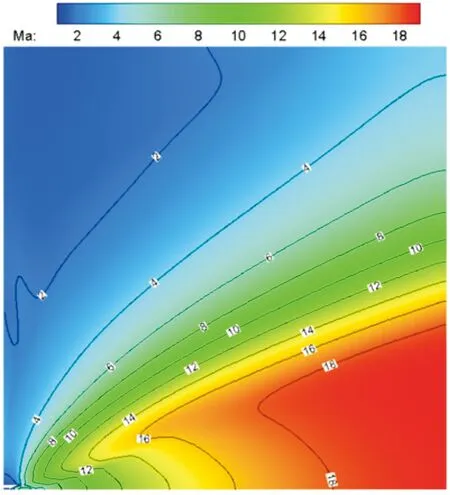
圖3 Ma數等值線圖

由圖4、圖5可以看到，相對于常壓條件，真空條件下尾流擴張角度更大，呈現出弓形擴張區域。同時，由于真空條件下極低的壓力，導致了垂直于流向方向上較大的擴散。可以看到，整個計算域的總溫均較高，這與常壓條件下完全不同。

圖4 整體流線圖

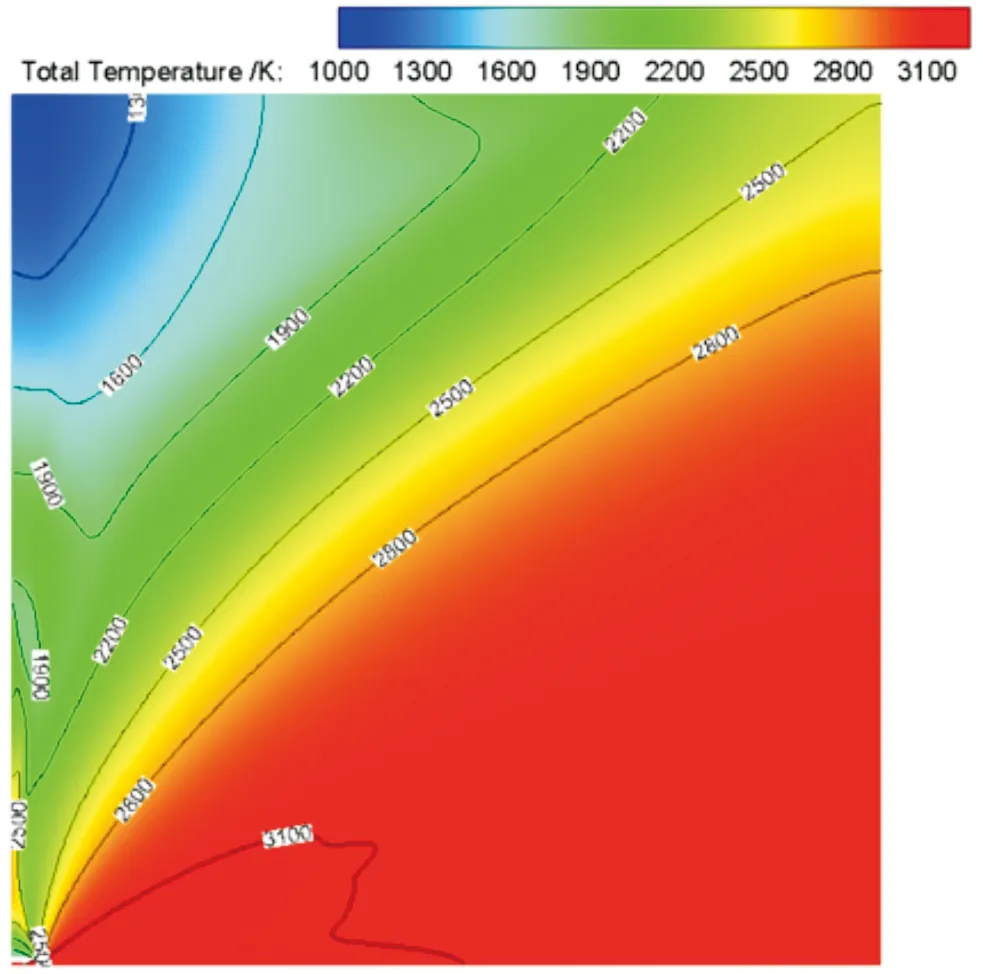
圖5 總溫分布等值線圖

圖6、圖7是噴管局部的Ma數、溫度分布云圖。可以看出在噴管出口形成較弱的斜激波，但波系結構和常壓條件下相比較少。

圖6 噴管附近Ma數云圖

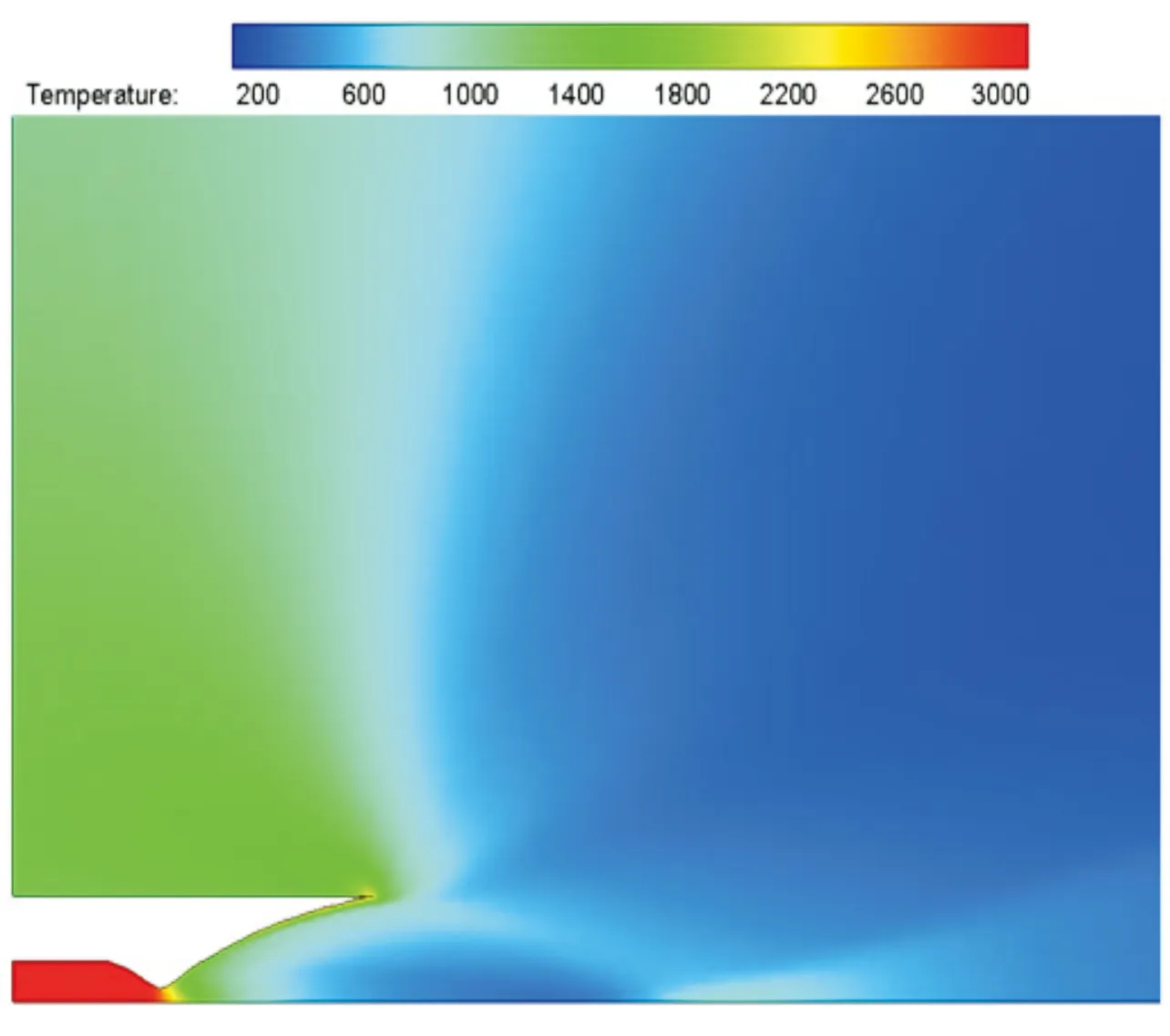
圖7 噴管附近溫度云圖

由于噴管附近的區域(不包括水平壁面上方的倒流區)分子數目較多，符合連續性假設，因此可以認為對該區域的求解結果真實度較高。而過渡流區以外的區域需要進一步探討。

4 結論

運用CFD方法來進行計算真空條件下拉伐爾噴管產生的羽流外邊界輻射特性對部件影響，可以得出真空條件下尾流擴張角度更大，呈現出弓形擴張區域。同時，由于真空條件下極低的壓力，導致了垂直于流向方向上較大的擴散。整個計算域的總溫均較高，這與常壓條件下完全不同。在噴管出口形成較弱的斜激波，波系結構和常壓條件下相比較少。

由于噴管附近的區域(不包括水平壁面上方的倒流區)分子數目較多，符合連續性假設，可以認為對該區域的求解結果真實度較高。