研究一棵樹，思考整座森林

賀麗珍/北京一零一中教師，北京海淀區數學骨干教師

數學在形成人的理性思維、科學精神和促進個人智力發展的過程中發揮著不可替代的作用。但數學教學不等于解題教學。數學教育的最終目標，不僅是使學生得到高分，更讓學生學會：用數學的眼光觀察世界，用數學的思維分析世界，用數學的語言表達世界。

學生是在教師的喚醒和激發下不斷發展、成長的，師生在生態課堂環境中，不斷地創造自我、發展生命。因此，我的教學觀是：通過研究一棵樹，思考整座森林。孤立知識點和問題的教學，好比一棵棵樹。為此，進行單元教學，通過研究一個個問題，來發現整體規律，讓學生整體把握課程內容和知識體系，從而把握數學內容的本質，思考“整座森林”。本文以高三函數綜合復習課為例，闡述如何“通過研究一棵樹，思考整座森林”。

教師心中有“森林”

首先，教師對問題涉及到的核心概念和知識邏輯要有深層次把握。教師要把握函數思想放在整個高中學段的地位，掌握函數與方程、不等式等內容的聯系，研究函數綜合問題解決的思維框架，即：基于函數概念，通過代數運算和函數圖象逐步深入地研究一類新函數的性質，從而解決問題。更要明確：解決函數綜合問題不在于解一道題，更是在于探究一類新函數的性質。

其次，教師整體設計“函數綜合問題”的單元教學（見圖1）。經歷問題引領、問題梳理、自主歸納三個層次，思維逐步提升。本節課（第6課時）是在問題梳理階段。

第三，教師把握學生思維障礙點，從而設計教學。經過“問題引領階段”的學習，總結學生思維障礙點：學生遇到函數綜合題還是機械求導，之后無從下手。原因是遇到方程、不等式問題，容易陷到暴力運算中，不能靈活地從函數、方程、不等式相互轉化的角度解決問題。因此本節課選取了這道題：

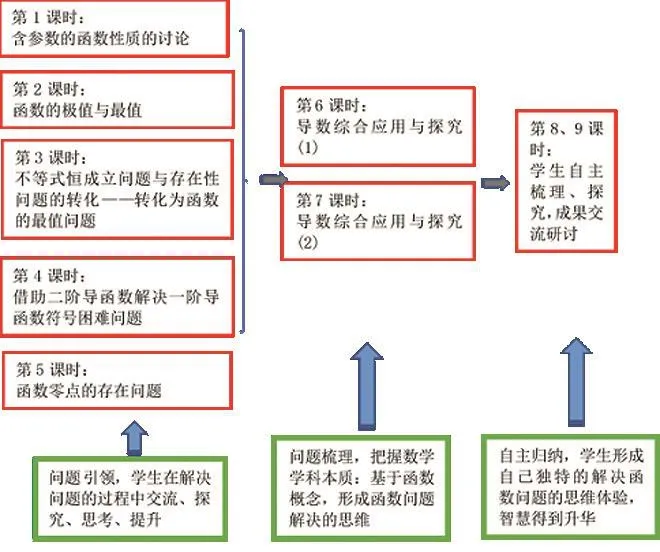
圖1

此問題綜合性較強，能充分暴露上述學生的思維障礙；這道題的實質是：研究方程有兩個不同實根的情況下，判斷兩個實根間距與的大小關系。可構建不同的函數從多種角度解決問題，但都是把不等式轉化為函數問題、把函數自變量的大小關系轉化為對應函數值的大小關系的比較，實質相同，都是基于對函數概念的理解，可以通過研究這道題，提煉解決函數綜合問題的思維方法；可基于本題提出創新性問題，讓學生進行創造、遷移。

通過研究一棵樹，思考整座森林

（一）基礎應用，開啟思維

（二）問題分解，思維突破

這個環節是整節課的核心，即“如何研究一棵樹”。首先分析條件：結合性質和直觀圖象，繼續深入研究方程兩個實數根以及的幾何和代數特征，分別用自然語言、圖形語言、符號語言來重述問題，不等式轉化為證明。學生提出證明方法，師生分析：需要借助函數的性質來研究，自變量的值的大小關系通過函數值的大小關系來比較.在同一單調區間內，問題轉化為比較。與的大小，即與的大小。

以上過程是“研究一棵樹”：基于學生已有基礎和思維障礙，邏輯連貫，難點突破，注重核心知識方法。接下來，教師鼓勵學生提出其他方法，并且對兩種方法進行分析。學生發現兩種方法雖然構造的函數不同，但本質都是通過恰當構造函數，把不等式問題轉化為“在同一個單調區間上通過比較函數值的大小得到自變量值的大小關系”。師生共同尋找解決函數問題一般方法，探究解決函數問題的思維框架。對于學生提出的其他方法，要給予充分肯定。因為學生的問題，反映了思維的多樣性，實現了“通過研究一棵樹，而思考了多棵樹”。

（三）創新探究，提升思維

圖2

（四）歸納總結，發展素養

這個階段是本節課的升華階段，即“通過研究一棵樹，到多棵樹，到整座森林”。師生共同探索函數綜合問題解決的思維框架（見圖2）：基于函數的概念，并以代數運算與函數圖象為手段，以及如何提出新問題并進行研究。函數圖象能夠直觀形象地表示出函數的變化狀態，邏輯推理和代數運算保證了嚴謹性。 學生掌握了研究“整座森林”的思維方法，反過來對于其他的“樹”，就可以了然于胸。

（五）自主歸納，創造自己的森林

本單元最后一個階段是學生自主歸納，建構自己的知識方法體系，創造自己的“森林”。

在復習過程中，我嘗試創新復習方法，讓學生原創、改編問題，創作自己的試卷，有的非常精彩，也有的是錯題，但都非常有價值。同學之間交流討論非常熱烈，收獲也很大。

《函數綜合復習》這一案例，從一道題的一個小問開始進行探討和研究，學生在經歷分析問題的結構、恰當構建函數、研究函數性質、解決問題的過程中，感悟研究函數問題的基本思維框架，從而讓學生學會整體把握函數的圖象和性質。教師引導學生繼續探究、總結、歸納和創造，注重培養學生發現問題、提出問題的能力。“通過研究一棵樹，去思考整座森林”就是這樣實現的，在此過程中，學生的直觀想象和邏輯推理素養得到充分的發展。

反思與改進

以上案例雖然在教學設計、錄課、說課方面均獲得了市、區級的獎勵，但我并不滿意。為什么學生到高三了還不能將不等式和函數問題靈活轉化？我進行了深刻反思：解決函數綜合問題的能力能不能在高一、高二的新授課階段就逐漸形成？在新一輪課堂教學中，我進行了改進和創新。

例如，在《不等式與不等關系》新課教學中，我的設計思想主要抓住“用函數的觀點看不等式”，即從新課開始學生就“通過研究一棵樹，思考整座森林”。

我將生活中的現象“加一勺糖，糖水更甜了”抽象為“糖水不等式”，并證明此不等式。接著，引導學生思考：“隨著糖的增加，糖水越甜”，實質上是判斷并證明函數的單調性。把“加糖糖水變甜”這個糖水不等式看作函數，把定量問題看作變量問題，用函數的觀點來解決問題。

學生進行深入思考，知識上承前啟后，方法上復習鞏固，思維上逐步提升，感受到函數與不等式的密切聯系，體驗數學發現和創造的過程，從而發展數學素養。反思我們的教學，基本的學科觀點、思維的發展應該在高一、高二新授課階段就應得以逐漸形成。