培養工科院校學生數學建模能力的大學數學教學的探索
——以《運籌學》教學為例
張 杰
(東北電力大學理學院,吉林吉林 132012)
數學是幾乎所有自然科學和工程技術研究的基礎,隨著科學技術的發展和計算機的普及,數學的應用領域越來越廣泛,以空前的廣度和深度向經濟、管理、金融、生物、醫學、環境、地質、人口、交通等新的領域滲透,數學理論與計算技術的不斷進步使得數學已經成為當代高科技的一個重要組成部分。大學數學教育在培養學生的創新意識和創新能力方面具有獨特的地位和難以替代的重要作用。人們對各種問題的要求越來越精確,使得數學的應用越來越廣泛和深入,數學理論與方法的不斷擴充。
在創新人才的培養過程中,需要改變數學教學的觀念,不僅需要學生掌握數學基礎知識,而且要有科技人才應具備的數學素質,即科學思維方法、邏輯推理能力、應用數學能力和計算機應用能力。通過這種教學使學生了解如何利用數學知識和方法去分析問題和解決問題,使他們在以后的工作中能經常性地想到用數學和利用計算機軟件去解決問題。在保持傳統數學教學優點的同時,融入討論式、問題式、案例式教學。使學生能在教師的指導下,選擇從自己周圍遇到的和社會生活中出現的有興趣的問題,用類似科學研究的方式去解決。這樣做法既有利于教師組織教學,也適合于教師引導學生對一些問題進行“研究”和“探索”訓練。這種探索有利于訓練學生發現問題的能力,鍛煉學生應用數學知識和方法及數學軟件解決問題的能力,有利于培養和發掘優秀人才。
1 算例分析
某染料廠用甲、乙、丙三種原料混合配制出A、B、C三種不同的產品。原料甲、乙、丙每天的最大供應量分別為100、100、60千克,每千克單價分別為65、25、35元。
由于A、B、C三種產品的質量限制,要求產品A中含原料甲不少于50%,含原料乙不超過25%;產品B中含原料甲不少于25%,含原料乙不超過50%;產品C的原料配比無限制,產品A、B含原料丙比例無限制。產品A、B、C每千克的售價分別為50、35、25元。
問應如何安排生產,才能使所獲利潤達到最大?
首先,將信息提煉并制表,可得問題的全部信息見表1。
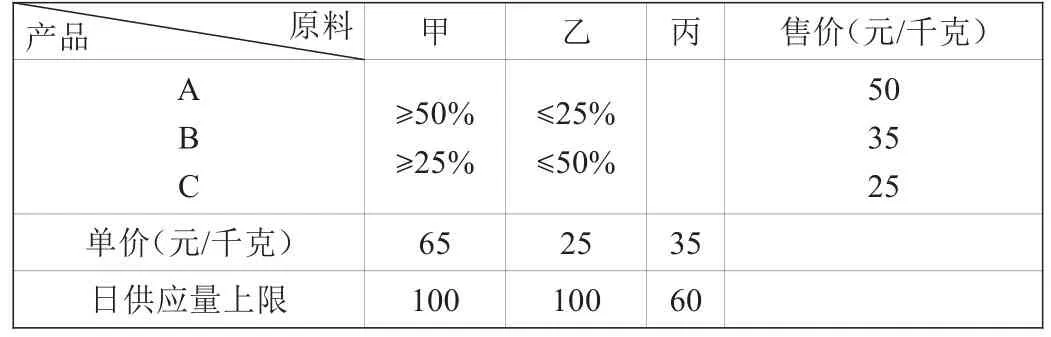
表1 產品信息表
(1)確定決策變量
設xij表示第i種產品中含第j種原料的數量(單位:千克),見表2

產品 原料乙甲丙A B C x11x12x13x21x22x 23 x31x32x33
(2)確定約束條件
原料配比約束:
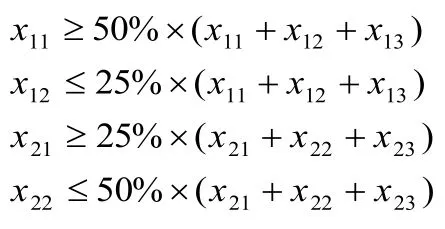
日供應量約束:
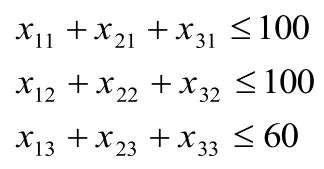
(3)確定目標函數
此問題的目標為獲利最大,因此目標函數為:
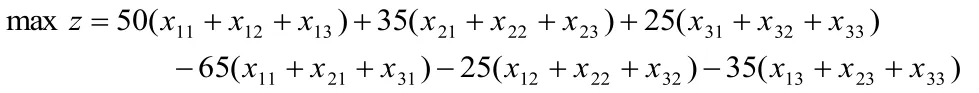
問題的數學模型為:
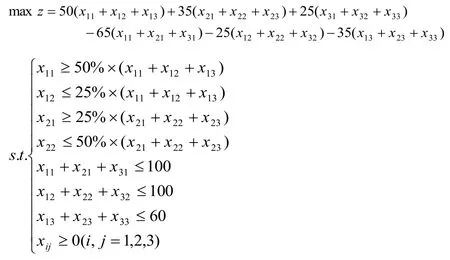
利用LINGO軟件求解,結果見下表
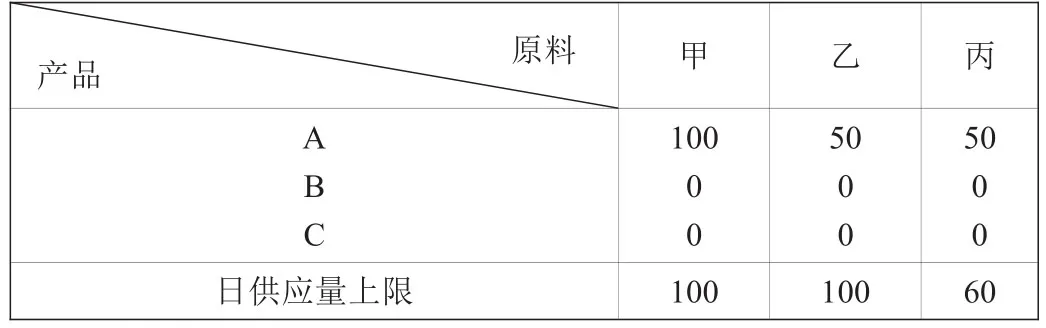
產品 原料甲乙丙A B C 100 50 50 0 0 0 0日供應量上限100 100 0 0 6 0
日獲利最大值為500元。
2 問題的進一步討論分析
2.1 產品最低售價的確定
進一步分析可知,原料過剩。在原有決策變量的基礎上,添加三個價格變量,設
產品A的售價為x1,產品B的售價為x2,產品C售價為x3,單位不變。
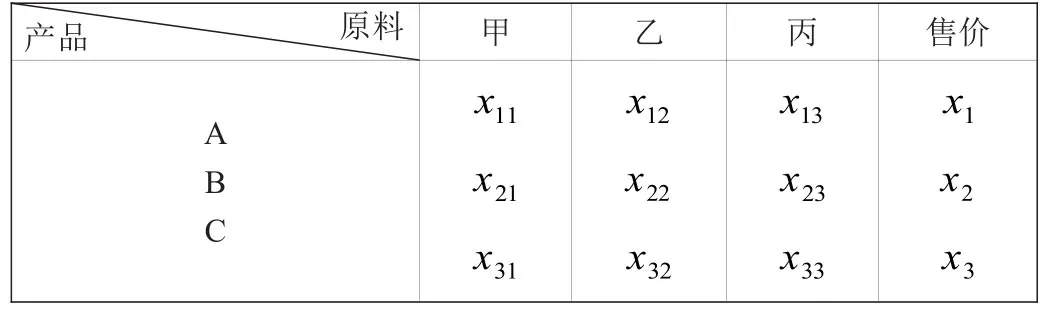
原料產品甲乙售價A B C x x 11 x13 x1 12 22 x 21 x x 23 x丙2 x31 x32 x33 x3
定價原則為:
(1)滿足產品配比限制;
(2)三種資源消耗完畢;
(3)每種產品的售價不低于其成本價。
即除原料配比約束外,增加兩個約束條件:
(1)三種資源消耗完畢:
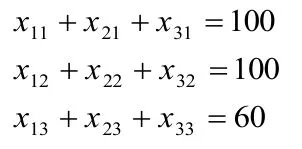
(2)售價不低于成本:
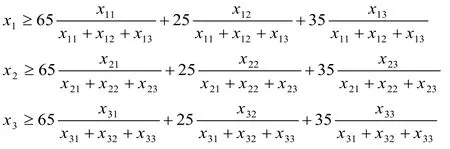
由于要確定三種產品的最低定價,因此目標函數為求利潤的最小值:
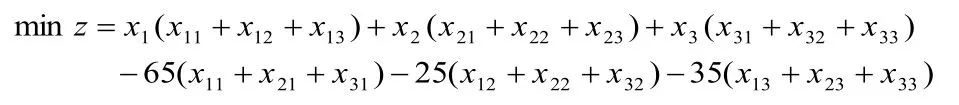
問題的數學模型為:

利用LINGO軟件求解,得
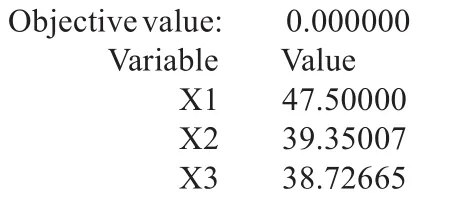
在滿足定價原則的前提下,最低定價為:產品A—48元,產品B—40元,產品C—39元,此時為零利潤。
2.2 最低定價下,原料消耗完畢的最大利潤
下面計算在最低定價下,原料消耗完畢時的最大利潤
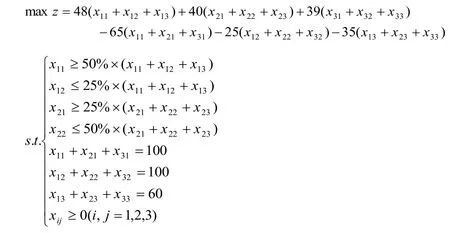
利用LINGO軟件求解,得


日獲利最大值:840元
日獲利最大值:840元。
2.3 產品售價增加對配比方案的影響
進一步分析產品售價增加對配比方案的影響,設
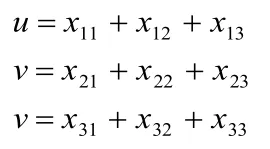
則問題的數學模型為:
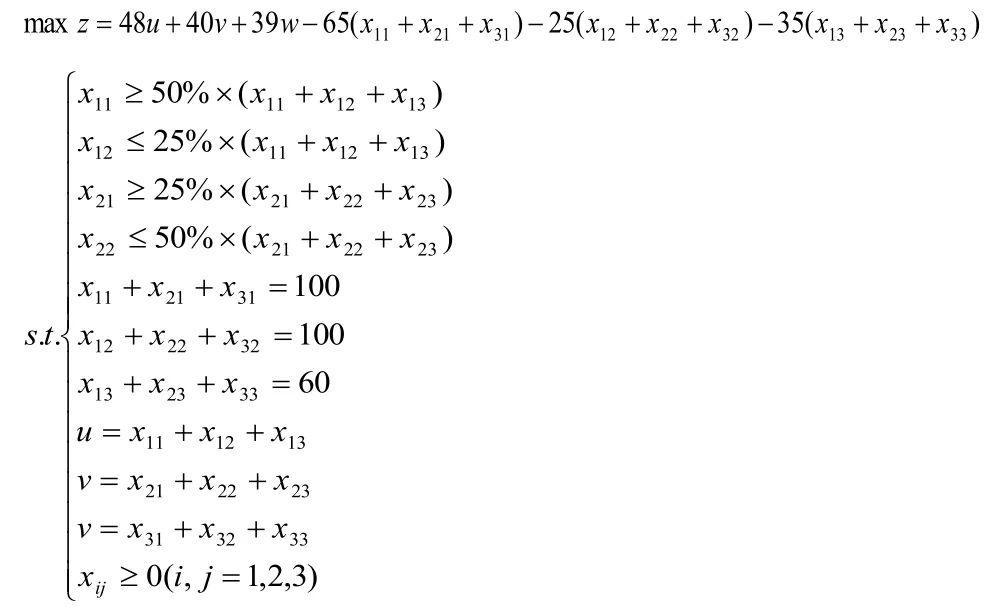
利用LINGO軟件對目標函數中變量u、v、w的系數進行靈敏度分析,結果如下:
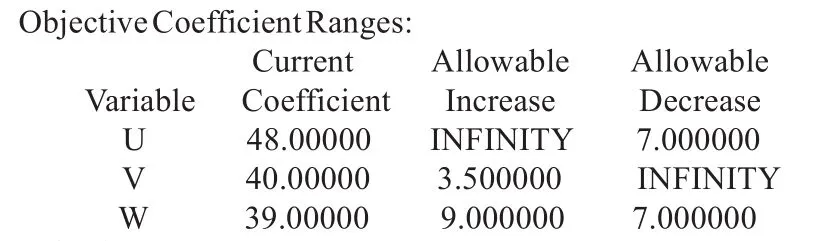
分析結果如下:
(1)產品A的售價增加對配比方案沒有影響;
(2)產品B的售價增加幅度不超過3.5元時,方案不變;
(3)產品C的售價增加幅度不超過9元時,方案不變。
對該案例的研究過程做如下總結:
(1)本案例在原有的條件下建模求解,其結果存在原料過剩以及利潤偏低的問題,原因是產品定價不合理造成的;
(2)在合理的定價原則下,建立產品定價模型并求解,得到了三種產品的最低定價;
(3)在最低定價下,重新求最大利潤,并且對產品售價的變化做靈敏度分析。
3 結論
解決實際問題過程中需要注意以下四點:
(1)在建立數學模型的時候盡量避免使用等式約束;
(2)對求解結果要給予解釋及合理性分析,逐步改進模型;
(3)對實際案例中繁雜的信息要善于提煉、列表;
(4)對于具有兩個腳標的決策變量,最好用表格的形式表示。

