迭代算法原理及其Python編程實現
黃旭
摘 要:迭代算法是數學算法在計算機中應用的一個熱點,也是計算機解決問題的一般思路,本文結合數學中二分法求根的原理,闡述了數學迭代算法的一般原理,并采用了Python加以實現,為進一步對數學算法理論和計算機的結合提供參考。
關鍵詞:迭代算法;二分法;Python;計算機程序
中圖分類號:TP31 文獻標識碼:A 文章編號:1671-2064(2019)18-0043-02
0 引言
求解方程的根不僅是在學校期間學習數學物理等學科的基本能力,更是今后從事科學研究、工程技術的基本技能。在現實應用中,方程通常都是基于物理原理建立的,不再是一些簡單的表達式,也就是說實際中的求解問題十分復雜,有的甚至沒有固定的求解方法。幸運的是,現在很多的問題都可以運用計算機進行求解,計算機除了會利用已有的公式求解之外,還擅長采用逐步迭代的方法得到近似解,這對科學研究與工程應用具有十分重要的作用[1]-[2]。
本文主要基于高中數學中對連續函數的根存在性角度出發,通過查找資料,可以采用較為簡單的二分迭代算法去逼近真實根,就迭代算法進行了系統性的概括,并利用Python語言對一般的二分迭代算法進行了實現。
1 迭代算法原理分析
1.1 迭代算法概況
迭代算法[3]-[4]在平常計算的時候用的非常之多,但是以前用迭代算法求解方程的時候特別復雜。而隨著計算機技術的發展,利用計算機進行迭代算法的計算速度很快,只需簡單的命令即可讓該算法不停地迭代,直到結果符合條件。這也就使得人們從繁雜的計算中解放出來。因此,目前迭代算法的使用也逐漸的增多,甚至成為最基本的一種方法。實際上,迭代算法的原理較為簡單,它最主要的就是進行關系式的迭代。其基本含義為:不斷地用求解出來的量去計算新的數值,直到最后的數值滿足所求解的方程式,即停止迭代。
迭代算法一般用于求解最優化問題。它能夠反復的迭代,直到最符合的那個值出現,并停止繼續計算。在求解優化問題的時候,迭代算法會有一定的局限性。一是,最終的結果只是局部的最優解,并不是全局最優。二是,求解會陷入一個死循環。出現第一種原因的情況可能是在某個范圍內該數值就是最優的,這個時候計算器就會斷定這個數值就是方程式所需要的,即停止計算。這時候就需要設置好計算時的范圍,盡可能的讓計算機迭代多次,對所求的結果進行對比。出現第二種情況的原因是在給定的關系式以及數值范圍內求不出符合最優解,計算機將會不停地迭代。
因此,我們在用迭代算法進行計算的時候需要注意這幾點:首先要仔細的確認迭代變量的數值;其次是對迭代的次數進行設置,不能讓該算法進入到死循環;再者在必要的情況下應盡量用較少的關系式去表示你的問題,減少計算器的運行量,因為計算器的運行內存也是有限制的,否則會出現程序終止的情況。
目前,迭代算法的類型非常多。例如:牛頓迭代算法、迭代最近點算法、二分法迭代算法等。本文主要對二分法迭代算法進行分析,利用簡單的二分迭代算法求解方程,并且對二分迭代算法的實現進行了詳細的闡述。
1.2 二分法原理剖析
二分法顧名思義,就是將某個數值一分為二。通常情況下,數據量較大的時候適合使用二分法進行計算。但需要注意的是,利用二分法求解的數據必須單調增或減并且不能有重復的數值。二分法基本思路為,先將數據排序(升或者降序都可以)對于給定的數據序列,從數據序列的中間進行拆分,拆分為前半部分和后半部分。如果當前拆分的數值是滿足所有條件的值,那么可以停止拆分數據序列;如果當前拆分的數值不是滿足的值,再判斷是否小于拆分之后序列的后半段。如果是,則從前半部分數據序列中繼續查找,否則從后半部分數據序列中繼續查找。一直進行數據的拆分,直到找到滿足所有條件的。其二分法基本思路定義用數學式子表達為:
比方說,假設,二分法的步驟就是將區間不斷地進行拆分。
(1)將區間表示為區間,其中當時,則有。
(2)對于設,等于或者,其中表示區間的中點。
從上述二分法的定義中可以看出,它能夠很好地將計算步驟不斷地減半,極大的提高了運算速度和效率。
2 二分法的Python實現
2.1 二分法求解根式
在我們求解方程的時候,通常會利用現有的公式進行求解,即求根公式。但實際上,求根公式并不是對所有的方程都能適用,并且不一定求出來的結果正好就是精確的數值。很多時候求出來的結果都帶有根式,這個時候想求解精確的數值解幾乎是不可能的,而在某些情況下,必須要求求出某一精確數值。那么我們就需要求解一個近似值用于代替根式的值。求解某一數值的根式方法有二分法和牛頓法。
接下來本文主要對二分法求解根式進行詳細的敘述。其基本求解原理就是不斷地對求解的根式進行數值范圍的縮小,直到能夠找到所求根式能收斂某個數,即停止縮小范圍,輸出近似解。
本文先對二分法求解平方根進行分析,然后再運用到多次根式當中。二分法求解根式的具體步驟為:
(1)通過計算方程得出,求出其近似的數值解;
(2)令,求得,將與進行比較;
(3)情況1:當的時候,則記當前近似解區間的上限為。則繼續向下進行數值取半,即。在重復步驟2,直到,得到近似解的下限為。此時近似解的區間為,即最終的近似解一定在該區間之內。然后再從該區間內繼續按照步驟2進行取值,直到逐漸收斂至為止;
(4)情況2:當的時候,則記當前近似解區間的下限為。則繼續向上進行數值取半,即。然后繼續重復步驟2,直到,得到近似解的上限為。此時近似解的區間為,即最終的近似解一定在該區間之內。然后再從該區間內繼續按照步驟2進行取值,直到逐漸收斂至為止。
案例1:求的近似解。
第一步,先取,求得,此時,求得區間上限為;
第二步,繼續向下取值,令,此時,此時區間下限為;
第三步,令,此時,此時區間下限為;
第四步,重復第三步,重新取值,直到無限接近5,則值即為我們要求的根式值。
根據上述例子可以發現,如果使用手動進行計算,還是具有一定的復雜程度的。本文將利用Python軟件[5]對二分法求解根式進行編程,實現計算機自動計算根式的解。
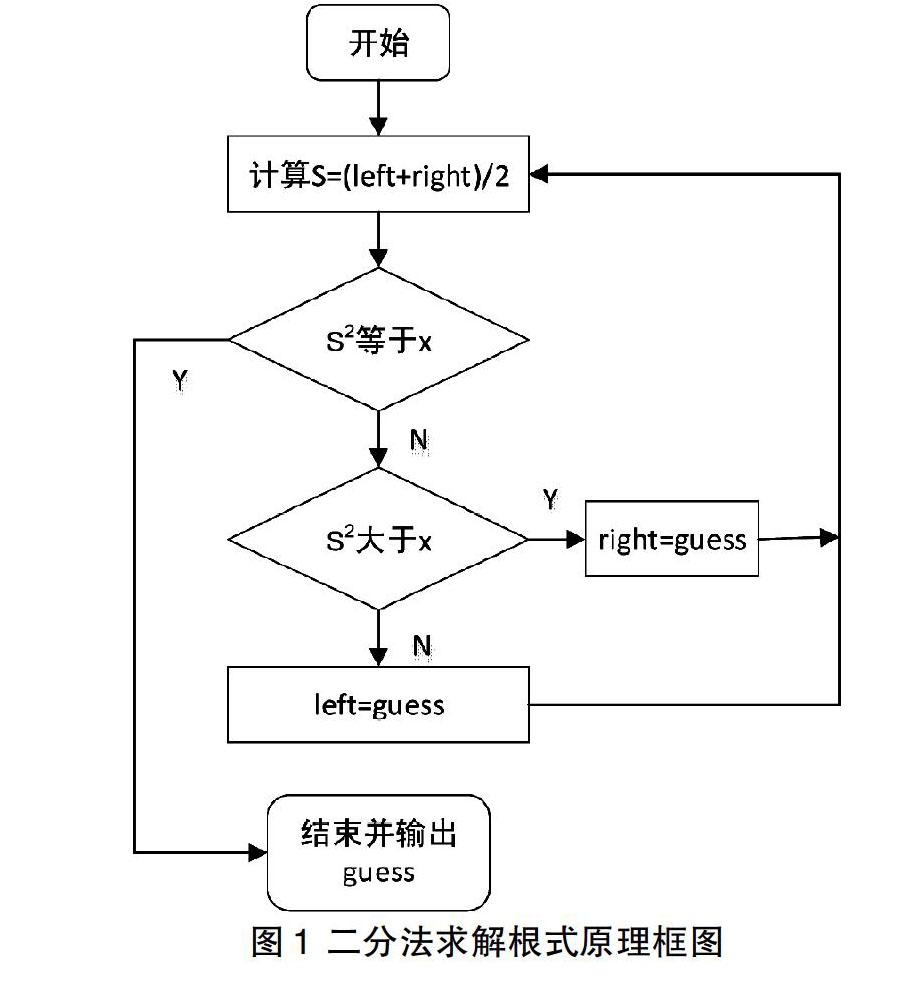
首先對二分法求解根式的基本思路進行轉化。其基本思路框圖1所示。
初始化:為所求根式;left為近似解區間的左區間值;right為近似解區間的右區間值。
根據該框圖寫出案例1的Python代碼為:
Num=5
x=sqrt(Num)
x1=num/2
left=0
right=Num*1
count=1
while abs(x1-x)>0.00000001:
print count,x1
count+=1
if(x1**2>Num):
right=x
x=left+(x1-left)/2
else:
left=x1
x1=right-(right-x1)/2
return y
print(sqrt(5))
另一種求解根式的方法是牛頓法,它是17世紀被提出來的,主要是用來求解近似值。該方法主要是利用單根附近有平方收斂的原理,來進行計算根式的近似值的。其牛頓迭代的公式為。在兩種求解根式的方法中,二分法迭代次數要多于牛頓法。
2.2 二分法求解方程
在平常求解方程組的過程中,我們會遇到無法用求根公式得出方程的解,就必須按照一般解方程組的步驟求出方程的解。但是遇到比較復雜的方程式,手動解方程是一件非常耗費時間的事情,且結果不一定準確。本文介紹使用二分法來求解方程,最后給出用Python求解的具體思路。
本文先介紹用二分法求解函數的基本定義,在使用二分法求解方程的時候,需要注意幾個條件,將求解的方程用函數的形式表達出來,則有函數在區間上為單調且連續的函數,同時滿足,滿足這幾個條件的函數才能使用二分法進行求解。其具體求解思路如下:
步驟1,給定一個誤差,即認為求出的解在誤差多少的范圍能是能被接受的;
步驟2,先求出區間的中點值,記為;
步驟3,將令,計算出的值;
步驟4,假設求出的的值為零,那么就是函數的零點,即使方程的解;如果,則需要進一步的判斷:若,則令;若,則令;
步驟5,若,則可以認為方程的解等于或者。如果,則繼續重復步驟2到步驟4。
實際上,該方法主要是在縮小方程解所在的區間,直到左右兩區間的值無限接近,即認為左右兩區間相等,且為方程的解。值得注意的是,用二分法求解方程,只能求出方程的一個單根。
案例2:求解。
根據二分法求方程解的步驟:
步驟1,給定一個誤差;
步驟2,先求出區間的中點值,記為;
步驟3,將令,計算出。
由于,且,因此令。此時方程的解區間變為,然后繼續重復步驟2到步驟4。直到,即停止計算。由于手工計算過于復雜,且計算時間慢。本文給出二分法求解方程的Python代碼。其一般代碼如下:
a,b,c,d=input().split()
m,n=input().split()
m=float(m)
n=float(n)
a=float(a)
b=float(b)
c=float(c)
d=float(d)
def f(x):
return a*pow(x,3)+b*pow(x,2)+c*x+d
def erfen(m,n):
if((n-m)<0.0001):
print(“{:.2f}”.format((m+n)/2))
elif(f(m)*f(n)<0):
if(f((m+n)/2)==0):
print(“{:.2f}”.format((m+n)/2))
else:
if(f((m+n)/2)*f(m)>0):
m=(m+n)/2
erfen(m,n)
elif(f((m+n)/2)*f(n)>0):
n=(m+n)/2
erfen(m,n)
if(m erfen(m,n) elif(m==n): print(“{:.2f}”.format(m)) 根據案例和程序,得出a=0,b=1,c=-11,d=10,m=-15,n=20。在運行上述程序之后,只需要在窗口輸入: 0 1 -11 10 -15 20 即可得到最終結果為10.00。 3 結語 從本文給出例子的求解過程和求解結果中可以看出,通過二分法求方程的解,有且只有一個單根。但實際上,案例中的方程有兩個解:1和10。并且在求解過程中解區間的取值也應該十分的注意,因為是隨機取值,這就會導致方程的解不在該解區間內,最終導致求解方程組失敗。因此,在用二分法求方程時,應該盡可能的將解區間的范圍擴大,以免求解失敗。另外,當給定的誤差的值越小時,最終結果會越準確。 參考文獻 [1] 張曉勇,王仲君.二分法和牛頓迭代法求解非線性方程的比較及應用[J].教育教學論壇,2013(25):139. [2] 吳梨娟.信息技術下二分法求解函數的零點個數探討[J].高中數理化,2013(8):10-11. [3] 林永,陳浩.用二分法求解一元實系數多項式方程的全部實根[J].大學數學,2008,24(4):88-90. [4] 隋麗娜.利用高級語言實現數學中的二分法[J].人力資源管理,2010(6):186. [5] 王登岳,張宏偉.基于Python求解偏微分方程的有限差分法[J].計算機時代,2016(11):14-16.

