原子核等勢能面的Matlab繪制

上海電機學院文理學院 上海 201306

摘 要：利用Matlab軟件的griddata函數對平均場方法獲取的原子核的勢能面進行了插值平滑，通過繪制等高線，得到等勢能面，并以核素74Ge等勢能面的繪制為例，分析了74Ge的形變。

關鍵詞：原子核;等勢能面;Matlab

中圖分類號：O571.21

繪制原子核的等勢能面是分析核素形變的重要的手段。從系統的哈密頓量出發，利用受限的Hartree-Fock方法，[1]可以計算β自由度（描述原子核的軸對稱形變）和γ自由度（描述原子核的三軸形變）下的勢能。由于計算的核勢能是散點圖，還需通過數值方法對散點進行插值計算，得到光滑的勢能面，并在β-γ極坐標平面上通過繪制等高線得到等勢能面，從而進一步判斷原子核的形變情況。

Matlab作為一個具有較強功能的科學計算軟件，能夠直接調用數值方法的計算程序，可以快速高效地實現各種數值計算過程。本文將利用Matlab軟件中的griddata函數對離散的原子核勢能進行插值平滑，具體說明Matlab軟件在原子核等勢能面繪制中的應用。

1 griddata函數簡介

Matlab的griddata函數可以對散點數據進行兩維和三維插值。以兩維插值為例，其命令語法如下：

zq= griddata（x，y，z，xq，yq，method）

上述命令可以實現將（x，y，z）的散點數據平滑成z=f（x，y）形式的曲面，在（xq，yq）指定的查詢點進行插值，并返回插入的值zq，其中xq和yq為兩維查詢點網格，zq則為兩維數組。method為插值方法，可以選擇linear、nearest、natural、cubic、linear 或 v4，其中前四個選項是基于三角剖分的插值方法，而 v4則為雙調和樣條插值方法，默認方法為linear。本文中，我們采用cubic選項，即基于三角剖分的三次插值方法。griddata函數的詳細語法說明可見Matlab軟件的幫助文件。

下面我們利用griddata函數來繪制核素74Ge的等勢能面。

2 核素74Ge等勢能面繪制

在原子核的殼模型中，以核素56Ni為不活躍的殼芯，74Ge的價核子可以在pf5/2g9/2的模型空間中被激發。利用受限的Hartree-Fock方法，通過JUN45有效相互作用，我們計算了β和γ自由度下，體系總角動量為0時，74Ge的勢能。相關的計算方法參見文獻[2]的討論，這里不再贅述。計算得到的勢能分布可見圖（a）中的散點。利用griddata函數可對散點進行插值平滑，再進一步地將平滑后的勢能面投影到β-γ極坐標平面上，就可以做出等勢能面圖。具體的計算過程見下文的Matlab程序代碼和對應的注釋：

r=load（'fort.30'）;%讀取計算的離散的核勢能

subplot（2，1，1）;

plot3（r（：，1），r（：，2），r（：，3），'r.'）;%繪制勢能的三維散點圖

xlabel（'＼＼it x'）; % x=β

ylabel（'＼＼it y'）; % y=β *sin γ

zlabel（'{＼＼it E}（MeV）'）; %E為勢能

title（'（a）'）; hold on;

xlin=linspace（min（r（：，1）），max（r（：，1）），800）;

ylin=linspace（min（r（：，2）），max（r（：，2）），800）;

[X，Y]=meshgrid（xlin，ylin）; %將插值計算的區域網格化

Z=griddata（r（：，1），r（：，2），r（：，3），X，Y，'cubic'）; %利用griddata函數插值平滑離散點，并在網格化的查詢點[X，Y]上，返回插入的值Z

mesh（X，Y，Z）; %繪制平滑后的勢能面

grid on;box on;

subplot（2，1，2）;

contourf（X，Y，Z，12）; %將勢能面投影到β-γ極坐標平面上，繪制等高線，得到等勢能面

title（'（b）'）;h=colorbar;

set（get（h，'Title'），'string'，'{＼＼it E}（MeV）'）;hold on;

sector（0，0，0，60，0.25）; % 利用自定義的函數sector 繪制β-γ平面極坐標

function sector（x0，y0，angle1，angle2，R） %定義sector函數

t=linspace（angle1/180*pi，angle2/180*pi，1000）;

x=R*cos（t）;y=R*sin（t）;x（1001）=0;y（1001）=0;

plot（x，y，'k-'）;axis（[x0，x0+R，y0，y0+R]）;

set（gca，'YColor'，'white'）;box off;

x1=R*cos（30/180*pi）;y1=0.01+R*sin（30/180*pi）;

x2=R*cos（60/180*pi）;y2=0.01+R*sin（60/180*pi）;

xlabel（{'＼＼it ＼＼beta'}）;text（x1，y1，'{＼＼it ＼＼gamma}=30^{＼＼circ}'）;

text（x2，y2，'60^{＼＼circ}'）;text（R，0，'0^{＼＼circ}'）;

end

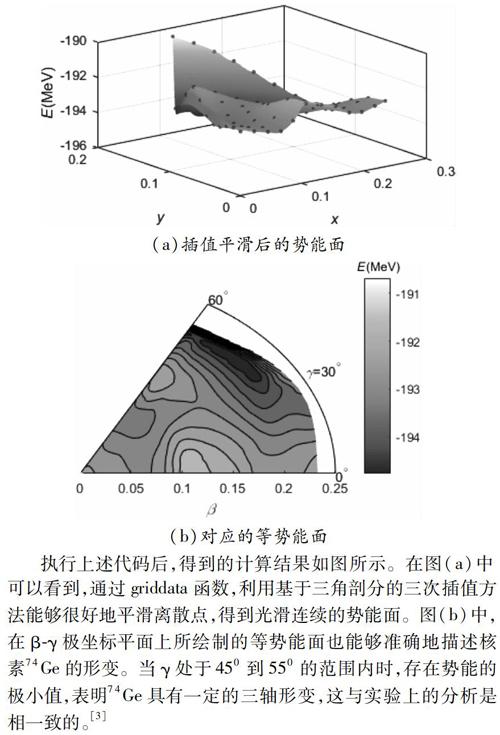
（a）插值平滑后的勢能面

（b）對應的等勢能面

執行上述代碼后，得到的計算結果如圖所示。在圖（a）中可以看到，通過griddata函數，利用基于三角剖分的三次插值方法能夠很好地平滑離散點，得到光滑連續的勢能面。圖（b）中，在β-γ極坐標平面上所繪制的等勢能面也能夠準確地描述核素74Ge的形變。當γ處于450到550的范圍內時，存在勢能的極小值，表明74Ge具有一定的三軸形變，這與實驗上的分析是相一致的。[3]

3 結語

利用Matlab軟件的griddata函數對受限的Hartree-Fock方法計算得到的核素74Ge的離散的勢能面進行了基于三角剖分的三次插值平滑，繪制的等勢能面能夠很好地反映出74Ge的結構特征。由于Matlab語言編寫簡單，函數功能豐富，本文提供的方法不失為繪制原子核等勢能面的一種有效途徑。

參考文獻：

[1]RING P，SCHUCK P.The Nuclear Many-Body Problem[M].New York：Spring-Verlag，1980：266.

[2]金華.76Ge 形變的殼模型分析.上海電機學院學報[J].2017，20（5）：301-305.

[3]SUN J J，SHI Z，LI X Q，et al.Spectroscopy of 74Ge：From soft to rigid triaxiality[J].Physics Letters B，2014，734：308-313.

作者簡介：金華（1979-），男，上海電機學院教師，主要從事物理學的教學與研究工作。