基于緊湊拉伸試驗的含缺陷燃氣管疲勞壽命預測分析*

呂彥偉，劉欽節,2，付 強，袁宏永，付 明

(1.安徽理工大學 能源與安全學院，安徽 淮南 232001；2.深部煤礦采動響應與災害防控國家重點實驗室，安徽 淮南 232001；3.清華大學 合肥公共安全研究院，安徽 合肥 320601)

0 引言

隨著天然氣的使用規模越來越大，國內各地有關燃氣管道的破壞事故時有發生。引發此類事故的原因眾多，其中含初始缺陷管道的疲勞破壞是其主要原因之一[1]。管道在實際工作期間的輸氣量不穩定，且存在一定范圍內的壓力波動，對于含初始缺陷的燃氣管道，此缺陷周圍易產生較大的應力集中，管道更易在缺陷處出現裂紋擴展。當裂紋擴展至臨界失穩尺寸時，管道產生疲勞斷裂，最終導致泄漏。因此，分析燃氣管泄漏發生的原因，預測燃氣管疲勞壽命，對管道的日常維護管理以及制定相應措施具有重要意義。

鑒于此，鐘勇等[2]利用理論推導壽命與實測結果對比的方法，驗證不同應力強度因子下裂紋擴展速率與疲勞壽命的關系；蔣云等[3]對含缺陷管道疲勞壽命進行理論推導，得到預測管道壽命的方法；吳冰等[4]通過TC17合金材料進行疲勞裂紋擴展速率試驗，結合裂紋容限相關理論，估算疲勞剩余壽命；邱保文等[5]采用基于失效評定圖技術對油氣管道的疲勞壽命進行計算和分析，并通過對比全尺寸實驗結果驗證計算的可靠性；馬秋榮等[6]基于小試樣疲勞實驗分析，得出X60和X80管道在不同應力比下的疲勞裂紋擴展規律，并對X80含裂紋管道的疲勞壽命進行預測；余建星等[7]采用理論計算和數值模擬方法分析裂紋各種參數對海底管道疲勞壽命的影響作用。

綜上所述，國內外學者對預測含缺陷管道壽命開展了大量研究，但鮮有利用裂紋擴展速率實驗結合理論推導對工程實踐條件下含缺陷燃氣管道壽命進行預測和研究。本文擬利用斷裂力學中的損傷容限分析方法推導含缺陷燃氣管疲勞壽命預測模型，利用MTS電液伺服疲勞試驗機開展疲勞裂紋擴展速率試驗研究，分析含初始裂紋管道在交變壓力作用下的裂紋擴展規律，為預測分析燃氣管疲勞壽命、監測管道破壞過程及制定相應措施提供參考。

1 含缺陷管道疲勞壽命預測的理論模型

對于含有裂紋的燃氣管道，在交變壓力作用下，其壽命由裂紋擴展行為所決定。若外加應力水平較低、裂紋尺寸較小，相應的應力強度因子低于應力強度因子門檻值ΔKth時，裂紋不會擴展；反之亦然。因此，裂紋的擴展速率決定管道的使用壽命，而應力強度因子是評判含裂紋構件是否斷裂及裂紋擴展速率的重要參量[8]。對于恒定幅值載荷，可以采用斷裂力學中損傷容限分析法，通過積分裂紋擴展速率表達式預測管道的使用壽命。

國內外學者常用Paris公式研究裂紋擴展速率與壽命N的關系，其表達式為[9]：

da/dN=C(ΔK)m

(1)

式中：N為裂紋擴展到臨界尺寸時的循環次數，cycle；da/dN為裂紋擴展速率，即每個循環下裂紋擴展量，mm·C-1；C，m為Paris的2個重要參數；ΔK為裂紋尖端應力強度因子。

管道泄漏多數是由于疲勞斷裂造成的，其中最常見最危險的初始裂紋即為張開型裂紋(Ⅰ型裂紋)，其主要表現為在壓力的波動下，裂紋沿深度方向非穩定性擴展。為模擬實際管道中的泄漏情況,以表面缺陷裂紋最終擴展為穿透裂紋作為壽命結束的依據,即以管厚作為管道失穩的臨界尺寸。現對管道上表面裂紋尖端的應力強度因子進行分析。

在1個壁厚為ac的管道表面上存在1個沿管道軸向方向的未穿透的半橢圓形表面裂紋,裂紋長軸和短軸分別為2a和2b。管道內壓為p，該處的應力強度因子計算式為[2]：

(2)

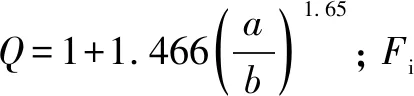
僅考慮在裂紋最深處(θ=π/2)的應力強度因子為：

(3)

式中：KI深為在管壁上I型裂紋最深處的應力強度因子。

在一定交變工作壓力下，裂紋最深處的應力強度因子：

(4)

將式(4)代入式(1)式，得：

(5)

在管道實際運行中，由于受到內壓的循環加載作用，裂紋會沿徑向擴展直至貫通，形成泄漏，造成破壞。所以，將式(5)用于表面裂紋沿深度方向的擴展時,應對其進行修正。蔡強康等[11]通過研究表明，裂紋沿軸向擴展量大致是沿徑向擴展量的1.384倍。

令U=1.384,修正后表面半橢圓裂紋的徑向擴展速率為：

(6)

對式(6)進行積分得：

(7)

綜合疲勞裂紋擴展速率公式da/dN-ΔK及半橢圓表面裂紋的尖端應力強度因子的方程,可得循環周次計算公式為：

(8)

通過分析可以得出，參數C和m、燃氣管中的內壓變化值Δp、疲勞裂紋容限尺寸ac以及初始裂紋尺寸a0對工程實踐中燃氣管疲勞壽命N有重要影響作用。

2試驗材料與方法

2.1 試驗設計

試樣取自于安徽淮南天然氣二氣源管道工程，管徑為DN400，設計能力4 萬m3/h，年輸氣能力為3.15億m3。試樣的材料基本力學性能參數見表1,按照GB/T6398—2017《金屬材料疲勞裂紋擴展速率試驗方法》[12](以下簡稱“標準”)，采用寬度W=50 mm，厚度B=12.5 mm，機加工缺口長度an=6 mm的標準緊湊拉伸CT試樣，如圖1所示。試樣缺口通過線切割加工而成，預制的裂紋由熱處理后再進行線加工而成。

表1 管材力學性能表Table 1 Mechanical properties of pipeline material

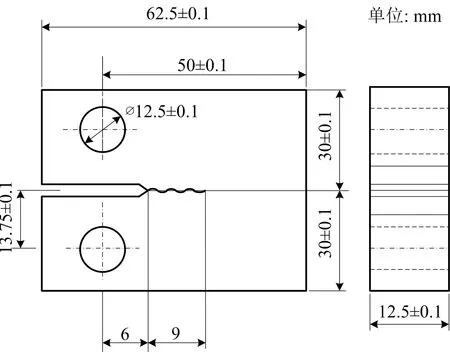
圖1 標準CT緊湊試樣Fig.1 Standard CT compact sample

2.2 試驗過程

試驗采用“標準”中推薦的U型夾具，在MTS電液伺服疲勞試驗機上進行試驗測試，如圖2所示。利用MTS-810試驗系統自動記錄加載載荷及循環次數。試驗所加載荷頻率為10 Hz，波形為正弦波,應力比R=0.1。

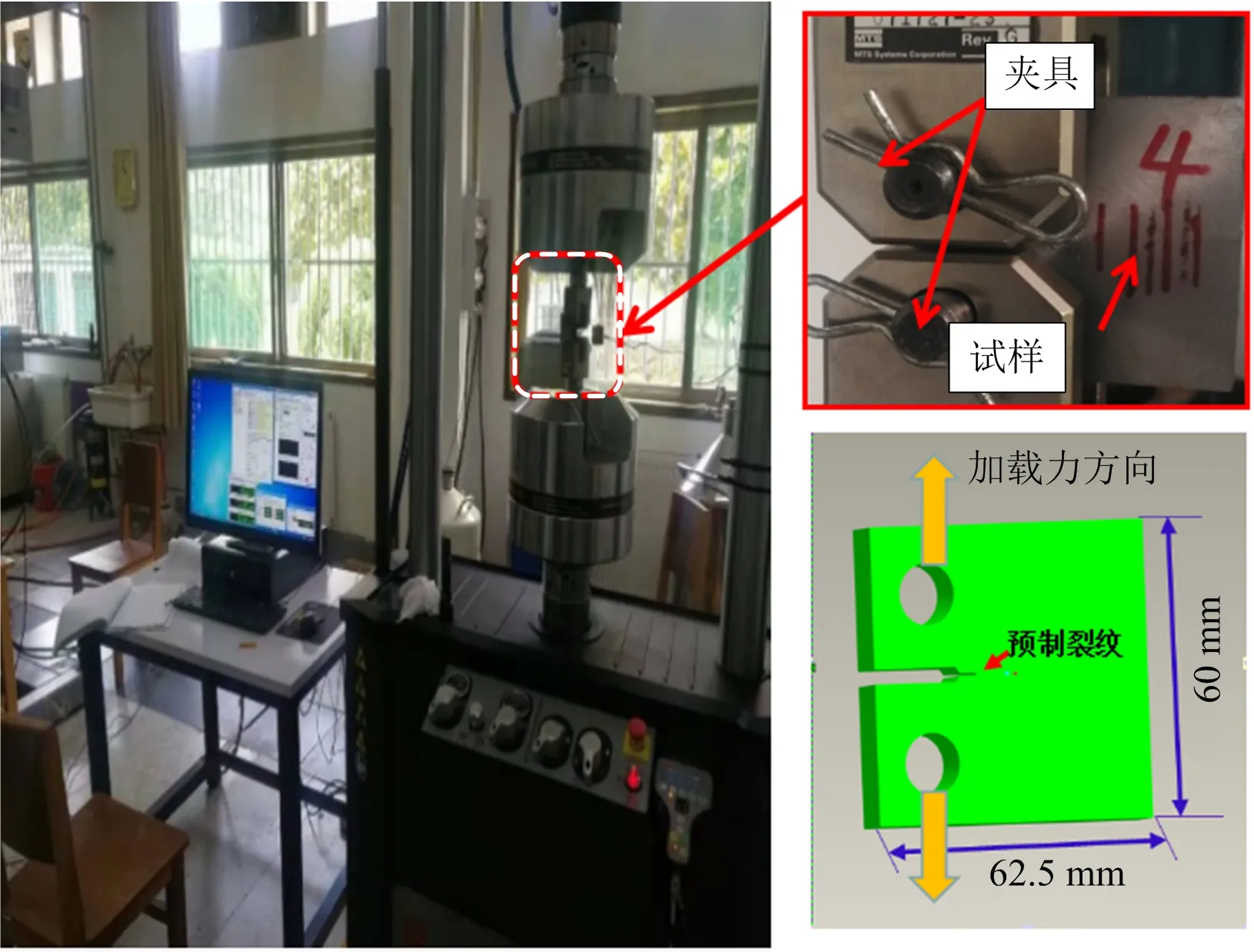
圖2 MTS-810系統裝置圖及試樣示意Fig.2 MTS-810 system device and sample schematic

具體試驗過程如下：

1)按照“標準”中的相關規定計算得出各試件的預制力，并將其加載到試驗系統預制出長度為9 mm的裂紋；

2)在室溫、空氣環境中，分別采用4種不同的載荷(14.4，19.53，22.32，25.11 kN)進行疲勞試驗，試驗過程中保持恒定的交變載荷幅值Δp。

3)利用高清數碼相機拍照記錄試件裂紋擴展過程，分析破壞形態；

4)分析處理試驗系統所得數據、曲線和試驗過程照片，得出結論。

2.3 試件破壞形態

試樣隨交變次數裂紋擴展圖如圖3所示。由圖3可知，在交變應力作用下，試樣疲勞破壞起始于預制裂紋的尖端缺口處，在循環次數較少時呈現出近似彈性的變形模式，但存在著塑性損傷累積效應；隨著循環次數的增多，缺口處表現出明顯的塑性變形，裂紋有一定的擴展；隨著循環次數的繼續增加，疲勞裂紋逐漸擴展，各試樣之間表現出不同擴展路徑，如圖4所示，疲勞裂紋基本與最大主應力方向呈90°，斷口表面存在明顯的微坑和韌窩，符合I型裂紋的破壞特征。

圖3 試樣(4#)隨交變次數裂紋擴展Fig.3 Crack growth of sample (No.4) with alternating times

圖4 試樣破壞形態Fig.4 Failure patterns of samples

3 結果與討論

3.1 疲勞裂紋擴展分析

為獲得da/dN數據，采用遞增多項式對(ai,Ni)進行擬合，采用遞增多項式擬合的4種載荷下的a-N曲線，如圖5所示。

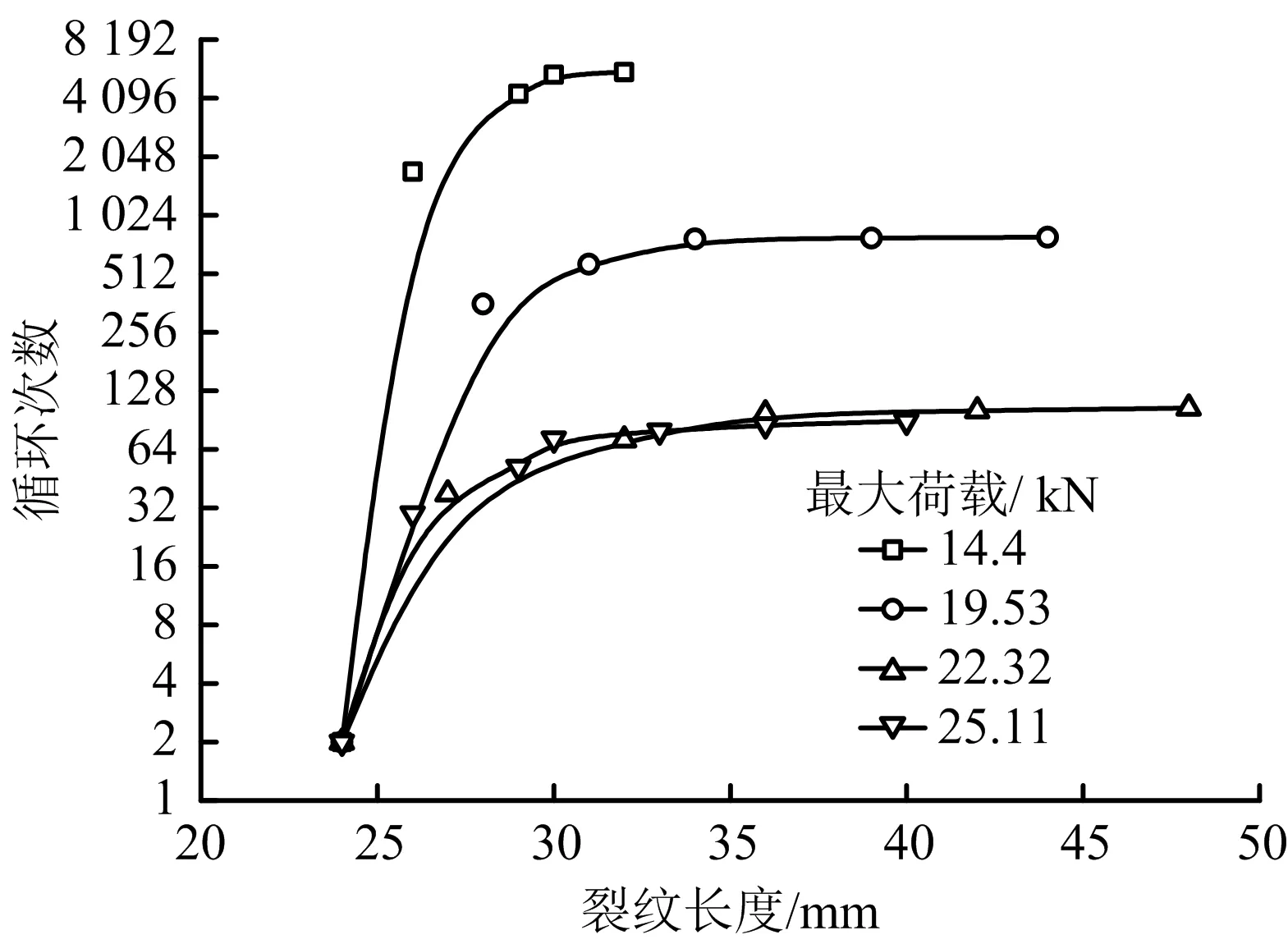
圖5 裂紋長度a與循環次數N關系圖Fig.5 Relationship between crack length a and cycle number N

通過計算不同應力下da/dN和應力強度因子ΔK，并對其取常用對數后，得到不同應力下lg(da/dN)-lg(ΔK)關系曲線，經過回歸處理，結果表現為1條直線，其中,lg(C)為直線的截距；m為直線的斜率。通過分析直線的方程，就可確定da/dN與ΔK的關系[13-14]。如圖6所示。

對圖6各數據進行回歸擬合即可得到Paris公式中的2個參數C和m，即可得到不同應力水平下疲勞裂紋擴展速率與應力強度因子之間的關系表達式，如下：

F=14.4 kN時：

da/dN=1.93×10-11(ΔK)2.754

(9)

F=19.53 kN時：

da/dN=2.53×10-10(ΔK)2.28

(10)

F=22.32 kN時：

da/dN=1.43×10-9(ΔK)2.21

(11)

F=25.11 kN時：

da/dN=1.18×10-9(ΔK)2.29

(12)

從各組試驗結果發現，在低應力水平或低應力強度因子ΔK下，試樣疲勞擴展速率較為緩慢，隨著應力水平的增加，da/dN越來越大，當應力水平達到某一臨界值時，裂紋擴展速率急劇增加，其低周疲勞壽命急劇下降。產生上述原因為：當裂紋擴展驅動力大于試樣的裂紋擴展阻力時，預制裂紋尖端會張開和產生塑性區，當裂紋擴展驅動力增大到一定時，已大于材料的破壞強度，裂紋尖端張開位移急劇增大，導致裂紋尖端的塑性區急劇擴大，此時極易發生斷裂。

3.2 疲勞裂紋擴展壽命計算

通過實驗可得同一應力比不同應力強度因子下裂紋擴展速率Paris公式中的C和m值。選取《城鎮設計燃氣規范》(GB50028—2006)[15]中規定的常用燃氣管道壁厚t=4 mm，外徑d=150 mm作為計算分析對象,對于低壓輸送鋼管，規定內壓變化為0～1.5 MPa。計算分析時，假定初始裂紋長3.5 mm，深度為1 mm，裂紋長寬比a/b為1.75。

至此，只需改變現場工程實踐管道輸送燃氣內壓Δp和裂紋深度a0，利用理論的公式，可得管道上初始裂紋擴展至臨界失穩尺寸的疲勞壽命。利用已得裂紋擴展規律，達到預測現場管道疲勞壽命的目的。

3.2.1 深度變化對疲勞壽命的影響規律

4種裂紋擴展速率的條件下，疲勞壽命N與裂紋深度的關系如圖7所示，管道的疲勞壽命與裂紋深度的變化近似成線性關系。由圖7可知，斜率的變化程度反映了應力強度因子對管道疲勞壽命下降的影響程度。在低應力水平或低ΔK下，管道疲勞壽命隨裂紋深度的增加下降較為緩慢，能夠較為明顯地觀測到壽命的變化。但是，隨著應力水平的增加，裂紋擴展速率不斷增大，管道的疲勞壽命急劇下降。

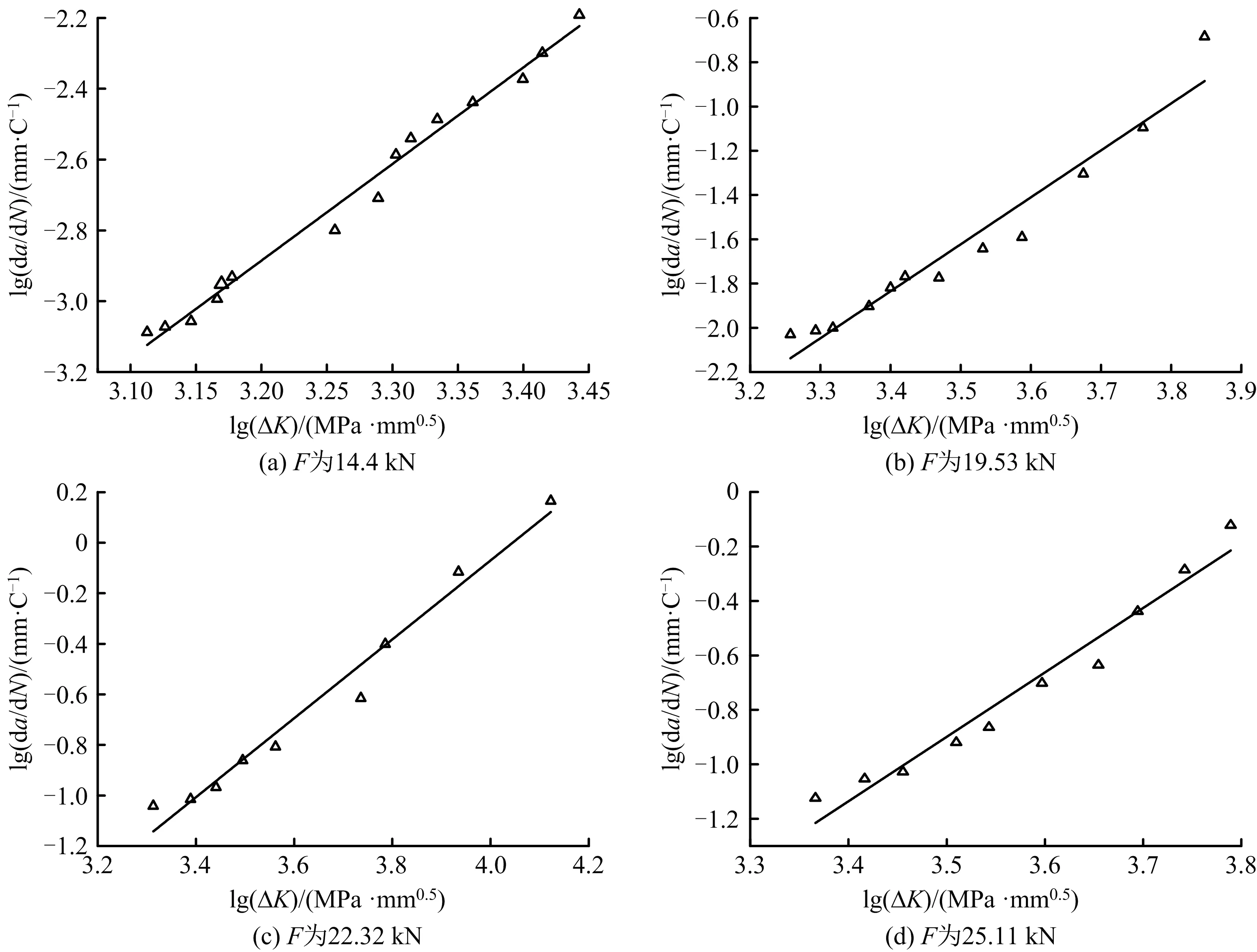
圖6 裂紋擴展速率隨應力強度因子的變化規律Fig.6 Variation laws of crack growth rate with stress intensity factor

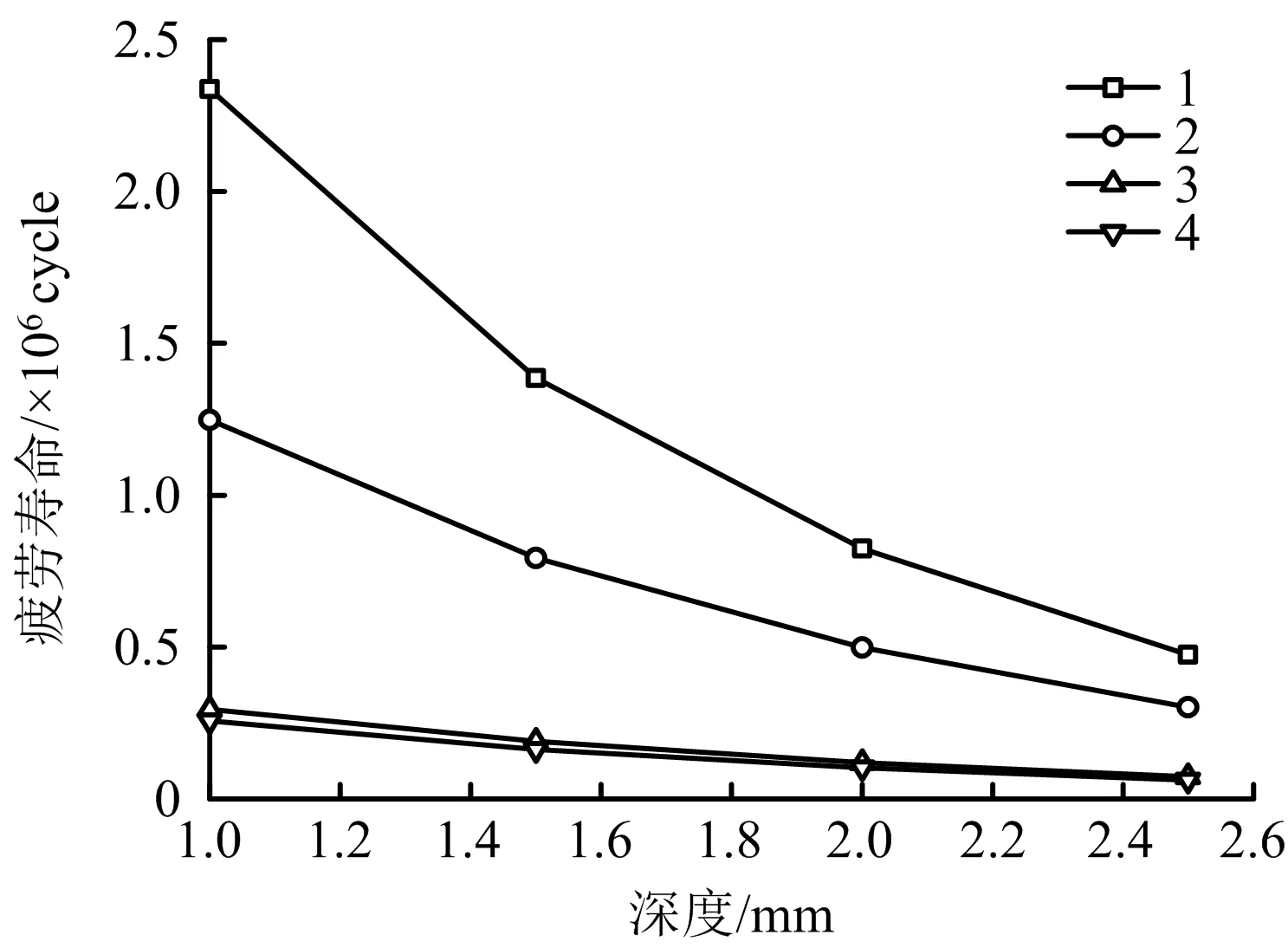
圖7 疲勞壽命N隨深度變化的影響規律Fig.7 Influence laws of fatigue life N with depth

在假定燃氣管道內壓幅值為1.5 MPa的條件下，在第1種和第2種擴展速率下，裂紋在深度上由1 mm擴展到2 mm，此時管道仍有較長的服務年限。而在第3種和第4種擴展速率條件下，當深度為2 mm時，疲勞壽命僅為102 370次，需要及時采取維護措施。

3.2.2 內壓幅值對疲勞壽命的影響規律

4種裂紋擴展速率的條件下，疲勞壽命N與內壓幅值的關系如圖8所示，曲線近似為指數為負的冪函數。由圖8可知，內壓幅值變化對含初始裂紋的燃氣管壽命更為敏感。疲勞壽命變化大致可以分為2個階段，第Ⅰ階段為安全階段，第Ⅱ階段為破壞階段。考慮計算管道壽命時，有必要考慮一定安全系數，取安全系數為1.5，在第Ⅰ階段內，4種裂紋擴展速率條件下管道至少工作壽命為31 a，滿足30 a的設計服務年限。為此，應控制內壓幅值，避免進入第Ⅱ階段。

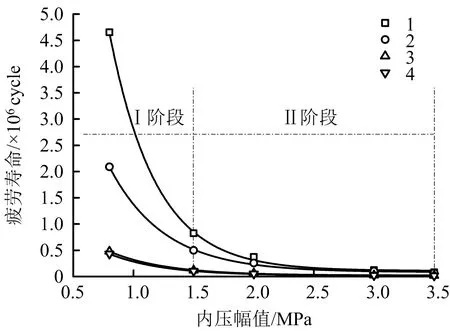
圖8 疲勞壽命N隨內壓變化的影響規律Fig.8 Influence laws of fatigue life N with change of internal pressure

在假定燃氣管道初始裂紋深度為2 mm的條件下，在第1種和第2種擴展速率條件下，當內壓幅值達到3 MPa時，就要及時進行維護。而在第3種和第4種擴展速率條件下，內壓幅值達到1.5 MPa，就需要及時補救。

通過對圖7～8的分析和比較，可得到以下結論：

對于含缺陷的低壓輸送管，疲勞壽命對于內壓幅值的變化Δp更為敏感，這就要求在日常生活中，輸送燃氣一定要保證內壓變化保持穩定，尤其對于含初始缺陷的燃氣管，內壓幅值應當盡量保持在1.5 MPa以下。

4 結論

1)對于含初始缺陷的低壓輸送燃氣管，內壓幅值的變化Δp影響疲勞壽命更為明顯，關系近似為指數為負的冪函數，內壓變化幅值應當盡量保持在1.5 MPa以下。

2)管道的疲勞壽命與裂紋深度的變化近似成線性關系。對于第1種和第2種擴展速率，隨著裂紋深度的變化，燃氣管道疲勞壽命下降程度較慢，可以及時采取措施。而對于第3種和第4種擴展速率，燃氣管疲勞壽命變化程度較大，當裂紋達到2 mm時，應及時采取維護等相應措施。