基于Monte Carlo法的腐蝕管道剩余壽命計算
馬樹鋒 王 勃 蘇海平 李署英 何蕓蕓
(1. 西安長慶科技工程有限責任公司,陜西 西安 710018;2. 蘇州市住房和城鄉建設局,江蘇 蘇州 215000)
0 引言
管道輸送以其運輸方便、輸送量大、密閉安全等優點,在油氣儲運過程中得到了廣泛的使用。埋地鋪設是管道鋪設最為常見的鋪設方式,而腐蝕則是造成埋地管道失效和破壞的主要原因。由于管道輸送的介質中常含有酸性腐蝕成分,管道所處的土壤環境復雜多變,這就使得管道的內外壁很容易受到腐蝕,造成穿孔、泄漏等危害,因此,如何進行油氣管道的可靠性評價已成為管道輸送的重要課題之一。以臨界壓力與工作壓力的干涉模型為基礎,應用Monte Carlo法計算腐蝕管道的失效概率和剩余壽命則是進行可靠性評價的有效途徑之一。
1 臨界壓力與工作壓力干涉模型
描述腐蝕缺陷的基本參量有缺陷的長度、寬度和深度,但由于腐蝕缺陷在周向的寬度對管道的承壓能力影響不大,一般不需要考慮[1]。目前,對于帶有軸向矩形腐蝕缺陷的管道,臨界應力的預測方程為[2]:

式中:
A為腐蝕缺陷在側面上的投影面積,mm2;
A0為腐蝕缺陷處管道的原始截面積,mm2;
M為Folias膨脹因子。
根據ASME B31G標準[3],管材的流變應力和Folias膨脹因子M分別為:

其中:
D為管道直徑,mm;
t為管道壁厚,mm。
假設管道在T0年檢測到的腐蝕長度和深度分別為d0和L0,則服役至T年時的腐蝕長度和深度為:

式中:
RL為徑向腐蝕速度,mm/a;
Rd為軸向腐蝕速度,mm/a。
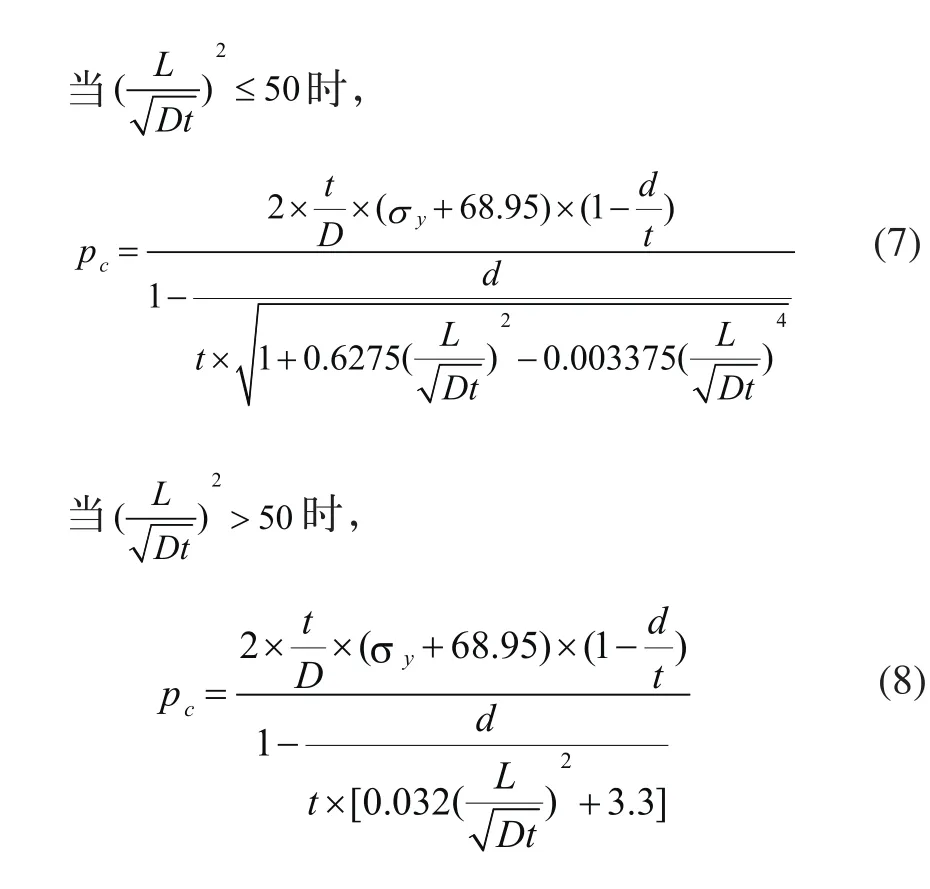
由于臨界壓力pc與工作壓力p相對獨立,即可根據可靠性理論建立臨界壓力與工作壓力的干涉模型,Z為干涉隨機變量[4]:

當Z>0時,管道處于可靠狀態;當Z=0時,管道處于極限狀態;當Z<0時,管道處于失效狀態。
2 Monte Carlo法的應用
Monte Carlo法是一種隨機模擬方法,又稱隨機抽樣技術或統計技術方法,以數理統計為基礎,既能求解確定性問題,也能求解隨機性問題[5]。應用Monte Carlo時,不必知道腐蝕速率的具體值,只需知道其的概率分布即可求出腐蝕管道的失效概率。由于Monte Carlo法是以數量較多的樣本為基礎的概率統計,因此,如何產生隨機數則成為Monte Carlo法的重中之重。
對于隨機數的產生,常用的工具是MATLAB軟件。它提供了常用隨機變量分布類型的隨機數發生器[6]。例如normrnd(μ,σ,m,n),它是用于產生服從正態分布N(μ,σ2)的m行n列的隨機數組。
3 應用實例
以某鋼制輸氣管道為例,其基本參數如下:管道規格為Φ355×7mm,管材最小屈服強度為394MPa,工作運行壓力為3.9MPa,已工作15年,對其中連續5年的腐蝕數據進行統計得到:平均腐蝕深度為1.8mm;腐蝕長度為260mm。忽略其它微小因素(如管徑、工作壓力),主要考慮缺陷的軸向腐蝕速率和徑向腐蝕速率的分布,采用數理統計的方法得出其軸向腐蝕速率服從正態分布N(17.6,2.82),徑向腐蝕速率服從正態分布N(0.107,0.0312)。
在MATLAB中編寫相應的程序計算管道失效概率,順序流程圖如圖1所示。應用Monte Carlo法時,由于只要樣本的數量足夠多,其計算結果就越接近于真實值,因此所得到的結果應該是一條連續的曲線。

圖1 MATLAB流程圖
本文取106個樣本次進行模擬,得到的失效概率和可靠度與服役年限數據如表1所示,失效概率和可靠度與服役年限曲線圖如圖2所示。
從表1和圖2中可以看出,在前15年中,管道的失效概率為0,管道幾乎不會發生腐蝕破壞,但隨著服役年限的增加,其失效概率迅速增加,可靠度迅速降低,管道面臨的腐蝕破壞風險大大增加。對于處在一類地區的管道,對應低風險情況,可接受失效概率F0取10-2,目標可靠度R0取0.99;對于處在二類和三類地區的管道,對應中等風險,F0取10-3,R0取0.999;對于處在四類地區的管道,對應高風險,F0取10-5,R0取0.99999[7]。由于該管道處于二類地區,F0=10-2,R0=0.999,因此被檢查區域內管道剩余壽命為19年。19年后若想繼續使用該管道,需進行相應的修復和防腐工作,以延長其剩余壽命。

表1 失效概率和可靠度與服役年限數據

圖2 失效概率和可靠度與服役年限曲線圖
4 結論
應用Monte Carlo法可以快速有效的計算出腐蝕管道的失效概率和剩余壽命,它具有簡單易懂、快速高效等優點,在可靠性分析當中的應用是完全可行的。管道的防腐工作以剩余壽命為分界線,分界線前后,腐蝕防護工作的重點和工作量不同。

