基于第一性原理的層狀ZnO結構和化學鍵研究

蘇亞拉

摘 要：第一性原理系統的研究了層狀ZnO的結構和化學鍵的特性。計算的結果表明層狀ZnO既存在共價鍵又有離子鍵特性與其他人的結論相一致。

關鍵詞：層狀ZnO;幾何結構;化學鍵

中圖分類號：TB 文獻標識碼：A doi：10.19311/j.cnki.1672-3198.2019.34.089

0 引言

早在2010年，Pueyo等人就利用Zn4O4為前驅體成功地合成了層狀六角結構的ZnO相。室溫下，它的帶隙能為～3.5eV，比纖鋅礦ZnO略大。通過結構分析表明，這種層狀ZnO的a-b面上Zn-O鍵長1.79，小于纖鋅礦（B4）ZnO中Zn-O鍵長1.94。這種層狀ZnO表現出與纖鋅礦ZnO相近的光學帶隙，有可能成為一種新型的光電子材料。Rakshit和Mahadevan首次通過第一性原理計算討論了這種層狀ZnO的穩定性。Molepo and Joubert預測這種層狀ZnO可以通過纖鋅礦ZnO高壓相變獲得，相變壓力24.6GPa，但尚需進一步的實驗驗證。2015年，Wang等人利用超軟贗勢計算了這種層狀ZnO的電子結構和光學性質。然而，對于層狀ZnO物理特性的研究仍然沒有深入的探討，尤其是它的化學鍵。本文基于第一性原理密度泛函理論研究層狀ZnO的化學鍵屬性。

1 計算方法

基于密度泛函理論，計算采用模守恒贗勢交換關聯相互作用采用廣義梯度近似（GGA）泛函。Zn和O的電子構型分別為3d104s2和2s22p4。能量優化采用 BFGS算法，平面波的截斷能為900eV。B4相和層狀Bk相ZnO的全布里淵區k點求和為7×7×4。測試結果表明進一步增加平面波的截斷能和k點數目幾乎對計算結果沒有影響。

2 結果與討論

2.1 結構與參數

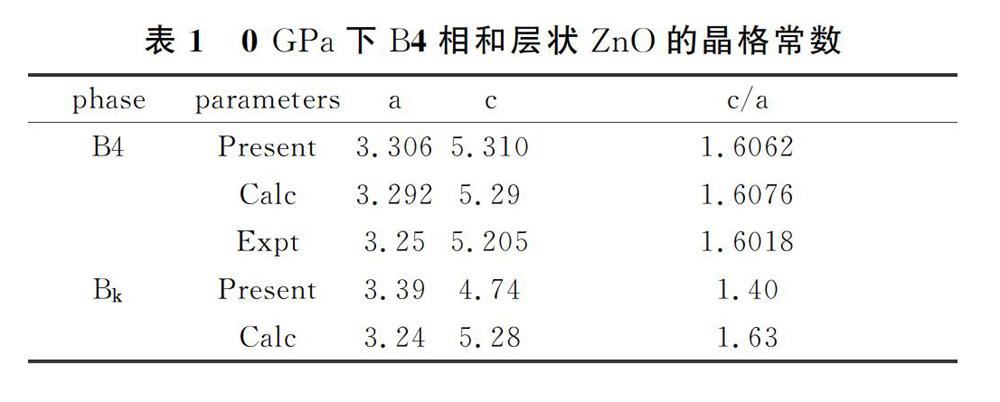
為了評價計算結果的可靠性，我們首先幾何優化了0GPa下B4相和層狀ZnO的晶格常數（a，c，c/a）并與實驗結果和他人的理論結果進行了比較，如表1所示。從表中可以看出，B4相和層狀ZnO的計算結果與實驗結果和他人的計算結果基本一致，基本參數a、c、c/a的計算誤差小于2%，說明我們采用的計算方法和參數設置是可靠的。

2.2 分析化學鍵

表1列出了0 GPa下B4相以及0 GPa和11.3GPa下層狀ZnO化學鍵鍵長及其對應的密力肯布居數。0 GPa下B4相計算的鍵長與前人的結果基本相同。從表中可以看出，0 GPa下B4相的鍵長比0 GPa下層狀ZnO化學鍵要長對應的密力肯布居數基本上沒有變化。然而，在相轉變壓強下，層狀ZnO化學鍵的鍵長減小。為了判斷是否是離子鍵還是共價鍵，這可通過化學鍵理論分析。張等人提出過晶體的化學鍵理論，它是以化學鍵鍵能為基礎的半經驗方法。計算背景為：首先通過結構分析，將復雜的分子化學式分解成簡單的二元分子式的組合，然后可以計算離子鍵和共價鍵的代表參數。對于ZnO本身就是最簡單的二元分子式，如表2所示，其中代表鍵長。從表中數據可以看出，0 GPa下B4相計算得到化學鍵的異極化能大于同極化，這表明它是以離子性為主，與Phillips結論一致。但是我們計算的離子性標定為0.803大于Phillips的離子性標定0.616，這歸因于計算的平均磁化率不同有關。對于0 GPa下層狀ZnO，同樣是以離子性為主。相轉變后離子性標定減小，說明隨著壓強的增大離子性降低，這與我們以前的結論相同。通過計算得到不同化學鍵的離子性結果也能證明這一結論。總之，層狀ZnO與B4相的ZnO一樣，即表現出離子鍵又表現共價鍵特性。

3 結果

利用密度泛函理論研究了層狀ZnO的幾何結構參數和化學鍵的特性。根據化學鍵理論計算結果表明層狀ZnO既存在共價鍵又有離子鍵特性。

參考文獻

[1]Pueyo C L，Siroky S，Landsmann S，et al.Molecular precursor route to a metastable form of zinc oxide[J].Chem.Mater，2010，（22）：4263.

[2]Rakshit B and Mahadevan P.Stability of the bulk phase of layered ZnO[J].Phys.Rev.Lett，2011，（107）：085508.

[3]Molepo M P and Joubert D P.Computational study of the structural phases of ZnO[J].Phys .Rev.B，2011，（84）：094110.

[4]Wang Q B，Zhou C，Wu J，et al.GGA+U study of the electronic and optical properties of hexagonal BN phase ZnO under pressure[J].Comp.Mater.Sci，2015，（102）：196.

[5]Hamann D R，Schluter M，and Chiang C.Norm conserving pseudopotentials[J].J.Phys.Rev.Lett，1979，（43）：1494.

[6]Perdew J P，Burke K，and Ernzerhof M.Generalized gradient approximation made simple[J].Phys.Rev.Lett，1996，（77）：3865.

[7]Jaffe J E，Snyder J A，and Lin Z.LDA and GGA calculations for high-pressure phase transitions in ZnO and MgO[J].Phys.Rev.B，2000，（62）：1660.

[8]Desgreniers S.Structural and compressive parameters high density phases of ZnO[J].Phys.Rev.B，1998，（58）：14102-14105.

[9]Sun J and Wang H T.Ab initio investigations of optical properties of the high-pressure phases of ZnO[J].Phys Rev B，2005，（71）：125132.

[10]Fan C，Wang Q，Li L X，et al. Bulk moduli of wurtzite，zinc-blende，and rocksalt phases of ZnO from chemical bond method and density functional theory[J].Appl.Phys.Lett，2008，（92）：101917.

[11]Zhang S，Li H，Li L，et al. Calculation of bulk modulus on carbon nitrides with chemical bond method[J].Appl Phys Lett，2007，（91）：251905.

[12]Phillips J C.Bonds and Bands in semiconductors Academic[Z].New York，1973.

[13]Vechten J A V.Quantum Dielectric Theory of Electronegativity in Covalent Systems.Electronic Dielectric Constant[J].Phys Rev，1969，（182）：891.

[14]Serrano J，Romero A H，Manjon F J，et al. Pressure dependence of the lattice dynamics of ZnO：An ab initio approach[J].Phys.Rev.B，2004，（69）：094306.