基于近場聲全息的目標反射聲場重建方法研究

陳新寧

(1.91388 部隊，廣東 湛江 524022;2.水聲對抗技術重點實驗室，廣東 湛江 524022)

0 引 言

使用聲納設備可以對潛艇、水面艦艇、水雷、魚雷等水下目標進行探測[1-2]。為了提高航行器的聲隱身性能，需要對潛艇等航行器殼體表面的聲波反射情況進行分析[3-5]，從而進行外形改造或特殊處理來降低反射聲波強度。

對目標反射強度的測量一直是采用水聽器直接進行的，但是目標與水聽器距離過小時，水聽器本身會成為一個反射體，影響聲場的測量精度。禹建[6]運用Matlab軟件對潛艇、魚雷和水雷這3種常見水下目標的回聲信號進行了模擬與仿真，對獲得的不同水下目標的回聲信號的相關特性進行了研究；楊鵬等[7]根據Kirchohoff近似公式建立了一種水下目標回波亮點特性計算的新方法，將回波亮點特性中的面元計算轉化為對圖形像素點相關信息的計算，對不同傳播距離的面元反射特性求和得到水下復雜目標回波亮點特征；譚昕等[8]分析了不同外形水雷的目標強度與隱身之間的關系，并對一些典型外形進行了目標強度計算。以上論述雖然都可得到水下目標的反射聲波特性，卻無法得到水下目標表面的反射聲常情況。近場聲全息技術[9]（NAH）是上世紀80年代由傳統聲全息技術演變而來的一種非常有效的聲場推算及聲場可視化技術，為獲得航行器殼體表面反射聲場提供了技術手段。1980年，Williams等[10]正式提出了基于空間Fourier變換的近場聲全息理論。國內對近場聲全息的研究，大多是以基于空間Fourier變換的方法為主；崔志光等[11]利用近場聲全息技術進行聲吶目標強度測量，但只測量幾個點進行亮點重建，誤差較大；豐少偉等[12]利用近場聲全息技術研究了實艇測試中存在的海底聲反射問題，得到海底吸聲量與測試精度的關系，驗證了近場聲全息技術在應對聲場反射問題的有效性。

本文在空間聲場變換算法(STSF)的基礎上，以一個膠囊狀仿潛艇模型為實驗對象，對其表面反射聲場進行反向重構仿真分析，并在 5 m×3 m×3.5 m的消聲水池內進行實驗驗證，最后根據誤差分析結果驗證近場聲全息技術重構水下航行器表面反射聲場的可行性和有效性。

1 基本理論

均勻理想流體介質中的小振幅聲波的波動方程為

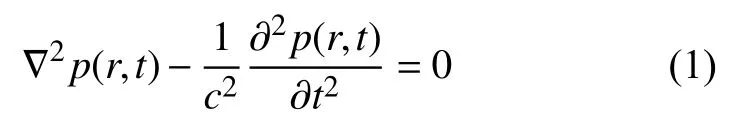
式中：?2——Laplace算子；

p(r,t)——聲場中任意一點處r的聲壓；

c——聲波傳播的速度。

對波動方程進行Fourier變換，得到不依賴于時間變量的Helmholtz方程：

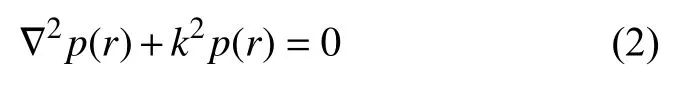
其中，k=ω/c，為波數； ω =2πf，為角頻率。

定義全息面(測量面)用H表示，重構面(源面)用S表示。

在Dirichlet邊界條件下，對于zH＞zS的空間為自由場的情況，式(2)的解為

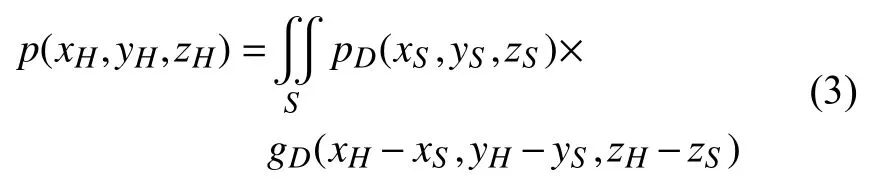
gD為Dirichlet邊界條件下無窮大平面的Green函數：

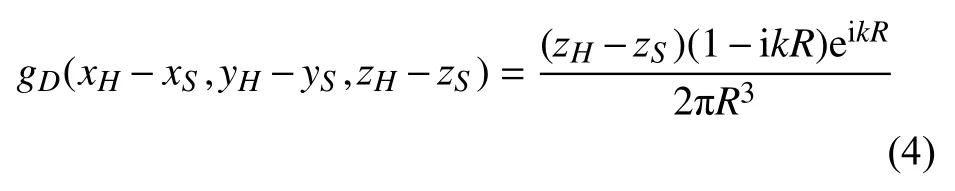
式中：

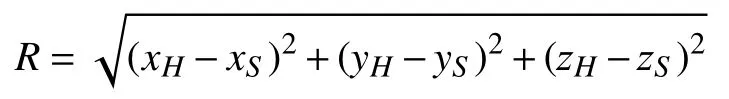
對式(4)兩邊取空間Fourier變換，將空域卷積化為波數域中角譜的乘積：

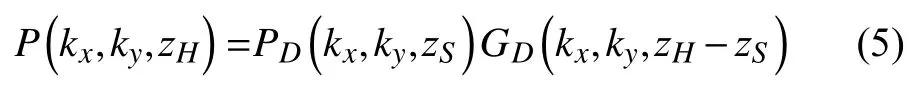
其中，P(kx,ky,zH)為聲壓p(xH,yH,zH)的空間Fourier變換；PD(kx,ky,zS為邊)界條件pD(xS,yS,zS)的Fourier變換；GDkx,ky,zH-zS為Green函數的空間Fourier變換，解析表達式為

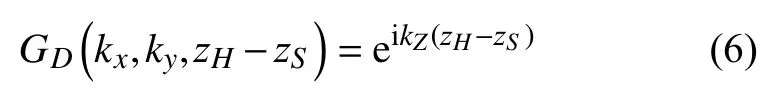
同樣可得反向重構公式：

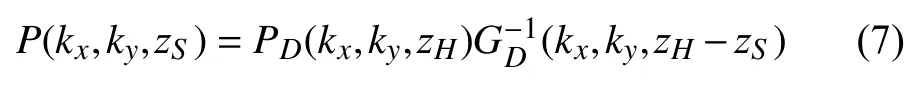
由式（7）可得重構面聲壓：

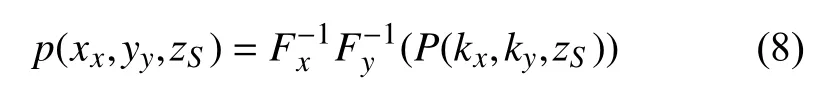
聲場重建公式（7）的推導過程中沒有近似，故其結論是嚴格的,本身不存在誤差。但在實際計算中，由于測量孔徑有限，會引起卷繞誤差[13]；由于全息數據邊緣的不連續會引起邊緣誤差；同時測量環境中的噪聲以及測量儀器本身的誤差都會造成全息面質點振速測量結果的不準確。這些數據中所包含的誤差成分會被 e-kz(zH-zS)按指數所放大，尤其是對于高波數區域，即當波數分量很大時，測量值的誤差對結果的影響非常嚴重，甚至會造成重建結果失真。

以重建誤差[14]作為指標，來評價重建效果，本文所用重建誤差的計算公式與文獻[14]一致，計算公式為

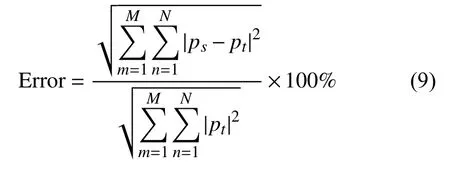
式中：pt——重建面理論聲壓值；

ps——重建面計算聲壓值。

本節推算了二維平面聲壓的構建方法和近場聲全息基本理論，作為本文聲場推算方法的計算依據。

2 仿真驗證

仿真測量示意圖如圖1所示，在直角坐標系中，膠囊狀仿潛艇模型的中心位于坐標原點，模型為空心殼體，模型長度L=19 cm，半徑r=3 cm。發射換能器發射頻率為30 kHz的正弦脈沖信號，聲波經膠囊狀仿潛艇模型反射后，使用多物理場仿真軟件comsol分別仿真計算重構面及測量面的反射聲場分布。仿真計算時，將有限大小的測量面離散成500×500個采樣點，x和y方向的采樣點間距都設為0.2 cm，重構面與測量面平行，面積大小與測量面相等。水中聲速設為 1 480 m/s，密度為 1 000 kg/m3，測量面距離模型中心為20 cm，重構面距離模型中心 15 cm。

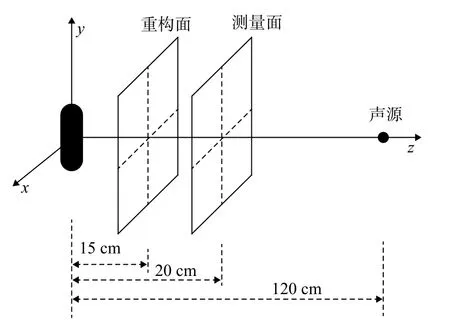
圖1 反射聲場測量仿真模型

為了更直觀地觀察聲場起伏狀態，只給出聲壓分布沿x軸和y軸的剖面圖進行分析。仿真計算出的重構面聲壓分布，作為真實值與推算值進行對比，如圖2所示，圖2（a）為重構面上的x方向上的聲壓分布，圖2（b）為重構面上的y方向上的聲壓分布。

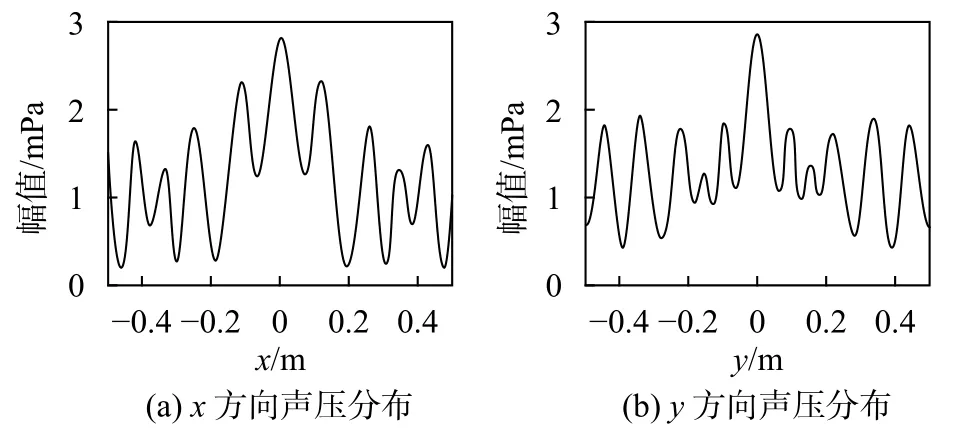
圖2 重構面理論聲壓分布仿真計算結果

由圖可知，由膠囊狀反射體表面反射的聲場是不規則的，引起反射的部位不僅僅是柱體圓柱表面，兩端的反射也是存在的，并且是不規則的，同時膠囊反射體中間的反射強度最大。所以當利用水聽器貼近反射體表面進行發射聲場測量時，水聽器本身也會引起反射，造成被測聲場的混亂，形成較大的測量誤差。

同時，仿真計算出測量面的聲壓分布后，利用NAH技術，依據式（7）由測量面聲壓分布反向推算出重構面聲壓分布，推算結果如圖3所示，圖3（a）為重構面上的x方向上的聲壓分布，圖3（b）為重構面上的y方向上的聲壓分布。

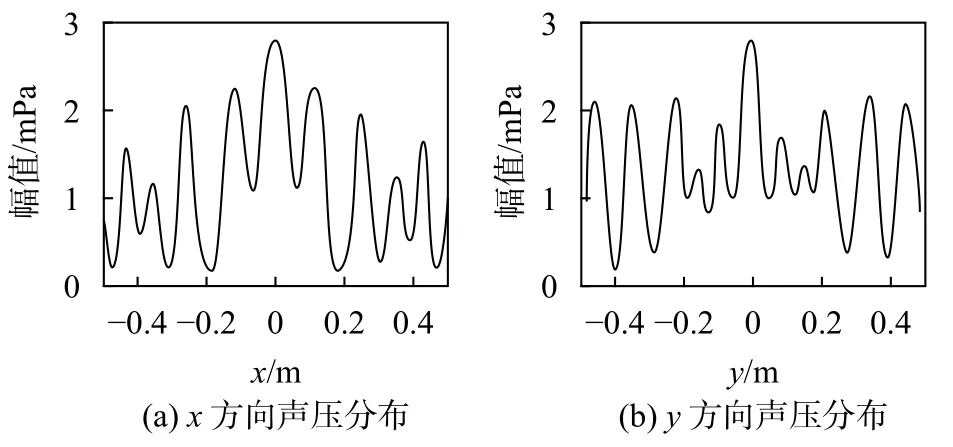
圖3 重構面推算聲壓分布結果

由重構面仿真結果及推算結果進行對比可知，利用近場聲全息技術推算出的反射體表面的反射聲場曲線與理論反射聲場曲線基本一致，對推算結果進行定量分析，根據式（9）可得誤差為8.64%。因此，基于空間傅里葉變換的近場聲全息技術的聲場推算方法可以有效得到重構面上的聲壓分布。因此，將近場聲全息技術應用于識別水下目標殼體表面的反射聲場信息，為水下航行器殼體的外形設計或材料選取提供了一種檢測的新思路。

3 近場聲全息實驗研究

實驗在一個 5 m×3 m×3.5 m 的消聲水池中進行，利用填充脈沖信號作為發射信號源，以便在空間上隔開直達信號、反射信號以及樣品邊緣衍射的特性，以降低測量低頻限，獲得可靠的測量結果。

測量系統如圖4所示，主要包括信號源、功率放大器、高精度三維控制機構、球形水聽器、前置放大器、數字示波器、計算機等。小球換能器、水聽器、膠囊狀殼體按照仿真位置放置，此時直達波與反射波聲程差最小為30 cm，因此信號源發射頻率為30 kHz時，波長為5 cm，為了隔開直達信號與反射信號，脈沖循環數應小于6個。實驗中信號源發射頻率為30 kHz，脈沖數為4個的填充脈沖信號，經過功率放大器放大后激勵小球換能器發射聲波。水聽器安裝在控制機構上，控制機構最小步進距離為0.02 mm，球形水聽器接收的信號經過前置放大器后，再由數字示波器進行采集和顯示。為了獲得不同測量點復聲壓，通過計算機控制步進機構、使水聽器完成對一點聲場掃描后，運動至下一掃描點，直至完成所有測量點的掃描；通過對數字示波器在每個測量點采集的信號進行讀取，得到測量平面的聲壓值。

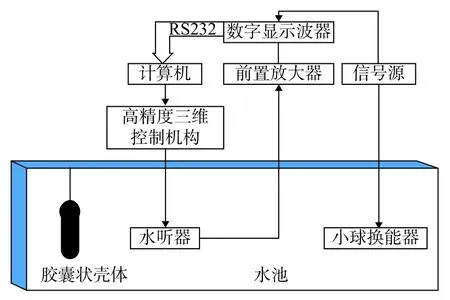
圖4 聲場測量系統示意圖

實驗選用膠囊狀仿潛艇模型，并按仿真所設定的參數進行測量與聲場重構。測量面x和y方向的采樣點間距都為0.5 cm，沿著測量面內x和y軸測得的點數分別為200和200，重構面與測量面平行，面積大小與測量面相等。

為了驗證重構算法的正確性，使用水聽器直接測量重構面的聲場分布，圖5所示的是重構面x方向軸線聲壓和y方向軸線實測聲壓分布。

同時，在得到測量面上的聲壓分布后，依據公式（7）推算得到重構面聲場信息，如圖6所示為推算得到的重構面x方向軸線聲壓和y方向軸線聲壓。

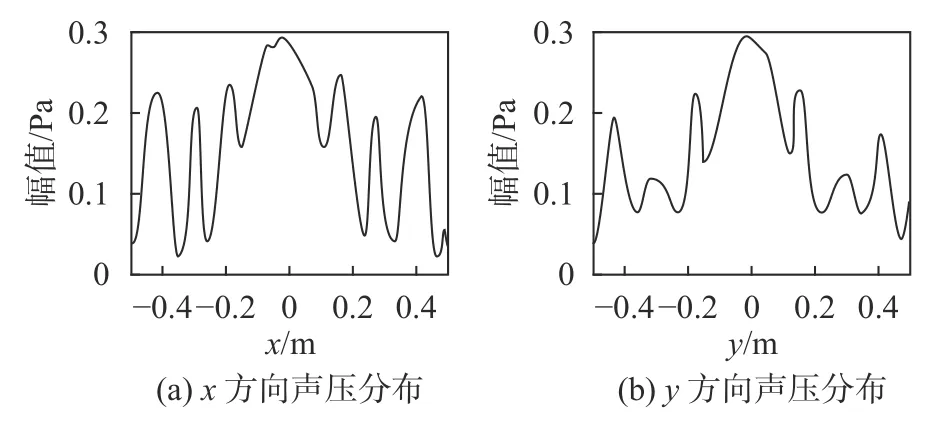
圖5 重構面實測聲壓分布

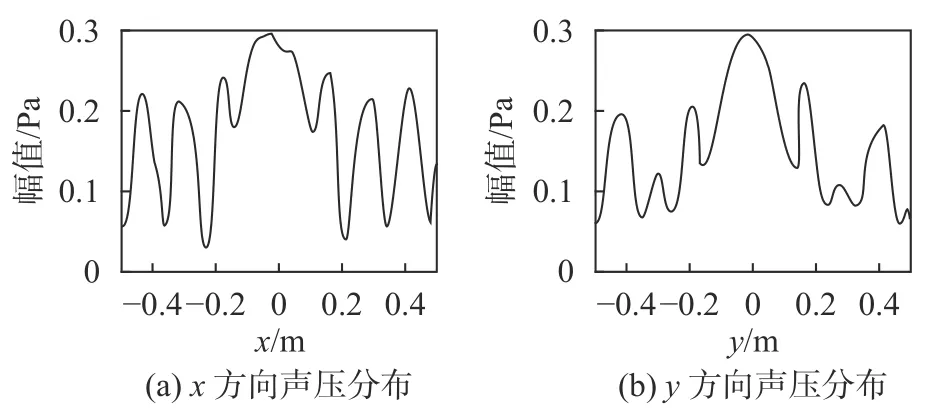
圖6 重構面推算聲壓分布

通過圖5和圖6比較可知，推算結果與實驗結果趨勢大致一樣，根據式（9）可得實驗誤差為9.48%，與仿真結果基本一致。分析其誤差來源，主要有4點：

1）懸掛的膠囊狀殼體傾斜，從而引起推算誤差。

2）在近場數據采集過程中，由于環境噪聲和電干擾的影響等引起的測量誤差會影響結果的準確性。

3）由于測量的點數是有限的，測量面不可能包含所有的聲場信息，會引起信息的泄露，造成有限孔徑誤差。

4）快速傅里葉變換雖然加快了數據計算速度，但也帶入了卷繞誤差。

4 結束語

本文通過對膠囊狀殼體表面的的輻射聲場進行測量。以空間傅里葉變換的近場聲全息技術作為理論基礎，提供了一種測得潛艇等水下航行器表面反射聲場信息的新思路。通過對仿潛艇模型殼體的聲場的推算結果，從理論推算和實驗測量兩個方面驗證了推算方法，證明該測量方法可應用于檢測水下航行器表面聲波的反射情況，對分析潛艇等水下航行器的聲隱身性能提供了一種技術手段。