浮置板下聲子晶體隔振器帶隙特性研究

農興中，李 祥，劉堂輝，盛 曦，王 平，趙才友

（1.廣州地鐵設計研究院股份有限公司， 廣東 廣州 510010；2.西南交通大學高速鐵路線路工程教育部重點實驗室，四川 成都 610031；3.西南交通大學土木工程學院，四川 成都 610031）

隨著我國地鐵的大規模修建，地鐵運行引起的環境振動越來越影響人們的生產與生活[1]，地鐵誘發的地面建筑振動頻率成分主要為80 Hz以下的低頻振動[2]，而人體對低頻振動較為敏感[3-4]，因此地鐵減振措施主要針對于低頻振動.浮置板道床作為地鐵常用減振措施，通過道床減振的方式隔離向環境土壤傳播的垂向振動.浮置板軌道系統實現隔振的原理是在軌道與基礎之間插入一個固有頻率極低的質量-彈簧系統，由浮置板道床提供較大質量，由浮置板板下支承提供較低的垂向剛度，可衰減頻率范圍在倍固有頻率以上的振動成分[5].常用的浮置板板下支承類型有鋼彈簧與橡膠隔振器.

目前聲子晶體在減振降噪領域的研究成果豐富，1993年，Kushwaha[6]在研究鎳/鋁二維固體周期復合介質時首次提出了聲子晶體的概念；Koo等[7]將聲子晶體引入管路系統中，將管路加周期彈性支撐，得到了彎曲振動帶隙并進行實驗驗證，發現其帶隙對彎曲振動有一定隔振效果；Sheng等[8]提出了聲子晶體的局域共振帶隙機理，這標志著聲子晶體研究的重大突破；Yu等[9]率先將聲子晶體理論引入到梁板類結構設計中，實現了利用帶隙特性抑制一定頻率范圍內的振動傳播.本文作者所在課題組已將聲子晶體理論初步應用于軌道結構研究中，其中文獻[10]基于聲子晶體理論提出了一種用于浮置板下滿鋪支承的減振墊板，進行了一定的理論計算與帶隙優化工作，但是未考慮減振墊對整體軌道減振效果的影響，且制造精度和難度較高.因此，本文對文獻[10]中提出的元胞結構進行優化，將滿鋪的減振墊改為點支撐的隔振器，通過結構設計使其垂向剛度與傳統鋼彈簧一致，建立了三維聲子晶體隔振器浮置板軌道有限元模型，計算了整體結構的力傳遞率，并與傳統鋼彈簧浮置板軌道的計算結果進行對比.此外，計算了聲子晶體隔振器的垂向剛度.

1 聲子晶體隔振器簡介

聲子晶體是由兩種或兩種以上彈性介質組成的具有彈性波帶隙的周期復合材料.彈性波在聲子晶體中傳播時，受其內部周期結構的作用，形成特殊的色散關系，將沒有色散關系曲線的頻率范圍稱為帶隙.理論上，帶隙頻率范圍的彈性波傳播被抑制，而其它頻率范圍（稱為通帶）的彈性波將在色散關系的作用下無損耗地傳播.聲子晶體的帶隙機理有兩種，分別為布拉格散射機理與基于共振機理，本文的聲子晶體隔振器基于聲子晶體局域共振機理，與傳統鋼彈簧的安裝位置一致，聲子晶體橡膠隔振器浮置板軌道結構示意圖如圖1所示.

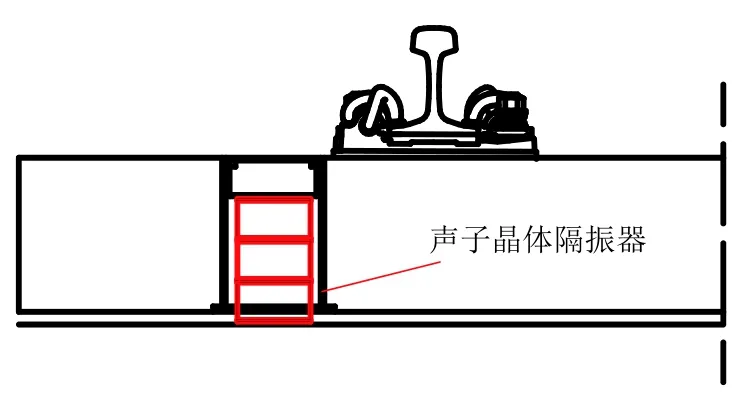
圖 1 聲子晶體隔振器浮置板軌道結構示意Fig.1 Schematic diagram of the floating slab track with vibration isolators of phononic crystals

本文所設計的聲子晶體隔振器一維聲子晶體結構元胞由橡膠墊層、鋼散射體、軟橡膠材料和基體外殼（鋁合金）組成，如圖2（a）所示，聲子晶體隔振器由3個元胞構成.軟橡膠和鋼散射體形成局域振子，提供局域共振型帶隙，而基體外殼和橡膠墊層主要提供垂向剛度.聲子晶體隔振器元胞幾何尺寸如圖2（b）所示，上圖為聲子晶體元胞俯視圖的一半，下圖為聲子晶體元胞的前視剖面圖，幾何材料參數如表1所示.

聲子晶體隔振器尺寸與鋼彈簧隔振器相差不大，可匹配現有浮置板鋼彈簧隔振器的空間設計，將其置于浮置板與基底之間.聲子晶體隔振器作為功能部件，可產生低頻寬帶的帶隙，抑制帶隙頻率范圍內的彈性波從浮置板道床向基底的傳播；作為結構部件，可為浮置板提供垂向剛度，形成固有頻率較低的質量-彈簧系統[11]，保留傳統浮置板道床的減振效果.

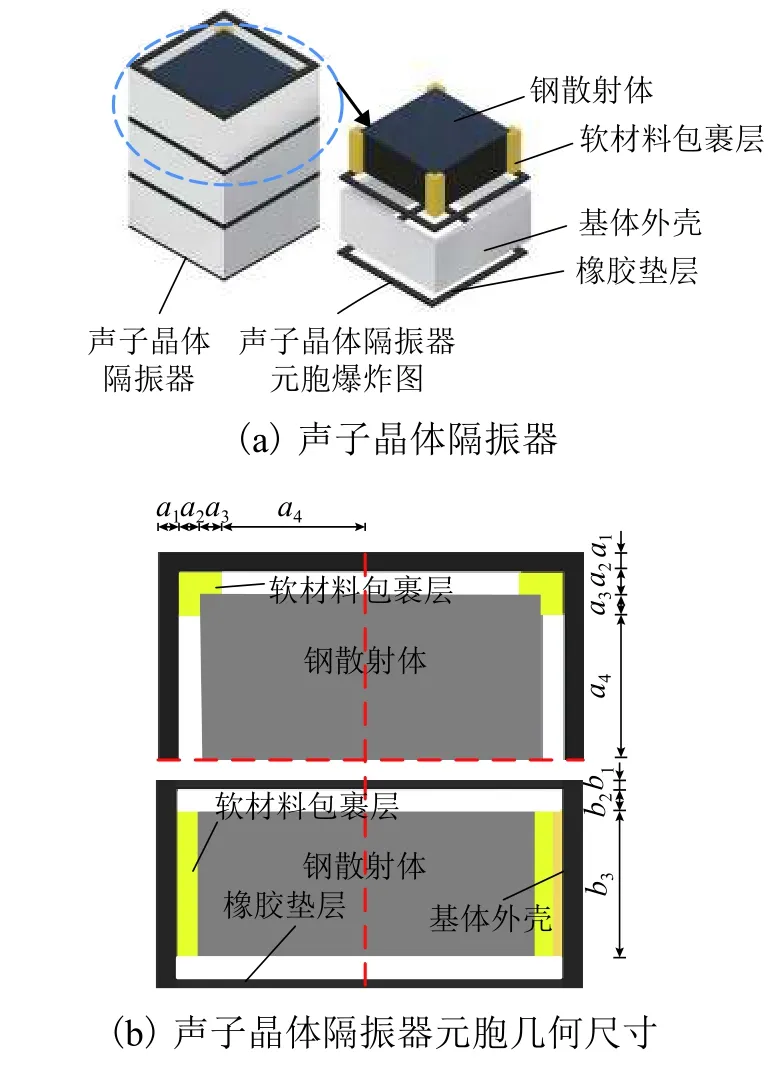
圖 2 聲子晶體隔振器結構Fig.2 Vibtration isolator structure of phononic crystals

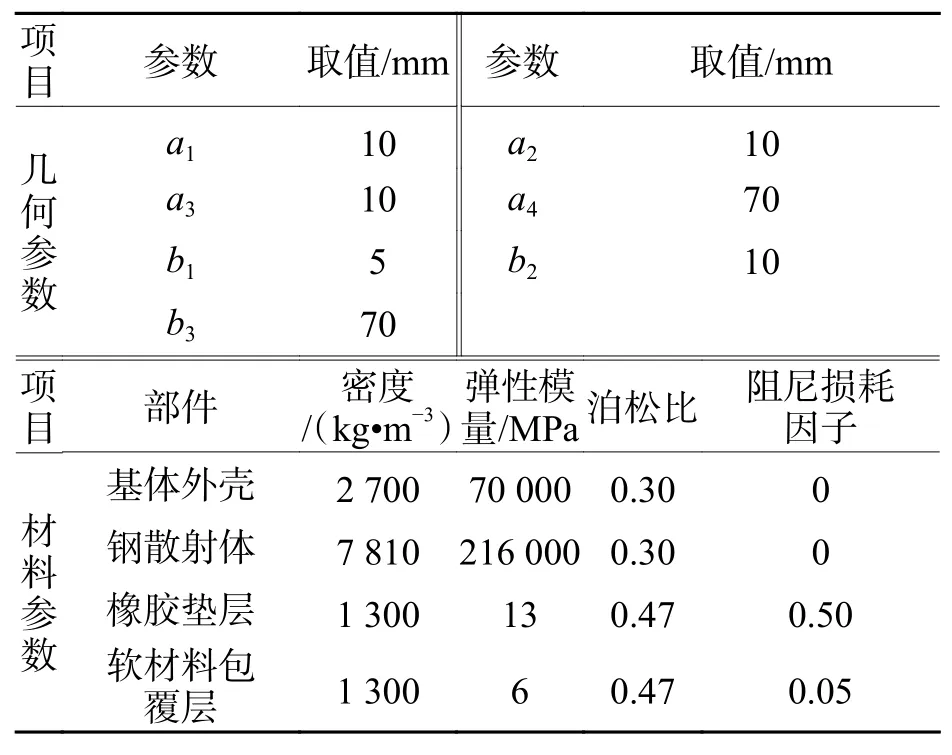
表 1 聲子晶體隔振器元胞部分參數Tab.1 Some parameters related to vibtration isolators and its phononic crystal cell

2 聲子晶體隔振器帶隙特性

2.1 能帶結構

當理想彈性介質（連續、均勻、各向同性及完全彈性）發生小變形時，其運動控制方程（不計體力）可表示為[12]

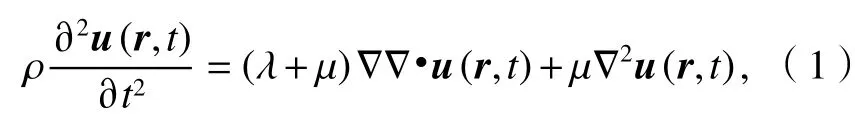
式中：u（r,t）為位移波函數；r為位置坐標；t為時間；ρ為密度；λ和μ為 Lamé常數； ? 為 Hamilton微分算子.

式（1）中的解滿足 Bloch定理[13]：

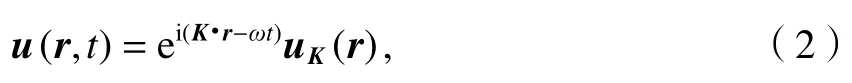
式中：K為倒空間內的波矢（一維聲子晶體為k）；uK（r）為波幅.由于結構的周期性，uK（r）可表示為周期函數[14]：

式中：R為正格矢.將式（3）代入到式（2）可得周期性邊界條件：

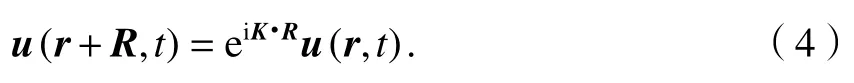
將位移波函數和周期性邊界條件代入控制方程，可得到包含波動頻率與波矢關系的特征值，即能帶結構[15].聲子晶體隔振器能帶結構可通過有限元軟件COMSOL Multiphysics計算求得，對圖2所示的元胞結構進行實體建模，在元胞上下截面設置周期性邊界條件，令波矢掃描一維聲子晶體不可越 Brillouin區邊界（0，π/b），b為元胞晶格常數，b= 2b1+ 2b2+b3，計算不同波矢下的特征頻率.為了減小網格尺寸對100 Hz以下計算結果的影響，最大單元網格尺寸不超過0.01 m.聲子晶體隔振器前10階能帶結構曲線計算結果如圖3所示.

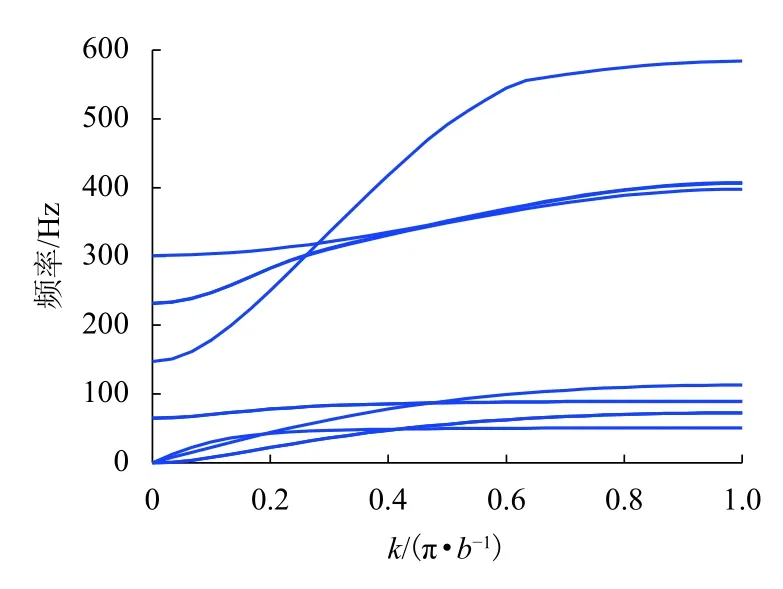
圖 3 聲子晶體隔振器能帶結構Fig.3 Band structure of vibration isolators of phononic crystals

對于圖3所示的能帶結構，盡管所有能帶曲線均表征傳播方向為軸向的導波，但并非所有導波的振動方向為軸向.當k= π/b時，聲子晶體隔振器前10階導波模態如圖4所示.

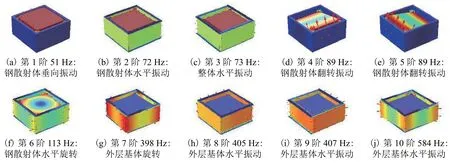
圖 4 聲子晶體隔振器前10階導波模態Fig.4 First 10th guided wave modal of isolators

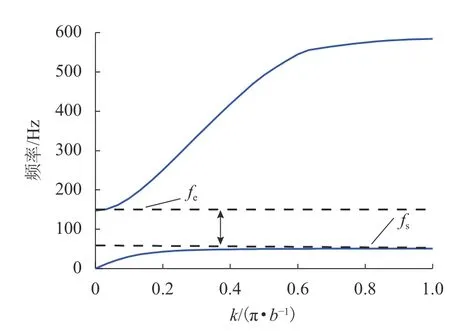
圖 5 振動方向為垂向的聲子晶體隔振器能帶結構Fig.5 Band structure of isolators with vibration in the vertical direction

由于地鐵減振措施主要針對垂向振動，因此在研究聲子晶體隔振器帶隙特性時，應篩選振動方向為垂向的導波模態[16].篩選后的能帶結構如圖5所示.由圖5可知，聲子晶體隔振器第一帶隙起始頻率fs為 51 Hz，對應的k= π/b；截止頻率fe為 147 Hz，對應的k= 0.波矢即波數矢量，表示單位長度內的波數，波數與波長對應，因此k= π/b對應波長為晶格常數一半的彈性波，k= 0對應彈性波長為無窮大的彈性波，兩個波長下的垂向導波模態即為帶隙的起始與截至模態.

2.2 邊界頻率

為了探究聲子晶體隔振器的帶隙特性，計算了決定第一帶隙邊界頻率的共振模式，如圖6所示.

圖 6 第一帶隙起始頻率共振模態和截止頻率共振模態Fig.6 Resonance modes at start frequency and cut-off frequeny of the first bandgap

由圖6可知，決定起始頻率的共振模式表現為相鄰鋼散射體帶動軟橡膠包覆層發生反相位共振，而基體外殼與橡膠墊層振動較小，整個結構在此共振模式下實現動態平衡，因此起始頻率fs約等于鋼散射體的共振頻率.

2.3 帶隙特性驗證

聲子晶體隔振器振動帶隙的計算是在無限周期的條件下進行的，由于隔振器實際尺寸的限制，而本文中的聲子晶體隔振器實際周期數為3，需利用傳輸特性[17]刻畫其實際隔振效果，對帶隙特性進行驗證.由于聲子晶體隔振器為一維周期結構，故在隔振器上端施加簡諧加速度激勵，計算下端加速度響應，通過式（5）求得聲子晶體隔振器的加速度傳遞率（T），分析其傳輸特性，如圖7所示，圖中，Xin和Xout分別為輸入和輸出激勵.

圖 7 聲子晶體隔振器傳輸特性有限元計算模型Fig.7 Finite element model for transmission characteristics of isolators

式中：aout和ain分別為輸出端和輸入端加速度幅值平均值，以傳遞率數值小于0的限界確定振動傳遞的衰減頻段.加速度傳遞率是利用有限元軟件COMSOL Multiphysics進行計算的，計算結果如圖8所示.

圖8中的虛線和實線分別表示無阻尼和有阻尼（同時包含內層和外層橡膠阻尼）時的傳遞率計算結果.當不考慮阻尼時，振動衰減頻率范圍為51～147 Hz；考慮阻尼時，振動衰減頻率范圍為48～147 Hz.比較圖5和圖8可知，通過能帶結構得到的帶隙頻率范圍和通過傳遞率得到的振動傳遞衰減頻段吻合較好.

圖 8 聲子晶體隔振器頻響函數Fig.8 Frequency response function of isolators

3 聲子晶體隔振器浮置板軌道整體減振效果計算

為了驗證聲子晶體隔振器在浮置板軌道中的減振效果，并且與普通鋼彈簧浮置板軌道的減振性能進行對比，取相同剛度的鋼彈簧與聲子晶體隔振器分別進行計算，進行對比分析.

3.1 聲子晶體隔振器垂向靜剛度

聲子晶體隔振器作為結構部件，需為浮置板道床提供垂向剛度.為了保留傳統鋼彈簧浮置板軌道的隔振效果，聲子晶體隔振器的垂向靜剛度需與鋼彈簧隔振器的垂向靜剛度一致.相關文獻表明[18]，鋼彈簧隔振器垂向靜剛度實測為6.0 kN/mm左右.

本文采用有限元軟件計算聲子晶體隔振器垂向靜剛度.固定約束聲子晶體隔振器下端面，在上端面施加垂向靜荷載F，計算上端面的平均位移D，聲子晶體隔振器垂向靜剛度由表達式F/D而得.

經計算，聲子晶體隔振器垂向靜剛度為6.0 kN/mm，與鋼彈簧隔振器的垂向靜剛度相近.

3.2 聲子晶體隔振器浮置板軌道整體減振效果

圖 9 聲子晶體隔振器浮置板軌道三維軌道模型Fig.9 Three-dimensional floating slab track with isolators

聲子晶體隔振器浮置板整體減振效果為振動傳遞衰減效果和隔振效果的疊加.為了探究聲子晶體隔振器浮置板整體減振效果，本節建立了三維軌道模型，如圖9所示.由于模型沿縱向的長度有限，為了減少反射波對計算結果的影響，在鋼軌和浮置板的兩端施加低反射邊界條件.在整個模型正中位置處的跨中鋼軌軌頭施加簡諧垂向力Fin=F0eiωt（F0為垂向力的幅值），經計算提取最近聲子晶體隔振器傳遞至下部基礎的力Fout.通過計算力傳遞率（force transfer rate，

FTR）rFTR來反映聲子晶體隔振器浮置板軌道整體減振效果：

當力傳遞率較小時，浮置板軌道即有著較好的減振效果.采用有限元法求解上述模型，所有軌道部件均采用實體建模，劃分的有限元模型如圖10所示.

圖 10 有限元模型網格Fig.10 Finite element meshing of the model

同樣，本節對傳統浮置板軌道建立了三維軌道模型，計算其力傳遞率，用以對比聲子晶體隔振器浮置板軌道的計算結果.計算時，鋼彈簧隔振器采用彈簧單元模擬，垂向剛度為6.0 kN/mm，這與聲子晶體隔振器垂向靜剛度相同.上述模型的計算參數如表2所示.

聲子晶體隔振器浮置板力傳遞率計算結果如圖11所示.由圖11可知，兩條力傳遞率曲線均在25 Hz處與97 Hz處出現波峰，這是因為此頻率下浮置板軌道發生彎曲共振.當頻率高于25 Hz，兩種軌道結構的力傳遞率隨著頻率的增大而逐漸減小.由于聲子晶體隔振器和鋼彈簧隔振器的垂向靜剛度相同，38 Hz以下的力傳遞率幾乎一致.

表 2 模型計算參數Tab.2 Model calculation parameters

圖 11 力傳遞率計算結果Fig.11 Calculation results of force transmissibility

為了進一步評價聲子晶體隔振器與鋼彈簧浮置板軌道的減振效果，建立考慮基礎參振的動力學模型進行同樣沖擊荷載作用下的減振性能對比分析，軌道部分模型材料參數與邊界條件同上述整體軌道模型，仰拱部分參數如表3，為了加快計算效率，整體模型采取軌道結構的一半，采用對稱邊界條件，整體模型示意圖如圖12.

在整個模型正中位置處的跨中鋼軌軌頭施加脈沖荷載，經計算提取最近聲子晶體隔振器傳遞至下部基礎的振動.通過對比聲子晶體隔振器浮置板軌道與鋼彈簧浮置板軌道傳遞至下部基礎的加速度來評價其減振性能，圖13（a）為下部基礎振動加速度時域計算結果對比，圖13（b）為下部基礎振動加速度頻域結果的對比.

表 3 仰拱部件計算參數Tab.3 Calculation parameters of invert components

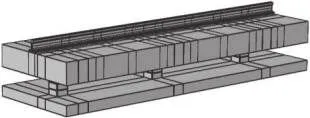
圖 12 考慮基礎參振的整體計算模型Fig.12 Overall calculation model with base vibration

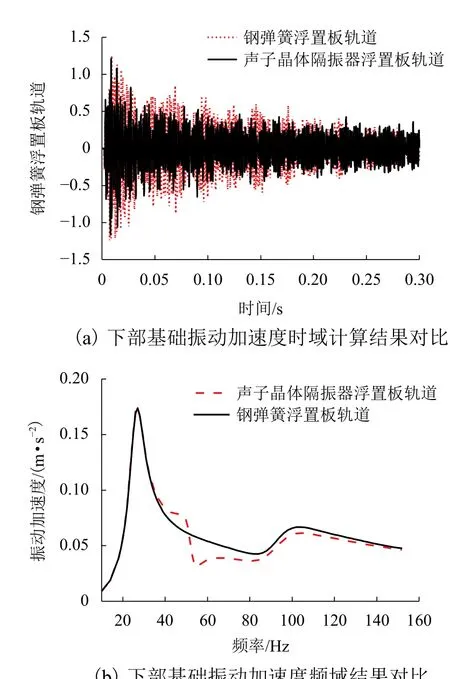
圖 13 下部基礎振動加速度時頻域計算結果Fig.13 Frequency-domain results of the vibration acceleration for lower base

由圖13（a）可知，聲子晶體隔振器浮置板軌道下部基礎的振動加速度在大多數時間段內小于鋼彈簧浮置板下部基礎的最大振動加速度，說明聲子晶體隔振器浮置板軌道具有一定的減振效果；由圖13（b）的頻域結果可知，在51～150 Hz帶隙范圍內，相比普通鋼彈簧浮置板軌道具有更好的減振效果，且在51 Hz附近，減振效果最佳.

由于聲子晶體隔振器具有振動傳遞衰減特性，在50～129 Hz頻率范圍內，聲子晶體隔振器浮置板軌道的力傳遞率低于傳統浮置板軌道，說明其減振效果得以加強.在51 Hz處聲子晶體隔振器與傳統鋼彈簧浮置板力傳遞率相比，可減小10 dB左右，在整個聲子晶體帶隙范圍內，有60%頻帶范圍內相比鋼彈簧浮置板可減小2 dB以上.且聲子晶體隔振器可以通過參數優化，實現對減振效果增強頻率范圍的精準控制.

4 結 論

本文提出了一種基于局域共振帶隙機理的聲子晶體隔振器，并將其應用于地鐵浮置板軌道結構中.本文主要結論如下所示：

（1）聲子晶體隔振器第一帶隙的起始頻率主要由鋼散射體的共振決定，截止頻率主要由鋼散射體與軟材料和基體材料所組成的聯合體的反相位共振決定；

（2）聲子晶體隔振器所提供的垂向剛度與第一帶隙頻率范圍是相互獨立的；聲子晶體隔振器的振動傳遞衰減特性以及帶隙頻率范圍可以通過修改材料進行控制，從而可以滿足更多工程的減振需求；

（3）將聲子晶體隔振器與鋼彈簧分別應用于浮置板軌道計算其力傳遞率與基礎的振動加速度，表明新型浮置板軌道相比傳統鋼彈簧浮置板軌道，可提供與傳統鋼彈簧相近的垂向剛度，在保留傳統鋼彈簧浮置板軌道低頻隔振性能的前提下，進一步抑制低頻帶隙頻率范圍內縱波從道床板向基底的傳播，與傳統鋼彈簧浮置板力傳遞率相比，在51 Hz左右可減小10 dB左右，帶隙其余大部分可減小2 dB左右.

致謝：感謝廣州地鐵設計研究院股份有限公司“基于聲子晶體理論的新型減振降噪措施理論與試驗研究”研發項目支持.