基于Black-Litterman模型對我國股票市場的資產配置研究

趙心

摘 要：本文基于Black桳itterman框架以上證50的股票數據為基礎，運用ARMA桮ARCH模將投資者主觀觀點與資產的先驗收益相結合，進而通過實證可以得出BL模型的預期收益普遍高于市場的均衡收益，在此基礎上確認不同收益率下的投資組合權重，得到投資組合的有效前沿以及不同資產配置下的夏普比率，為投資者決策提供參考。

關鍵詞：投資組合;資產配置;B-L模型

一、 引言

馬科維茨的均值――方差模型是最早的投資組合理論，但令人遺憾的是，均值――方差模型雖然在數學上非常直觀明了，但在投資實務中卻存在著模型的輸入參數期望收益率異常敏感的問題。為解決這一問題，1992年高盛的Fischer 和Robert 提出了Black桳itterman資產配置模型（簡稱BL模型）。該模型分別輸出投資者對資產的觀點和市場的均衡收益，根據貝葉斯方法將先驗的收益和觀點結合，得到后驗的預期收益，求解二次規劃得到最優的資產配置權重。

對BL模型的研究主要集中在觀點收益向量和觀點誤差矩陣的預測。如溫琪，陳敏等人基于GIR桮ARCH模型來預測收益率和方差;閆亞萍將美林“投資時鐘”和BL模型相結合以及殷鑫鑫將風格輪動和BL模型相結合進行資產配置。本文基于賈慧提出的ARMA桮ARCH模型，通過GARCH模型輸出的預期收益來代表投資者觀點，協方差代表觀點誤差矩陣，代入BL模型求出后驗收益率，與市場的均衡收益率進行比較的同時求解二次規劃得到最優的投資組合權重。

二、 基于ARMA桮ARCH模型的實證分析

1.數據選取與檢驗

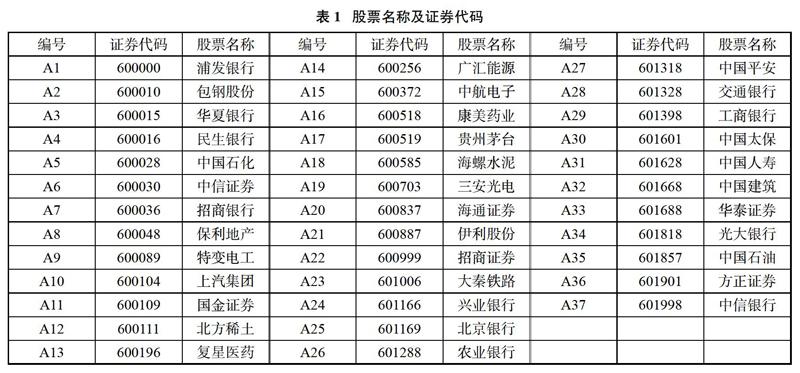
（1）數據選取。本文從上證50的50支成分股剔除了13支數據缺失較大的股票，最終留下37只股票（周收益率），數據來源于WIND.數據區間為2014年1月10日至2018年12月28日，貫穿了一個牛熊的輪回，經歷了較為完整的市場周期，可以較全面的反應滬市的波動率特征。具體的股票選擇情況如表1所示。

（2）描述性分析。基于周收益率，我們分別繪制了37只股票的時序圖和QQ圖.限于篇幅，暫且省略了相關圖表，根據時序圖的描述結果可得各股票收益率序列呈現出一定的波動集聚性，大的波動后面跟著小的波動.由QQ圖可以得到各股票周收益率不服從正態分布，且尾部的散點偏離直線較明顯，顯示出厚尾特征。

對上證50的37只股票的描述性統計可以得出各股票周收益率序列的峰度普遍大于3，偏度均異于0，呈現右偏或左偏的分布現象;JB統計量均在1%的顯著性水平下大于0，說明收益率序列不服從正態分布。

（3）平穩性檢驗。基于R語言，本文對37只股票的周收益序列進行平穩性檢驗（滯后12階）。結果顯示各股票周收益率序列的ADF統計量均5%顯著水平下的數值，P值均小于0.01，故拒絕存在單位根的原假設，即各股票周收益率序列為平穩序列。

（4）相關性檢驗。對所選股票進行相關性檢驗，以A1桝4為例。A2的自相關系數存在著部分超出兩倍的估計標準范圍，A1、A3和A4除個別自相關系數觸及兩倍的標準線外，大部分落在兩倍的估計標準范圍內，同時結合Ljung桞ox檢驗的Q統計量和對應的P值，可以得出A2的周收益率序列存在顯著的前后相關性，A1、A3和A4的相關性較弱。

2.GARCH模型的實證分析

（1）ARMA模型及白噪聲的建立。基于上述股票周收益率序列的相關性，本節建立ARMA模型。以A2和A3為例。我們對A2建立ARMA模型，根據擬合效果，ARMA（3，2）的系數高度顯著，AIC和SC準則的值相比之下也是較小的。模型擬合結果為：

通過殘差平方序列自相關檢驗，我們可以得到，A2的自相關圖出現了“拖尾”現象，初步判斷存在ARCH效應。為避免疏忽，對上述模型采用ARCH桳M檢驗，檢驗得LM統計量為32.073，對應的P值為0.00138。因此原序列存在ARCH效應，與自相關檢驗的結論一致。

基于A3的不相關性，將均值方程設定為白噪聲，同時對A3周收益率序列的殘差平方進行相關性檢驗。設立模型為：

根據所描繪的殘差平方的自相關圖可以看出A3殘差的平方序列存在自相關。LM統計量為43.65，對應的P值為0.00001752，存在很強的ARCH效應。

（2）建立GARCH模型。由于上述殘差序列均存在條件異方差，因此考慮建立GARCH模型來消除異方差。我們可以得到A2和A3的GARCH模型方程：

對擬合后的模型進行條件異方差檢驗，結果如表3所示，可以看出兩個股票對應的F統計量和LM統計量所對應的伴隨概率P值均顯著大于0.1，表明其接受不存在ARCH效應的原假設。

用類似的方法，我們可以得到本文37只股票的殘差序列均存在ARCH效應，對其分別建立GARCH模型均可消除其條件異方差性，得到37只股票的周收益率情況和條件方差作為BL模型的輸入參數。

3.Black―Litterman模型構建與實證分析

（1）BL模型簡介。BL模型的構建是先基于超額收益的協方差矩陣∑，流通市值權重，以及風險厭惡系數，得出均衡投資組合的隱含收益率∏，進而得出先驗的均衡收益分布;基于觀點向量Q和投資人觀點誤差矩陣 ，得到我們的觀點收益分布。將二者相結合，基于貝葉斯方法我們可以得到預期收益：

將求解出的預期收益率代入到下面的均值方差模型中，求解最大效用：

通過逆最優化求解二次規劃，得到我們想要的投資組合權重。

（2）市場均衡收益。首先基于∏= ∑求解我們的均衡收益，其中風險厭惡系數由公式 =來計算，和分別代表市場收益率和無風險收益率， 2是市場收益率的方差。本文以2014？018年同時期的50指數的周收益率和方差來計算，用十年期國債的收益率3.13%來表示無風險利率。由于2014年股市的波動，我們調整了14年股市的收益率權重，最終算出的風險厭惡系數 =3.48。進而代入公式求解出我們的市場均衡收益。結果如下：

（3）觀點收益向量和觀點誤差矩陣。基于GARCH模型預測的周收益率和上述市場的無風險利率，我們可以得出超額收益率=輸出觀點收益向量Q，結果如下：

觀點誤差矩陣 基于GARCH模型求出的條件方差來表示。

（4）主觀觀點矩陣和信心水平。主觀觀點矩陣P通常有兩種形式，相對觀點和絕對觀點。本文簡化起見，采用絕對觀點，以37階單位矩陣來代表投資者對每只股票的觀點。標量 代表投資者對所持觀點的信心程度。本文采用Idzorek等人的觀點，分別選取了0.01、0.05、0.1進行對比分析，經過實證結分析可以得出隨著信心水平的提高，各股票的預期收益隨之上升，因此為了得出更理想的結果，本文最終選擇 =0.01。

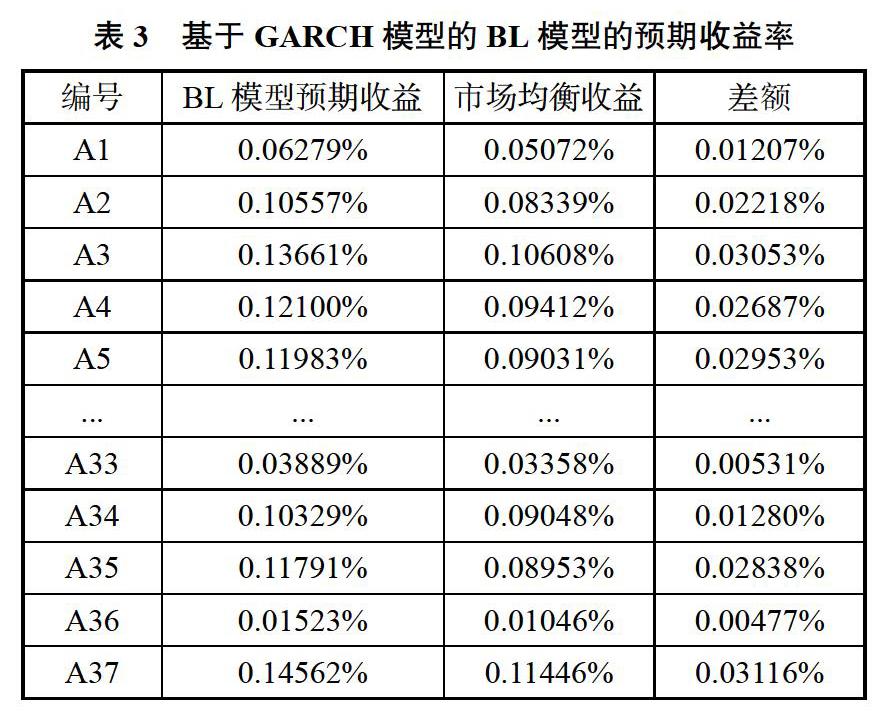
（5）BL模型預期收益率與最優投資組合。根據上述公式1中的預期收益E（R），將相關參數代入公式中，通過矩陣運算得出求解的BL模型的預期收益，如表3所示。

比較上表的BL模型預期收益和市場均衡收益我們可以看出，基于GARCH模型收益率和條件方差預測的收益率普遍高于市場收益率。與此同時，BL模型較均值方差模型而言，有效地避免了因個股收益的細微變動而產生的巨大變動，能夠為投資者提供更加穩定的投資組合。

在這種情況下，我們基于預期收益率，通過調用R軟件中的fportfolio包，我們計算得對應得投資組合得權重、協方差和在險價值。

由表4我們可以得出，對BL模型進行資產權重配置時，收益率為0.0013時，配置較為分散，重點配置在A1、A14、A35、A36;收益率為0.0036時，重點配置A7、A17、A25、A36;收益率繼續上升時，股票權重配置的個數越來越少，收益率為0.006時，重點配置A7、A17兩只股票;當收益率達到0.0083時，A17的配置權重達到了1。同樣的觀察協方差和在險價值，除了收益率為0.0011外，在收益率為正的情況下，我們可以看到，隨著收益率的上升，協方差和在險價值也隨之提高。符合我們的一般假定，收益越高，伴隨的風險也越大。

在得到BL模型的預期收益率的情況下，我們基于R語言得到了投資組合的有效前沿。其中，中心區域的點代表著蒙特卡洛模擬的資產組合，與有效前沿相切的線代表著資產配置先，與之對應的中間的藍點代表著等權重的資產組合，藍色的曲線代表著不同投資組合的夏普比率。可以看出，當資產組合的目標收益率為大約0.003，風險最小為大約0.020時，當投資組合的目標收益率接近0.008時，投資組合的風險達到了0.0045。據此，結合投資組合的有效前沿和夏普比率線等，為投資者的風險投資決策提供參考。

三、結論

本文基于Black―Litterman模型的基礎上提出了一個股票配置策略。選用ARMA―GARCH模型來擬合上證50的37只股票的收益率和波動率，將預測的收益率和波動率加入BL模型中，來計算投資組合的資產配置，并得到資產配置的有效前沿和夏普比率。研究結果表明：投資者信心水平的差異會造成BL模型的預期收益率向量有所不同，同時投資者的信心水平越大，BL模型的預期收益與市場均衡收益的差值越小，越接近市場均衡收益。另外，加入投資者觀點的BL模型的預期收益率普遍高于市場的均衡收益率，隨著收益的增加，投資組合會越發地集中于所選取股票池中的幾只甚至一只股票。

參考文獻

1.Black And Litterman.Global Portfolio Optimization. Journal of Fixed Income，1991.

2.賈慧.Black-Litterman模型在中國股票市場資產配置中的應用研究.西北大學，2011.

3.吳睿.Black-Litterman模型在證券資產配置中的應用研究.遼寧大學，2016.

（責任編輯：王文龍）