超快激光加熱薄膜的格子玻爾茲曼模擬

毛煜東呂慧麗孫浩森陳明九于明志

(山東建筑大學熱能工程學院，山東濟南250101)

0 引言

近年來，激光加熱技術已展現出強大優勢，并廣泛應用于激光焊接、激光鉆孔、激光熔覆、激光照明、三維印刷技術以及熔化動力學等諸多領域[1-5]。由于該技術具有高效率、高功率密度、最小的附帶材料損壞、較低的燒蝕閾值等優點而受到了越來越多的關注。目前該技術在材料的熱加工過程中具有很好的應用，如激光清洗、激光圖案化以及超音速激光沉積等[6-8]。現代微加工技術要求微結構的高精度加工生產能力，以及材料熱處理中加熱時間迅速和位置的高精度控制，探索微結構的傳熱過程是十分重要的。1822年，傅立葉經實驗研究導熱過程并對其歸納總結，得到了描述宏觀導熱過程的基本定律—傅立葉導熱定律，并逐步地應用到了機械、冶金、建筑以及電氣等領域[9]。然而，傅立葉定律暗含熱以擴散的方式傳播且熱傳播速度無限大，即如果對導熱體內某一點施加熱擾動，則其他部分會同時感受到此熱擾動帶來的溫度變化，即傅立葉定律忽略了熱傳導過程中溫度梯度和熱流矢量之間的弛豫時間。

玻爾茲曼輸運方程BTE(Boltzmann Transport Equation)用于解決微尺度系統中的熱輸運問題[10]是十分有效的手段。BTE是統計力學中用以描述不平衡態分布函數演化規律的方程，但BTE中含有的碰撞算子項是一個非常復雜的非線性微分積分，極難以求解。格子玻爾茲曼方法 LBM(Lattice Boltzmann Method)是BTE常用的數值解法之一，LBM依據非平衡統計力學的運動論，在解決邊界，實現編程和處理復雜的多尺度耦合問題方面具有明顯的優勢，是求解BTE的有效手段，受到了廣泛的關注[11-12]。基于LBM而來的格子BGK模型LBGK(Lattice Bhatnagar-Gross-Krook)簡化了BTE中的碰撞算子項，用弛豫時間近似表達了不同粒子間的碰撞達到的復雜機制，并且不考慮外力的影響。由于計算效率高，能精準地推導出納維—斯托克斯方程N-S(Navier-Stokes equations)，常用于研究不可壓縮流體和微尺度的導熱問題，也是LBM主要的研究模型。

近年來，LBM廣泛應于描述微納米尺度傳熱的問題中。Escobar等[13]應用LBM研究了一維半導體材料中的瞬態多空間尺度和時間尺度的導熱過程，與基于擴散-彈道輸運方程、傅立葉導熱方程和CV模型的結果做了對比，并對主要的導熱模型的使用范圍做了簡要總結。華鈺超等[14]用熱質理論的觀點分析了彈道擴散導熱機理，基于聲子玻爾茲曼方程推導了修正邊界條件模型，數值求解了修正的普適導熱定律，并與蒙特卡羅模擬進行對比。張珂等[15]基于LBM和雙曲兩步模型結建立了一個LBM兩步方程，并利用此方法模擬研究了納米薄膜在超快激光照射過程中的熱響應特性，分析了照射過程中薄膜內溫度隨時間及空間的變化規律，探討了激光強度以及薄膜厚度對金屬薄膜熱響應的影響。文章應用LBM方法對超快速激光加熱硅薄膜的一維導熱問題進行研究，來描述這種時間超短，尺寸超小的超快速納米傳熱問題，展示薄膜內部能量密度分布情況，并對結果進行分析。

1 理論分析

LBGK模型的表達式由方程(1)表示為

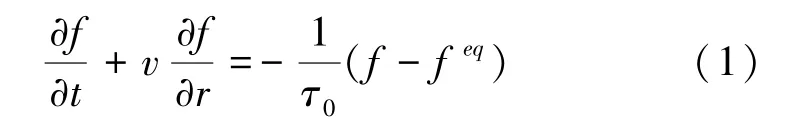
式中:f(r，ξ，t)為分子速度分布函數；r為空間位置矢量；ξ為分子速度矢量；t為時間參數；feq為熱力學平衡態時的速度分布函數；v為熱載子的群速度；τ0為松弛時間(也叫弛豫時間)是粒子發生2次碰撞的時間間隔，表征粒子碰撞后達到平衡態的快慢程度。

1.1 LBM方法驗證

傅立葉導熱定律可以很好地描述宏觀問題，文章采用LBM方法解決微觀—宏觀問題，應先驗證LBM在解決宏觀熱傳導問題時的有效性。建立一個簡單的薄膜導熱問題，即在薄膜左側施加一個無量綱數為1的熱擾動，其控制方程由式(2)表示為

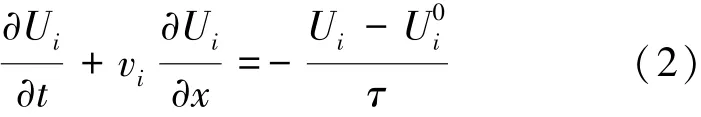
式中:Ui為能量密度；x為位置參數；U0i為平衡能量密度；vi為聲子群速度；τ為聲子弛豫時間。

考慮常溫初始條件，將式(3)～(6)所示的無量綱變換為

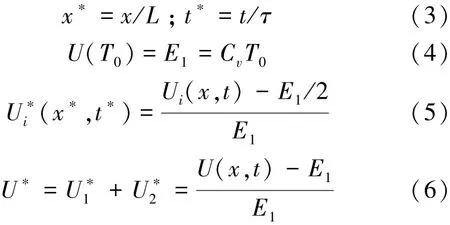
式中:x?為無量綱位置參數；L為薄膜的特征長度；Cv為硅的體積熱容；t?為無量綱時間參數；U?為無量綱能量密度參數；U1?為向x軸正方向傳輸的無量綱能量密度；為向x軸負方向傳輸的無量綱能量密度；T0為初始時刻溫度；E1為初始溫度T0下的能量。

在做與式(3)～(6)相同的無量綱變換后，其邊界條件由式(7)表示為

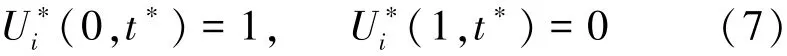
1.2 應用LBM模擬超快激光加熱薄膜問題

建立基于LBM的一維熱傳導模型來模擬超快激光在硅薄膜中的能量分布。在硅薄膜中，聲子是主要的能量載體。基于BTE，考慮超快激光加熱薄膜問題的一維導熱模型由式(8)表示為

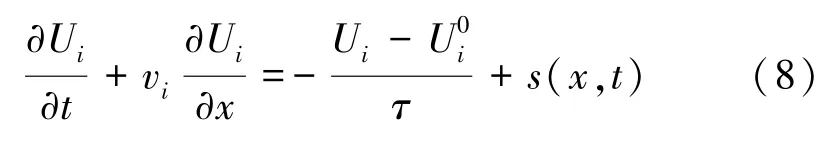
式中:i=1，2；S為能量吸收率，可由式(9)[16]表示為

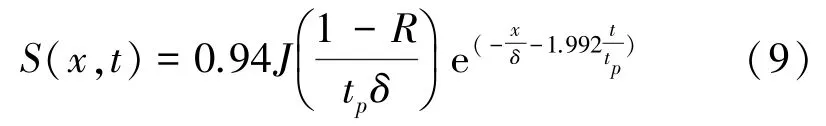
式中:J為激光能量發射密度；R為表面反射率；tp為激光脈沖的持續時間；δ為激光穿透深度。

使用LBM離散式求解方程(8)，忽略高階項，并做與式(3)～(6)相同的無量綱變換后，則主導方程可由式(10)和(11)表示為

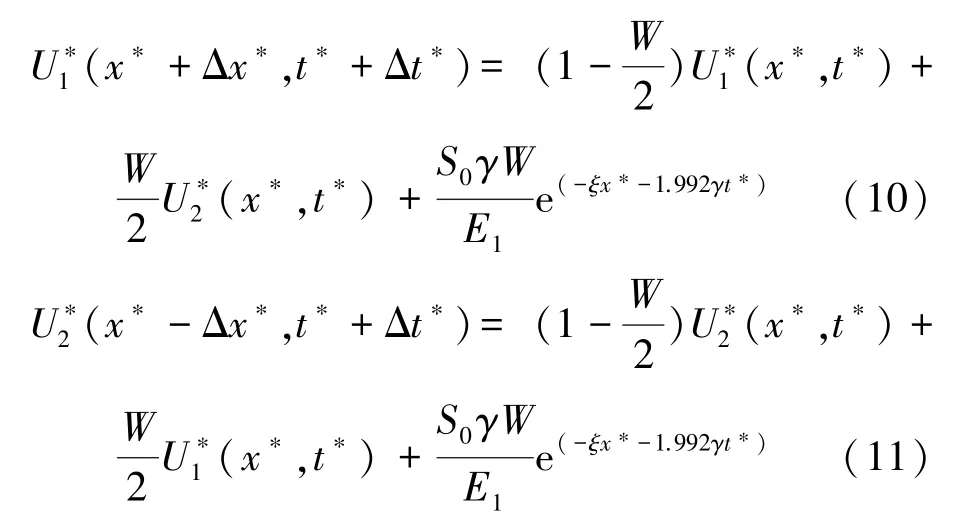
式中:W=Δt?=Δx?/Kn；ξ=L/δ；γ=τ/tp；W、ξ、γ均為中間參數，無特殊含義Kn=l/L為克努森數；l為聲子平均自由程。

根據傅立葉定律，將上述的超快激光加熱問題由經典熱傳導方程式進行描述，由式(12)表示為

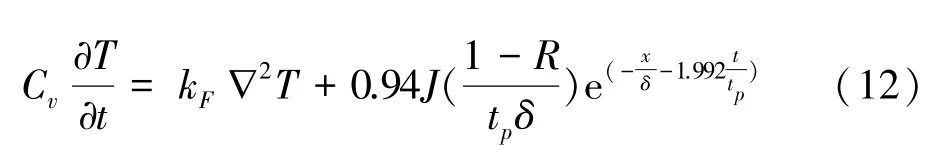
式中:kF為硅的導熱系數。

基于相同邊界條件，可將函數的解展開，由式(13)～(15)表示為

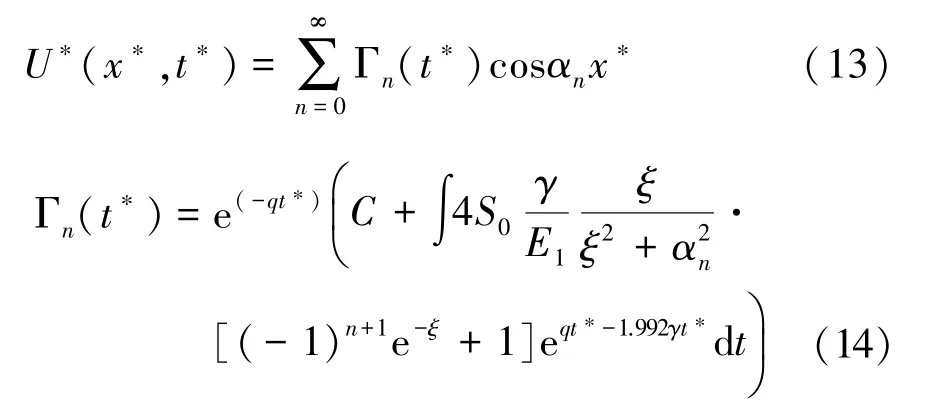
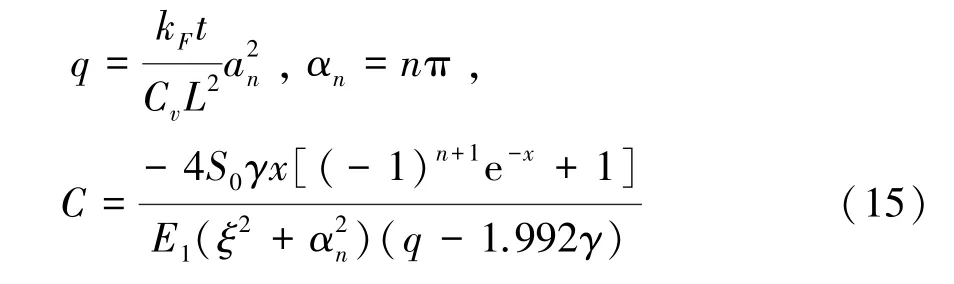
1.3 應用LBM模擬雙側超快激光加熱薄膜問題

利用相同的超快激光脈沖同時從硅薄膜的兩側表面進行加熱，并設置與單側加熱相同的鏡面反射邊界條件和常溫初始條件。此時描述該問題的BTE控制方程由式(16)～(18)表示為

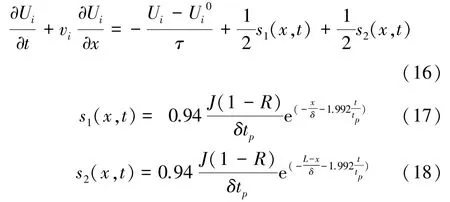
將式(17)和(18)代入式(16)中，可將控制方程變為式(19)形式

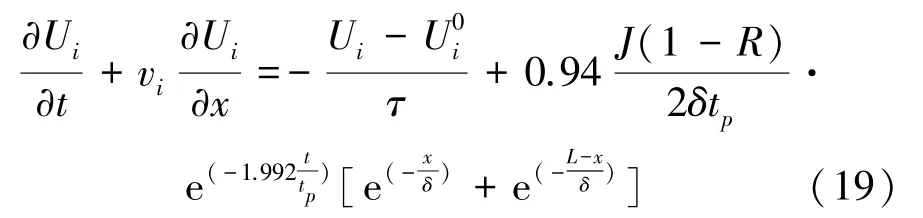
利用LBM對式(19)進行離散求解，方法與式(10)和(11)相同，不再贅述。

2 數值結果與分析

為便于分析，超快脈沖激光加熱的硅膜采用以下參數:體積熱容Cv為1.66×106J/(m3·K)，硅的聲子平均自由程l為41 nm，聲子弛豫時間τ為6.53 ps，持續時間tp為 0.65 ps，激光通量J為312 J/m2，穿透的光學深度δ為15.3 nm，以及激光的表面反射率R為0.93。

2.1 驗證LBM在微觀—宏觀問題的有效性

分析式(2)～(7)描述的薄膜導熱問題，分別利用LBM和經典傅里葉熱傳導理論對該問題進行求解和模擬，觀察薄膜內部的能量傳遞現象，如圖1所示。可以看出，通過LBM獲得的結果清楚地表現出擴散行為，并顯示出良好的擴散性能，這與傅立葉導熱理論所給出的結果一致。因此，LBM可用于模擬宏觀擴散狀態下的熱傳導。

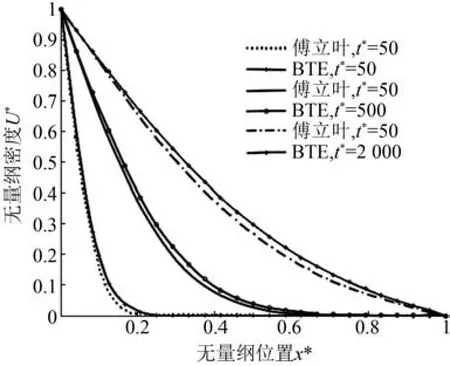
圖1 利用LBM和傅立葉定律得到的Kn=0.001的無量綱能量密度分布圖

改變克努森數，將熱傳導過程引入到過渡區，并觀察LBM和傅立葉定律得到的結果之間的差異，如圖2所示。當克努森數為1時，此時薄膜內熱傳遞處于過渡區，基于LBM和傅立葉定律的解決方案表現出截然不同的行為。可以看出，當無量綱時間為0.1時，通過LBM模擬獲得的能量密度分布具有顯著的特征:能量密度在受加熱側(左側)邊界有明顯的跳躍；隨著時間的流逝，由LBM獲得的熱能以熱波的形式在薄膜內部傳輸；當t?達到1時，能量密度又在右側邊界發生了的躍變。然而，傳統的傅立葉定律卻不能捕捉這一現象，由于其內含熱傳遞速度無限大的假設，在過渡區，薄膜內任何一處都可以立即感受到受加熱側施加的熱擾動。

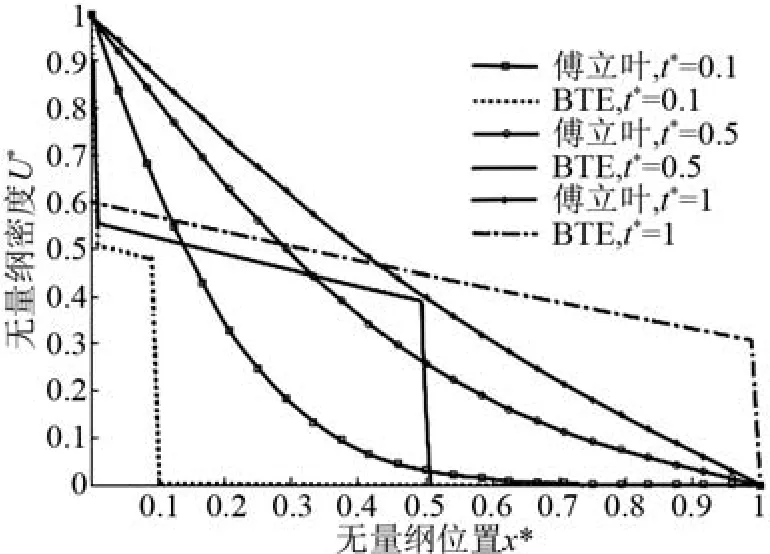
圖2 利用LBM和傅立葉定律得到的Kn=1的無量綱能量密度分布圖

2.2 單側激光加熱納米薄膜導熱問題

分析式(8)和(9)所描述的利用超快激光加熱厚度為82nm薄膜的導熱問題。通過傅立葉定律和LBM方法得到的無量綱能量密度分布如圖3所示。從圖3(a)中可以看出，基于傅立葉定律的熱傳導是一個擴散過程。由于強大的激光脈沖加熱，短時間內能量密度就在薄膜的左側區域迅速向右側擴展。隨著時間的流逝，能量密度逐漸降低，并最終在薄膜內趨于穩定。

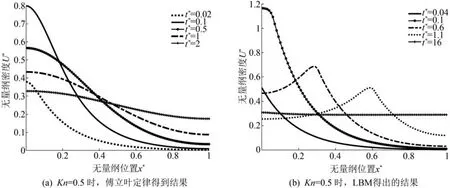
圖3 激光加熱薄膜單側時薄膜內無量綱能量密度分布圖

然而，對于相同的加熱問題，LBM卻得到了不同的結果，如圖3(b)所示。在初始階段，同傅立葉定律獲得的結果相比，受到脈沖激光擾動的左邊界附近產生了更高的能量密度。該無量綱密度峰值達到了1.18，較傅立葉結果的0.8相比，超出約47.5%。這表明，傳統的傅立葉熱定律在描述這此類微納米尺度下的超快加熱問題時會嚴重低估熱載子傳輸的最大能量密度。

隨著時間的流逝，薄膜內部能量是以波的形式從左端傳遞到右端，且隨著能量波的傳遞，其能量密度峰值逐漸下降，這一現象并未出現在傅立葉定律得出的結果中。LBM的結果還發現，在鏡面反射的邊界條件下，能量密度會經過一個較傅立葉結果更為漫長的時間后才能在薄膜內趨于穩定。

2.3 雙側激光加熱納米薄膜導熱問題

分析式(16)～(19)所述利用相同的超快激光脈沖同時從硅薄膜的兩側表面進行加熱的問題。在克努森數為0.5時，利用傅里葉定律和LBM方法得到的薄膜內部的能量密度分布情況如圖4所示。如同預期的那樣，傅立葉的結果顯示了熱傳導的擴散行為，也并未發現能量波狀傳遞的行為，如圖4(a)所示。初始時刻，左右兩側的無量綱能量密度峰值均為約0.8，同單側激光加熱時相同，經過無量綱時間2后，薄膜內部能量密度達到穩定，此時無量綱能量密度值為0.5。

由圖4(b)可以看到，在初始時刻受激光脈沖擾動的兩個邊界附近的區域能量密度的快速升高(即溫度快速提升)；隨后，從左右邊界發起的2組熱波從不同方向同時向硅膜的中間區域傳輸，在此期間，能量密度峰值逐漸降低。當無量綱時間達到1時，2組熱波峰在薄膜的中間區域匯合，相互的碰撞作用導致了薄膜中心區域的能量密度顯著升高。此時，在中心點處的能量密度的峰值為1.095，約為圖3(b)所示的單側激光加熱情況下所預測的峰值的兩倍，這一現象不僅是傅立葉結果無法捕捉的，而且在單側激光加熱時也不會出現。最后，當無量綱時間達到16時，薄膜內能量密度趨于穩定；相比于傅立葉結果，在鏡面反射的邊界條件下，趨于穩定所需時間要更為漫長。

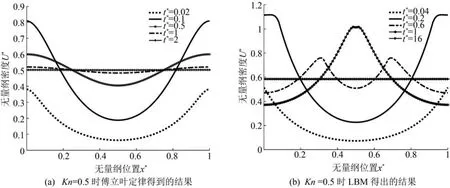
圖4 激光加熱薄膜兩側時薄膜內無量綱能量密度分布圖

3 結論

文章應用LBM方法和傅立葉定律對超快激光加熱硅薄膜的一維導熱問題進行研究，分析了薄膜內部能量密度分布情況。主要結論如下:

(1)發現在克努森數較小的連續介質區，LBM得到的結果符合傅立葉定律給出的結果；然而在系統特征尺度和分子平均自由程相當的過渡區，LBM方法可以捕獲到能量以波動的方式進行傳輸的熱波特性，但傳統的傅立葉定律無法得到。

(2)利用LBM數值模擬激光加熱硅薄膜的一維導熱問題，發現克努森數對薄膜內無量綱能量密度的分布具有重要的影響。

(3)如果利用超快激光分別在薄膜的兩側進行加熱，薄膜內部的能量密度分布情況將有所改變，尤其是當沿相反方向傳播的兩個熱波交匯在一起時，會發生碰撞并使得能量密度有顯著的提升，這些現象均在傅立葉定律結果中不能呈現。此外，研究發現傳統的熱傳導理論可能嚴重低估了過渡區聲子輸運的最大能量密度。