地鐵車輛運行對周圍土體與建筑影響的研究

關天偉魏煥衛

(山東建筑大學土木工程學院，山東濟南250101)

0 引言

近年來，隨著城市地鐵工程的不斷發展，列車荷載導致的隧道結構—土體以及地面振動問題越來越引起人們的重視。地鐵運營期間，隧道周圍土體在列車循環荷載作用下會產生砂土液化、不均勻沉降和地面塌陷等問題，影響地鐵的安全運行以及地鐵沿線構筑物的正常使用。對此，許多學者都做過相關研究。楊文波等[1]采用頻率響應函數FRF分析了盾構隧道與周圍土體不同位置處的動力響應及衰減規律；劉濤[2]研究了地鐵動荷載作用下黃土地區隧道振動響應分析；范思婷等[3]采用實測數據，對隧道內列車運行引起的鋼軌、軌枕和隧道壁振動進行了分析；閆維明等[4]研究了某地鐵運營引起的地面振動實況和特性及振動傳播規律；馬蒙等[5]運用半空間位移格林函數解析解對地表振動局部放大現象進行了分析；張曦等[6]對上海地鐵二號線進行連續動態監測，對振動荷載作用下飽和軟黏土的響應頻率、土體響應應力幅值隨深度的變化規律進行研究；Tsuno等[7]提出了一種地鐵振動離心模型試驗系統，比較了振動加速度的實測值與觀測值；樓夢麟等[8]實測了地鐵某區段地面振動，對不同測點的水平、豎直方向加速度衰減規律進行了分析；Gupta等[9]通過倫敦地鐵Bakerloo線的地下試驗對地鐵振動預測的周期性有限元—邊界元耦合模型進行了驗證；鄭國琛等[10]建立了一種有限元模型，對地鐵運行后臨近建筑物的振動響應作出了理論預測。在地鐵動荷載的研究中，列車荷載的模擬方法是研究的重點與難點。李軍世等[11]采用有限元分析法，分析了車速及車輛振動帶來的影響；梁波等[12]用一個疊加的激振力來模擬列車豎向動荷載，探討了路基在不平順條件下的動態響應；張碧[13]和薛闊等[14]采用正弦激勵函數模擬列車荷載，研究了動力響應計算中列車荷載模擬方法的可行性。

上述研究對列車振動荷載的研究集中在動荷載的表達形式上，缺少對臨近土體沉降變化的定性分析。因此，文章采用與不平順管理標準相對應的激振力函數表示列車振動荷載，在此基礎上進行數值模擬，分析隧道周圍土體與建筑在列車振動荷載下的沉降特性，為研究地鐵運營產生的影響提供參考。

1 地鐵車輛動力模型建立

1.1 動荷載的確立

為討論列車動荷載對路基動力反應的影響，采用能夠反映其周期性的類似激勵形式的力表達動荷載。在車輛軸重、軌道不平順、車輛行駛速度、列車振動荷載的周期性等影響因素中，軌道不平順是列車振動荷載的主要影響因素。對于控制條件分別為行車平穩性、動力附加荷載、波形磨耗的軌道不平順管理值見表1。

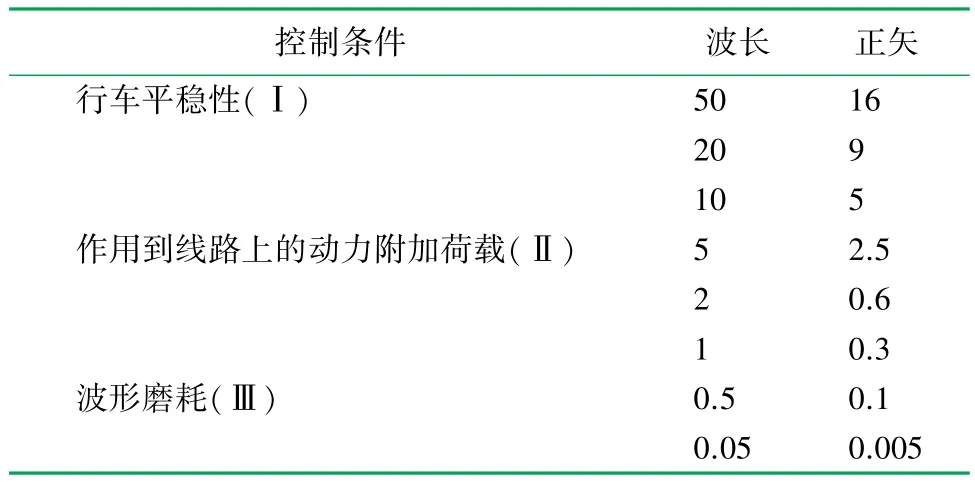
表1 軌道不平順管理值表/mm

采用低、中、高頻對應的波疊加的函數形式模擬列車荷載。荷載計算由式(1)[15]表示為

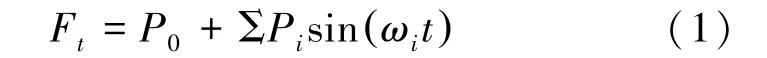
式中:Ft為列車振動荷載，kN；P0為車輪靜載，kN；Pi為對應不平順條件典型值的振動荷載，kN；ωi為荷載振動圓頻率，rad/s；t為列車運行時間，s。

式(1)中荷載Pi和頻率ωi分別由式(2)和(3)表示為

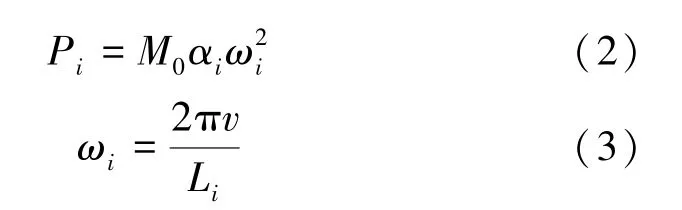
式中:M0為列車簧下質量，kg；αi為相應于表1中Ⅰ、Ⅱ、Ⅲ等3種情況下的某一典型矢高，mm；v為列車車速，m/s；Li為對應于表1中不平順管理值的波長，mm。

式(1)把列車荷載作為集中荷載直接作用于軌道道床表面。在實際情況中，每組輪載都是經過鋼軌、軌枕的傳遞后到達道床表面的，而上述公式并未考慮軌道對列車荷載的分散與傳遞作用。對此，文獻[12]中引入傳遞系數與分散系數，將式(1)修改成式(4)為

式中:k1為傳遞系數，一般取1.2～1.7；k2為分散系數，一般取 0.6～0.9。

1.2 模型參數

采用Plaxis3D有限元軟件進行模擬，假定地基沿橫斷面均勻分布。土體模型的長、寬分別為80、60 m，底部埋深為-30 m。初次模擬時，隧道中心點埋深h0為-9 m，地層結構分為2個不同的土層，第1層為厚度12 m的黏土，第2層為厚度18 m的粉質黏土；隧道模型襯砌管片內、外徑分別為7.2、8 m，不考慮水位因素。建筑物長度b、寬度l2分別為36和12 m，與隧道中心點水平距離l1為8 m。觀測點的位置選取在隧道下方土體沉降最大處及建筑物所在地表，用以分析周圍土體及建筑物所在地表由地鐵列車動荷載產生的沉降值。在隧道下方土體埋深為-13～-17 m的范圍內，每隔1 m選取一個觀測點，分別為A、B、C、D、E；在建筑物地表距隧道近點、中點、遠點分別選取3個觀測點S1、S2、S3，土體位移取向下為正值。建立隧道模型剖面圖如圖1所示。

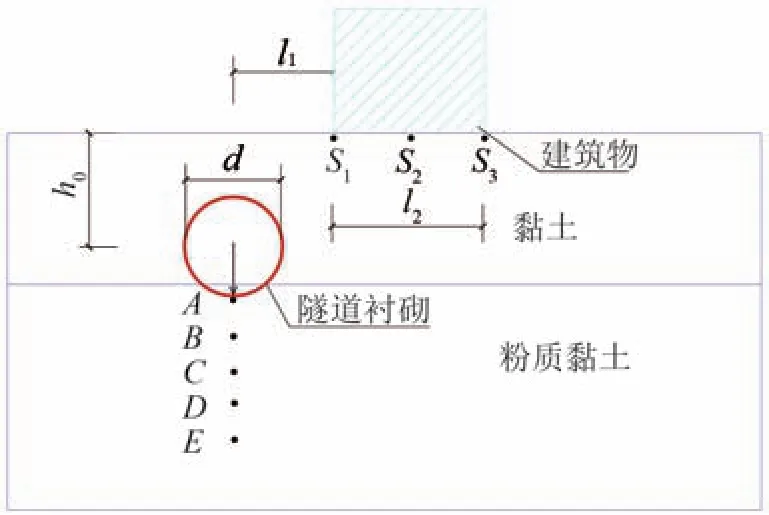
圖1 隧道模型剖面圖

土體本構模型選取摩爾庫倫彈性模型，土層的物理力學參數見表2。

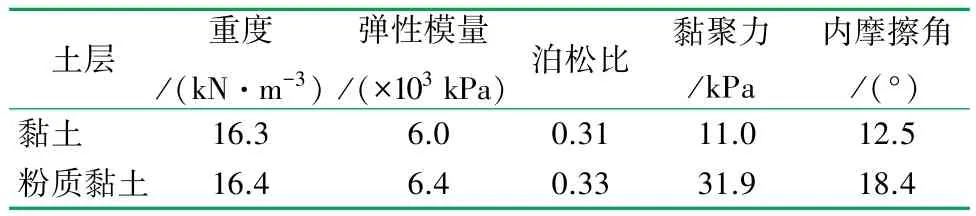
表2 土層物理力學參數表

1.3 模型建立過程

模擬列車荷載時，模型列車為B型車，采用4動2拖6輛編組形式，軸重為13 t，取單邊輪凈重65 kN，簧下質量區M0為750 kg。根據式(2)、(3)與表2，在i為1、2、3的控制條件下，對應的Li分別取 10、2、0.5 mm；αi分別取 5、0.4、0.08 mm；k1、k2分別取 1.6、0.8；v取 16.7 m/s。

不考慮隧道襯砌管片的拼裝方式對結構的影響，假定隧道一次建成且襯砌材料均勻。Plaxis3D程序根據所定義的邊界條件自動劃分單元并生成網格，隧道管片及隧道下方土體的網格加密。

施工步驟分為3個階段。初始階段選擇初始應力為“K0過程”，Plaxis3D將根據土體自身的平衡生成豎向應力，第1階段計算完成后，土體自重全部被激活，在其他計算階段中不可更改土的重度；第2階段為盾構隧道施工階段，凍結隧道土體，激活隧道襯砌結構及正向界面，將隧道結構材料定義為襯砌，激活建筑物面荷載；第3階段為動荷載作用階段，將式(4)所得數據整理為動力時間與荷載乘子相對應的形式，在荷載乘子選項卡中將其指定為動力乘子，激活動荷載。此外，為了模擬實際土體的半無限介質特性，邊界上設置黏性邊界，減少波在模型邊界上的反射干擾。

2 地鐵車輛運行對周圍土體影響分析

2.1 土體位移分析

不考慮臨近建筑物荷載的影響，列車荷載的加載時間分別取1、2、3 s，隧道下方土體測點的豎向位移變化圖如圖2所示。

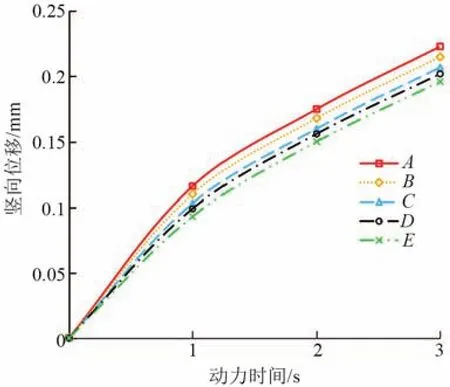
圖2 隧道下方測點豎向位移變化圖

隧道結構受列車振動荷載作用后，下方土體豎向位移值隨時間的增加而逐漸增大，但增加速率逐漸減小。豎向位移最大值出現在距隧道最近的A點處，下方其余各測點豎向位移值隨深度的增加而減小。循環荷載作用下土體的沉降變形可以分為兩部分，即循環荷載作用下土體的累計塑性變形引起的沉降，以及由于循環荷載造成的孔壓消散造成的固結沉降。在距離隧道較近的5 m深度范圍內，這兩種變形不斷衰減，且衰減速率較小。

2.2 土體加速度響應分析

地鐵列車動荷載作用于隧道結構時，土體應力應變場在加載初期發生較大的變化，產生較大的加速度響應值，數值模擬結果如圖3所示。加速度響應值在加載1 s時最大，而后隨時間逐漸減小，加速度響應值的衰減速率會隨著時間的增加而減小，且距隧道越近，該現象越明顯。從動力影響范圍分析，與土體豎向位移數據類似，土中加速度響應峰值同樣出現在A點處，隨著深度的增加而減小。加速度響應值由A點處的 0.006g減小至E點處的0.0007g，加速度響應峰值減少了88.3%。由此判斷在該工況下地鐵列車動荷載的影響深度主要為隧道下方5 m內。

圖3 隧道下方測點加速度響應變化圖

3 地鐵車輛運行對建筑物影響分析

3.1 地表測點沉降分析

建筑物尺寸為36 m×12 m，與隧道水平距離為12 m，建筑物荷載取90 kPa，施加列車振動荷載后地表觀測點S1、S2、S3的沉降與加速度響應變化如圖4所示。

在隧道運營階段，列車振動荷載的持續施加，使臨近建筑物產生一定量的沉降，如圖4(a)所示。列車振動荷載改變了隧道周圍土體的應力應變場，輻射至建筑物下方范圍，使基礎附加應力產生變化，土體產生沉降。建筑物與隧道間水平距離為8 m時，地表各測點豎向位移呈線性衰減。該現象與文獻[2]提出的在地表一定距離處出現局部放大現象相似。在這個局部放大區域內，地表沉降呈線性衰減趨勢。

與隧道下方土體加速度響應值相比，地表加速度響應值較小，隨水平距離的增加而衰減，如圖4(b)所示。由于地表土體在距離隧道約 0.5～1.5倍隧道直徑處出現局部放大效應，使得建筑物與隧道近端的土體加速度響應值衰減速率較小。水平間距為8～14 m的范圍內，加速度響應值僅減小27%；而水平間距在14～20 m的范圍內，加速度響應值減小了65%。說明地鐵列車振動荷載的主要水平影響范圍是在其產生局部放大效應的區域內。文獻[5]對局部放大現象的成因進行了分析，地表體波和瑞利波衰減速度不同而引起的振動疊加效應是造成上述現象的主要原因，單一頻率的地表振動響應將在距振源與埋深大致相當的近場處產生一個明顯的波峰或波谷，因此在距隧道0.5d至1.5d區域內出現局部放大現象。

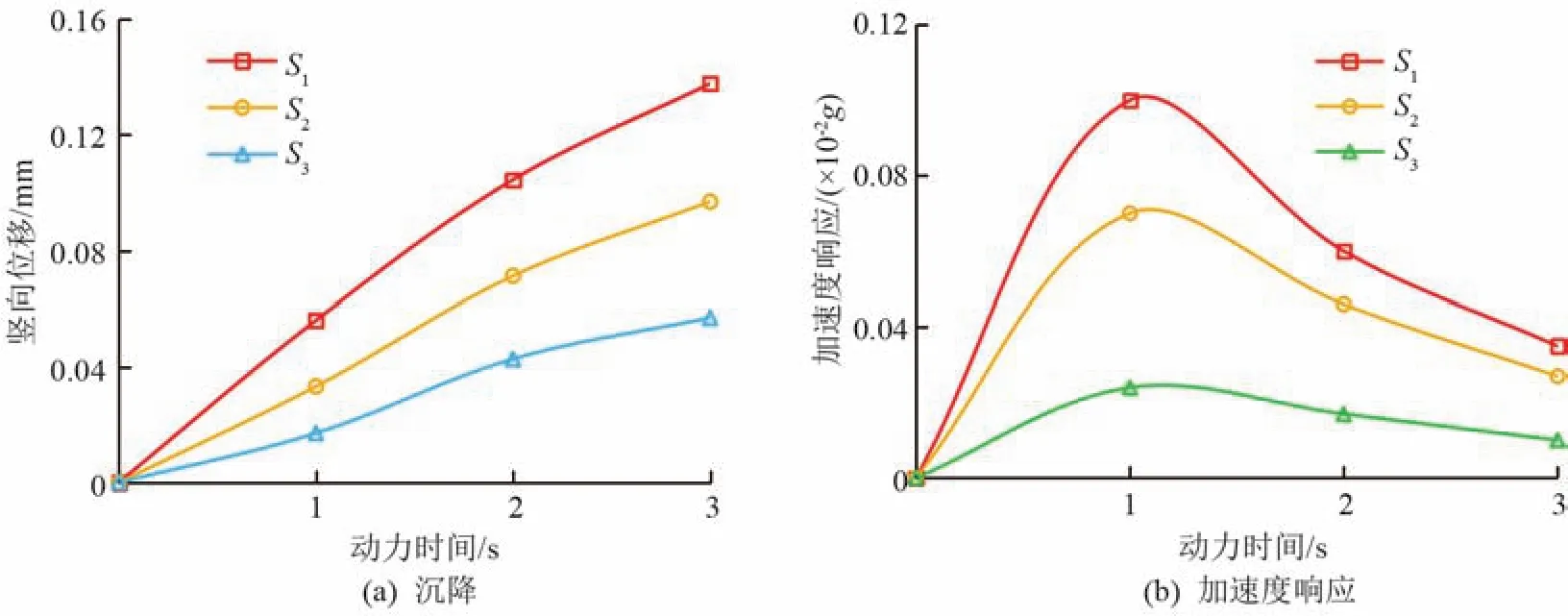
圖4 地表測點沉降與加速度響應變化圖

3.2 建筑物與隧道間水平距離的影響分析

改變隧道與建筑物的水平距離，對建筑物與隧道間水平距離l1為0、16 m，即0、2倍隧道直徑的建筑物進行模擬分析，建筑物荷載取90 kPa，沉降值如圖5所示。

建筑物與隧道間的水平距離對建筑物沉降的影響較為明顯。將圖5所示的改變水平距離后的建筑物沉降曲線與圖4(a)對比，地表存在建筑物時，距隧道0.5d至1.5d處的地表土體沉降值呈較為緩慢的線性衰減，在該區域的土體加速度響應值比較接近。同一加載時間下，水平距離為0 m時，最大沉降差為沉降量峰值的40.3%；水平距離為16 m時，最大沉降差則增加到沉降量峰值的79.5%。

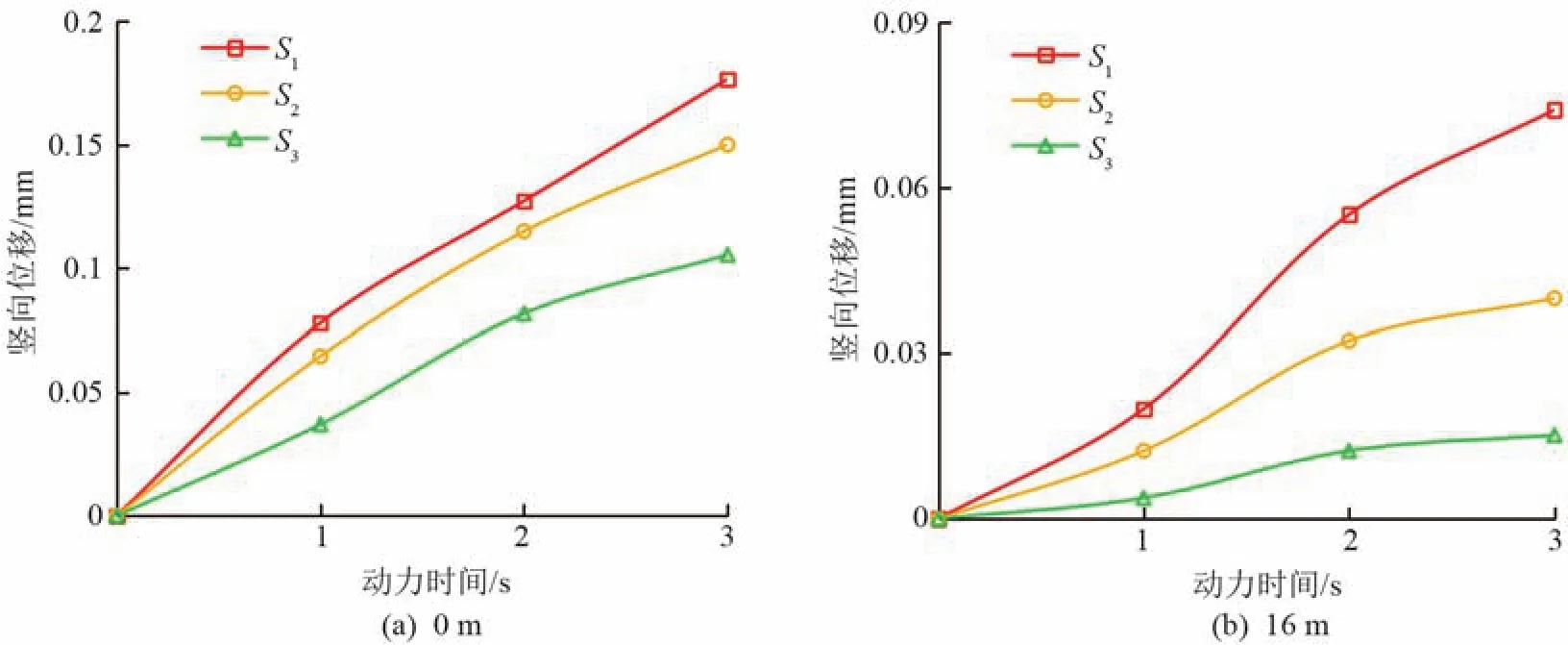
圖5 不同水平距離下地表測點沉降變化圖

最大沉降差隨水平距離的改變而產生較大變化的原因是，當隧道與建筑物間的水平距離為16 m時，建筑物有部分位于局部放大區域內，造成其遠點與近點沉降差值較大。同樣的，當隧道與建筑物間的水平距離＜4 m時，由于隧道上方的土體沉降衰減速率較小，而離開4 m的范圍后，沉降的衰減幅度又相對增大，導致建筑物的遠點與近點產生較大的沉降差。

3.3 隧道埋深的影響分析

隧道埋深的變化對振動荷載的影響范圍產生影響，改變隧道埋深，分別模擬隧道中心點埋深為-7、-9、-11、-13、-15 m 等5種工況。不同埋深下的測點S1處沉降及加速度響應值隨時間的變化曲線如圖6所示。

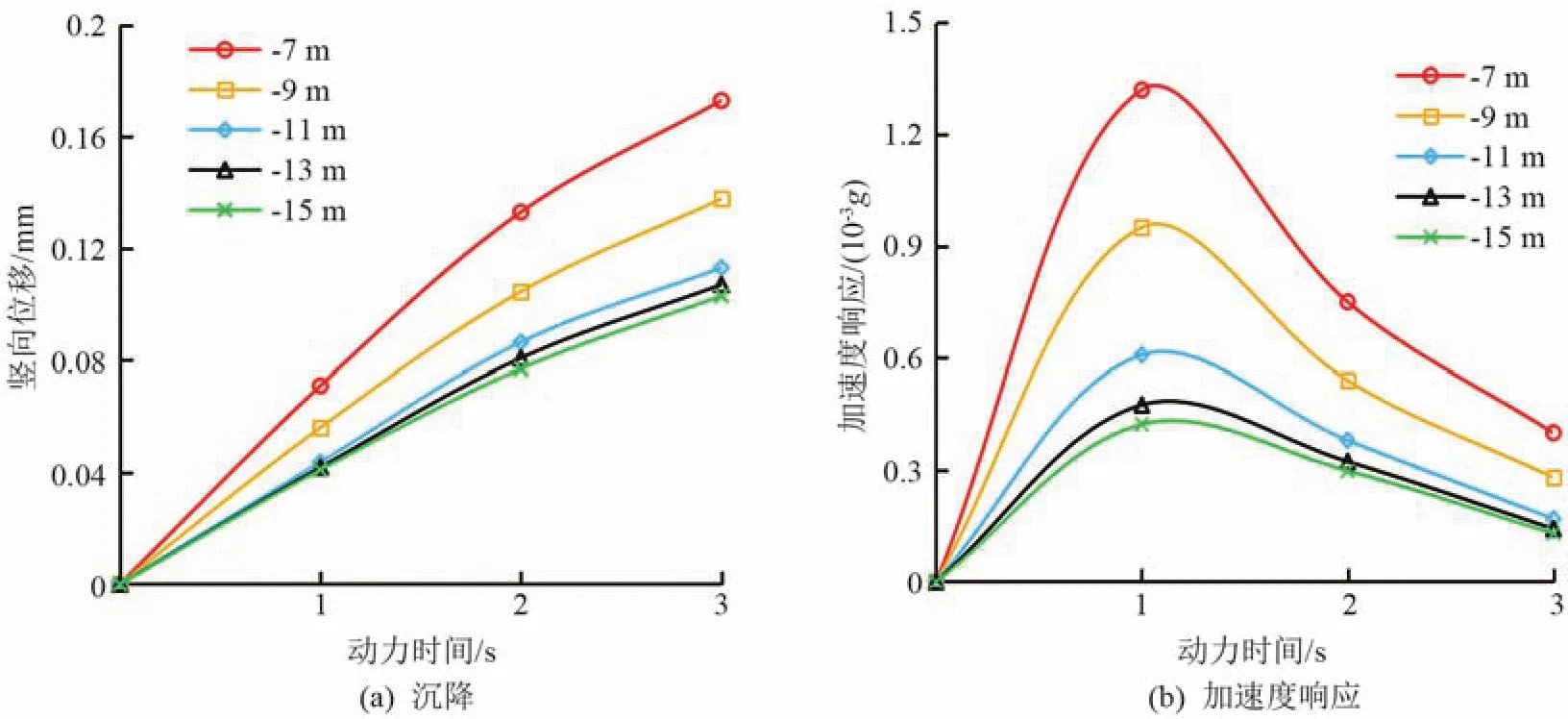
圖6 不同埋深下地表測點S1處沉降及加速度響應變化圖

如圖6(a)所示，隨著隧道埋深的增加，地表沉降值不斷減小。當隧道中心點埋深位于-7～-11 m范圍內時，在-9、-11 m位置處的最大沉降值分別減小18.35%、17.93%，而當隧道中心點埋深位于-11～-15 m的范圍內時，在-13、-15 m位置處的最大沉降值分別減小3.36%、2.78%，而在-11 m前后出現較大幅度的變化。同樣的，如圖6(b)所示，當隧道中心點埋深位于-7～-11 m范圍內時，在-9、-11 m位置處的加速度響應值分別減小36%、33.14%，而當隧道中心點埋深位于-11～-15 m的范圍內時，在-13、-15 m處的加速度響應值分別減小11.37%、8.26%，在-11 m前后出現較大幅度的變化。在上述的模擬工況中，隧道中心點埋深＞-11 m時，地鐵列車振動荷載產生的動應力應變場對地表土體的沉降影響較大；當隧道中心點埋深＜-11 m時，地表沉降量的衰減速率較小，最終的沉降量差值亦較小。

3.4 建筑物荷載對沉降的影響分析

建筑物荷載值的變化對地表沉降產生影響，改變其荷載值，分別模擬建筑物荷載為 0、30、60、90 kPa等4種工況。不同建筑物荷載下，地表S1測點的沉降變化如圖7所示。

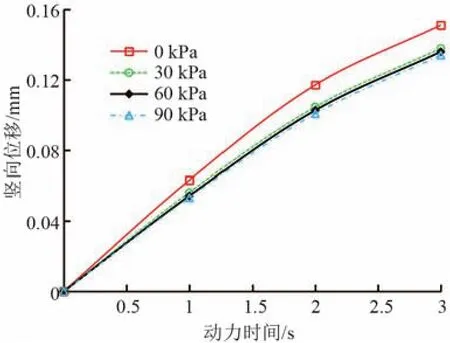
圖7 不同建筑物荷載下地表測點沉降變化圖

建筑物荷載對列車振動荷載所造成的地表沉降具有一定的約束作用。當建筑物荷載從0 kPa變為30 kPa時，地表測點S1處的最終沉降值減小了9.3%。而隨建筑物荷載值的增加，60、90 kPa的建筑物荷載所對應的沉降值分別減小1.37%、1.41%，約束效果并無明顯的增加，沉降量的變化率也較小。可見，隨建筑物荷載的增大，對地表沉降的約束效果變化較小。

4 結論

通過上述研究可知:

(1)隨著振動荷載加載時間的增加，隧道周圍土體的沉降值不斷增加，沉降的增加速率逐漸減小，振動荷載的主要影響區域位于隧道下方-5 m深度的土體內。

(2)地表沉降值隨著建筑物與隧道水平距離的增加而減小，在局部放大區域內，振動荷載在地表產生的加速度響應值衰減速率較小，遠離該區域后，加速度響應值的衰減速率增大。

(3)地表沉降值與加速度響應值隨隧道埋深的增加而減小，二者的衰減速率在埋深-7～-11 m的區域內較大，在-11～-15 m區域內較小。在模擬的工況中振動荷載的影響深度＞-11 m。

(4)建筑物荷載對振動荷載所造成的地表沉降具有一定的約束作用，當建筑物荷載從0 kPa變為30 kPa時，地表沉降值減小了9.3%，但隨著建筑物荷載的增加，該約束效果幾乎不變。