基于孔隙尺度的多孔骨架對固液相變的影響

張艷勇陳寶明李佳陽張自仕

(山東建筑大學熱能工程學院，山東濟南250101)

0 引言

相變儲能材料具有受熱、冷卻時發生固態—液態—固態周期性存儲和釋放能量的特性，已經應用到電池熱管理、太陽能發電等眾多領域。然而大多數的相變材料由于導熱系數及比熱容較小等原因，很大程度上影響了其在蓄熱和放熱過程的速度，因此提高相變蓄能材料的導熱系數具有重要的意義。在相變蓄能材料中加入高導熱性能的骨架材料，為解決相變材料這一不足提供了有效途徑[1]。

近些年，基于孔隙尺度的微觀研究由于可以得到多孔介質內部骨架和孔隙之間的詳細信息，克服在表征體元 REV(Representative Elementary Volume)尺度下多孔介質內部骨架和孔隙結構之間流動和傳熱方面的不足，而開始受到廣泛關注。Wang等[2]基于孔隙尺度，采用數值方法構建了6個四面體和2個不規則十二面體組成的W-P模型，模擬了開孔泡沫金屬在恒溫條件下的熔化傳熱過程，使泡沫金屬的孔隙率、導熱系數和相變材料的導熱系數對復合相變材料的有效導熱系數有顯著影響，但孔徑對其影響不大。成驥[3]對單質石蠟相變材料和泡沫鋁/石蠟復合相變材料的蓄熱性能進行了實驗研究，并對比了不同工況下的相變響應時間、溫度分布和蓄熱時間，相較于單質石蠟，復合相變材料的相變響應時間更短，溫度分布也更為均勻。此外，在7 000、12 000和15 000 W/m2等3種加熱工況下，復合相變材料的蓄熱時間比單質石蠟分別縮短了35.35%、22.14%、39.90%。 Abishek等[4]通過研究微觀形態對金屬泡沫石蠟復合材料的影響，發現高孔隙率泡沫金屬復合材料有利于提高和控制相變材料的融化速度，可用于熱能儲存或過程溫度控制。王慧儒等[5]采用高清相機和紅外熱像技術，對組合相變材料融化—凝固循環過程與傳熱特性開展了可視化實驗研究，組合相變材料的應用改善了蓄熱腔體各單元相變速率的均勻性，提高了平均相變速率。Jin等[6]采用高速紅外熱成像技術觀測到了熔融過程中典型時刻孔隙間溫度場的瞬態演變，得到小孔徑的泡沫銅能更好地加速相變材料的融化。杲東彥等[7]和陳振乾等[8]研究了泡沫金屬中相變材料的相變熔化過程，在相變材料中填充泡沫金屬，能有效改善相變材料的溫度分布；泡沫金屬孔隙率越小，石蠟熔化越快。杲東彥等[9-10]基于孔隙尺度分析了無量綱Ra數、孔隙率及孔密度等參數對融化相變傳熱過程的影響，發現相變材料的融化率隨著Ra數的增大、泡沫金屬孔隙率的減少及其孔密度的增大而增大。宋林泉等[11]基于孔隙尺度采用四參數法生成了多孔介質骨架，研究了其物性參數對固液相變過程以及糊狀區的影響。姚元鵬等[12]通過構建泡沫金屬內固液相變傳熱模型，對方腔蓄熱單元中泡沫銅強化石蠟相變蓄熱特性進行了數值分析，泡沫銅可以顯著改善石蠟相變的空間均勻性，減小了蓄熱區溫度梯度，使蓄熱速率和火用效率得到了有效提高。

由于多孔介質內部結構的復雜性以及固液相變過程中糊狀區內流動和換熱高度非線性的特點，傳統的數值計算方法在計算有關多孔介質內相變傳熱時往往會遇到邊界復雜、并行計算效率低的問題，而格子玻爾茲曼方法正好解決了傳統數值模擬在處理多孔介質內固液相變中遇到的問題。He等[13]對格子玻爾茲曼方法在多孔介質中單相和固液相變傳熱研究中的應用進行了詳盡的綜述，認為格子玻爾茲曼方法將在多孔介質固液相變傳熱的研究中發揮越來越重要的作用。對于純液相材料的固液相變過程，大量研究已經表明，固液共存的糊狀區對相變融化傳熱有很大的影響[14-15]，但固體骨架的存在對含固液相變過程糊狀區的演化和發展缺乏進一步的研究。文章采用描述糊狀區流動特征的多孔介質—多相流復合模型[16-17]，重點分析了無量綱瑞利數(Ra數)、普朗特數(Pr數)、斯蒂芬數(Ste數)對多孔介質內相變材料融化過程以及流動換熱的變化規律。

1 物理模型和數學模型的建立

1.1 物理模型的建立

物理模型如圖1所示，方腔尺寸高×寬=H×H，腔體內部隨機分布著四參數法生成的骨架，孔隙率為0.9，圖中白色部分表示固體骨架，藍色部分表示相變材料。相變材料的相變中心無量綱溫度為0.2，相變無量綱溫度半徑為0.1，多孔介質骨架方腔上下壁面絕熱，左壁面為高溫壁面，其無量綱溫度Th為1；右壁面為低溫壁面，其無量綱溫度Tc為0，而初始無量綱溫度T0為0。

圖1 方腔內多孔介質骨架模型示意圖

1.2 數學模型的建立

1.2.1 控制方程

基于兩區域模型，對糊狀區中高含液率區(r＞rtr)看作固—液兩相流，并將固—液兩相流看為不同組分混合的單相物質，將原來適用純流體的宏觀輸運方程直接用于固—液兩相流區域，而涉及的相關物性參數采用表征參數。低含液率區域(r＜rtr)采用適用范圍更廣的Brinkmann-Forchheimer-Darcy多孔介質滲流模型，其中滲透率、形態系數由液相率得到，從而建立更加準確的數學模型，在模型中高、低含液率的分界點rtr=0.7[16]。

數學模型中進行了簡化假設:(1)流體不可壓縮；(2)方腔內液相相變材料的流動為層流；(3)多孔基質和固體相變材料是剛性的；(4)固體和液相中的密度變化通過Boussinesq項進行近似；(5)相變過程中相變材料的體積變化忽略不計。

孔隙尺度下含糊狀區的固液相變的控制方程由式(1)～(3)表示為

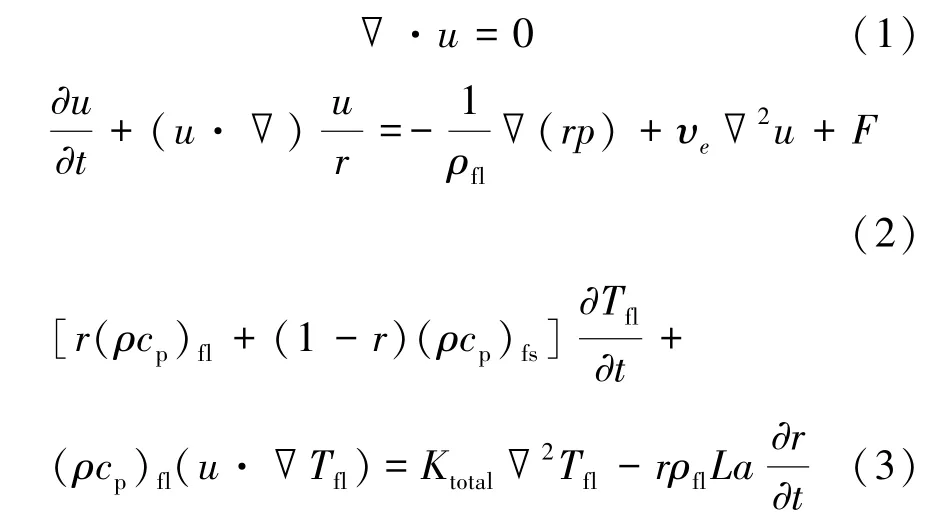
式中:u為滲流速度，m/s；t為時間，s；r為液相率(對應于多孔介質孔隙率)，其中r=0為固相區、r=1為液相區、0＜r＜1為糊狀區；下標fl和fs分別表示相變材料液相和固相；ρ為相變材料密度，kg/m3；cp為相變材料的熱熔，J/K；p為相對壓力，Pa；υe為有效運動黏性系數，m2/s；T為溫度，K；Ktotal為有效導熱系數，W/(m·K)；La為相變潛熱，J/g；F為外力源項，N。

固體骨架能量方程由式(4)表示為

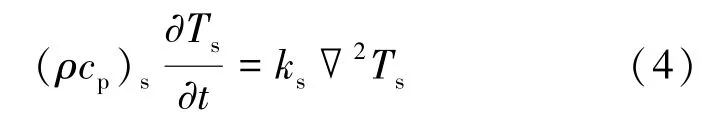
式中:下標s為多孔介質骨架；ks為骨架導熱系數，W/(m·K)。

F為外力源項，由式(5)表示為

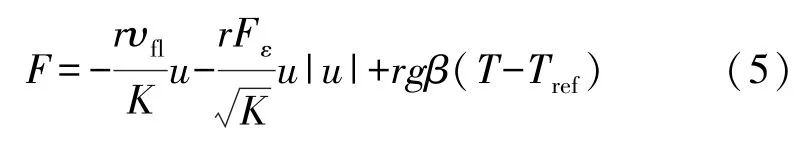
式中:υfl為液相流體的動力黏性系數，m2/s；K為多孔介質的滲透率，md；結構函數Fε為多孔介質的形狀因子；g為重力加速度，m/s2；β為熱膨脹系數，1/K；Tref為參考溫度，K。

在糊狀區的低含液率區域(r＜rtr)，對應的滲透率K、有效導熱系數ktotal分別由式(6)和(7)表示為

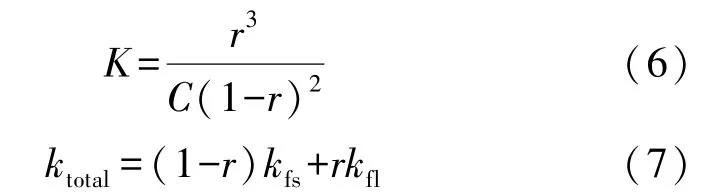
式中:C為糊狀區常數；在純流體區，r=1，式(1)～(3)轉化為純相變材料固液相變的控制方程；在固相區，r=0，式(1)～(3)轉化為導熱的控制方程；在糊狀區的低液相率區域，0＜r＜rtr，可看作多孔介質區域，該區域內流動、傳熱滿足式(1)～(3)；在高液相率區域，1＞r＞rtr，液固兩相流的表征導熱系數ktotal、表征運動黏度Ve由式(8)和(9)[18]表示為

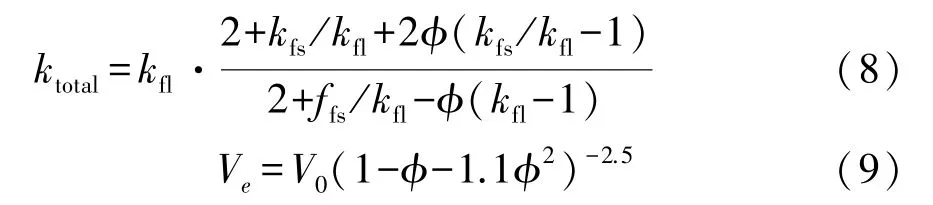
式中:?為相變材料固相體積分數，即?=1-r。

相變材料的液相分數由焓法求解，由式(10)[19]表示為

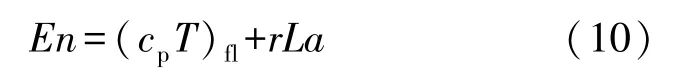
相變材料的焓值En和溫度Tfl之間的關系由式(11)表示為

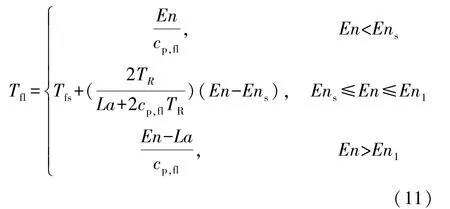
式中:Ens和Enl分別為相變開始時相應溫度Tfs的焓值和相變完成時對應溫度Tfl相應的焓值，J/kg；TR為相變半徑，TR=(Tfl-Tfs)/2，K。

根據相變材料的液相率，r由式(12)表示為

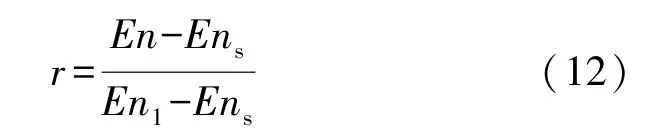
由式(10)～(12)可知，固體骨架傳熱的純導熱方程(4)中的溫度場與液相分數是相互耦合的，可以通過數值迭代求解。為減少控制方程中的變量，探討相變過程中糊狀區對相變過程影響的機理，引入的無量綱參數如

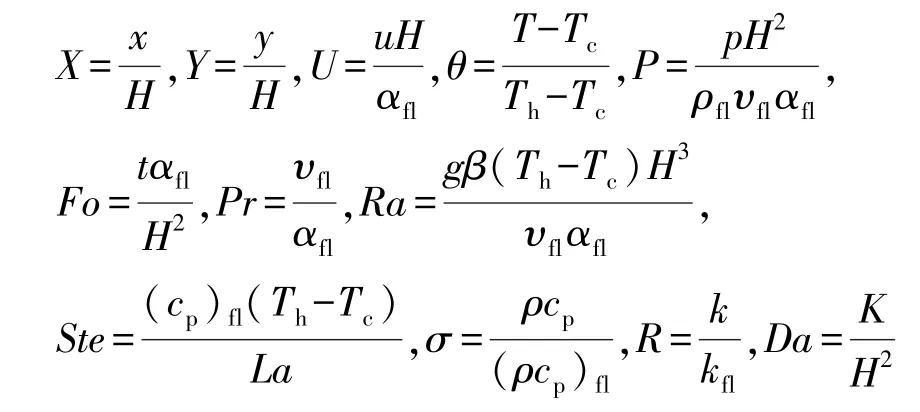
其中，αfl為相變材料的熱擴散率，m2/s；σ為有效熱熔比；R為有效導熱系數比；Da為達西數。把上述無量綱參數帶入到式(1)～(4)中，得到對應的無量綱控制方程分別由式(13)～(16)表示為

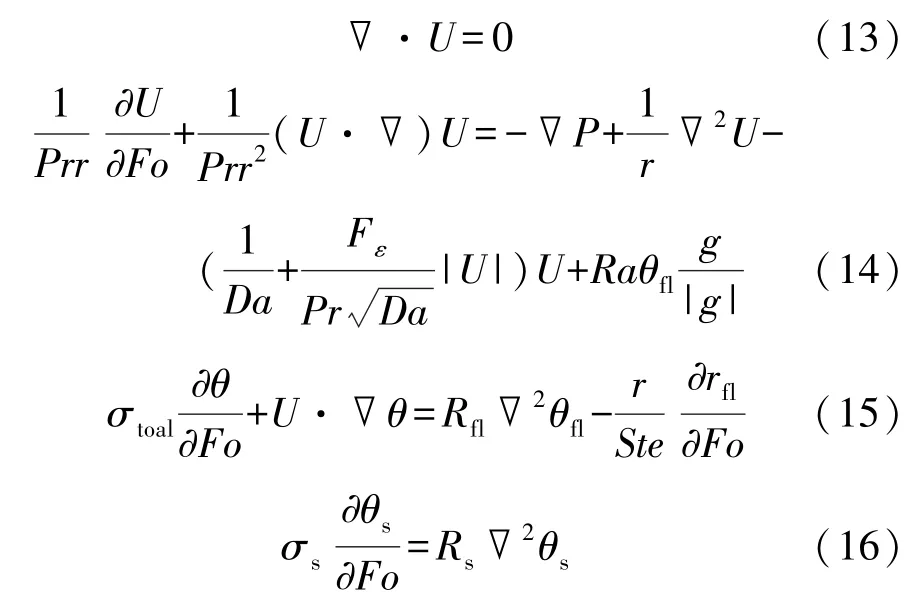
式中:σtotal為有效熱熔比；Rs為有效導熱系數比。

1.2.2 相變格子玻爾茲曼

求解用雙分布格子玻爾茲曼方法 D2Q9模型，模型對應的速度和溫度演化方程及平衡態方程由式(17)～(20)[20]表示為

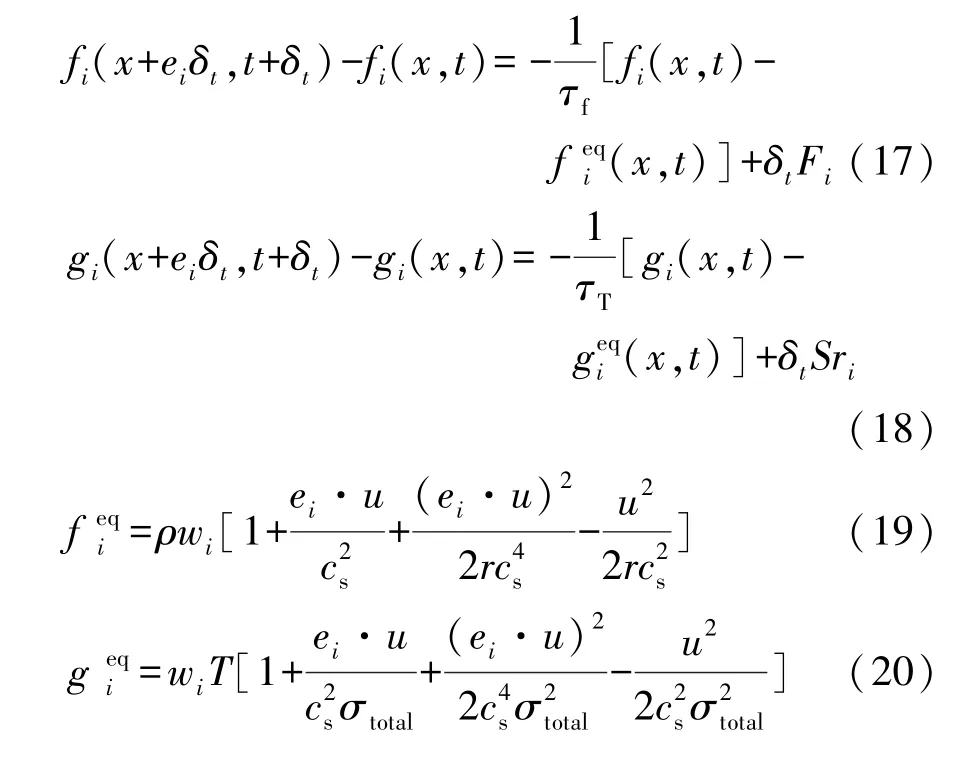
式中:fi(x，t)、gi(x，t)為t時刻x位置的微粒在i方向上的分布函數，簡寫成fi、gi；δt為格子時間步長；wi為權系數；ei為i方向上的格子速度；cs為格子聲速。

對應源項Fi、Sri分別由式(21)和(22)表示為

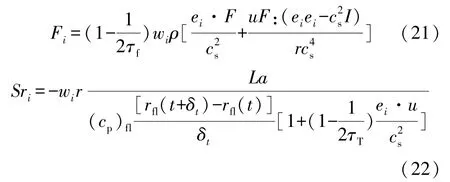
速度與溫度演化方程中的無量綱松弛因子τf、τT分別由式(23)和(24)表示為

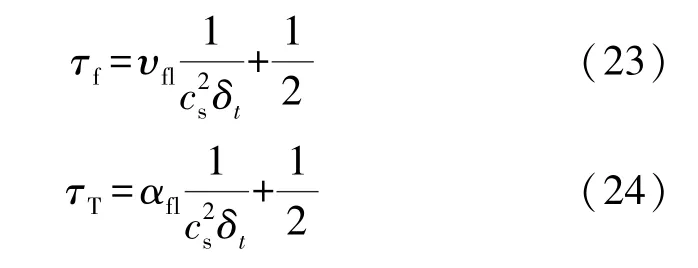
宏觀密度、速度和溫度由式(19)和(20)求得，由式(25)～(27)表示為

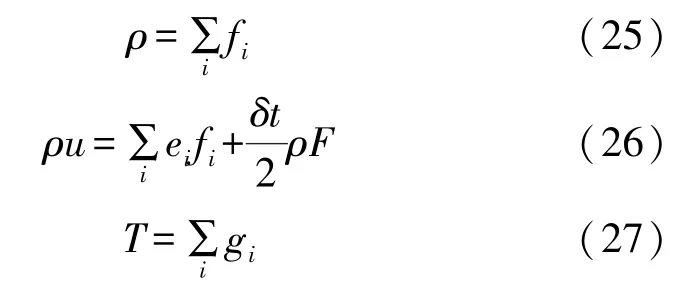
外力源項F中含有流動速度u，通過求解，由式(28)表示為

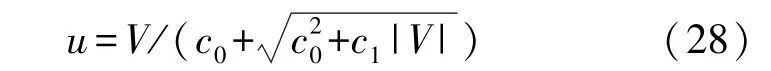
式中:V為臨時速度，由式(29)表示為

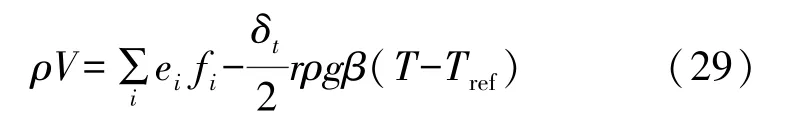
式中:c0、c1分別由式(30)和(31)表示為

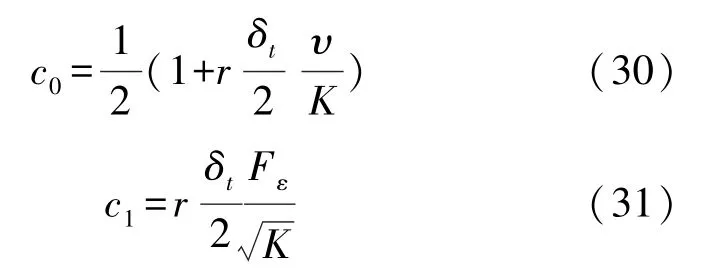
使用多尺度Chapman-Enskog方法對演化方程式(17)和(18)展開，可得到對應的宏觀方程式(1)～(4)。

2 網格無關化的驗證

4種不同網格數，無量綱參數Ra為5.0×105、Pr為1、Ste為5時，高溫壁面平均Nu數隨無量綱時間Fo數的變化曲線圖如圖2所示。無量綱Nu數定義由式(32)表示為

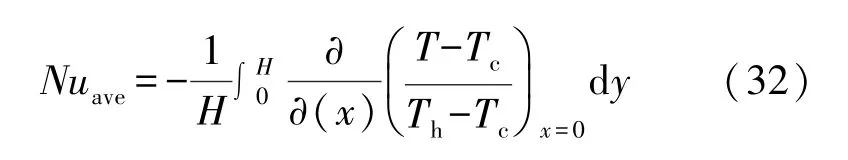
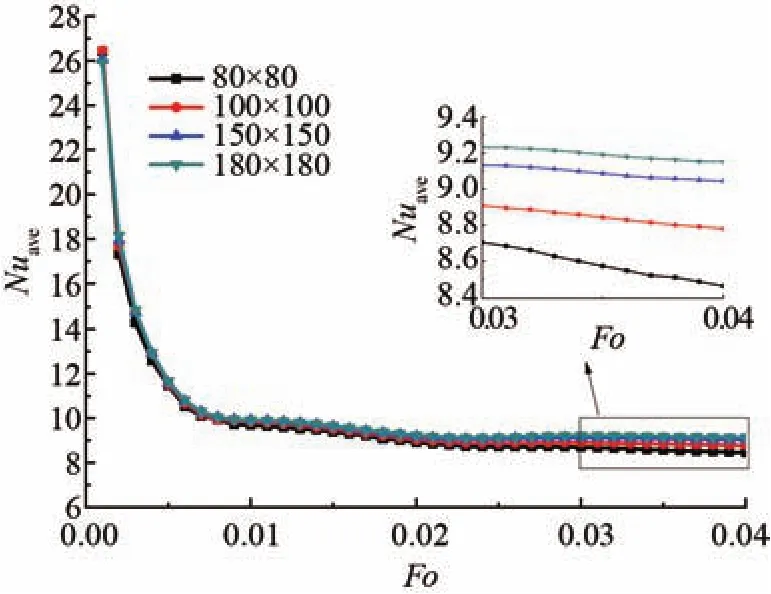
圖2 4種網格數下高溫壁面平均Nu數隨無量綱時間Fo的變化圖

以最大網格數180×180為基準，比較其他3種網格數下高溫壁面平均Nu數的相對誤差，網格數分別為80×80、100×100、150×150 時，其相對誤差分別為4.328%、3.258%、1.904%。可以看出，隨著網格數的增加，相對誤差越來越小，當網格數為150×150時，其相對180×180網格數的相對誤差僅為1.904%，因此可以認為網格數為150×150時滿足精度要求。

3 結果與分析

3.1 Ra數對融化換熱的影響

當Ste為 10、Pr為 1，而Ra分別為 104、105、106情況下，固液相變過程中不同時刻的液相率場、流場的分布情況如圖3所示。白色代表固體骨架，紅色代表液相相變材料，藍色代表固相相變材料，介于紅藍之間的為糊狀區。由圖3可知，當Ra數相同時，在相變發生的初期，糊狀區基本與上下壁面垂直，因為熱量的傳遞方式主要是導熱，隨著融化的進行，在自然對流浮升力的作用下，流體先流經方腔上部，然后再流到方腔下部，導致方腔上方得到的熱量多于下部，因此產生了糊狀區彎曲，且呈現上窄下寬的形狀。同時可以看到糊狀區邊界的不平滑，這主要是由于骨架的不規則性引起的。但當Ra數較小時，糊狀區從開始時刻至達到準穩態階段一直與上下壁面垂直。當Ra數不同時，相同Fo數下Ra數越大，相變材料融化速率越快，且糊狀區上窄下寬現象越明顯。由分析可知Ra數對多孔介質內固液相變過程有很大的影響。

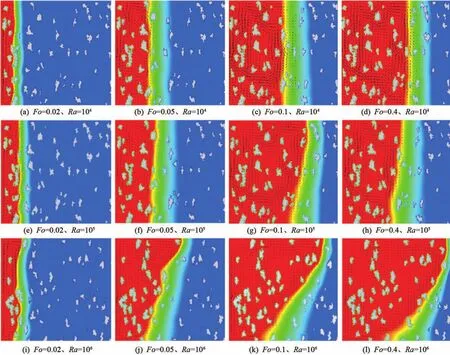
圖3 不同Ra下相場隨Fo數變化云圖

在不同Ra數下液相率和熱壁面平均Nu數隨Fo數變化圖如圖4所示。融化率隨著Fo數的增加而增加，直至趨于穩定；熱壁面平均Nu數隨著Fo數的增加而急劇下降，并緩慢減少直到達到準穩態時趨于穩定。在Fo＜0.05時，相變發生的初期由于熱量傳遞主要通過熱傳導進行，故不同Ra數下的融化率和高溫壁面平均Nu數發生重合，此時Ra數對融化傳熱影響不大，且熱壁面處的溫度梯度逐漸減小，導致在初始時刻平均Nu數急劇下降。隨著時間的推移，當0.05＜Fo＜0.4時，由于自然對流強度的增強，液相區逐漸增多，融化率逐漸增大，換熱的主要方式由熱傳導逐漸轉變為自然對流換熱，限制了熱壁面平均Nu數的急劇下降，直到達到準穩態階段(Fo＞0.4)，高溫壁面處的Nu數和液相率都達到穩定。對比不同大小的Ra數，由于Ra數越大表示自然對流強度越強，故隨著時間的增加，Ra數越大，融化速度越快，且達到準穩態階段時，融化率和熱壁面Nu數都越大。

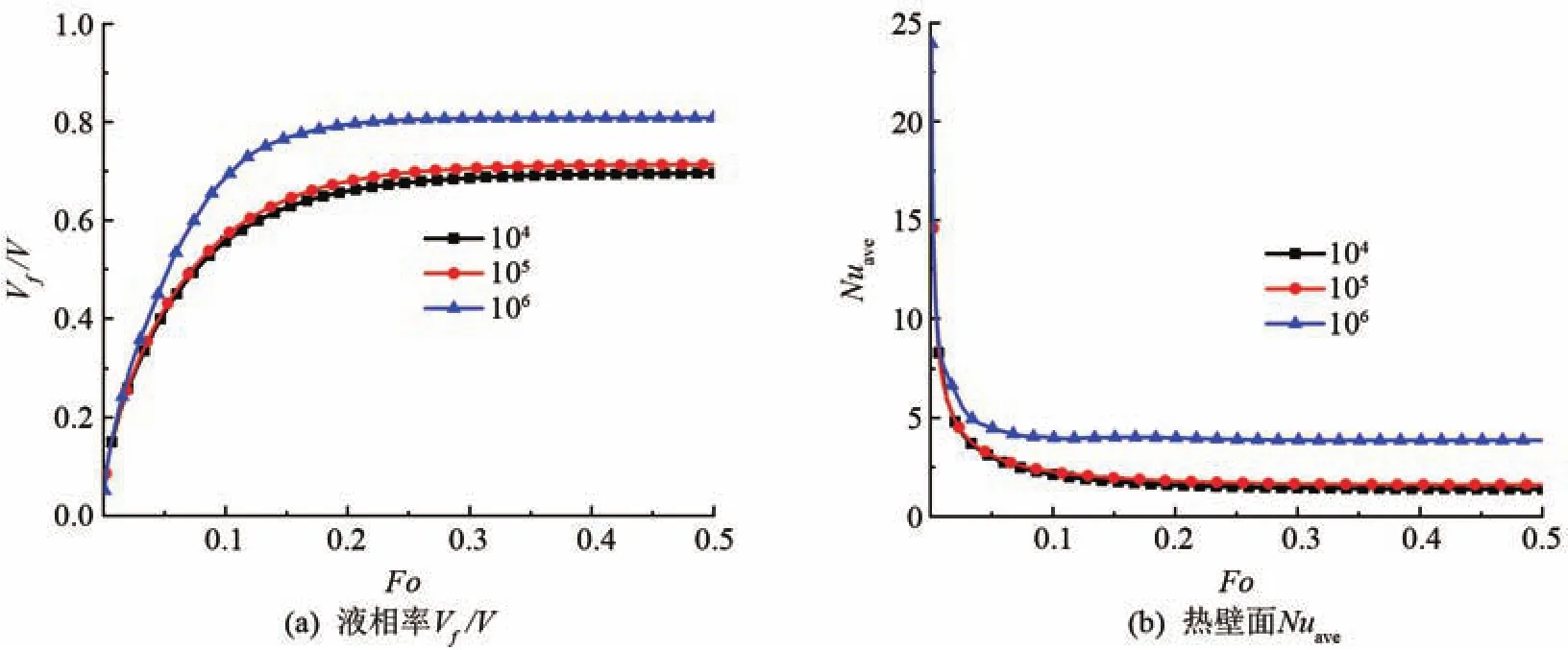
圖4 不同Ra數下液相率Vf/V和熱壁面Nuave隨Fo數的變化圖

3.2 Ste數對融化換熱的影響

Ste數表示相變顯熱與相變潛熱的比值。Ste數分別為0.1、1和10時，在Ra為106、Pr為1的情況下，相變材料的液相率隨無量綱時間Fo數變化如圖5(a)所示。Ste數越大，在同一時刻相變材料的液相率和融化速度都越大。主要是因為Ste數越大，相變材料融化顯熱越大，潛熱就越小，高溫壁面傳遞的熱量更多地用于相變材料的溫升，而不是作為潛熱儲存在相變材料中，從而更易達到相變所需要的溫度，導致方腔內的自然對流強度增加。

不同Ste數下熱壁面平均Nu數隨Fo數變化曲線如圖5(b)所示。在融化的前期，Fo＜0.02時，熱壁面平均Nu數迅速下降；0.02＜Fo＜0.4，Nu數下降緩慢；Fo＞0.4，熱壁面Nu數不再發生變化。主要是在前期熱量的傳遞以導熱為主，隨著時間的推移自然對流傳熱逐漸增加。對比3種情況下的Nu數變化曲線，Ste數越小，到達準穩態階段，熱壁面平均Nu數就越大。主要是因為Ste數越小，其潛熱越大，相變材料融化所需要的熱量就越多，左側熱壁面傳遞的熱量不易向低溫壁面傳遞，而是累積下來融化相變材料，故高溫壁面溫度梯度就會越大，從而熱壁面平均Nu數就越大。

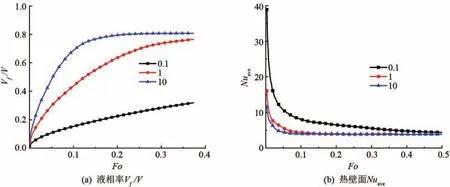
圖5 不同Ste數下液相率Vf/V和熱壁面Nuave隨Fo數的變化圖

3.3 Pr數對融化換熱的影響

在流體流動與傳熱的研究中，Pr數作為一個無量綱參數來表征流體的動量交換能力和換熱能力，反映了流體的物理性質對流體流動與傳熱過程的影響。為了研究Pr數對多孔介質骨架內固液相變的影響，分別取Pr為0.01、0.1和1，其他參數為Ra為106、Ste為10。液相率和熱壁面Nu數隨無量綱時間Fo數的變化如圖6所示。在Pr分別為0.1和1工況下，當Fo＞0.15時，相變材料的融化率曲線幾乎完全重合，在低Pr數下(Pr＜0.1)，隨著Pr數的增加，相變材料的融化速度越快，且達到準穩態階段時，融化率和熱壁面Nu越大。Pr數表征流體流動中動量擴散與熱量擴散之間的比值，Pr數越大，表征流體流動中動量擴散能力越強，自然對流越強，融化速率越快，達到穩定狀態時熱壁面平均Nu數越大。

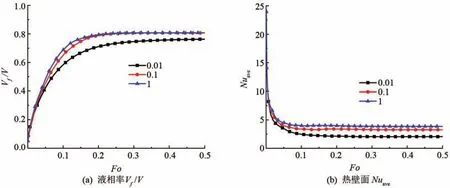
圖6 不同Pr數下液相率Vf/V和熱壁面Nuave隨Fo數的變化圖

4 結論

通過上述研究，得到以下結論:

(1)對于方腔內填充多孔介質骨架的固液相變過程，相變初期，糊狀區與上下壁面近似垂直，隨著相變的繼續進行，糊狀區緩慢向前推移，并開始發生彎曲。

(2)隨著Ra數的增加，自然對流作用增強，相變材料融化速度變大，達到準穩態階段時，融化率和熱壁面Nu數都增大。

(3)隨著Ste數的減小，多孔介質方腔內相變材料自然對流換熱能力減弱，在相同的時間下融化速率越慢，而Ste數越小，相同時間下熱壁面平均Nu數越大。

(4)隨著Pr數的增加，相變材料的融化率和高溫壁面Nu數都隨之增加，對于低Pr數(Pr＜0.1)，隨著Pr數的增加，達到準穩態時，熱壁面平均Nu數和最終的液相率都逐漸增加，且增加幅度較大。但當Pr數增加到一定程度時(Pr=0.1)，隨著Pr的增加，達到準穩態階段時相變材料融化率不再發生變化。