求解散射問題中消除多次透射邊界飄移失穩措施的效果分析

唐暉　李小軍

摘要：針對應用多次透射人工邊界公式求解散射問題時可能出現的飄移失穩現象，對比分析了實時降階法、修正算子法、附加黏彈器法和改進輸入法的消飄效果和對計算精度的影響，結果表明：4種方法均可有效消除或抑制比較緩慢的飄移失穩現象;飄移趨勢強烈時，修正算子法和附加黏彈器法可能無法有效地抑制失穩;當阻尼較小時，采用實時降階法可能引入額外的低頻誤差;在能夠確定適當參數值的前提下，修正算子法和附加黏彈器法能夠提高低頻計算精度;改進輸入法則無需人為設置參數，能夠在抑制飄移失穩的同時提高計算精度。

關鍵詞：多次透射人工邊界公式;飄移失穩;消飄措施

中圖分類號：P315.9?文獻標志碼：A?文章編號：1000-0666（2019）04-0493-10

0?引言

多次透射人工邊界（MTF）是由Liao和Wong（1984）提出的可具有N階精度的局部人工邊界條件，其基本思想是直接模擬外行波穿過邊界的過程，通過與邊界點相鄰的內部點在現在時刻以及前幾個時刻的運動給出邊界點在下一時刻的運動量。這種時空解耦的邊界條件不僅物理意義清晰，且易于在數值離散計算中實現，良好的普適性、靈活性以及計算效率等方面的明顯優勢使其能夠在求解復雜問題中發揮積極的作用，得到廣泛應用（楊光，劉增武，1994;李小軍等，1995;金星等，2004;丁海平等，2006;孔戈等，2007;徐建平等，2008;陳少林等，2010;盧再華等，2010;唐暉等，2012;李鐵飛等，2013;方宏遠，林皋，2013）。

與其它局部邊界相同，該邊界條件在應用中也存在穩定性問題，這也一直是人們關注的重要問題。為了消除或抑制多次透射人工邊界可能引入的飄移失穩，李小軍和廖振鵬（1996）首先針對散射問題探討了低頻飄移現象的形成機制，指出入射波場采用連續介質解析解與離散模型中實際入射波之間的差別會導致低頻飄移失穩，并給出了計算過程中實時降低透射階數以穩定計算的建議;周正華和廖振鵬（2001，2004）基于雙曲型偏微分方程數值解穩定性GKS準則給出飄移失穩的另一個解釋，即多次透射人工邊界無法阻止波動中的零頻成分進入計算區域，提出了在多次透射人工邊界公式中加入修正算子的消除漂移失穩措施;李小軍和楊宇（2012）嘗試在邊界施加黏彈性組件來抑制飄移失穩;唐暉等（2016）給出了一種改進的波動輸入方法，即通過劃分邊界區，計算獲得入射波場的數值解以實現波動輸入，從而減小入射波場采用解析解引入的誤差以消除或抑制低頻飄移現象。

實際工程中采用何種消除飄移失穩措施（后文簡稱消飄措施），除了考慮其能否在計算時間內消除或抑制飄移失穩現象，還須考量所采用方法對于計算精度的影響，尤其是對低頻響應較為敏感的長周期結構等。鑒于此，本文針對利用多次透射人工邊界求解如構筑物抗震分析等波動散射問題時可能出現的飄移失穩現象，綜合對比分析實時降階法、修正算子法、附加黏彈器法和改進輸入法在消除飄移失穩方面的效果和對計算結果精度的影響，以期為多次透射人工邊界條件在工程中應用提供有益的參考。

1?飄移失穩機制

對于采用多次透射人工邊界時出現的飄移失穩機制有2種：一種是從透射邊界公式本身出發，另一種是針對利用多次透射人工邊界求解散射問題的情況。

第一種（周正華，廖振鵬，2001，2004）定義傳遞因子為Bmn，傳遞函數為：

式中：upj代表計算區域內與邊界相距jcaΔt、處在時刻pΔt的位移，其中ca為人工波速，Δt為離散時間步距;j，p，m和n均為任意非負整數，將N階透射人工邊界公式表示為：

依據GKS準則，計算中不出現飄移失穩的充分條件為：任何滿足內域內行波的波動解，不同時滿足邊界條件。那么，對于滿足內域的彈性波動解為：

將式（3）代入式（2）可以得到多次透射邊界不飄移失穩的條件：

然而，對于零頻和零波數，即ω=k=0的波動成分時，式（4）不成立，即零頻成分可以從多次透射人工邊界條件進入計算內域，從而引起飄移失穩。謝志南（2014）利用模態分析法進一步分析了相應的飄移失穩機制，并在此基礎上結合Z變換解釋了零頻飄移失穩數值解的增長模式。

另一種，李小軍和廖振鵬（1996）指出在求解散射問題時，為了利用透射邊界模擬外行波，地震波動輸入過程中需要將總波場分離為入射波場和外行波場：

U=Ui+Us（5）

式中：U，Ui和Us分別代表總波場、入射波場和外行波場。然而，離散網格中實際入射波場不易獲得，往往采用解析解，其與真實入射波場之間存在一定差別，公式如下：

式中：Uci，Ucs和ΔU分別代表計算中的入射波場、外行波場以及計算入射波場和真實入射波場之間的誤差。將式（6）（7）代入式（5）可以得到：

即透射邊界模擬的外行波不僅包含真實的外行波Us，還包含了入射波場誤差ΔU，這會導致飄移失穩現象的產生。

2?消飄措施

2.1?實時降階法

李小軍和廖振鵬（1996）指出由于入射波場引入的誤差會導致飄移失穩趨勢的出現，并且證明了當外行波場出現式（9）和（10）的失穩趨勢時，利用二次及二次以上透射公式時，計算飄移失穩趨勢將會繼續，即高階透射公式將可能引起計算飄移失穩現象：

式中：upJ-i表示在時刻pΔt、計算區域內垂直于邊界并距離邊界節點J的第i個節點（i=0，1，…，m）的外行波位移。基于此，李小軍和廖振鵬（1996）給出了實時降低透射階數以消除飄移失穩的方法，在計算過程中對邊界點和對應的區域內m個節點進行實時監測，一旦滿足如式（9）和式（10）給出的條件，則之后的n個計算步均采用一階透射公式。

2.2?修正算子法

基于飄移失穩機制的第一種解釋，周正華等（2001，2004）針對邊界條件式（2）進行了修改：

式中：γ是任意小正數。

將式（3）代入式（11）得到對于任何頻率均可滿足的條件式：

2.3?附加黏彈器法

李小軍和楊宇（2012）嘗試在邊界區節點施加黏彈性元件，以約束邊界區域不合理位移，從而消除高頻或飄移失穩趨勢向計算內域的延續。該方法將邊界區內包括邊界點J在內的邊界法向上2N個節點（N階透射公式）的動力方程定義為：

式中：[M]為質量矩陣;[K′]和[C′]分別為對體系固有的剛度矩陣[K]和阻尼矩陣[C]進行修正后的阻尼矩陣和剛度矩陣：

式中：k0和c0為附加彈簧的剛度系數和附加阻尼器的阻尼系數。

2.4?改進波動輸入法

基于消除或減小所采用的入射波場與有限元網格中的實際入射波場的差別，從而消除或抑制飄移失穩現象的思路，唐暉等（2016）給出了改進波動輸入的方法，嘗試利用多次透射人工邊界條件獲得網格中實際入射波場用于波動輸入中。該方法無需根據試算或經驗設定參數，計算方便并能提高計算精度。

3?消除飄移措施分析

如上文所述，在應用多次透射公式求解實際工程問題，尤其是對低頻成分敏感的構筑物地震響應時，不僅要關注所采用的消飄措施能否有效消除或抑制失穩現象，還須關注其對計算精度的影響。因此，下文將對這2方面開展對比分析。需要特別說明的是，波動有限元中瑞利阻尼的質量系數使得零波數及鄰近波動對應為非行進波，但該數值對計算穩定性影響較小，而剛度系數使得行波的衰減隨波數增大而增大，能夠抑制高頻失穩（章旭斌，謝志南，2017），因此，下文分析中僅考慮瑞利阻尼的剛度系數。

3.1?消飄措施效果分析

3.1.1?算例一

如圖1所示的均勻水平地表場地，有限元模型尺寸為L=300?m、H=100?m，網格尺寸為2?m×2?m，S波波速為2?100?m/s，瑞利阻尼剛度系數β=0.001，如圖2所示的SH波位移脈沖以角度θ=45°入射，采用二階透射人工邊界。

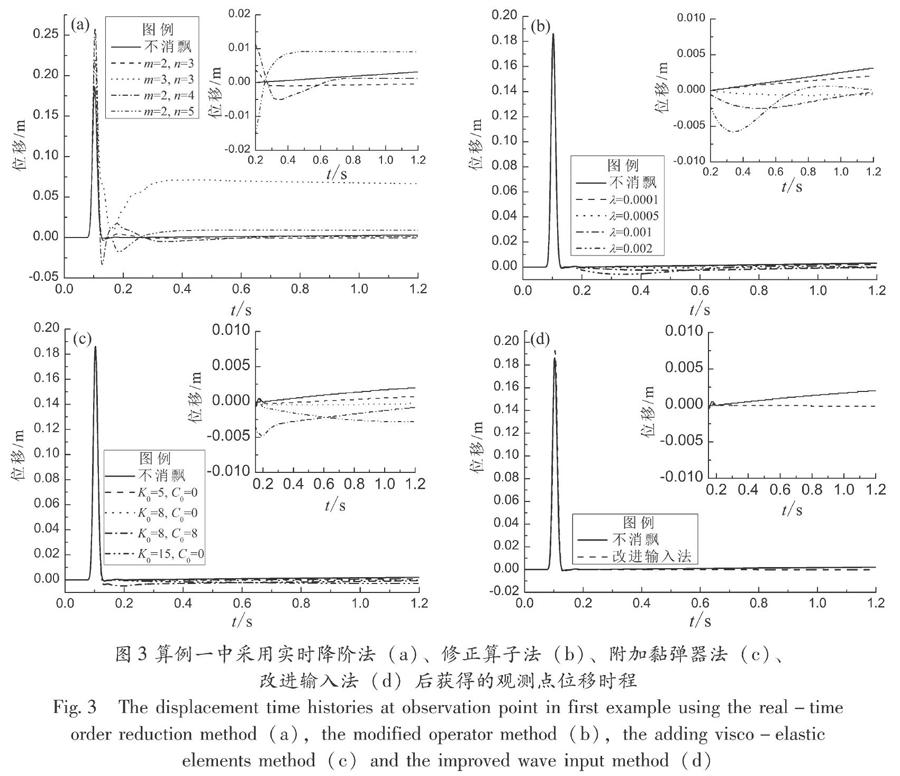
當采用實時降階法時，式（9）或（10）中用于判斷失穩趨勢的節點數和連續使用一階透射的時間步數，即參數（m，n）分別為（2，3）（3，3）（2，4）和（2，5），計算所得地表觀測點的位移時程如圖3a所示，本算例中飄移失穩趨勢較為緩慢。如何設置用于判斷失穩趨勢的節點數和連續使用一階透射的計算步數對于消飄效果會產生顯著影響，其中（m，n）為（2，3）的消飄效果較好，而一階透射計算步數增加為4和5時，計算誤差隨之增加，在計算時間內無法有效抑制低頻飄移，當m=3時，即基于邊界法向上包括邊界節點在內的4個節點判斷失穩時，計算結果會出現更明顯偏離。

圖3b為采用修正算子法獲得的計算結果，其中修正算子λ取值分別為0.000?1，0.000?5，0.001和0.002。當λ=0.000?1時，對計算結果影響有限，無法有效抑制飄移現象;λ=0.000?5時，該方法較好地消除了飄移失穩;而λ=0.001和0.002時，給計算結果引入了較大的低頻干擾。

采用附加黏彈器法在邊界設置附加彈簧和附加阻尼系數分別為（5，0）（8，0）（8，8）和（15，0）時，相應的計算結果如圖3c所示，其中附加彈簧和附加阻尼系數為（8，0）時能夠有效地消除飄移失穩，與修正算子法類似，其消飄效果依賴于附加彈簧系數和附加阻尼系數取值。

采用改進輸入法獲得的觀測點位移時程如圖3d所示，該方法可以有效地抑制低頻飄移現象，重要的是，采用該方法不需要依據經驗試算設定參數。

3.1.2?算例二

如圖4所示的不規則凹陷場地，計算區域尺寸為L=950?m，H=200?m，SH波以30°從左下角入射，其位移時程如圖2所示，S波波速2?100?m/s，瑞利阻尼與算例一相同，最小網格為2?m左右。采用實時降階法，修正算子法，附加黏彈器法和改進輸入法獲得的觀測點位移時程和其頻譜曲線如圖5所示。與算例一不同，該算例中飄移失穩趨勢較為強烈，當m=2以及連續使用一階透射的次數n為3，4和5時，實時降階法均能在計算時間內較好地抑制飄移失穩，而m=3時無法抑制或消除失穩現象。修正算子法中修正算子λ分別為0.000?1，0.001，0.002和0.005，修正算子λ越大，對飄移現象的抑制作用越強，但也會給計算結果帶來過大的低頻干擾，從而失去了應用意義。而邊界設置附加彈簧和附加阻尼系數分別為（5，0）（15，0）（30，0）和（30，30）時，與修正算子法相同，無論如何設置黏彈器參數也無法在不過度引入低頻誤差的前提條件下有效地抑制飄移失穩現象。采用改進輸入法后，計算時間內失穩趨勢同樣得到了很好的抑制。

綜上可知，就二階透射而言，對于失穩現象較為平緩的情況，上述4種方法均能消除或抑制飄移失穩。基于邊界內幾個點判斷失穩趨勢以及失穩趨勢出現后采用一階透射時間步數都會對實時降階法的消飄效果產生影響，二者取值過大可能會給結果引入過多誤差，影響消飄效果，建議判斷失穩趨勢時，式（9）（10）中m和連續使用一階透射次數n分別取值2和3。修正算子法中修正因子λ如何選取十分關鍵，其取值過小無法很好地抑制或消除飄移失穩，取值過大則會影響計算精度，尤其是對于低頻波動成分，修正算子λ如何取值既能消除失穩又不過多影響計算結果精度。目前除了經驗試算仍沒有很好的方法，然而，對于一些復雜工程問題往往無法通過經驗試算來判斷λ取值是否合理。與修正算子法類似，附加黏彈器法亦需要通過經驗試算確定。改進的輸入法可以有效地消除飄移失穩，并獲得合理的計算結果。

與實時降階法和改進輸入法不同，當失穩趨勢強烈時，修正算子法和附加黏彈器法可能無法在過多影響計算精度的前提條件下有效地抑制低頻飄移失穩。

3.2?消飄措施對計算精度影響分析

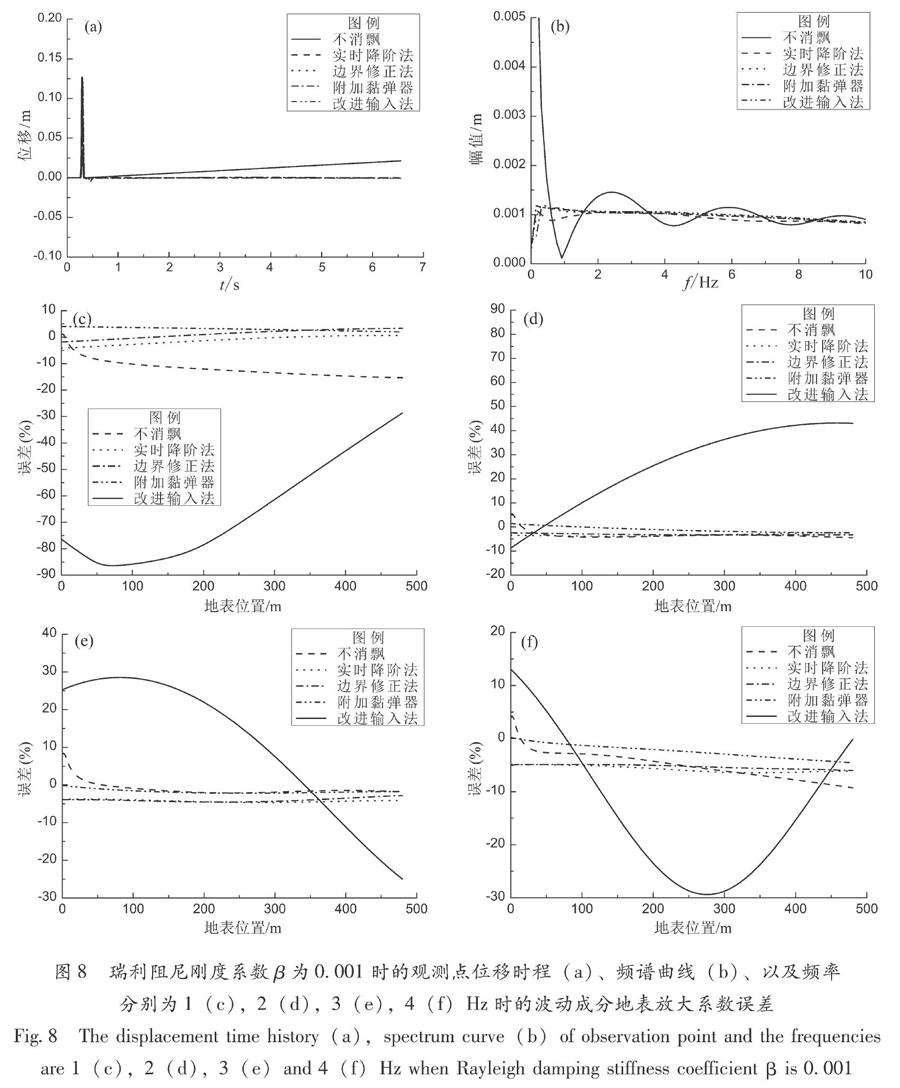
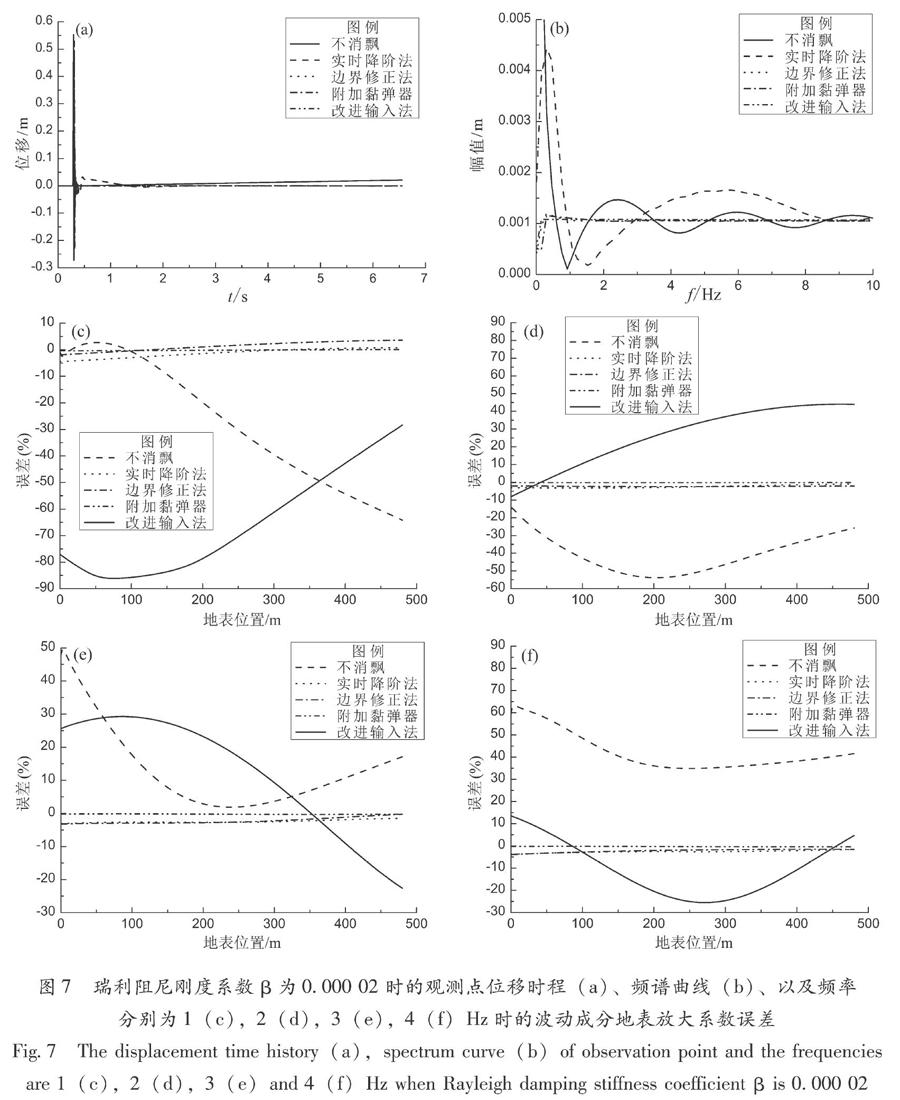
為了對比上述消除低頻飄移方法對計算精度的影響，以如圖1所示的水平均勻場地為算例，模型尺寸L和H分別為480和200?m，有限元網格亦為2?m×2?m，計算時間步距為0.000?2?s，位移時程如圖6所示，SH波從模型左下以45°角度入射。參考算例一的結果，實時降階法中用于判斷失穩的邊界內節點數和連續一階透射計算步數（m，n）為（2，3），修正邊界法中修正因子λ=0.000?5，附加黏彈器法中彈簧和阻尼系數為（8，0），在算例一中，4種消飄措施均能抑制飄移失穩現象。瑞利阻尼剛度系數為0.000?02和0.001時，地表觀測點的位移時程分別如圖7a和圖8a所示，其頻譜曲線分別如圖7b和圖8b所示，對于低頻波動成分為1，2，3，4?Hz，阻尼可忽略，地表處相對于輸入的放大系數可以近似為2，圖7c～f和圖8c～f則分別給出計算獲得的地表放大系數誤差。觀察輸入位移脈沖和計算所得地表觀測點的頻譜曲線、地表放大系數誤差曲線可以看出，當阻尼為0.000?02時，實時降階法雖然抑制了“零頻”飄移，卻給低頻成分的計算結果引入了更大的誤差，而阻尼為0.001時，該方法在抑制失穩的同時提高了低頻成分計算精度，這可能是因為低阻尼時高頻波動成分豐富，而實時降階法對這部分波動的計算精度影響較大，誤差波在計算區域疊加從而導致了低頻誤差增加。阻尼大小對其他3種消飄措施的影響較小，這3種方法不僅能夠在計算時間內消除“零頻”飄移現象，還能提高計算精度，其中，改進輸入法對低頻計算精度的提高最為明顯。

4?結論

本文對比分析了實時降階法、修正算子法、附加黏彈器法和改進輸入法等4種消飄措施的消飄效果和對計算精度的影響。得出以下結論：

（1）對于二階人工透射邊界，就消飄效果而言，當飄移失穩較為緩慢時，實時降階法、修正算子法、附加黏彈器法和改進輸入法均可用于抑制失穩，但是，前3種措施的消飄效果與其參數設置有關。當基于包括邊界點在內的3個節點的結果來判斷失穩趨勢，并在失穩趨勢出現后連續使用3

圖8?瑞利阻尼剛度系數β為0.001時的觀測點位移時程（a）、頻譜曲線（b）、以及頻率分別為1（c），2（d），3（e），4（f）Hz時的波動成分地表放大系數誤差次一階透射計算步數進行計算時，實時降階法的消飄效果相對較好。而為了消除失穩的同時不過多影響計算精度，修正算子法中修正算子以及附加黏彈器法中彈簧和剛度系數則需要通過經驗試算來確定。然而，對于許多復雜的實際工程往往無法評價參數的選取是否合理，改進輸入法不需要人為設置參數，且消飄效果良好。

（2）飄移失穩趨勢強烈時，修正算子法和附加黏彈器法可能會引入較大低頻誤差，從而失去了應用價值。不同于失穩趨勢緩慢的情況，實時降階法在基于包括邊界點在內的邊界內3節點判斷失穩趨勢，且連續使用一階透射次數大于或等于3次時，均能在計算時間內有效地抑制失穩現象。鑒于此，在利用實時降階法時，建議判斷失穩趨勢的節點選取包括邊界點在內的3個節點，且失穩趨勢出現后的3個計算步驟均使用一階透射;改進輸入法則仍能夠有效地抑制失穩現象。

（3）當4種措施都能抑制飄移失穩時，即計算出現緩慢的飄移現象時，實時降階法在阻尼較大時可以提高低頻成分計算精度，但是，由于降低透射階數也就降低了精度，所以，這方面不如另外3種措施，而阻尼較小時，該方法則可能會引起更大的低頻誤差。在能夠確定合適參數的前提條件下，修正算子法和附加黏彈器法可以在抑制低頻飄移的同時提高計算精度。改進輸入法不僅消飄效果良好，其對計算精度的提高也十分明顯，重要的是該方法不需要人為設置參數，應用較為方便。

對于三階及三階以上的高階透射邊界，單獨采用這4種方法均無法有效地消除或抑制失穩現象，而本文的研究結果提供了將改進輸入法和其他措施結合以消除失穩的思路。

參考文獻：

陳少林，唐敢，劉啟方，等.2010.三維土-結構動力相互作用的一種時域直接分析方法[J].地震工程與工程振動，30（2）：24-31.

丁海平，劉啟方，金星.2006.長周期地震動三維有限元數值模擬方法[J].地震工程與工程振動，26（5）：27-32.

方宏遠，林皋.2013.基于辛算法模擬探地雷達在復雜地電模型中的傳播[J].地球物理學報，56（2）：653-659.

金星，孔戈，丁海平.2004.水平成層場地地震反應非線性分析[J].地震工程與工程振動，24（3）：38-44.

孔戈，周健，徐建平，等.2007.盾構隧道橫向地震響應規律研究[J].巖石力學與工程學報，26（增刊1）：2872-2879.

李鐵飛，陳學良，高孟潭.2013.盆地場地效應的三維數值模擬研究進展及沉積環境對盆地場地的影響[J].世界地震工程，29（3）：56-68.

李小軍，廖振鵬，關慧敏.1995.粘彈性場地地形對地震動影響分析的顯式有限元-有限差分方法[J].地震學報，17（3）：232-244.

李小軍，廖振鵬.1996.時域局部透射邊界的計算飄移失穩[J].力學學報，28（5）：627-632.

李小軍，楊宇.2012.透射邊界穩定性控制措施探討[J].巖土工程學報，34（4）：641-645.

盧再華，張志宏，顧建農.2010.透射邊界在點聲源海底地震波數值計算中的應用[J].應用聲學，29（5）：358-363.

唐暉，李小軍，李亞琦.2012.自貢西山公園山脊地形場地效應分析[J].振動與沖擊，31（8）：74-79.

唐暉，李小軍，周國良.2016.散射問題求解中消除多次透射公式漂移失穩的一種措施[J].巖土工程學報，38（5）：952-958.

謝志南.2014.透射邊界零頻飄移失穩數值解增長模式解釋[J].地震工程與工程振動，34（4）：15-20.

徐建平，孔戈，周健.2008.接頭形式對聯絡通道抗震性能影響的研究[J].工程抗震與加固改造，30（2）：57-62.

楊光，劉增武.1994.地下隧道工程地震動分析的有限元-人工透射邊界方法[J].工程力學，11（4）：122-130.

章旭斌，謝志南.2017.離散網格中瑞利阻尼對波動的影響分析[J].地震工程與工程振動，37（1）：141-148.

周正華，廖振鵬.2001.消除多次透射公式飄移失穩的措施[J].力學學報，33（4）：550-554.

周正華，廖振鵬.2004.修正算子γB_0^0的物理含義解釋[J].地震工程與工程振動，24（5）：17-19.

Liao?Z?P，Wong?H?L.1984.A?transmitting?boundary?for?the?numerical?simulation?of?elastic?wave?propagation[J].Soil?Dynamics?and?Earthquake?Engineering，3（4）：174-183.

Analysis?on?Measures?of?Eliminating?Drift?instability?of?Multi-transmissionFormula?in?Solving?Scattering?Problems

TANG?Hui1，LI?Xiaojun2，3

（1.Nuclear?and?Radiation?Safety?Center，MEP，Beijing?100082，China）（2.College?of?Architecture?and?Civil?Engineering，Beijing?University?of?Technology，Beijing?100124，China）（3.Institute?of?Geophysics，China?Earthquake?Administration，Beijing?100081，China）

Abstract

Abstract：For?solving?the?wave?scattering?problems?with?Multi-Transmitting?Formula，the?effects?of?the?real-time?order?reduction?method，the?modified?operator?method，the?adding?visco-elastic?elements?method?and?the?improved?wave?input?method?on?eliminating?drift?instability?and?on?computation?accuracy?are?compared?and?analyzed?to?provide?useful?reference?for?engineering?application?of?this?artificial?boundary.The?results?show?these?four?methods?can?effectively?eliminate?the?relatively?slow?drift?instability?phenomenon;when?the?instability?trend?is?strong，the?modified?operator?method?and?the?adding?visco-elastic?elements?method?cannot?depress?the?instability?effectively.The?low-frequency?errors?may?be?introduced?by?the?real-time?order?reduction?method?when?the?damping?is?small.Under?the?premise?that?the?values?of?parameters?can?be?determined?appropriately，the?modified?operator?method?and?the?adding?visco-elastic?elements?method?can?improve?the?calculation?accuracy?of?low-frequency.The?improved?wave?input?method?can?depress?drift?instability?and?improve?calculation?accuracy?without?setting?parameters?artificially.

Keywords：Multi-Transmitting?Formula;drift?instability;measures?of?eliminating?drift?instability