粒子群優化算法對吸波結構材料優化研究*

鄭日升，張春林

(1.北京電子工程總體研究所，北京 100854；2.陸軍北京軍事代表局駐北京地區軍事代表室，北京 100854)

0 引言

為提高飛行器的突防能力和生存能力，現代的飛行器都采用氣動外形隱身和材料隱身降低飛行器的雷達散射截面(radar cross section，RCS)。吸波結構材料是材料隱身技術一種有效的方法，將吸波劑加入到復合材料中，不僅具有電磁波吸收能，而且不會受到結構受力的材料的影響[1]。

吸波結構隱身材料都要求反射率低，吸波能力強，阻抗匹配效果好，要求相應的材料具有隔離層厚度薄，而且質量小等特點[2]。隨著研發技術的不斷進步，已經有多種新型吸波結構隱身材料被應用于各種飛行器中，在軍事領域也得到了大量的應用[3]。在目前研制的新型材料中具有各向異性特性的材料也開始得到應用[4-7]。典型的美國隱身飛行器如F-22，在翼面和進氣道等區域采用了高性能吸波結構復合材料，有效地減縮了飛行器的RCS值[8-9]。以頻率點上的反射率作為優化目標函數，獲得了多層吸波結構材料的優化設計方法[10]。在研發新型材料過程中，大量的優化算法也應用于材料參數優化中。遺傳算法具有全局最優的搜索能力，因此在材料優化中應用較為廣泛，為材料測試提供了基礎。文獻[11-12]以天線罩壁等效平板結構為優化目標，頻率為600 MHz,針對多層介質的厚度進行優化，并得到了較好的優化效果。文獻[13]基于幾類典型材料,以吸收頻帶寬為目標,在給定厚度下對RAM進行了優化設計。文獻[14-15]優化得到的吸波材料具有頻帶寬、厚度薄的特點,獲得了較好的優化效果。本文首先基于吸波結構材料隱身特性，采用粒子群算法和遺傳算法，針對三層吸波結構隱身材料進行優化研究。

1 吸波結構材料反射率計算方法

1.1 反射率計算方法

圖1是典型的Jaumann多層吸波結構，其中金屬板在最底層，在底板上層是厚度d(mm)和電阻抗R2(Ω)。

其中，各層吸波材料的輸入阻抗可由式(1)得到：

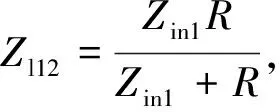
(1)

其中:R為電阻；Zin1為輸入阻抗，Zl12為負載阻抗，即任何一個電氣元件都有一定的阻抗，相對于電源而言，該阻抗就是負載阻抗。

多層吸波材料對電磁波的反射特性可由功率反射率(簡稱反射率T)由下面2個計算公式得到：

(2)

P為反射系數，轉化為反射率T公式為

T=20lg|P|.

(3)

1.2 單層Salisbury吸波屏反射率研究

下面是針對Salisbury吸波屏反射率進行分析，Salisbury吸波屏是指單層吸波材料放到金屬基體上。單層吸波材料隔離層厚度為1/4隔離層介質波長，即7.5E-3 mm，電阻R=377 Ω的反射率，頻率帶寬2～18 GHz，從圖2中可以看出，反射率T在入射頻率約10 GHz時反射率最小，但是頻率帶寬較窄。目前，對于結構型吸波材料很少采用Salisbury吸波屏，主要是單層吸波結構材料頻帶較窄，不適用于現在寬雷達頻率捕捉范圍，在工程方面單層吸波屏已很少采用。

基于以上的分析，下面針對3層Jaumann吸波結構材料進行初步分析，對電阻抗，隔離層厚度和介電常數進行優化研究，文章以吸波材料的頻寬為目標函數，針對粒子群優化算法構造目標函數。

2 粒子群優化算法目標函數構造

實際上各層吸波材料的介電常數ε、電阻抗R、介質的厚度d均是頻率的某種函數關系，所以反射率就是關于介電常數、材料電阻和各層厚度的函數，可記為

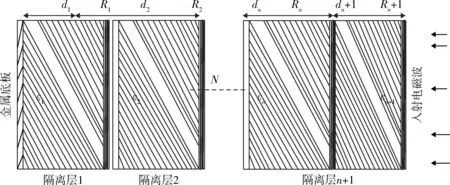
圖1 多層吸波結構材料簡化圖Fig.1 Sketch of multi-layer absorbing structure material

Z=F(ε，R，d1，d2，…，dn)，

(4)

式中：Z為材料的不同組合方式。

考慮在頻率區間[fa,fb]上的反射率曲線，當多層吸波材料在指定頻率區間內達到最佳吸波效果時，得到相應的材料參數，本文取反射率T<-15 dB條件下，反射率總和取最小值，即反射率曲線與頻率軸圍成的區域的面積應是最小值，如圖3所示。

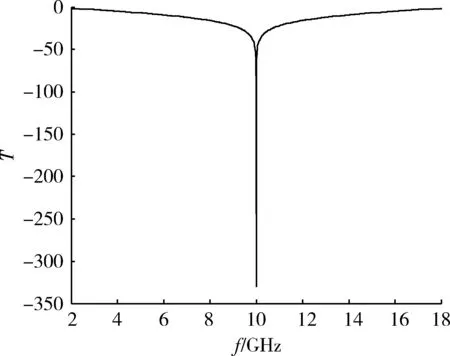
圖2 單層Salisbury反射率Fig.2 Single Salisbury reflectivity

圖3 吸波材料的反射率總和面積示意圖Fig.3 Sketch of the reflectivity of absorbing structure material

令

詩與詞是有區別的。二者形式上的區別顯而易見：詩，尤其是近體詩，或七言或五言，或仄起或平起，整齊而規則；詞就不一樣了，幾百個詞牌子，常用的也有幾十個，長的百余字，短的幾十字，句子長短不一，用韻寬，有的一韻到底，有的還中間轉韻，比如《菩薩蠻》。

,

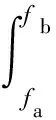
(5)

則求面積S的極小值內的頻率帶寬為目標函數，即確保T<-15 dB條件下，在頻帶寬內的反射率面積最小。

3 粒子群優化算法和遺傳算法介紹

3.1 粒子群優化算法

首先將粒子群優化算法應用到多層吸波材料優化設計，將所要求頻帶內整體反射率最小，將反射率T<-15 dB條件下的頻率帶寬為目標函數，在指定吸波材料厚度和電阻以及介電常數約束的情況下，準確計算出最優的多層吸波材料組合。由于多層吸波結構材料目標函數是求解一個極值問題，因此可以用粒子群優化算法來優化研究。

粒子群優化算法基本流程可描述為：

(1) 初始化：隨機生成M個粒子Xi和速度vi，當前最佳位置Pbesti=(Pbesti1,Pbesti2,…,Pbestin)得到粒子的初始種群t0。

(2) 給定參數：慣性因子ω，加速因子C1和C2，種群大小N，最大迭代次數Dmax。

(4) 進化出新的粒子：由上述列出的PSO粒子生成M個新粒子。

(5) 目標粒子的選擇：計算粒子群t1中的粒子的適應度值，若該粒子適應度值比父代差，則拋棄，否則保留該粒子形成新一代粒子群體。

(6) 是否結束運算，若滿足所求問題的要求或已達到最大迭代次數，則終止搜索，否則繼續進入循環迭代，更新粒子。

3.2 遺傳算法

遺傳算法采用比例選擇方法，單點交叉算子作為交叉算子，選用基本位變異算子作為變異算子。基于遺傳算法的多層吸波材料優化初始參數設置為：種群大小M為600，運行代數迭代范圍為0～600，交叉概率G為0.10～0.99，變異概率G1為0.001～0.100。

4 吸波結構材料優化

基于以上分析，本算法定義種群數量為0～600，種子數越多，越有可能收斂到全局最優值，但算法收斂速度慢。頻率范圍2～18 GHz，以0.01 GHz為間隔的速度向目標移動，最大速度取變化范圍的10%～20%，該范圍越小，收斂的分辨率越高，即不容易跳過最優值，但收斂慢；越大，收斂速度快，但可能跳出全局最優值。由于粒子群優化算法比遺傳算法更為簡單，沒有遺傳算法的交叉和變異操作，受到約束的變量較少，沒有許多參數需要調整。圖4和圖5表示粒子群優化算法和遺傳算法連續3次優化計算的反射率結果，發現連續3次優化結果相近，也就是說，粒子群優化算法能夠一次計算就能夠得到全局最優解。而遺傳算法3次優化得到的反射率具有較大的區別，穩定性差。

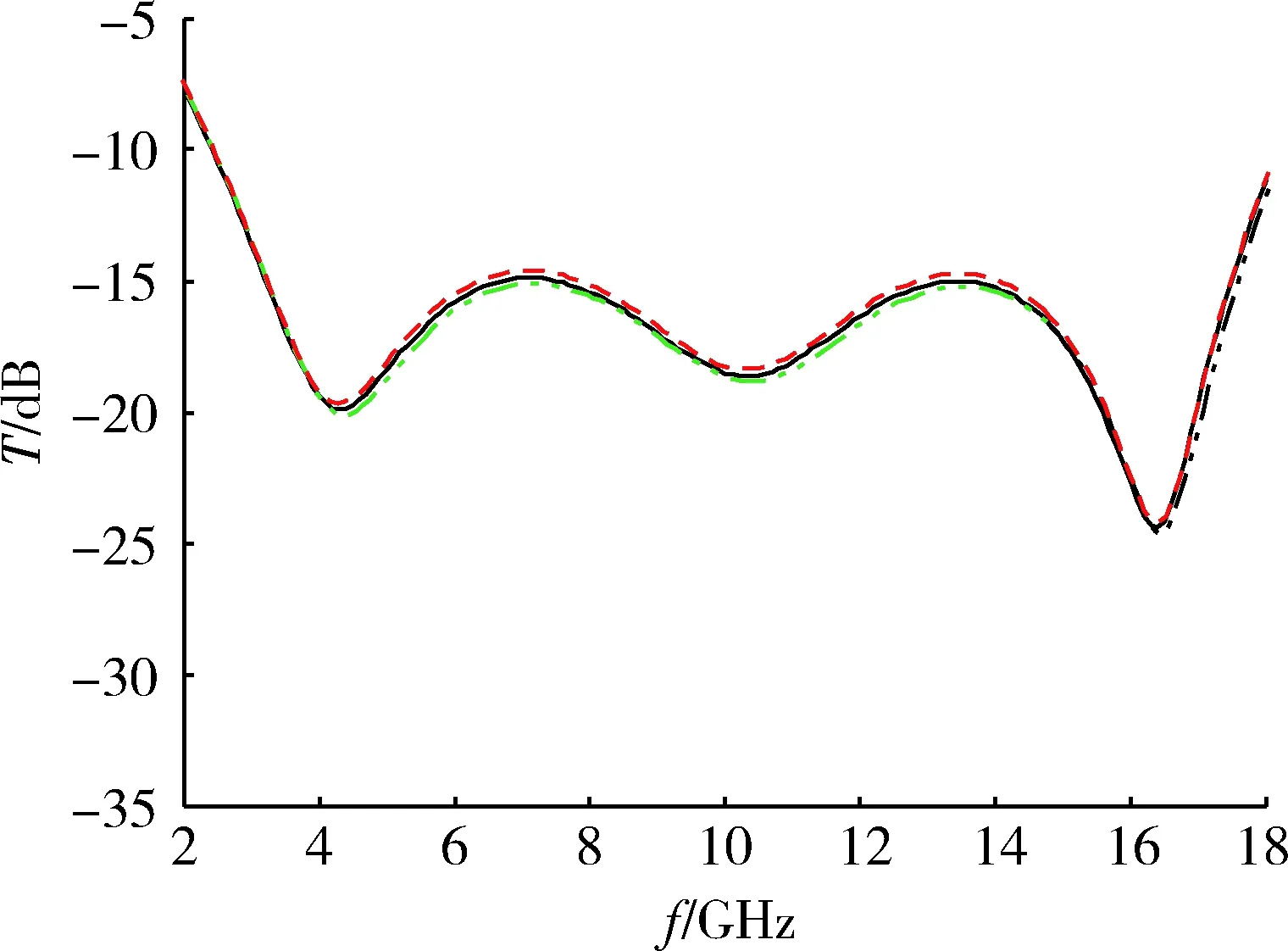
圖4 粒子群優化算法連續3次優化計算結果Fig.4 Results of the optimization with three consecutive of PSO algorithm

圖5 遺傳算法連續3次優化計算結果Fig.5 Results of the optimization with three consecutive of genetic algorithm

下面是遺傳算法和粒子群優化算法針對2層吸波材料在反射率T<-15 dB條件下，頻率帶寬的優化結果。通過頻帶寬發現，粒子群優化算法比遺傳算法頻帶寬約2 GHz。通過圖6中也可以發現，粒子群優化算法在不同頻率反射率總和也相對較小。

下面采用2種算法針對3層吸波材料反射率T<-10 dB進行優化比較，從圖7中發現，在2～8 GHz 2種算法反射率接近，整個頻率范圍內只有在2 GHz-10 dB。

接下來比較了反射率T<-20 dB條件下2種優化算法頻寬，相比圖8得到的結果發現，2種優化算法頻寬有較大的區別，在反射率相同的條件下，采用粒子群優化算法得到的頻寬比遺傳算法要大3 GHz，表明采用粒子群優化算法能得到較寬的頻寬。

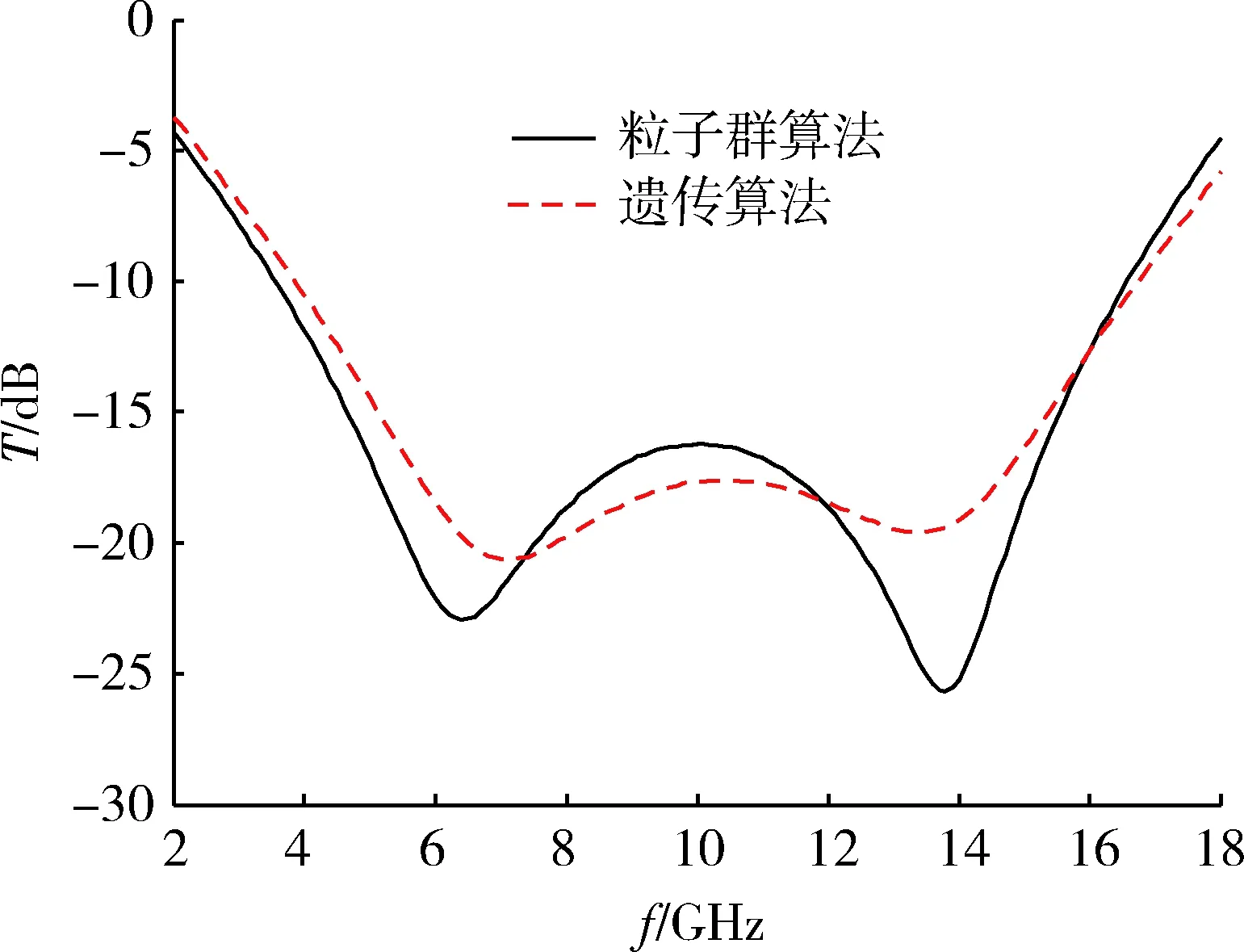
圖6 兩層吸波材料反射率T<-15 dB 2種優化 算法結果比較Fig.6 Comparison of two optimization algorithms for two layers of absorbing materials with reflectivity of T<-15 dB

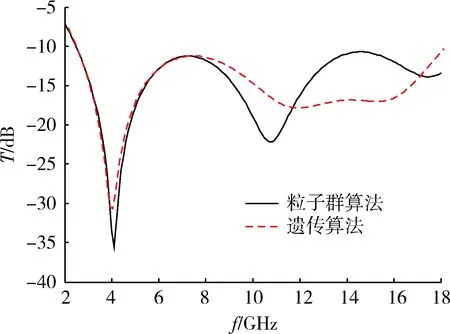
圖7 三層吸波材料反射率T<-10 dB 2種 優化算法分析Fig.7 Comparison of two optimization algorithms for three layers of absorbing materials with reflectivity of T<-10 dB

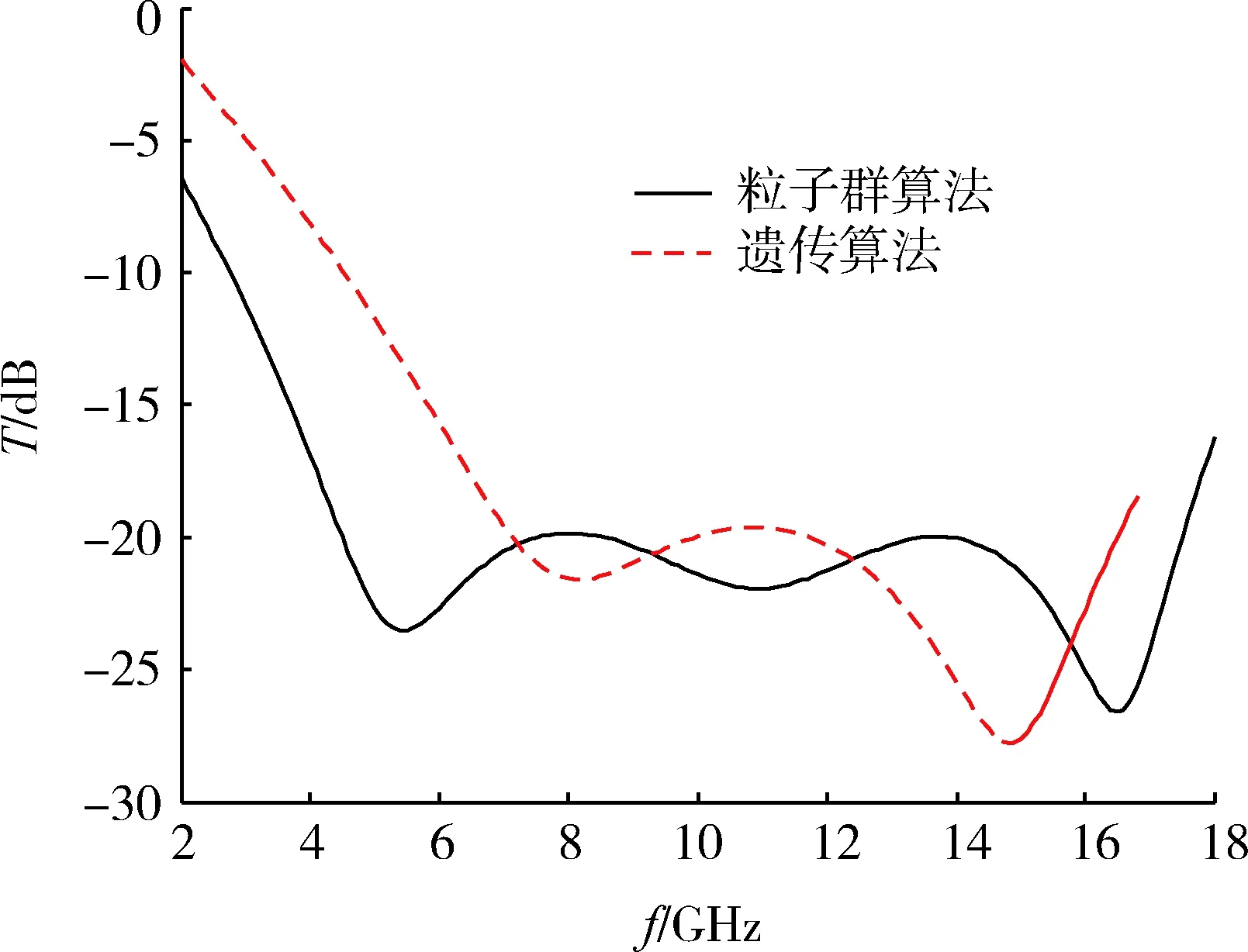
圖8 三層吸波材料反射率T<-20 dB 2種優化算法分析Fig.8 Comparison of two optimization algorithms for three layers of absorbing materials with reflectivity of T<-20 dB

針對3層吸波結構材料隱身優化比較發現，在反射率T<-15 dB條件下，粒子群優化算法頻率帶寬約在3 GHz～17.5 dB，遺傳算法頻率帶寬約在5～17 GHz范圍內，并得到了相應算法的介電常數，隔離層厚度及電阻的值，如表1所示，發現了粒子群優化算法的反射率總和小于2 dB。結果表明，在同樣優化條件下，采用粒子群優化算法能夠得到較寬的頻帶，如圖9所示。

表1 粒子群優化算法和遺傳算法優化參數比較Table 1 Optimization parameters of PSO and Genetic algorithm

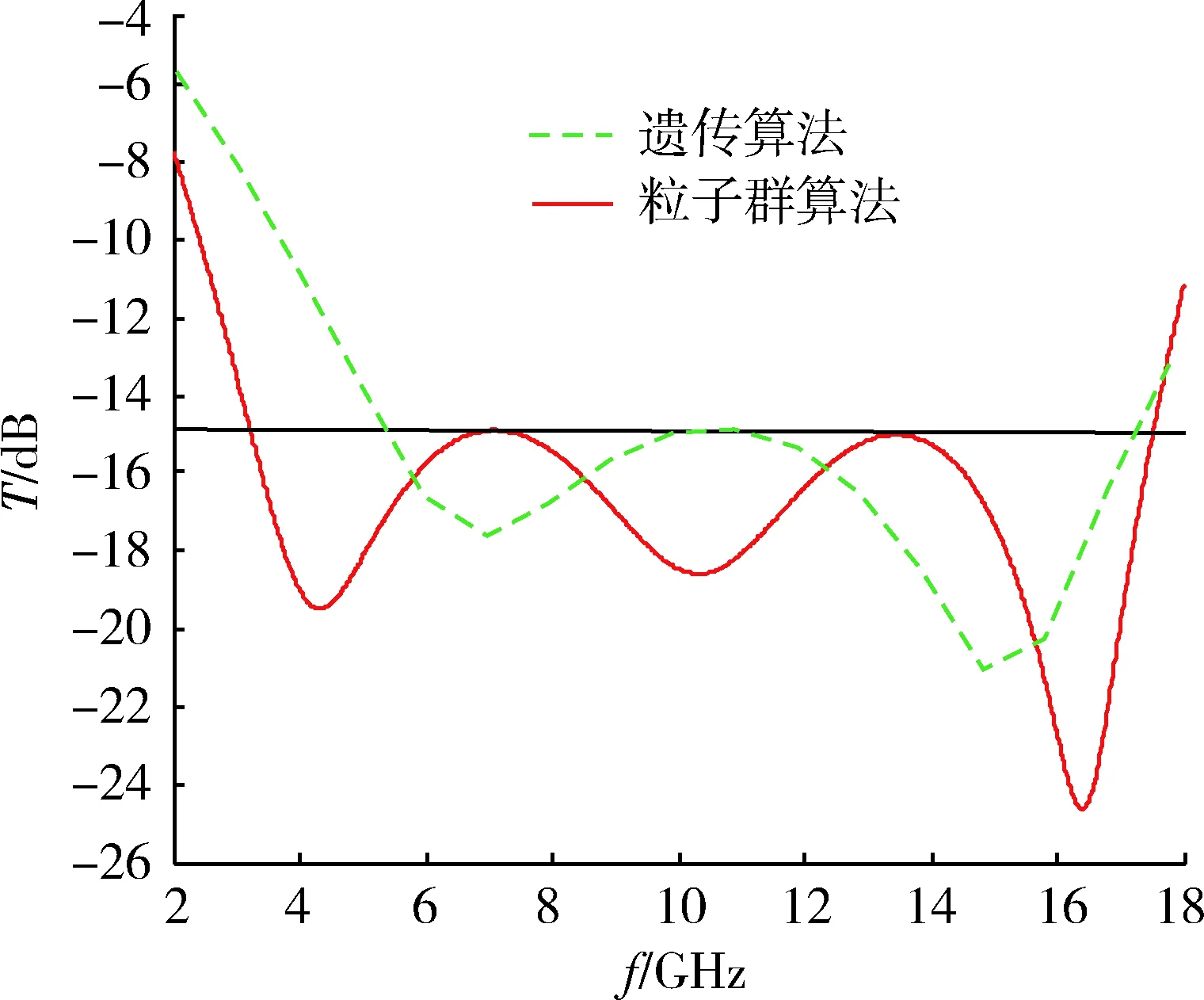
圖9 反射率T<-15 dB條件下粒子群優化算法和 遺傳算法頻率帶寬優化比較Fig.9 Comparison of frequency bandwidth optimization of particle swarm optimization algorithm and genetic algorithm with reflectivity of T<-15 dB

5 結束語

本文給出了采用粒子群優化算法針對吸波結構材料反射率頻帶的優化研究，比較了2種優化算法在不同反射率條件下的頻帶寬，發現了粒子群優化算法具有較寬的頻帶，并得出了以下結論：

首先，通過連續3次優化計算，在吸波材料反射率T<-15 dB條件下，發現遺傳算法優化得到的反射率具有較大的區別，比較了2層吸波材料反射率T<-15 dB的頻率帶寬，粒子群優化算法比遺傳算法頻帶寬約2 GHz，且得到了粒子群優化算法具有較好的穩定性。

其次，通過2種優化算法針對3層吸波材料反射率T<-10 dB和T<-20 dB進行優化比較，發現在2～8 GHz 2種算法反射率接近，整個頻率范圍內只有在2-15 dB；反射率T<-20 dB條件下2種優化算法頻寬，在反射率相同的條件下，采用粒子群優化算法得到的頻寬比遺傳算法要大3 GHz，表明采用粒子群優化算法能得到較寬的頻寬。

最后，在3層吸波材料反射率T<-15 dB約束條件下，對比了2種優化算法頻寬，發現采用粒子群優化算法具有較寬的頻帶，并得到了該反射率條件下粒子群優化算法比遺傳算法反射率總和要小2 dB。