改進禁忌-神經網絡在小電流接地系統選線中的應用
覃禹銘,任庭昊,胡兵軒,代啟璨,車 洵
(1.貴州電網有限責任公司遵義供電局,貴州 遵義 563000;2.南京南瑞繼保電氣有限公司,江蘇 南京 210000)
0 引言
我國10~35 kV電網大多采用小電流接地方式,地處南方雷雨潮濕環境,發生單相接地故障的概率很高,并有可能弧光接地發展為兩相短路。因此,迫切需要一種自動快速確定故障線路的方法,以保障電網穩定運行[1]。
不同故障條件下的有效故障特征分量差異較大。這是影響選線準確度的主要因素[2-4]。目前,選線方法有穩態法和暫態法。穩態故障分量一般較小,難以檢測[5-6]。暫態法的優點是故障特征分量明顯,但若采用單一判據,故障分量的差異會造成誤判[7-10]。為此,融合多種判據的選線策略得到了廣泛應用[11-14],其中大多采用反向傳播(back propagation,BP)網絡。
相較于BP網絡,徑向基(radial basis fuction,RBF)網絡的學習效率和逼近精度更高[15-16]。本文將RBF網絡應用于小電流接地選線,采用禁忌算法訓練RBF網絡,仿真驗證該方法的泛化性能和選線精度。
1 RBF網絡模型
本文采用單隱層前饋的三層RBF神經網絡結構,隱單元的激勵函數選用RBF函數。這里取高斯核函數。作為一種局部逼近神經網絡,隱單元輸出的線性加權和構成網絡輸出。RBF網絡模型如圖1所示。
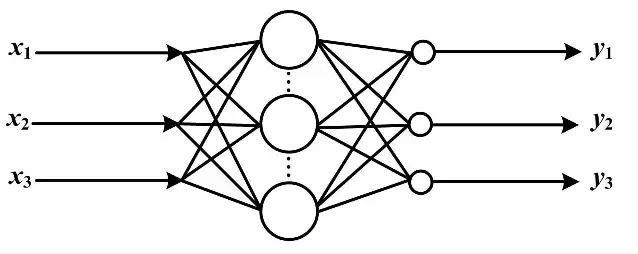
圖1 RBF網絡模型
網絡結構參數對于RBF網絡非線性逼近能力至關重要。網絡結構如果過于簡單,網絡對樣本的學習能力不夠;反之則容易導致過度擬合,降低神經網絡的泛化能力。特別在面對小電流接地系統復雜多變的故障狀況時,容易出現選線誤判的情況。因此,對RBF網絡結構參數的優化尤為必要。RBF網絡結構參數較多,但最關鍵的是隱含層與輸出層之間的連接權值,以及隱含層的中心和寬度。
2 禁忌算法優化RBF網絡
2.1 禁忌算法主要思想
容易陷入局部最優是BP神經網絡的主要缺陷。為了避免這一點,禁忌搜索(tabu search,TS)法模擬人腦智能,允許搜索方向背離目標函數,從而擴大了搜索范圍。但該方法同時帶來盲目搜索的問題。為此,引入禁忌表,其中保存了搜索歷史過程中移動的逆方向。這些移動在新的搜索中是被禁止的,從而回避無效搜索。禁忌表使得TS算法有效地跨越了局部最優的陷阱,但也可能誤將某些指向更優解的移動禁止。為了彌補這一點,又引入“藐視準則”,規定當某個移動可能尋找到更優解或該移動在禁忌表中的保存任期(禁忌長度)已到,則從禁忌表中釋放該移動。TS法的隨機搜索通過禁忌表的“禁止”和“藐視準則”的釋放,達到算法收斂性和種群多樣性之間的微妙平衡,其目的在于提高搜索效率的同時不錯過最優解。
2.2 關鍵參數及其改進
TS算法最重要的三個參數為鄰域范圍、禁忌條件和終止條件,分別對應搜索起始、中間和結束三個階段。
TS算法從初始解的鄰域開始搜索。鄰域范圍設置得大,搜索范圍廣,但搜索效率會降低;反之,鄰域設置過小,則無法保證搜索多樣性。因此,本文在優化的不同階段選取不同鄰域:起始階段應強調搜索多樣性,鄰域設置得大一些;最后階段搜索最優解、減小鄰域范圍、加強搜索強度,以便快速找到最優解。
搜索過程中,為了跳出局部極小的陷阱,禁忌表中禁止發生過的歷史移動。但一般均以移動的步長作為禁止條件。問題是,這一條件范圍太大。那些尚未訪問過的狀態點如果步長落入該范圍,也會被禁止,有可能錯過指向最優解的移動。為此,本文將禁止條件改為訪問過的狀態點及其步長,使禁忌范圍更精確地指向無效搜索。
逼近最優解的階段,迭代終止條件的確定將影響到優化時間和解的精度。如果以迭代數作為終止條件,雖然優化時間可以確定,但解的精度無法保證。如果以允許誤差為終止條件,可以滿足收斂精度,但優化時間可能較長;況且在最優解還未找到前,允許誤差僅是估計值。為了平衡優化時間和解的精度,本文采用迭代周期的辦法,在每個迭代周期中以本周期最優解和上周期最優解的優劣作為是否繼續迭代的判據。
2.3 改進禁忌算法訓練RBF網絡的步驟
禁忌算法尋優的主要過程可描述為:任選一初始解,從初始解的鄰域中隨機產生一系列新狀態,計算所有狀態的目標函數,找到對應最優目標函數的狀態,取為當前最優狀態;繼續迭代,一直持續到滿足設定的終止條件為止。其具體步驟如下。
①在定義域N(X)任選初始解X,設所有移動的狀態點及其步長集合為B、禁忌表狀態點及其步長集合為J、迭代數設為N、初始化J=0、N=0,目標函數為f。
②對不在禁忌表J內的狀態點及其所有步長Bj∈B-J,從初始解X的鄰域隨機產生一個新狀態Z。
③計算X和Z的目標函數f(X)和f(Z)。若f(Z)>f(X),放棄新狀態Z,迭代數N=N+1,轉步驟②重新產生新狀態。
若對所有的新狀態Zi滿足f(Zi)>f(X),并且滿足終止條件,算法終止。
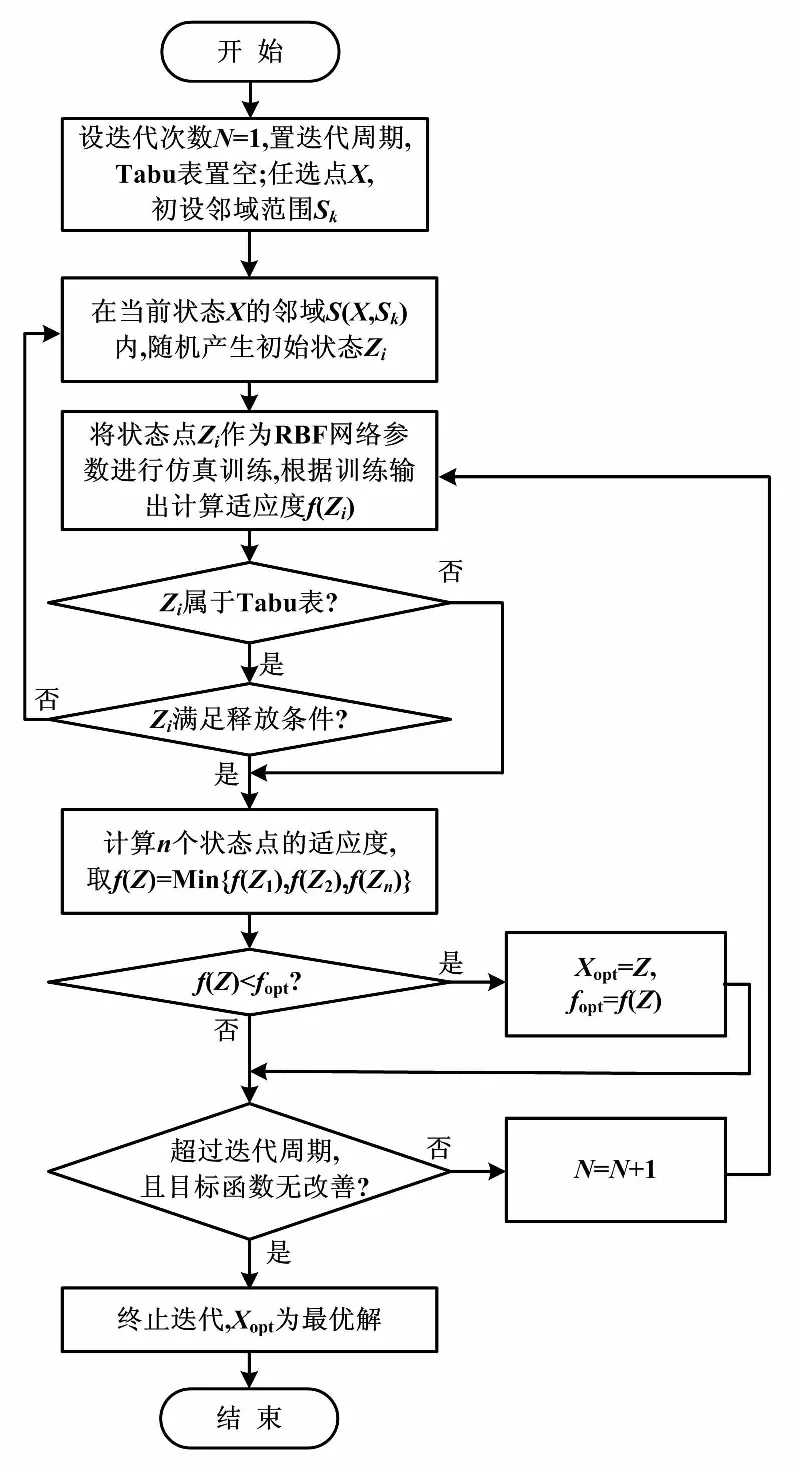
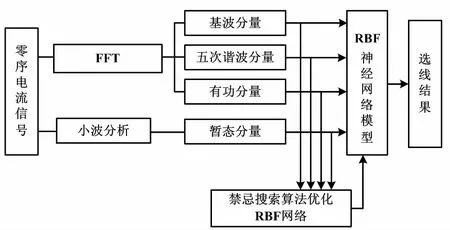
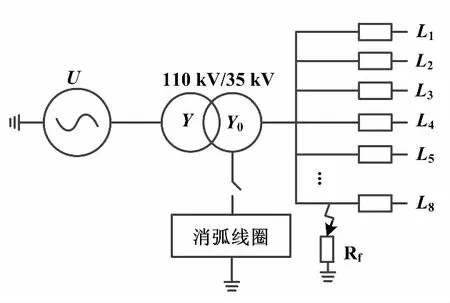
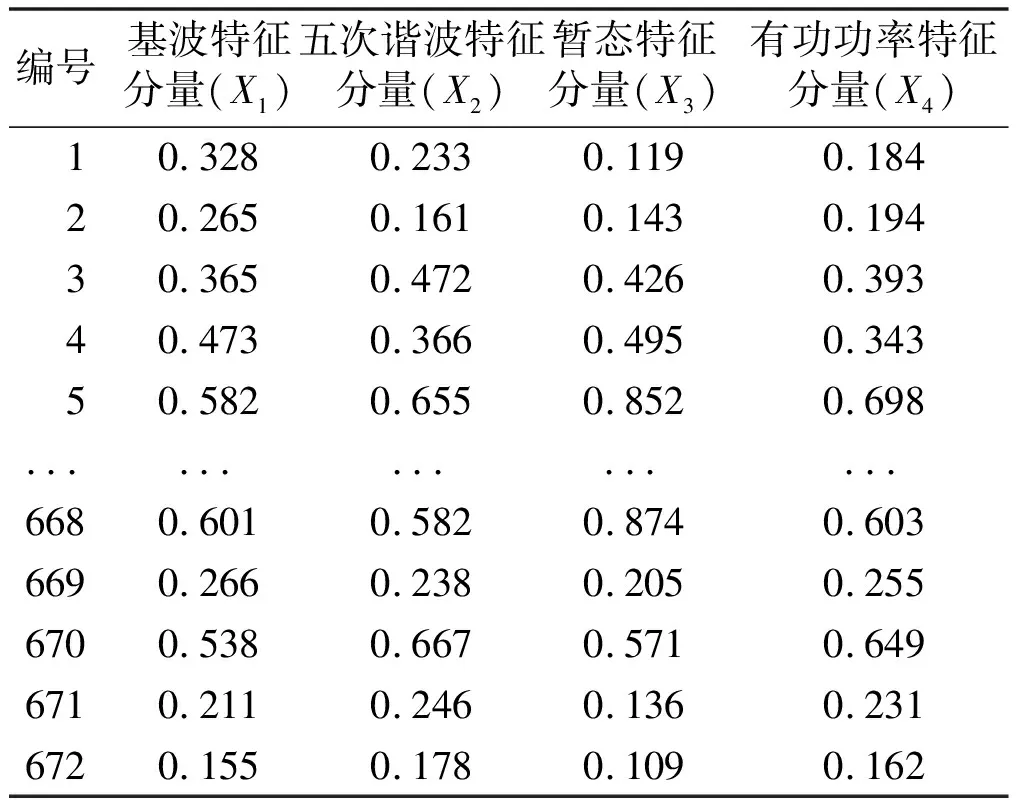
若f(Z) ④令X=Z,若所有點和步長都窮盡(B-J為空),則轉步驟⑤;否則轉步驟②。 ⑤若當前迭代周期內最優解精度低于上一周期(終止條件),則停止迭代;若不滿足迭代終止條件,將禁忌表清空(J=0),轉步驟②。 禁忌算法優化RBF網絡的評價目標是適應度函數。本文適應度函數以誤差平方和倒數的形式給出: (1) 改進禁忌算法優化RBF網絡流程如圖2所示。 圖2 改進禁忌算法優化RBF網絡流程圖 首先,在單相接地發生時采集零序電流的穩態和暫態有效故障特征,以區別故障和正常線路。穩態電流的采樣取故障發生三個周期后的信號,利用快速傅里葉變換算法(fast Fourier transform,FFT),得到零序穩態電流的有功分量、基波分量和5次諧波分量。對于暫態電流,則取故障前一周期和后一周期的信號,通過小波采樣法進行分解。本文采用db10小波包5層分解,提取出暫態能量特征值。每條線路的零序電流穩態特征和暫態特征作為一組故障錄入數據,構成神經網絡訓練和測試的樣本。這些樣本都經過歸一化處理。 其次,根據禁忌算法訓練神經網絡的步驟,輸入零序電流的穩態基波分量、5次諧波分量、有功分量及暫態能量特征分量,對神經網絡的結構參數進行優化,最終得到RBF網絡最佳的網絡層連接權值、隱含層的中心和寬度等參數。 最后,將故障測試數據同時輸入未經優化和優化后的RBF網絡,比較二者的選線準確率和效率。多判據融合選線模型如圖3所示。 圖3 多判據融合選線模型 ATP系統仿真模型如圖4所示。本文仿真模型為一個110 kV/35 kV的配電系統,變壓器35 kV側中性點經過一開關接消弧線圈。開關閉合與否構成中性點兩種運行方式:不接地或經消弧線圈接地。低壓側共8條架空出線。線路長度為:L1=5 km,L2= 10 km,L3=25 km,L4=20 km,L5= 35 km,L6= 30 km,L7=15 km,L8=40 km。線路正序參數為:感抗L1=1.51 mH/km,電阻R1=0.17 Ω/km,容抗C1= 9.70 nF/km。線路零序參數為:感抗L0=5.48 mH/km,電阻R0=0.23 Ω/km,容抗C0=6.00 nF/km。采樣周期設定為1×10-5s。 圖4 ATP系統仿真模型 每條線路發生單相接地故障采集的故障特征分量為4個。一次性將8條線路共32個故障分量輸入RBF網絡,經網絡計算后應得到8條線路的判斷結果。RBF網絡的輸入輸出容易決定,但中間隱含節點數直接影響網絡預測精度與效率,節點數并非越多越好。隱含節點數超過某一數值后精度不再有明顯變化,反而計算量會陡增。大量樣本的仿真測試表明,隱含節點數取為58是合適的。據此,3層RBF神經網絡的結構設為32-58-8。取768個樣本中的672個作為訓練樣本,剩余96個作為測試樣本。部分故障特征分量如表1所示。 表1 部分故障特征分量 禁忌搜索算法的參數設置如下:種群規模設為40,禁忌搜索迭代周期設為100,禁忌長度設為50,目標誤差設為0.02。為了比較RBF、傳統TS-RBF及改進TS-RBF這3種方法的選線效果,同時采用訓練樣本對3種網絡進行訓練。其目標是使網絡輸出的選線誤差小于設定的目標誤差。3種方法的網絡訓練誤差曲線如圖5所示。 圖5 網絡訓練誤差曲線 由圖5可知,改進TS-RBF網絡優化起始階段的收斂速度明顯快于RBF和傳統TS-RBF網絡,在迭代27次后即達到目標誤差;而傳統TS-RBF需要83次,RBF需要378次。同時,改進TS-RBF在收斂精度方面也明顯優于其他兩種方法。 對于3種訓練好的網絡,采用96個測試樣本進行驗證對比。網絡輸出接近1判定是故障線路,同時用網絡輸出與1的差值表達該網絡對故障線路的逼近程度;同理,非故障線路的網絡輸出越接近0,則表示網絡逼近精度越高。設定不同的試驗條件(補償度、短路點位置、合閘角和接地電阻),分別采用3種選線方法進行仿真試驗,并比較3種算法的輸出數值。對于正常線路,改進TS-RBF輸出最逼近0,其次是傳統TS-RBF,單純RBF對0的偏差最大;對于故障線路,改進TS-RBF輸出對1的偏差最小,其次是傳統TS-RBF,單純RBF偏差最大。從最終選線結果比較,共96個測試樣本中單純RBF出現8例誤判,傳統TS-RBF出現3例誤判,而改進TS-RBF僅有1例誤判。 3種網絡的預測誤差比較曲線如圖6所示。 圖6 3種網絡的預測誤差比較曲線 經統計:改進TS-RBF、傳統TS-RBF和單純RBF三者的選線準確率分別為98.9%、96.9%和91.7%,證實了改進TS-RBF的準確性。 鑒于RBF網絡預測能力與其參數密切相關,本文應用改進的TS法優化RBF神經網絡,優化誤差曲線和最終選線結果都證實了改進TS-RBF網絡相較于傳統的TS-RBF,自學習能力和魯棒性更強。 本文以110 kV/35 kV的配電系統作為仿真實例。為避免單一判據的誤選和漏選,融合多種故障分量信息,實現對故障信號更精準的描述;結合改進的TS-RBF網絡,構成多判據選線模型。仿真結果表明,該模型的選線準確率達到98.9%,且不受多種故障條件的干擾。
3 融合選線模型
4 仿真實例
4.1 系統建模
4.2 網絡訓練
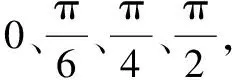
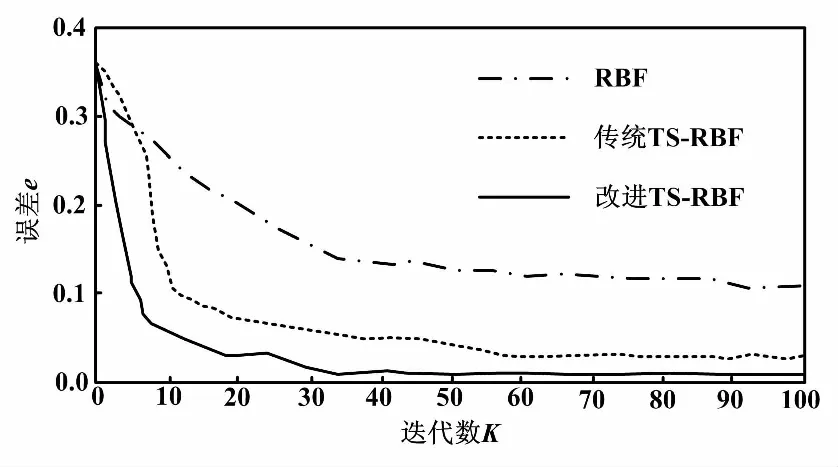
4.3 模型驗證
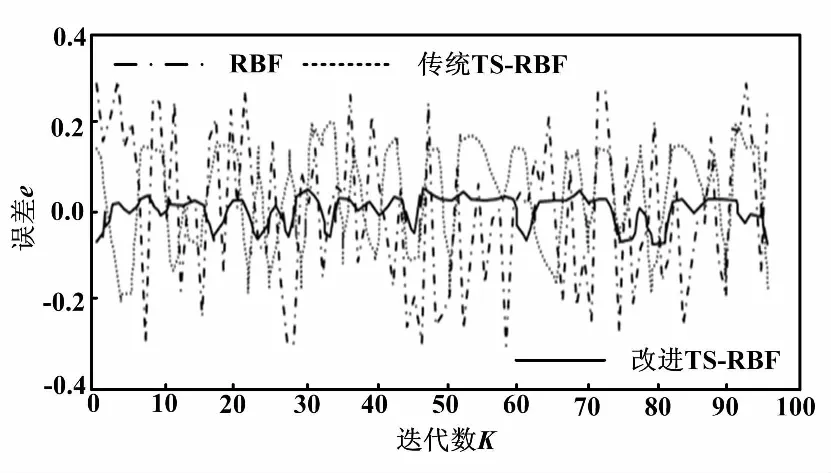
5 結束語

