高超聲速飛行器魯棒多目標線性變參數控制

蔡光斌， 趙陽， 張勝修， 楊小岡

(1.火箭軍工程大學 導彈工程學院, 陜西 西安 710025； 2.西北工業大學 航天學院, 陜西 西安 710072)

0 引言

高超聲速技術被稱為21世紀航空航天技術的“制高點”[1-2]，其是當前以及未來航空航天領域發展的核心技術之一[3]，特別是具有“乘波體”構型的吸氣式高超聲速飛行器，被認為是一種未來進入太空更經濟有效的方式，因其重要的戰略意義而備受世界各軍事強國的廣泛關注[4]。

吸氣式高超聲速技術的發展始于20世紀50年代提出的高超聲速燃燒概念[2-3]。經過幾十年的發展，美國、俄羅斯、法國、德國、英國、日本和印度等國自20世紀90年代以來已在高超聲速技術方面陸續取得了重大進展，并相繼開展了多項地面試驗和飛行試驗[3-5]。目前，高超聲速技術已經從早期的概念和原理探索階段進入到以高超聲速巡航導彈、高超聲速飛機和空天飛機等為應用背景的先期技術開發階段和工程研制階段。對于高超聲速飛行技術的研究，我國起步較晚，在21世紀以前，我國的研究主要集中于基礎性的研究。2014年，我國自主完成首次高超聲速風洞實驗，結束了60多年的國外技術壟斷[4-9]。近年來，我國正在緊鑼密鼓地進行“乘波體”高超聲速飛行器的自主研制和飛行試驗工作，并取得了一系列的突破性進展。

與傳統的飛行器相比，吸氣式高超聲速飛行器由于采用超燃沖壓發動機、機體/發動機一體化設計技術，導致其氣動特性、推進系統與結構動態之間存在明顯的耦合效應[6-9]；同時，高超聲速飛行器的飛行包線范圍更大，飛行環境更加復雜，存在各種隨機干擾和擾動，使控制系統隨飛行區域的變化呈現出強烈的非線性和嚴重不確定性[10]；此外，由于高超聲速飛行器的快速飛行，使得其所攜帶的燃料迅速消耗，從而引起高超聲速飛行器的質量分布快速變化，使高超聲速飛行控制系統具有明顯的快時變性[3]。因此，高超聲速飛行控制系統具有強非線性、強耦合性、快時變性以及嚴重的不確定性。

目前，國內外學者在高超聲速飛行器的飛行姿態控制技術方面已取得了一系列的研究成果，從控制方法角度出發，可分為以下3類：基于線性模型的控制方法、基于非線性模型的控制方法、基于線性參變/時變模型的控制方法。文獻[11-12]所采用的控制方法就屬于第一類控制方法，該類方法對模型的精度要求較低，有利于系統的穩定性分析與控制性能設計，但對于具有快時變、強耦合、強非線性以及嚴重不確定性的高超聲速飛行控制系統而言，一般基于線性化的控制設計方法均存在著不同程度的局限性。例如：現有的線性控制設計一般只是基于系統的某個平衡工作點附近的線性化模型來設計局部控制器，而對于非平衡點處或者非設計區域無法實現對飛行器的大跨度機動飛行控制；文獻[13-14]所采用的控制方法屬于第二類控制方法，該類方法更加符合高超聲速飛行控制系統的非線性模型本質，但對模型的結構和精確性要求更高，且不易做魯棒性分析。這對于具有較強的參數與結構不確定性和未建模動態的高超聲速飛行器控制系統設計而言，限制了許多非線性方法的應用。例如，許多非線性控制設計是基于反饋線性化模型展開的，但是對于大多數高超聲速飛行器模型而言，通常不滿足反饋線性化條件的，一般都是加入多個較強的假設條件才能實現反饋線性化。然而，即便是對可反饋線性化的系統，反饋線性化后得到的高階李導數求解過程和表達式都極為復雜，后續設計過程中無法在此基礎上展開諸如魯棒性、自適應性等控制性能分析[15]。

基于線性參變模型的控制方法實質上是利用線性控制方法對非線性系統進行控制器設計，其最大優點是控制器本身為參數依賴，可以進行自增益調節，而且魯棒穩定性可以從理論上得到保證，如文獻[16-23]，都屬于該類控制方法，因此本文采用該類控制方法設計高超聲速飛行器姿態控制系統。

對于具有快時變、強耦合、強非線性、嚴重不確定性的高超聲速飛行控制系統而言[3]，所設計的控制器必須具備魯棒穩定性、干擾抑制能力和一定的動態跟蹤特性。H∞控制器在系統出現不確定性時具有較好的魯棒穩定性，但這是以犧牲其他指標為代價的，最終的控制系統性能仍難以滿足要求[17]；而H2性能對于處理隨機噪聲、干擾很有效，但控制效果完全依賴于描述被控對象數學模型的精確性，這點影響了傳統H2最優控制器在實際中的應用[18]；極點配置通過將閉環系統的極點配置到指定區域內，就能保證系統具有一定的動態特性[21]。因此，本文在得到吸氣式高超聲速飛行器剛性線性變參數(LPV)模型的基礎上，針對其縱向飛行姿態控制問題，提出了一種基于區域極點配置的H∞/H2多目標LPV控制系統設計方法，較之傳統的H∞控制器與H2控制器，該方法對控制系統模型的精確性要求不高，且不僅可以保證閉環系統的穩定性，而且還使所設計的跟蹤控制器具有較好的魯棒性和動態特性；同時，通過引入松弛變量，降低了所設計控制器的保守性。最后通過與現有文獻[23]中的方法進行仿真對比，說明了所設計控制器的有效性和優越性。

1 縱向LPV建模

1.1 吸氣式高超聲速飛行器縱向機理模型

吸氣式高超聲速飛行器縱向平面的詳細幾何尺寸可以參照文獻[3-4,7]。根據普朗特- 邁耶爾理論，應用拉格朗日方程，可以得到吸氣式高超聲速飛行器縱向非線性機理模型[3-4]：

(1)

式中：v為飛行速度；h為飛行高度；α為攻角；γ為飛行路徑角；Q為俯仰角速率；T、D、L、Myy分別表示推力、阻力、升力、俯仰力矩；m為飛行器質量；μ為地球引力常量；r為飛行器質心到地心的距離；Iyy為俯仰轉動慣量。上述各力與力矩系數以及相應的氣動力與力矩系數表達式為

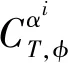
1.2 剛性LPV模型

針對機理模型(1)式，忽略飛行器的彈性效應，在后續的控制器設計中，將其視為模型的不確定性[3-4]。為了得到LPV模型，首先選取調度變量θ=[Ma,h]T，在馬赫數Ma∈[8,10]，飛行高度h∈[24 672,30 840]的飛行包絡內進行網格劃分，并對網格上的每個點進行配平得到平衡狀態點，從而得到圍繞平衡狀態的增量模型，然后采用雅克比結合張量積的方法可以得到具有多胞結構的剛性LPV模型，模型轉化的具體過程和主要思路參見文獻[20]。這里，給出增量形式的LPV模型如下：

(2)

式中：xν=[vν,hν,αν,γν,Qν]T代表飛行狀態圍繞平衡狀態的增量，vν、hν、αν、γν、Qν分別為飛行速度、飛行高度、攻角、飛行路徑角、俯仰角速率圍繞平衡狀態的增量；uν=[δeν,δcν,φν,Adν]T代表控制變量圍繞平衡狀態的增量，δeν和δcν分別為升降舵偏角和鴨翼舵偏角圍繞平衡狀態的增量，φν為等效燃料率的增量，用于控制發動機推力大小，Adν為擴散區比例的增量，用于控制發動機的進氣量，從而間接控制推力；A(θ)、B(θ)分別為

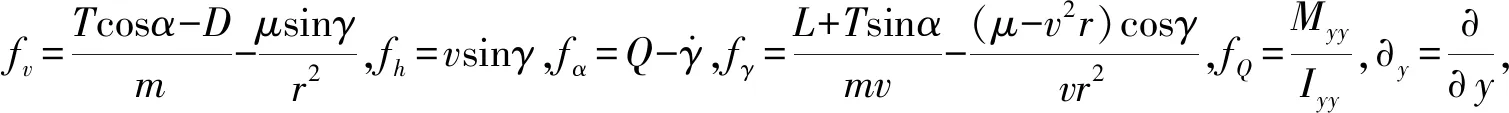
注釋1在后續內容中，將針對上述高超聲速飛行器的多胞LPV模型進行控制器設計。下節中，將考慮更一般化的多胞LPV系統，提出連續時間多胞LPV系統的變增益H∞/H2控制器設計理論方法。其中，將在一般化的多胞LPV系統中引入了干擾輸入量，這類干擾輸入可以作為高超模型和參數不確定性、高超彈性模態影響等輸入項。

2 基于區域極點配置的混合多目標LPV狀態反饋控制

2.1 問題描述

考慮如下多胞LPV系統S：

(3)

式中：A(θ)、Bi(θ)、Ci(θ)、Di(θ)均為LPV系統S的相容矩陣；x∈Rn為狀態向量，w∈Rl為干擾輸入，u∈Rm為控制輸入，z∞∈Rn1為H∞性能指標下的控制輸出，z2∈Rn2為H2性能指標下的控制輸出，n、l、m、n1、n2表示向量維數且相容。針對LPV系統S，設計如下狀態反饋控制律：

u=K(θ)x，

(4)

式中：K(θ)∈Rm×n. (4)式代入到(3)式中，可以得到如下閉環LPV系統CDOF：

(5)

式中：系數矩陣Acl(θ)、C1cl(θ)和C2cl(θ)分別為

Acl(θ)=A(θ)+B2(θ)K(θ) ，

(6)

C1cl(θ)=C1(θ)+D12(θ)K(θ)，

(7)

C2cl(θ)=C2(θ)+D22(θ)K(θ).

(8)

問題1針對(3)式中的多胞LPV系統S，設計形如(4)式中的LPV狀態反饋控制器，使得(5)式中的閉環LPV系統CDOF對所有的調度參數滿足如下特性：

1)穩定性能：系統的閉環極點配置到復平面左半平面上指定的圓形線性矩陣不等式(LMI)區域(如圖1所示，LMI區域的具體定義詳見參考文獻[21-22])，使Acl(θ)穩定；同時使閉環系統CDOF具有一定的動態性能。

圖1 圓形LMI區域Fig.1 Circular region of LMI[21-22]

2)H∞性能[22]：對于能量有界輸入信號w∈L2，給定性能指標γ>0，使得由w到z∞的傳遞函數矩陣Tz∞w(s)的H∞范數|Tz∞w(s)|∞<γ.

3)H2性能[22]：對于隨機干擾輸入信號w，給定性能指標η>0，使得由w到z2的傳遞函數矩陣Tz2w(s)的H2范數滿足|Tz2w(s)|2<η.

2.2 基于區域極點配置的H∞/H2LPV控制

為了解決問題1，首先給出如下引理：

(9)

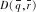
(10)

式中：*表示由對稱矩陣的對稱性得到的塊矩陣(以下情形類似，不再重復說明)。

(11)

(12)

trace(Q)<η2.

(13)

引理4[16]下列條件等價：

2)存在矩陣G使得下式成立：

通過引入松弛變量G，使得在變量和約束增維的空間中，產生了擴展條件，可以實現Lyapunov函數矩陣與系統矩陣解耦。

根據文獻[23]中的思想，易將引理1～引理3從LTI系統推廣到多胞LPV系統，結合問題1，給出如下定理：

定理1針對(3)式中的多胞LPV系統S，給定正標量γ>0和η>0，存在形如(4)式中的增益調度狀態反饋控制器，使得閉環系統CDOF滿足問題1中3個特性的充分條件為存在正定對稱矩陣X，對稱矩陣Q和矩陣Li，i=1,…,N，j=1,…,N，假設各矩陣之間維數是相容的，且滿足如下LMI約束條件：

trace(Q)<η2，

(14)

(15)

(16)

(17)

(18)

(19)

Ξij=

(20)

若(14)式～(20)式有解，則狀態反饋調度增益K(θ)可由(21)式求得：

(21)

證明(6)式～(8)式中的閉環系數矩陣代入(9)式、(10)式和(12)式的左邊，分別得：

(22)

(23)

(24)

令XD=X∞=X2=X，并引入新的矩陣變量L(θ)：

(25)

根據LPV系統的多胞特性， (22)式～(24)式可分別化為

Γ(θ)=

(26)

(27)

(28)

注釋2定理1由于計算簡單，計算量小，能簡化系統分析與綜合過程，所以應用起來很方便。同時注意到定理1中的LMI約束不僅僅對矩陣X、Q和矩陣Li是線性的，而且也是性能指標γ和η的線性約束，因此，定理1的求解條件就可轉化成具有LMIs約束的線性目標函數最小化問題。然而，在實際應用中，性能指標γ與η不可能同時達到最優，必須進行加權處理，常見的加權形式如下：

J=aγ+bη,

(29)

式中：a、b為權值，可以根據具體的設計要求進行設定。于是，定理1的求解條件變為

(30)

由定理1的證明過程可知，此定理實際上限制了XD=X∞=X2=X,而且還要求在所有的多胞頂點上只存在一個共同的Lyapunov函數矩陣，顯然，這給系統的綜合帶來了較大的保守性。對此，可以通過引入松弛變量的方法來降低保守性，即提出定理2如下。

定理2針對定理1中的設計要求，其可行的充分條件為存在正定對稱矩陣X∞i、X2i，正定矩陣XDi，對稱矩陣Qi和矩陣G1、G2、H1i、H2i,i=1,…,N，假設各矩陣之間維數是相容的，且滿足如下LMI約束條件：

trace(Qi)<η2,

(31)

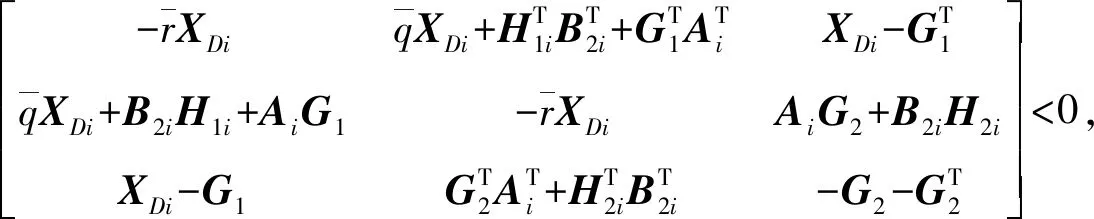
(32)

(33)

(34)

(35)

(36)

令

根據引理4，(12)式等價于(37)式：

(37)

令

(38)

根據引理4，(13)式和(14)式分別等價于(38)式：

(38)

(39)

由于問題1面向的是多胞LPV系統，根據凸優化理論可知，只要針對多胞的頂點進行控制器設計即可，于是，(6)式～(8)式在多胞模型頂點的表達形式為

Aicl=Ai+B2iKi,
C1icl=C1i+D12iKi,
C2icl=C2i+D22iKi.

(40)

(40)式帶入(36)式～(39)式中，并引入新的矩陣變量H1i=KiG1，H2i=KiG2，i=1,…,N，即可得到(31)式～(35)式的LMI約束條件。證畢。

注釋3定理2通過引入松弛變量，使Lyapunov函數矩陣與系統矩陣解耦，從而可以在不同的頂點上使用不同Lyapunov函數矩陣，降低了控制系統設計的保守性，但由于存在著KiG1和KiG2等矩陣變量的耦合項，因此是一個雙LMI求解問題，不能直接利用Matlab中的LMI工具箱進行求解，解算難度增大，計算量相對于定理1也大大增加，具體解法可參見文獻[24]。

注釋4由于KiG1和KiG2等矩陣變量之間存在著耦合項，其并不是LMI的典型形式，不能直接使用LMI工具箱求解。采用文獻[25-27]提出的錐互補線性化算法，可將其轉化為一些受LMI約束的序列優化問題來解決。故由錐互補線性化算法可將定理2中的求解條件轉化為如下所示的受LMI約束的最小優化問題：

(41)

若受LMI約束的最小優化問題(41)式可解，則定理2中的條件也是可解的，雖然不一定存在全局最優解，但是此最小優化問題也比雙線性不等式的求解過程容易得多。

3 數值仿真算例

3.1 控制器設計

應用第2節提出的基于區域極點配置的H2/H∞控制系統設計方法，來實現吸氣式高超聲速飛行器的跟蹤控制。首先，參照文獻[20]中的方法，將(2)式中的剛性LPV模型擴展成系統設計所需的(3)式的形式。

重新書寫(2)式中的狀態方程，表達形式如下：

(42)

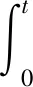
式中：xv表示參考輸入速度信號rv(τ)與實際速度v(τ)之差的積分；xh表示參考輸入高度信號rh(τ)與實際高度h(τ)之差的積分，以此擴展開環系統的狀態變量。

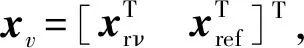
A(θ)xν+Bw(θ)w+Bu(θ)uν.

(43)

Cz∞xν+Dz∞uν,

(44)

(45)

(46)

z∞=C1(θ)x+D12(θ)u,

(47)

z2=C2(θ)x,

(48)

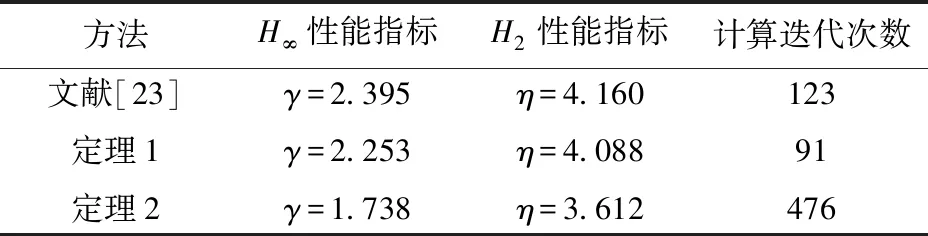
表1 魯棒性能指標

表2 各頂點的閉環極點

通過表1可以發現，定理1得到的兩個性能指標與采用文獻[23]中方法得到的性能指標相比很接近，降低幅度不大，但定理2得到的兩個性能指標都小于前兩種方法得到的，因此，可以驗證定理2確實降低了控制系統設計的保守性；同時，還可以看出，定理1的計算迭代次數是最少的，更適合實際工程應用，定理2的計算迭代次數明顯多于前兩種方法的迭代次數，而且計算結果還依賴于初值的選取，但對于目前計算機的計算速度來講，是能夠接受的。從表2可以看出，各頂點的閉環極點都配置到了圓形區域D(5,3)中，由多胞性質可知，剛性LPV系統的所有閉環極點都位于圓形區域D(5,3)中，可以使系統具有良好的動態特性。

為了綜合求解上述的問題，首先將系統(2)式轉化為多胞形式。參數依賴的系統矩陣A(θ)和B(θ)可以表示為

根據各頂點狀態反饋控制器K1、K2、K3、K4，可以得到剛性LPV模型增益調度狀態反饋控制器K：

K(Ma,h)=α1K1+α2K2+α3K3+α4K4.

(49)

3.2 非線性仿真與結果分析

為了驗證上述所設計控制器的有效性，基于Matlab/Simulink仿真環境，在h=26 518 m，Ma=8.8的平衡巡航條件下(Ma=8.8，v=26 353 m/s，α=1.47°，Q=0°/s，h=26 518 m，γ=0°，δe=11.953°，δc=-0.62°，φ=0.338，Ad=0.84)進行非線性仿真。

參考輸入信號rv(t)和rh(t)的形式[4]如下：

仿真結果如圖2、圖3所示。

圖2(a)、圖2(b)分別給出了在采用本文方法(定理1)與傳統方法(參考文獻[23])所設計控制器的作用下，標稱模型和引入參數不確定性后模型的速度和高度響應曲線。由圖2(a)、圖2(b)中可知，對于任一種模型，采用本文定理1所設計的控制器都能在6 s內跟蹤到參考指令輸入，而標稱模型在參考文獻[23]中傳統方法所設計控制器的作用下，需要10 s左右的時間才能跟蹤到參考指令輸入，且具有最大不確定參數模型的調節時間更長，因此采用定理1所設計控制器的動態性能要比采用參考文獻[23]中方法所設計控制器的動態性能好。兩種模型在采用定理1所設計控制器的作用下都能夠準確地跟蹤到參考指令輸入信號，同時，通過比較采用定理1所設計控制器作用下的兩種曲線可以發現，具有最大不確定參數模型的階躍響應比標稱模型的階躍響應調節過程長，且還出現了一定的超調，但都在合理范圍之內。此外，在進行非線性仿真過程中，引入了一定的外界干擾，但仿真結果中沒有出現被干擾的現象，因此說明所設計的控制器還具有較強的抗干擾能力。

圖2(c)～圖2(e)為其他狀態量在參考指令輸入信號作用下的變化曲線，從中可以看出，它們的大小均在有效范圍內變化，并且很快地趨近穩定。

圖2 速度跟蹤下的狀態階躍響應Fig.2 Step response of speed tracking

圖3(a)和圖3(b)為兩個舵偏角控制輸入的變化曲線，從中可以看出，輸入變量均在有效地范圍內變化，并且很快地趨近穩定，說明所設計的控制器能夠保證執行機構不會達到飽和效應。圖3(c)和圖3(d)分別為等效燃流率和擴散區比率的變化曲線。這兩個控制輸入的調節都會影響到發動機推力的變化。從圖3(c)可以看出，每當階躍輸入作用在閉環系統上時，等效燃流率都會迅速增加，最終趨于穩定值，其控制作用直接影響到高超聲速飛行器的實際速度與高度變化，實現了速度和高度的跟蹤控制。從圖3(d)可以看出，擴散區比率的變化曲線隨著階躍輸入信號的一次次升高而一次次的降低，最終達到穩定值，這正說明隨著飛行速度和高度的增加，高超聲速飛行器的發動機會自動調節擴散區比率的大小，來保證進入到燃燒室內的壓縮空氣具有一定的速度，從而保證了發動機的正常工作。

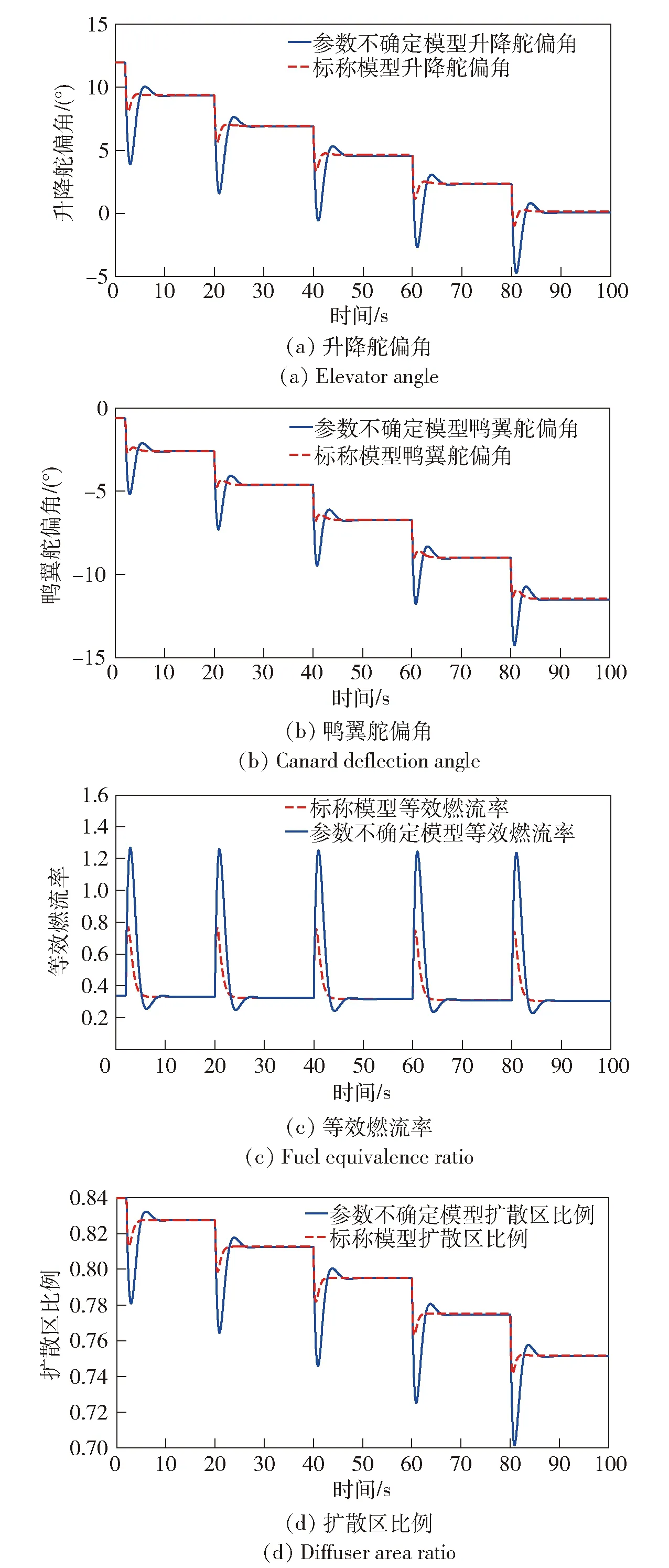
圖3 速度跟蹤下的控制輸入階躍響應Fig.3 Step response of control input of velocity tracking

4 結論

1) 針對吸氣式高超聲速飛行器的縱向飛行控制，本文建立了具有多胞結構的剛性LPV模型。針對此類模型，提出了一種基于區域極點配置的H∞/H2多目標LPV狀態反饋魯棒控制算法，通過理論上的嚴格推導，證明了此算法能夠實現系統的多目標控制。

2) 通過引入松弛變量的方法，降低了控制系統設計的保守性，最終得到了滿足期望性能指標要求的LPV狀態反饋魯棒跟蹤控制器。

3) 所設計的控制器應用在高超聲速飛行器非線性機理模型上，通過仿真驗證了所設計的控制器有效性，實現了吸氣式高超聲速飛行器的自增益穩定飛行控制。