基于聲場模信號特征和多項式擬合的聲速剖面反演技術研究

劉福臣， 姬托， 張巧力

(1.聲納技術重點實驗室， 浙江 杭州 310023； 2.杭州應用聲學研究所， 浙江 杭州 310023)

0 引言

自1976年Bucker[1]提出匹配場處理(MFP)方法以來，與匹配場和聲學建模有關研究在過去的幾十年里得到了迅速發展。在海洋聲場數值計算[2-3]基礎上，MFP可以通過模型與數據的匹配來反演環境參數或估計目標距離，并選擇合適的算法。另外，失配是制約匹配場性能的主要問題，包括環境失配和系統失配，環境失配包括聲速剖面、海底特性不確定，系統失配包括陣列傾斜、水聽器相移等。

在海洋環境獲取技術中，聲速剖面主要利用多個測量聲速矩陣的正交分解，得到特征值所對應的特征向量，再將其表示為經驗正交函數(EOF)的形式獲得。沈遠海等[4]已經驗證了在淺海環境下利用EOF表示聲速剖面的可行性。張鎮邁等[5]也嘗試了在深海中聲速剖面的EOF表示并實現了聲速梯度的反演。Li等[6]利用基于水平線陣的匹配場反演方法來反演聲速剖面并通過南海海域數據進行了驗證。何利等[7]和Yu等[8]詳細研究了匹配場反演聲速剖面的可行性。何利等其他學者[9-20]對不同海域的聲速剖面反演展開研究。然而在不熟悉聲速剖面情況下，反演聲速剖面則較為困難，同時由于溫鹽深儀(CTD)/拋棄式溫深儀(XBT)等聲速剖面測量儀器的相關費用，水聲學面臨的一個挑戰是如何開發單傳感器的聲速剖面反演方法。

由于垂直陣反演面臨陣形失配的問題，在實際應用中難以準確實現參數反演，因為陣形帶來的失配遠比聲速參數失配要嚴重，同時在實際聲納設備中，沒有垂直孔徑的基陣可供參數反演，因此本文瞄準單水聽器開展參數反演的研究。

本文提出了一種基于模信號[5]和多項式擬合的聲速剖面反演方法，該方法采用多項式擬合聲速剖面，與EOF法不同，該算法具有低階多項式擬合的特點，通過理論推導和仿真分析，證明了該方法基于單水聽器接收的模信號進行聲速剖面反演的可行性，并通過海上試驗數據驗證了該方法的可行性。

1 基礎理論

1.1 模信號及其特性

依據簡正波理論，單水聽器的接收聲壓可簡寫為

(1)

(2)

(3)

式中：r為接收水聽器與目標間水平距離；z為接收深度；zs為目標深度；krm為第m號模態的本征值，ψm(z)為第m號簡正波的本征函數；ρ為海水密度；H為海洋深度；M為模態數目；f為頻率；S(f)為聲源頻譜。

定義第m號模信號Hm(r,z,f)頻域表達式為

(4)

相應的時域表達式為

(5)

在時域中，接收信號源自源信號s(t)與一系列模信號的卷積：

(6)

圖1(a)為Munk剖面，圖1(b)為深海傳輸函數，該函數可清楚地分為兩部分：第1部分(t=39.8 s)是海洋折射模信號簇；第2部分(t=41.5 s)是來自海底和表面反射的模信號簇。

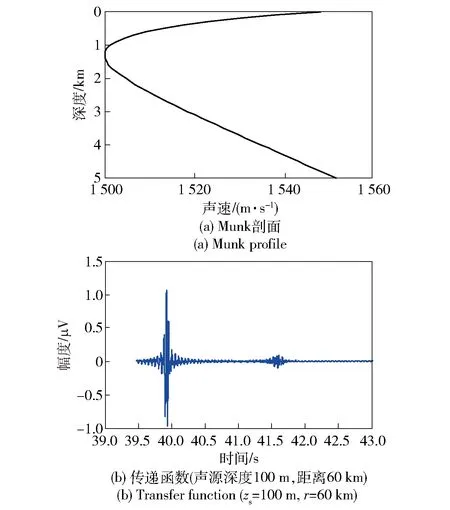
圖1 深海聲速剖面和模信號Fig.1 Deep sea sound velocity profile and mode signal

1.2 基于多項式擬合的聲速剖面表示方法

采用n階多項式擬合聲速剖面c(z)表示為

(7)

式中：

(8)

c(n)(0)為c(z)的n階導數。

典型深海聲速剖面如Munk，其具有完整的公式化表示：

(9)

式中：

(10)

利用多項式進行Munk聲速剖面的擬合，驗證聲速剖面近似表達的可行性，則聲速可以表示為

(11)

式中：b1=1 466.835；b2=0.017；b3=11.055；k0=2；k1=-0.001 5.

進行n+1階Taylor展開，表示為

c(z)≈b1+b3ek0+(b2+b3k1ek0)z+

(12)

多項式擬合系數分別為

(13)

圖2給出了不同擬合階數n的聲速剖面。由圖2可以得出結論：1)對于典型Munk聲速剖面，擬合階數越高，全海深聲速剖面的貼合程度越高；2)不同擬合階數對淺表層的聲速剖面的貼合程度都非常高，雖然低階展開無法實現全海深的聲速剖面準確擬合，但5階情況下對聲道軸以淺的水文擬合比較好。當允許一定的誤差存在時，采用較低的階數是可以進行聲速剖面擬合的。

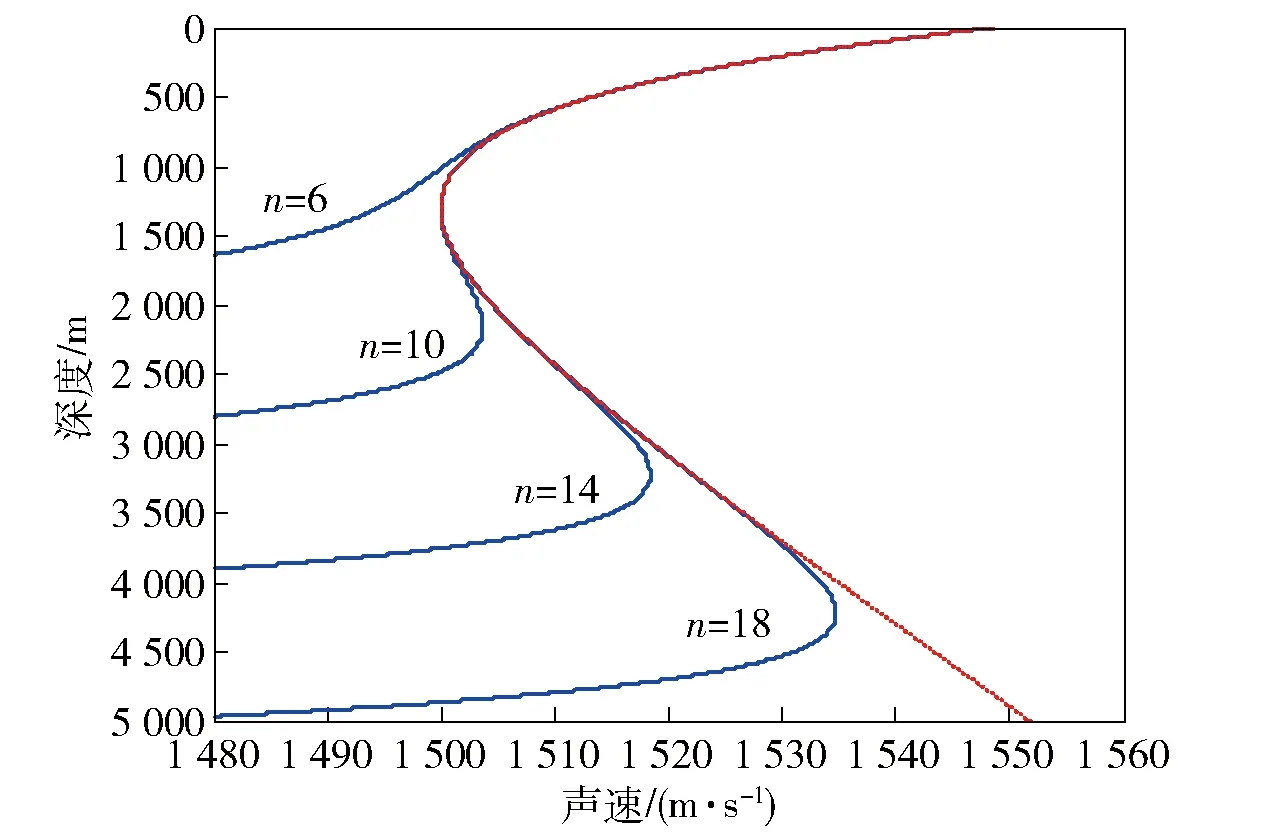
圖2 不同擬合階數下聲速剖面對比曲線Fig.2 Contrast diagram of fitting sound speed profile using different coefficients

圖3(a)給出了2 000 m海深的情況，分別采用3階、4階和5階多項式擬合，其中：3階擬合聲速剖面平均誤差為0.58 m/s、均方根誤差為0.68 m/s；4階擬合聲速剖面平均誤差為0.11 m/s、均方根誤差為0.13 m/s；5階擬合聲速剖面平均誤差為0.02 m/s、均方根誤差為0.02 m/s.

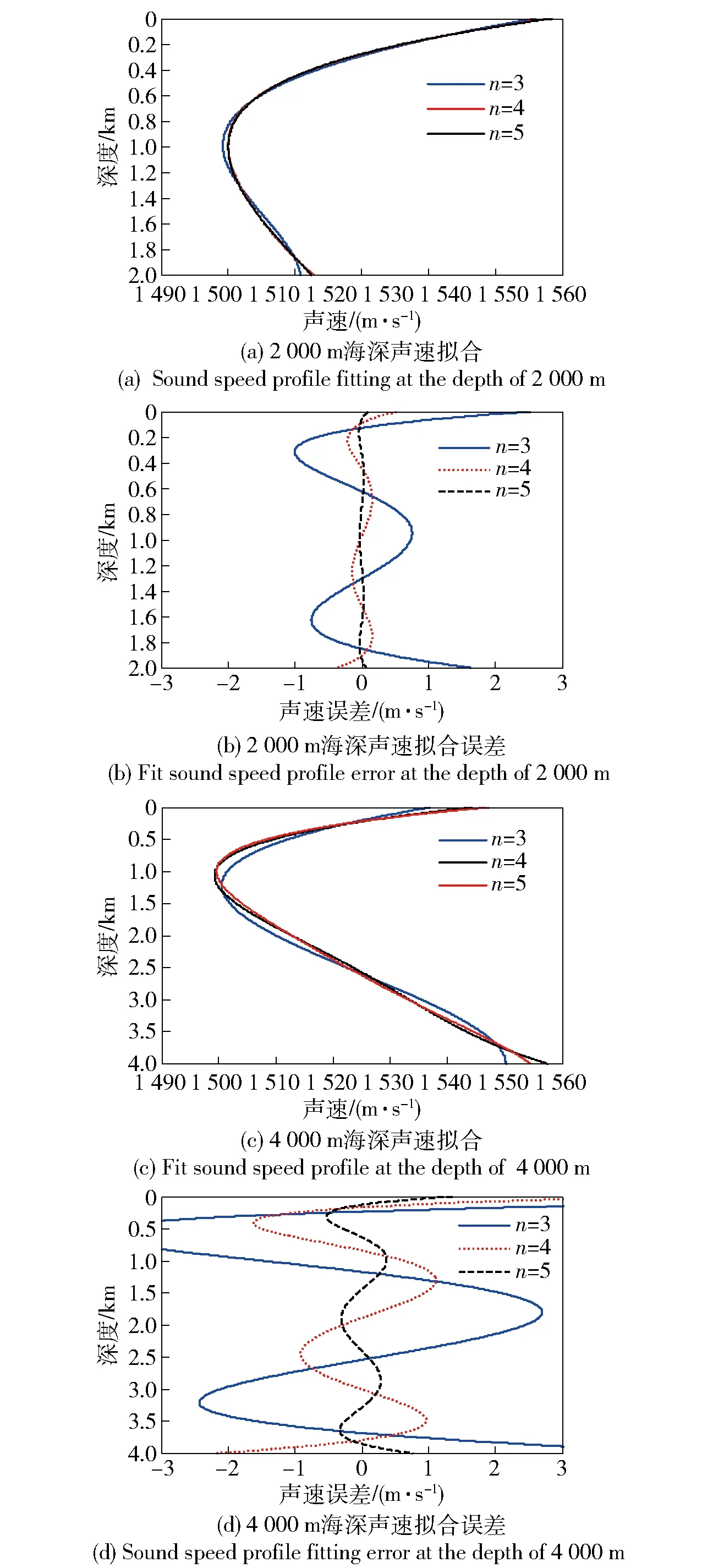
圖3 不同擬合階數下聲速剖面對比曲線Fig.3 Contrast diagram of fitting sound speed profile using different orders

圖3(c)給出了4 000 m海深的情況，分別采用3階、4階和5階多項式擬合，其中：3階擬合聲速剖面平均誤差為2.1 m/s、均方根誤差為2.6 m/s；4階擬合聲速剖面平均誤差為0.77 m/s、均方根誤差為0.93 m/s；5階擬合聲速剖面平均誤差為0.23 m/s、均方根誤差為0.29 m/s.

通過以上理論和仿真分析，對于實際聲速剖面，在反演誤差一定情況下，可以采用低階多項式擬合表層聲速剖面，在下面行文中，分析兩種聲速剖面，其中：2 000 m海深聲速剖面采用4階多項式擬合，平均誤差可控制在0.12 m/s以內；4 000 m海深聲速剖面采用5階多項式擬合，平均誤差可控制在0.3 m/s以內。這對于聲場預報和實際應用基本可以滿足需要。

為驗證多項式擬合性能，選取南海與西太平洋典型海區聲速剖面進行分析。查海洋環境數據庫，海區1為臺灣以東海域(東經125.8° 北緯23.3°)、海區2為臺灣以東海域(東經123°，北緯23°)、海區3為南海北部(東經16° 北緯20°)聲速剖面分別如圖4～圖7所示(測量聲速剖面為歷年平均值)。圖4(a)、圖5(a)、圖6(a)和圖7(a)分別給出了測量聲速剖面與反演聲速剖面的對比結果，圖4(b)、圖5(b)、圖6(b)和圖7(b)分別給出了測量聲速剖面與反演聲速剖面的反演誤差，聲速剖面反演平均誤差分別為0.4 m/s、0.38 m/s、0.3 m/s和0.4 m/s，證明利用多項式進行深遠海聲速剖面表征是可行的。由數據庫查詢的聲速剖面為歷史平均值，由于測量數據本身存在誤差，尤其是0～500 m深度區間。

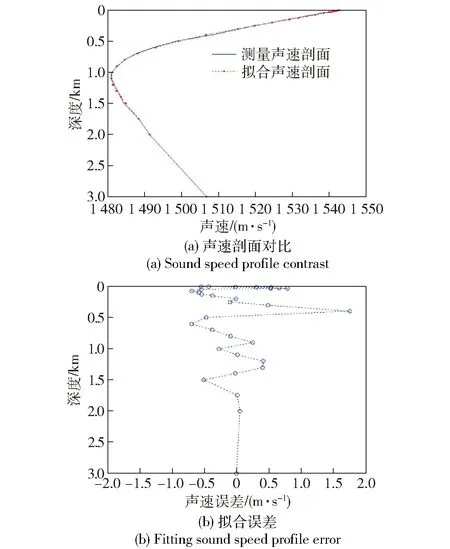
圖4 海區1(6月份)測量聲速剖面與擬合聲速剖面對比Fig.4 Comparison of sound speed profile measured in sea area 1 (June) with fit sound speed profile

圖5 海區2(6月份)測量聲速剖面與擬合聲速剖面對比Fig.5 Comparison of sound speed profile measured in sea area 2 (June) with fit sound speed profile

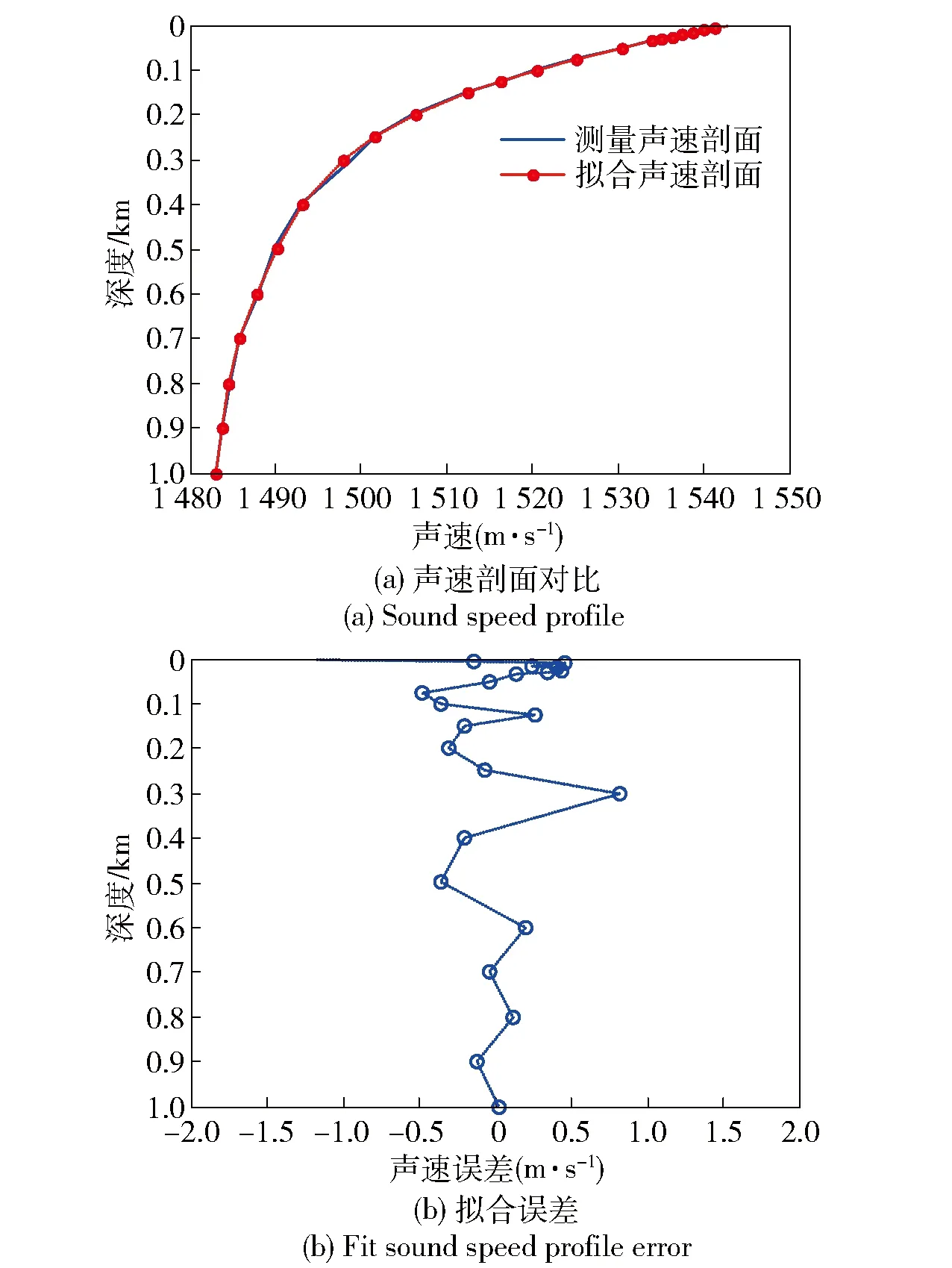
圖6 海區3(6月份)測量聲速剖面與擬合聲速剖面對比Fig.6 Comparison of sound speed profile measured in sea area 3 (June) with fit sound speed profile

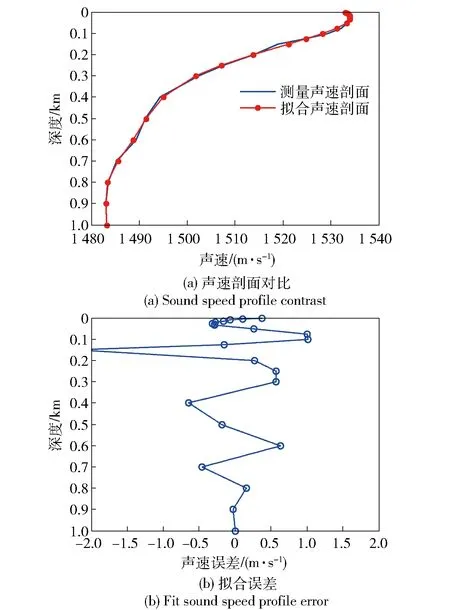
圖7 海區3(12月份)測量聲速剖面與擬合聲速剖面對比Fig.7 Comparison of sound speed profile measured in sea area 3 (December) with fit sound speed profile

鑒于深海聲速剖面在較大深度處基本穩定，同時也為了減小測量誤差和反演時間，因此本文在深度大于2 000 m時采用歷史平均值處理，主要反演深度2 000 m以下的部分。

2 反演算法

深海中的垂直列陣(VLA)如圖8所示，海底由基底層組成，其中cb、ρb、αb分別表示基底層的聲速、密度和吸收系數。因此，當確定海底參數時，所需的反演參數包括系數向量。

圖8 接收垂直線陣與反演參數Fig.8 Received VLA and Inversion parameters

接收垂直陣的第k個單元在時域和頻域可以表示為p(r,zk,t)與P(r,zk,f)，垂直數據向量B可以用(14)式表示：

(14)

在反演算法中，拷貝信號Pe(r,zk,f)是通過簡正波模型得到的。在這里，拷貝垂直向量P可以表示為

(15)

Bartlett匹配處理器如(16)式所示：

(16)

式中：fl為下限頻段；fh為上限頻段。

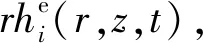
拷貝模信號與測量模信號匹配同樣采用Bartlett匹配處理器處理，如(17)式所示：

(17)

遺傳算法(GA)采用數學仿真軟件MATLAB GA工具箱中基于全局搜索參數空間的交叉啟發式函數，該處理器具有多徑壓縮能力，適用于高信噪比條件。

3 仿真分析

以Munk聲速剖面為參考，開展不同條件下的聲速剖面反演，仿真分析的思路：1)首先進行垂直陣條件下聲速剖面反演可行性分析；2)接著進行基于單水聽器接收的模信號聲速剖面反演；3)再論證在非海面海底傳播模式的聲速剖面反演可行性。在下面仿真中，多項式擬合系數均采用5階來處理，反演參數是采用參數空間遍歷進行的，同時結合參數的合理性。在選取參數時，依據聲速剖面的合理性進行選擇，如最后一項對應聲速的常數項部分，選擇從1 460～1 560 m/s的區間內選擇。

在實際反演處理中，對深海聲速剖面在大深度上相對穩定，因此在處理時采取2 000 m以淺采用多項式擬合(為獲取聲道軸深度，擴大了擬合的深度范圍)，2 000 m以深進行采用歷時平均值處理。

3.1 利用垂直陣的聲速剖面反演

表1給出了利用垂直陣的聲速剖面反演仿真參數，其中：海區深度為4 000 m，聲速剖面為典型Munk剖面，聲道軸深度為1 300 m；目標距離為30 km，深度100 m，接收基陣均勻布放在100～200 m之間，陣元間距為7.5 m；處理頻段采用20～40 Hz.

表1 利用垂直陣的聲速剖面反演仿真參數

本例調用KRAKEN模型的次數為20 800次，GA在代價函數值小于6.93×10-8時停止搜索，計算時間為120 min. 表2給出了搜索結果。圖9和圖10給出了聲速剖面反演結果，擬合聲速剖面與仿真剖面吻合，聲道軸深度相同，在全海深聲速剖面平均反演誤差為0.14 m/s.

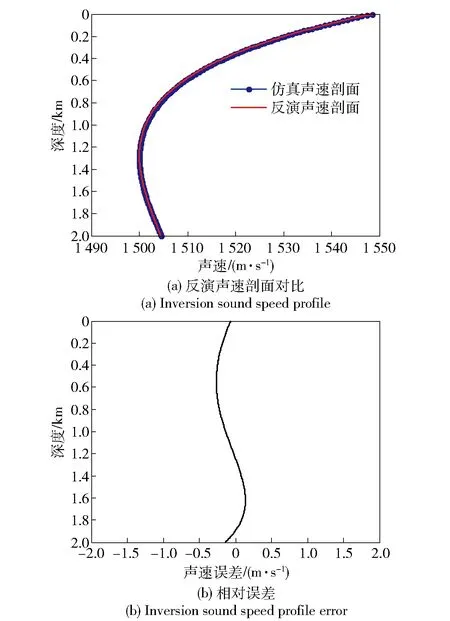
圖9 仿真剖面與反演聲速剖面比較Fig.9 Comparison of real sound speed profile and inversion sound speed profile

但在實際海洋波導中，基于垂直陣的參數反演存在缺陷在于，大深度垂直陣陣形難以測量，這會給參數反演帶來較大誤差；實際應用中，聲納平臺沒有較大垂直孔徑，難以滿足垂直陣反演的要求。因此，基于單平臺、單節點的聲速剖面反演更具實際意義和工程應用前景。

表2 多項式擬合參數反演結果

3.2 利用單水聽器模信號的聲速剖面反演

研究結果表明：垂直陣陣形失配對反演影響遠比環境參數失配要嚴重，因此本文瞄準單水聽器開展參數反演的研究。下面給出利用單水聽器接收的模信號進行聲速剖面反演的仿真結果。

表3給出了利用單水聽器模信號的聲速剖面反演仿真參數，其中：海區深度為2 000 m，目標距離為60 km，深度100 m，水聽器接收深度在100 m之間；處理頻段采用20～40 Hz.

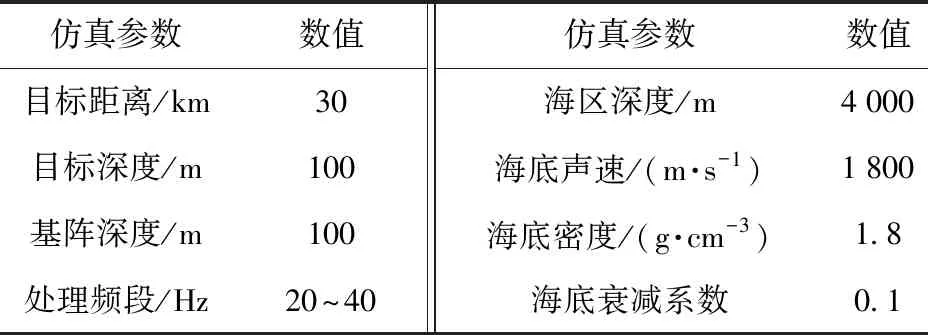
表3 利用模信號的聲速剖面反演仿真參數

本例調用KRAKEN模型的次數為20 800次，GA在代價函數值小于5.479×10-8時停止搜索，計算時間為120 min. 表4給出了搜索結果。圖11和圖12給出了聲剖面反演結果，擬合聲速剖面與仿真剖面吻合，聲道軸深度相同，全海深聲速剖面平均反演誤差在0.15 m/s以下，算法性能與垂直陣反演接近，證明基于單水聽器模信號反演是可行的。

表4 多項式擬合參數反演結果

圖11 仿真剖面與反演聲速剖面比較Fig.11 Comparison of real and inversion sound speed profiles

圖12 利用模信號的聲速剖面反演參數收斂圖Fig.12 Inversion parameters

3.3 利用單水聽器非海面海底反射模信號的聲速剖面反演

當海底參數未知，基于單水聽器反演不會得到好的結果，因為存在海底海面反射模式，是受海底參數(包括海底起伏、海底分層結構及其各層聲學參數)影響的。只有利用非海面海底反射(SRBR)模信號才能減小環境參數失配帶來的影響。

表5給出了利用垂直陣的聲速剖面反演仿真參數，其中：海區深度為4 000 m，目標距離為30 km，深度100 m，水聽器接收深度在100 m；處理頻段采用20～40 Hz. 這里采用非SRBR模信號進行反演，如圖11所示。

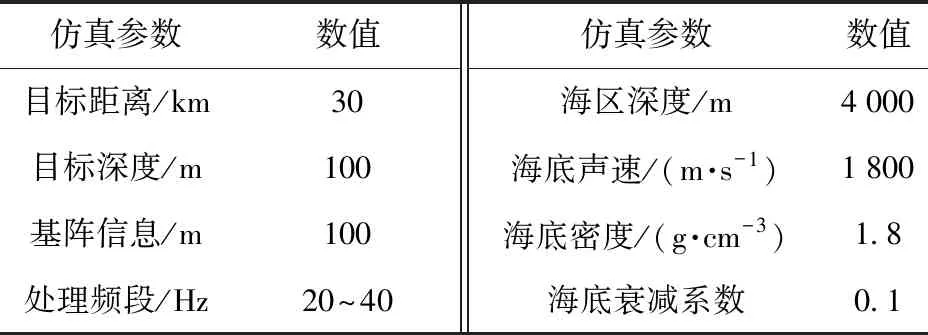
表5 利用非SRBR模信號的聲速剖面反演仿真參數

結果如表6所示，本例調用KRAKEN模型的次數為20 000次， GA在代價函數值小于6.997×10-8時停止搜索，計算時間為120 min. 圖13和圖14給出了聲速剖面反演結果，擬合聲速剖面與仿真剖面吻合，平均誤差0.16 m/s，基本可以滿足環境參數測量的需求。圖15為基于簡正波模型計算得到的非SRBR信號。這一仿真結果表明，利用非SRBR模信號反演可以減小海底參數失配的影響，提升在海底參數未知條件下的反演性能。

表6 多項式擬合參數反演結果

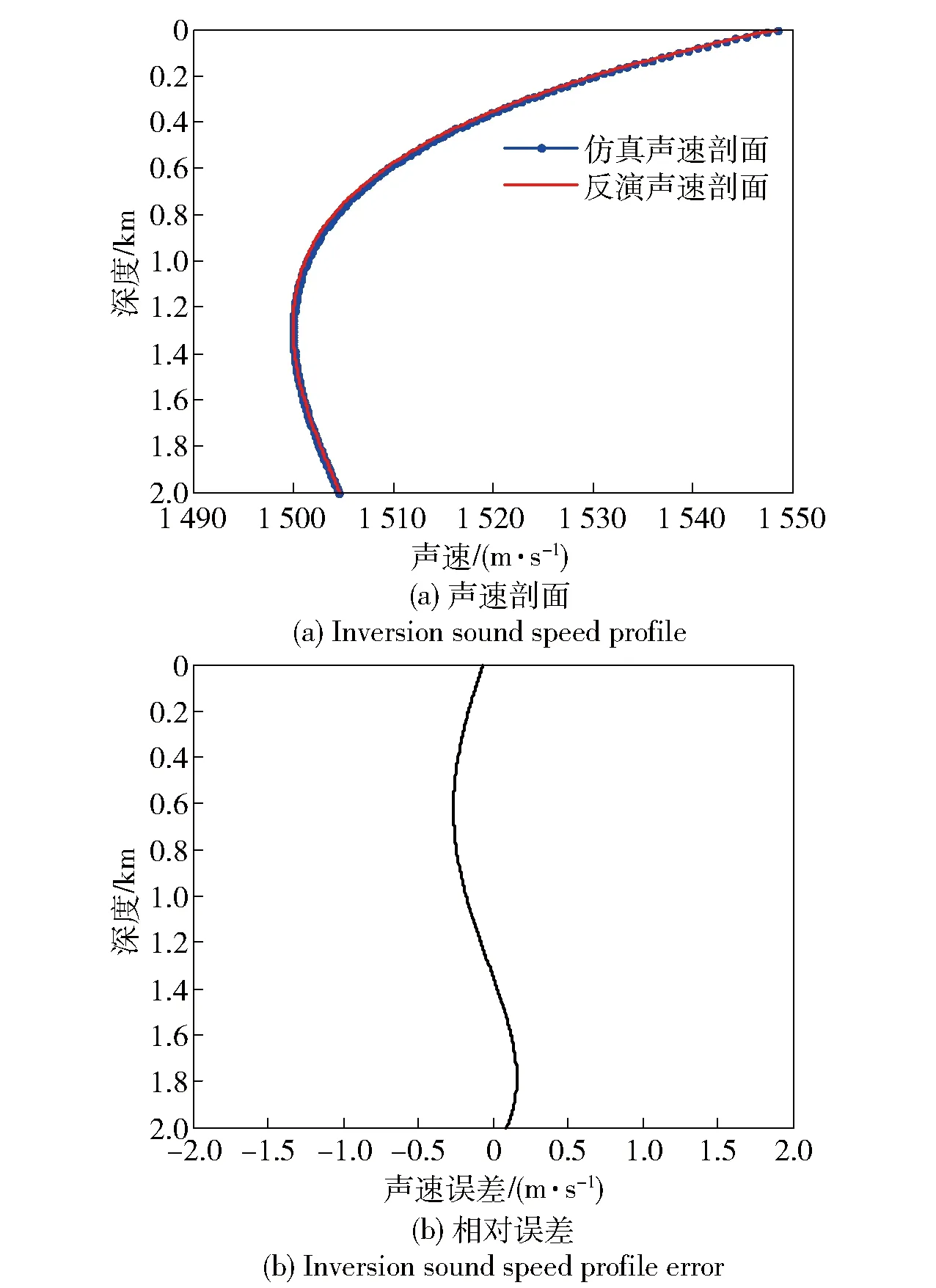
圖13 仿真剖面與反演聲速剖面比較Fig.13 Comparison of real and inversion sound speed profiles

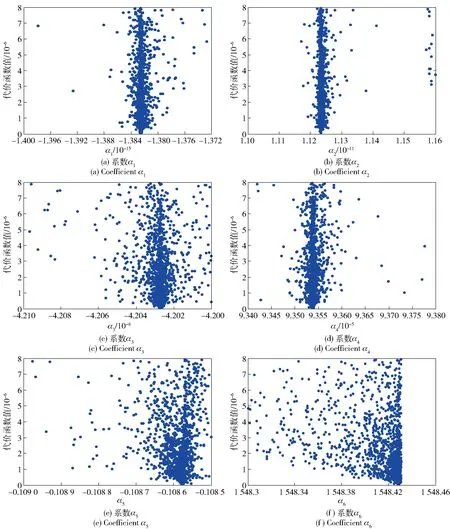
圖14 利用非SRBR模信號的聲速剖面反演收斂圖Fig.14 Convergent graphs of sound speed profile inversion parameters based on non-SRBR mode signal

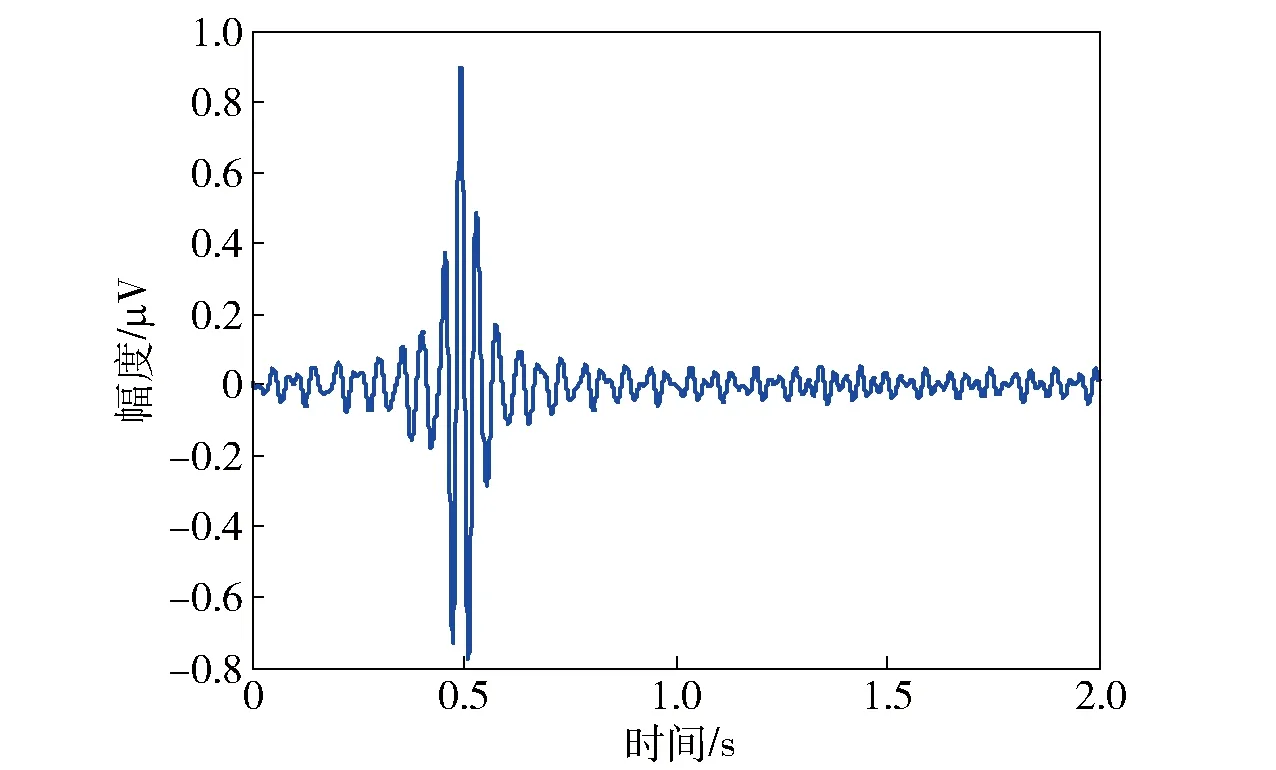
圖15 非SRBR模信號Fig.15 Non-SRBR mode signal

前面對垂直陣、單水器和非SRBR單水聽器3種情況下反演參數進行對比分析，在相同環境條件下(海深均為4 000 m，聲道軸深度為1 300 m，目標距離為30 km、深度為100 m，處理頻段均為20～40 Hz)，在海底參數、陣形或陣元未知(不失配時)、3種方法基本相當，獲得聲速剖面與實際吻合，證明本文提出方法是可行的。而且該算法優勢在于：1)當陣形失配時，利用垂直陣反演將無法獲得好的結果；2)當海底參數未知，基于單水聽器反演將不會得到好的結果，因為存在海底海面反射模式，是受海底參數影響的；3)當海底參數未知，利用非SRBR信號的聲速剖面反演仿真仍然能得到好的結果。下面利用海試數據進行驗證。

4 海試數據處理

2018年5月進行了深海基礎性試驗，試驗區域海深約為3 750 m，聲速剖面如圖16所示。表面聲速接近1 542 m/s，海底聲速約為1 520.7 m/s，試驗測線海深最大起伏約為950 m.

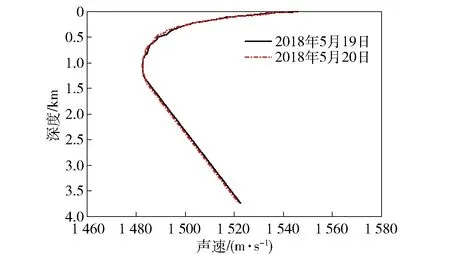
圖16 測量聲速剖面Fig.16 Sound speed profiles on sea areas

圖17為試驗海域的水深分布，自容式潛標布放在圖17原點位置處，海深約為2 800 m，最遠投彈點海深為3 750 m.

圖17 深水聲傳播測線海深分布Fig.17 Water depth of sea test route

對接收深度為30 m和40 m的水聽器接收信號進行分析，驗證該方法的反演性能，爆炸聲源距離為48.9 km、深度為200 m，如圖18和圖19所示。

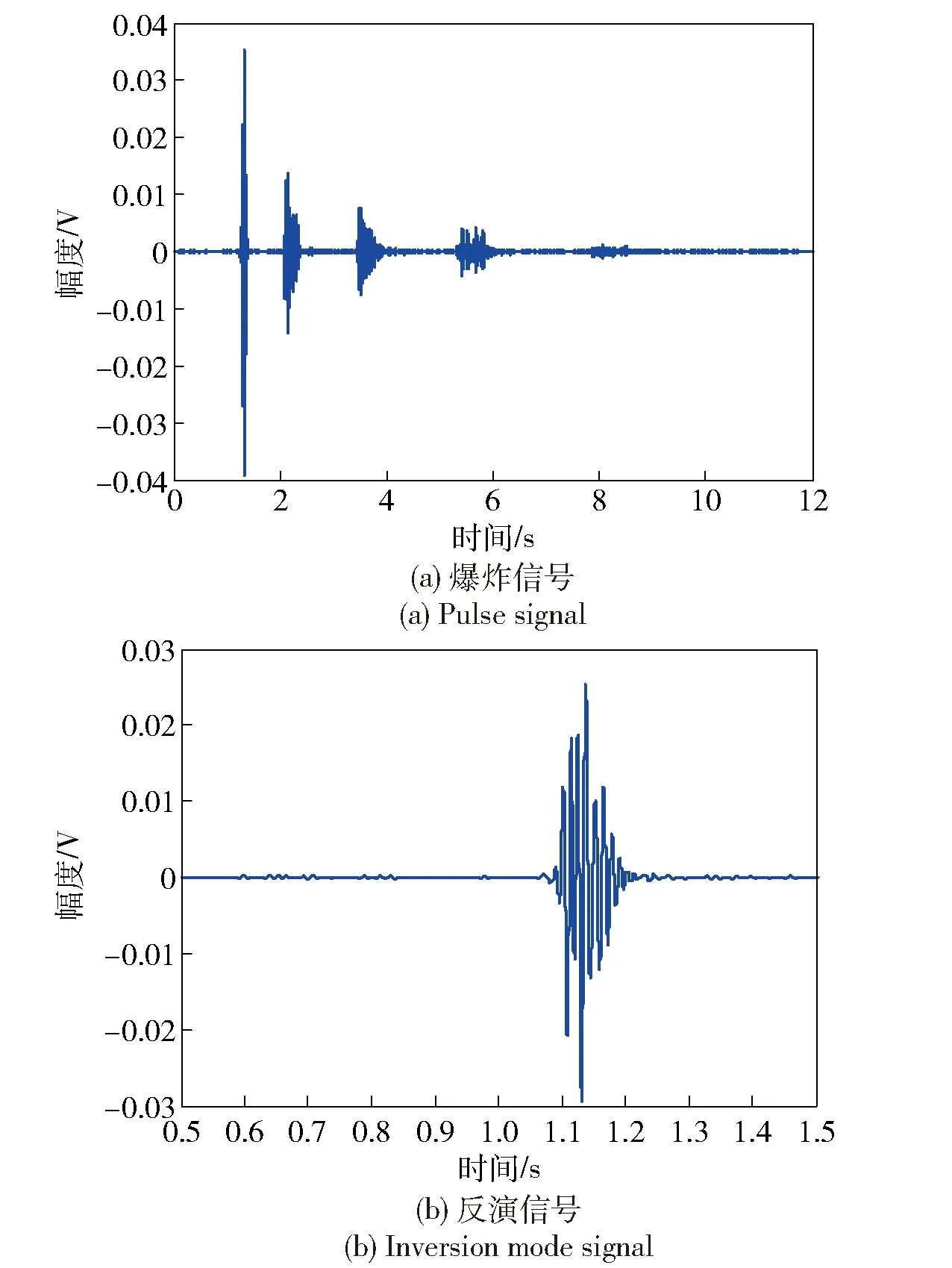
圖18 接收信號(距離48.9 km、深度300 m)Fig.18 Signal received by the hydrophone (distance: 48.9 km, and depth: 300 m)

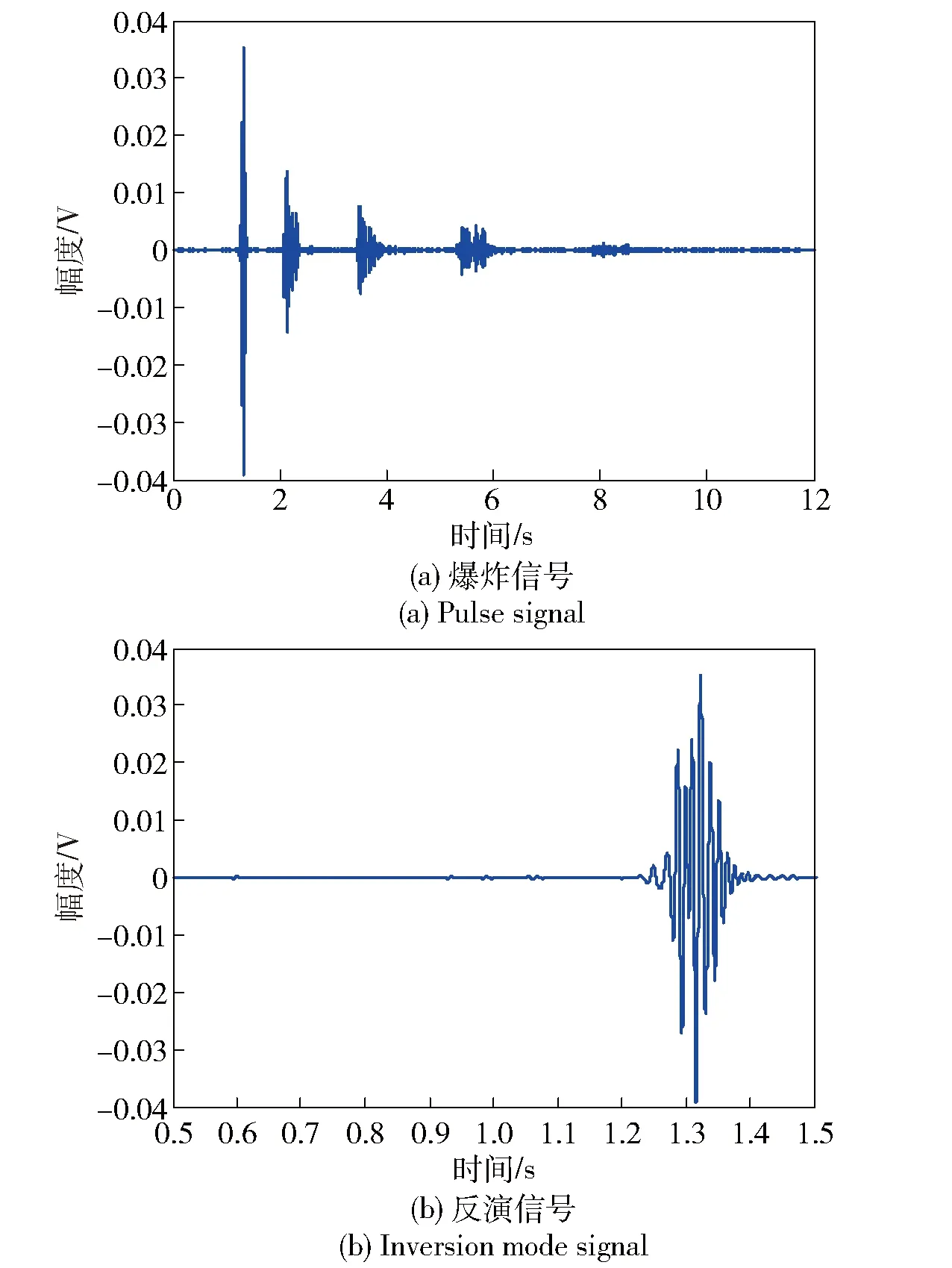
圖19 接收信號(距離48.9 km、深度400 m)Fig.19 Signal received by the hydrophone (distance: 48.9 km, and depth: 400 m)

圖18(a)是水聽器接收深度為300 m的脈沖信號，圖18(b)是選擇的反演信號，它主要由非SRBR模式信號組成。圖19(a)是水聽器接收深度為400 m的脈沖信號，圖19(b)是選擇的反演信號，它同樣由非SRBR模式信號組成。

表7列出了每個參數的收斂值。圖20給出了聲速剖面反演的結果。由表7可以看出，反演的聲速剖面與實測的聲速剖面是一致的，聲道軸的深度是一致的。

表7 多項式擬合參數反演結果

圖20 測量聲速剖面和反演聲速剖面對比Fig.20 Comparison of measured and inversion sound speed profiles

圖21為不同深度的聲速剖面誤差。該數據反演結果表明：反演聲速剖面在100 m以淺誤差較大，在0～100 m深度范圍內反演誤差接近1.14 m/s；在100～2 000 m深度反演誤差誤差小于0.2 m/s. 由于非SRBR模式信號對海底參數不敏感，這種方法可以解決海底參數未知情況下的聲速剖面反演問題。

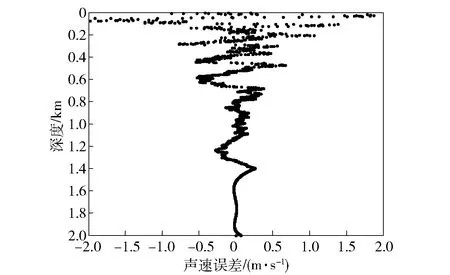
圖21 測量聲速剖面和反演聲速剖面誤差Fig.21 Inversion sound speed profile error

5 結論

本文介紹了模信號的概念和深海分布特性，通過理論分析和仿真分析，證明低階多項式擬合可用于深海聲速剖面的表征；在此基礎上，提出了利用基于聲場模信號特征和多項式擬合的聲速剖面反演技術研究，并對比分析了基于垂直陣、單水聽器、非SRBR信號的反演性能；最后利用海試數據驗證了反演算法的可行性。主要結論如下：

1) 采用5階多項式擬合可以實現對2 000 m以淺的聲速剖面較精確的表征。

2) 提出的反演算法適用于垂直陣、單水聽器。海底參數與陣形已知條件下反演性能基本相當，但單水聽器數據的反演更具應用前景。

3) 當海底參數未知條件下，采用單水聽器接收的非SRBR模信號可以實現對共軛深度以下聲速剖面的準確反演，適用陌生海域的海洋環境信息獲取。