La-W共摻雜對AgSnO2觸頭材料熱性能影響的仿真分析

陳 令，王景芹，朱艷彩，張廣智，包志周

(1.河北工業大學,省部共建電工裝備可靠性與智能化國家重點實驗室,天津 300130；2.上海良信電器股份有限公司,上海 200137；3.浙江人民電器有限公司,溫州 325604)

1 引 言

電接觸材料在高低壓電器通斷電流中起著關鍵作用，其性能的好壞直接關系到電器開關的壽命長短[1]。電觸頭材料可分為固定接觸、可分接觸、滑動接觸和滾動接觸，通常低壓電器由Ag(包括AgNi(0.5))、AgNi、AgCuO、AgCdO、AgSnO2、AgSnO2In2O3、AgZnO等制成[2]，電接觸材料廣泛應用于各類電器產品中，如繼電器、接觸器、空氣開關、汽車電器(照明、啟動電機等用電負荷)及家用電器等。所以，電接觸材料的可靠性為保證電器能夠正常工作至關重要。因此，尋找各方面性能良好的電觸頭材料是當下亟待解決的問題。AgSnO2觸頭材料由于具有耐電弧侵蝕、抗熔焊等優越性能而在電接觸材料中得到普遍應用[3]。但AgSnO2作為電接觸材料在實際應用中會出現溫度升高、接觸電阻變大等影響其導電、導熱性能的情況，許多研究證明通過摻雜金屬或非金屬元素來改善其導電性及導熱性[4]。康慧玲等[5]采用稀有金屬共摻雜AgSnO2觸頭材料方法進行研究，發現共摻雜后的材料禁帶寬度減小，載流子由價帶激發到導帶所需的能量減少，使SnO2的導電性有較大提升。本文也從中得到啟發，通過單摻、共摻雜AgSnO2觸頭材料方式對晶胞結構進行優化計算，對比、分析摻雜后對材料導熱行為的影響。

本文運用基于密度泛函理論[6](Density Functional Theory，DFT)的第一性原理方法對純SnO2、La單摻雜SnO2及La-W共摻雜SnO2觸頭材料的各物理參數進行計算[7-9]。計算得到聲子譜曲線，通過其判斷出摻雜后晶體結構的穩定性；通過聲子態密度及分波態密度分析摻雜后各原子之間的相互作用，判斷晶體結構的振動情況；利用獲得的熱力學參數對熱容的影響，分析摻雜對晶體熱導率的影響。利用第一性原理的計算方法，可以有效地在眾多摻雜配比中篩選出表現較優的摻雜結構，縮小尋找范圍，為找到較好的觸點材料提供了指導。進而通過找到的合適摻雜配比進行觸點材料制備及測量，方便試驗方面的研究，有效的節省了人力、物力、財力。

2 理論模型和計算方法

2.1 晶體模型

本文采用的晶體模型是1×2×3的SnO2超晶胞，其晶格常數為a=b=0.4737 nm，c=0.3186 nm，α=β=γ=90o。其模型中包含12個Sn原子，24個O原子。La原子及W原子的摻雜模型則通過La及W原子替換晶胞中的Sn原子，摻雜濃度保持為16.67%。其摻雜前后晶體結構模型如圖1所示。

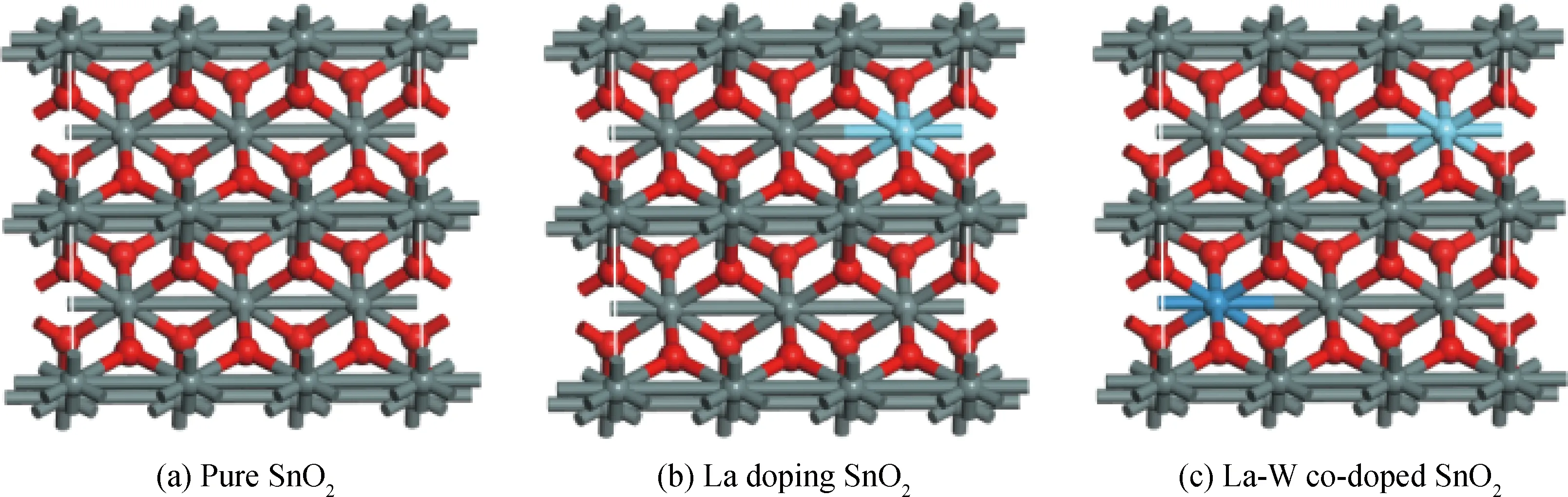
圖1 SnO2及其摻雜模型Fig.1 Models of SnO2 and SnO2 doping

2.2 計算方法

本文晶胞的優化、聲子譜的計算是在Materials Studio軟件中的CASTEP模塊進行的，基于密度泛函理論(DFT)的倒空間 Norm-conserving 贗勢方法,交換關聯函數采用廣義梯度近似方法(GGA+PW91)，GGA近似方法克服了描述真實體系在密度變化劇烈的情況下的缺陷，提高了交換相關能的計算結果，從而提高了密度泛函方法計算的精度。價電子和芯態電子的相互作用采用投影綴加平面波(PAW)方法來描述[10-11]。布里淵區采用5×5×8的 Monkorst-Park方案，平面波截斷能選擇750 eV，優化均采用BFGS算法，原子間相互作用收斂標準規定為0.3 eV/nm，內應力最大值設定為 0.05 GPa。

首先，通過Materials Studio軟件中的CASTEP模塊對構建好的模型進行優化計算，得到較為穩定的結構。然后，對優化后的模型進行聲子譜、聲子態密度及分波態密度和熱力學參數(德拜溫度、熵、焓及自由能)的計算。

3 計算結果與分析

3.1 SnO2晶體振動性質

3.1.1 聲子譜分析

聲子譜描述的是晶體內部各個振動元的振動情況，是衡量晶體穩定性的重要指標。對于任何一種晶體結構，晶格動力學要求所有簡正振動模的頻率都是一定限度的實數值，對于布里淵區的任一格波，其聲子頻率不能為虛數，即滿足聲子穩定性[12]。當體系中出現虛頻聲子，表明該體系中系統能量不能處于最小值，將被更低能量的晶體結構所取代，這就促使晶體結構的對稱性遭到破壞，最終系統會發生結構相變，則表明該體系是不穩定的[13]。

在同一摻雜濃度16.67%的條件下。圖2(a)～(c)所示依次為根據計算模擬得到的SnO2、La單摻及La-W共摻的聲子色散曲線。由圖2(a)、(c)可以看出聲子色散曲線都在0 Thz以上，說明純SnO2、La-W共摻情況下未出現虛頻聲子，即這兩種情況下體系是穩定的。而圖2(b)出現了一條聲子曲線在0 Thz以下，出現了虛頻聲子，即表明該體系中系統能量不能處于最小值,從而使晶體結構的對稱性遭到破壞而發生結構相變，則說明La單摻情況下體系是不穩定的。由此可以看出，共摻La-W的晶體比單摻La元素的晶體穩定性要好，其中W元素的摻雜對體系的穩定性起到了關鍵的作用。通過對比圖2(a～c)可以看到，未摻雜體系獲得的聲子譜曲線相比其它摻雜情況的曲線較為粗糙，這與超晶胞的模型大小有關，當模型較小時，會出現較為尖銳的聲子色散。為避免出現此種情況，建模時需要建立較大模型。

圖2 聲子色散圖Fig.2 The diagram of phonon dispersion

3.1.2 聲子態密度及分波態密度分析

圖3給出了計算所得的SnO2(a)、La單摻雜(b)、及La-W共摻雜(c)的聲子態密度與分波態密度圖。經分析發現La單摻雜(圖3(b))情況下振動模式在-5～0 THz頻段存在頻譜，而圖3(a)、(c)所示的頻譜都在0 THz以上，結合上文其出現的虛頻聲子，進一步說明La原子單摻情況下體系是不穩定的，原因是La原子摻雜后，會產生頻段小于0 THz的振動模式，從而使晶體的聲子色散出現虛頻。

La-W共摻雜后，由圖3(c)可以看出，La原子的振動模式全部出現在大于0 THz的頻段，說明經W原子混合摻雜后可有效的改善La原子的振動情況。而La原子與W原子的分態密度比較接近，均分布在0～10 THz低頻段之間，高頻段幾乎為零，由此說明La-W原子之間具有較強的耦合作用。

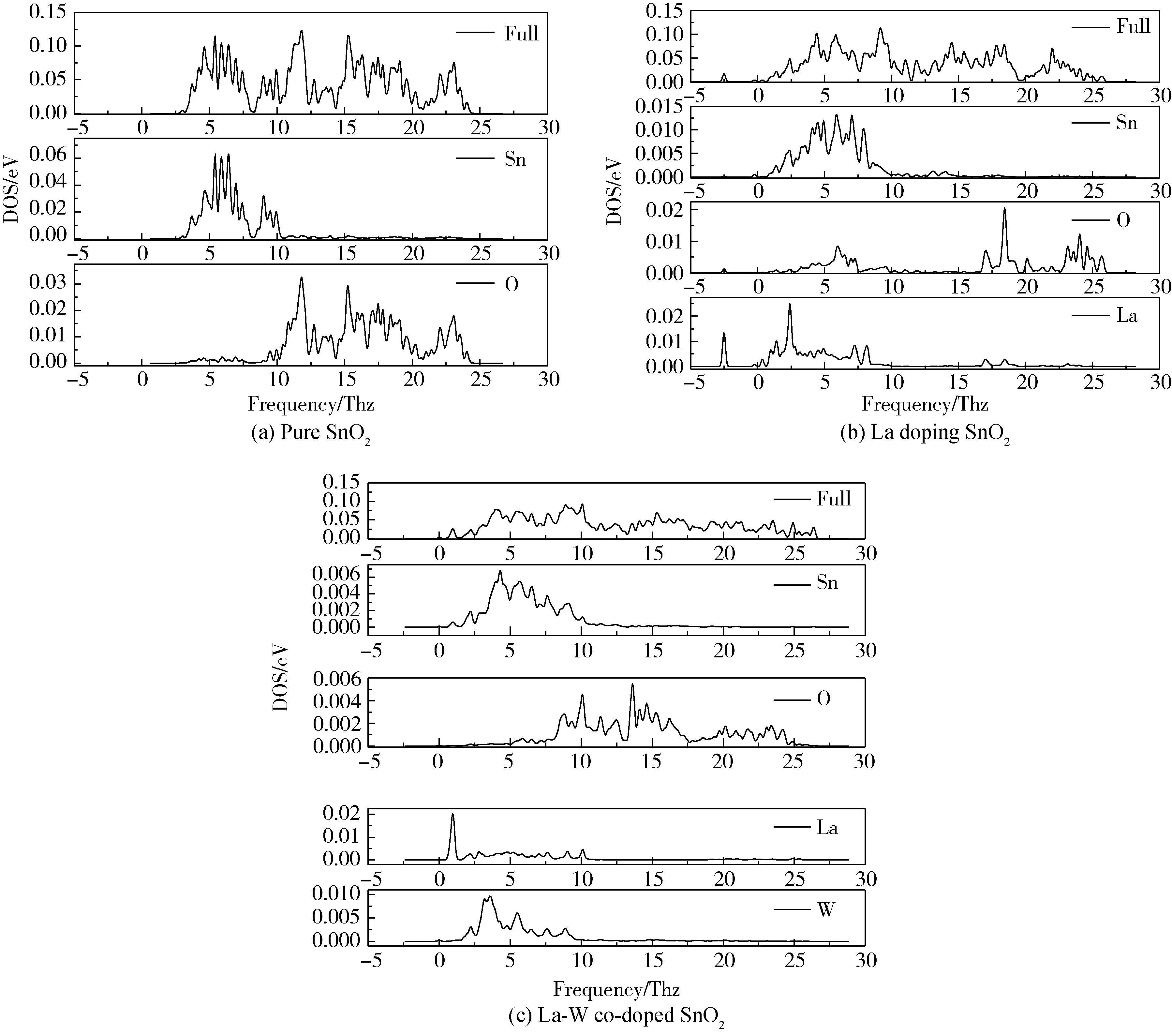
圖3 晶體總態密度和分波態密度圖Fig.3 The diagram of total state density and partial wave state density of crystal

3.2 SnO2晶體熱力學性質分析

利用計算得到的聲子譜可以得到聲子的熵、自由能以及聲子的焓，三者是反映材料熱力學性能的重要參數，如圖4所示。

其中，熵值反映了外界條件變化導致晶體生存、發展和進化活動的根本機制，在物理系統中是分子運動狀態的參量，它表征分子運動的混亂程度，反映了原子運動的劇烈程度[14]。由圖4(a)可以看出，摻雜前后體系的熵都隨溫度升高而升高且共摻雜后體系的熵上升更快，說明摻雜La-W元素后可以有效提高體系的熵值，即提高了各原子的運動活性，使分子運動能夠從低度有序走向高度有序，從而促使體系由一個穩定狀態走向另一個穩定狀態。

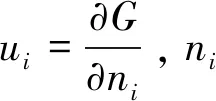
聲子的焓描述的是體系在等壓條件下，晶體吸收的熱量[17]。分析圖4(c)發現，共摻雜后體系的焓曲線較未摻雜體系的焓曲線陡峭，說明共摻雜后的體系吸收的熱量更多。

結合上述三個熱力學參數分析得到：同等條件下，La-W元素共摻雜下與不摻雜體系相比，熵值升高，提高了各原子的運動活性；自由能下降，為晶體相變提供了足夠的驅動力；焓值升高，為體系提供了足夠的熱量。可以判斷AgSnO2觸頭材料在惡劣環境下受到損害后，摻雜La-W元素后晶體的恢復能力要優于未摻雜晶體的恢復能力。

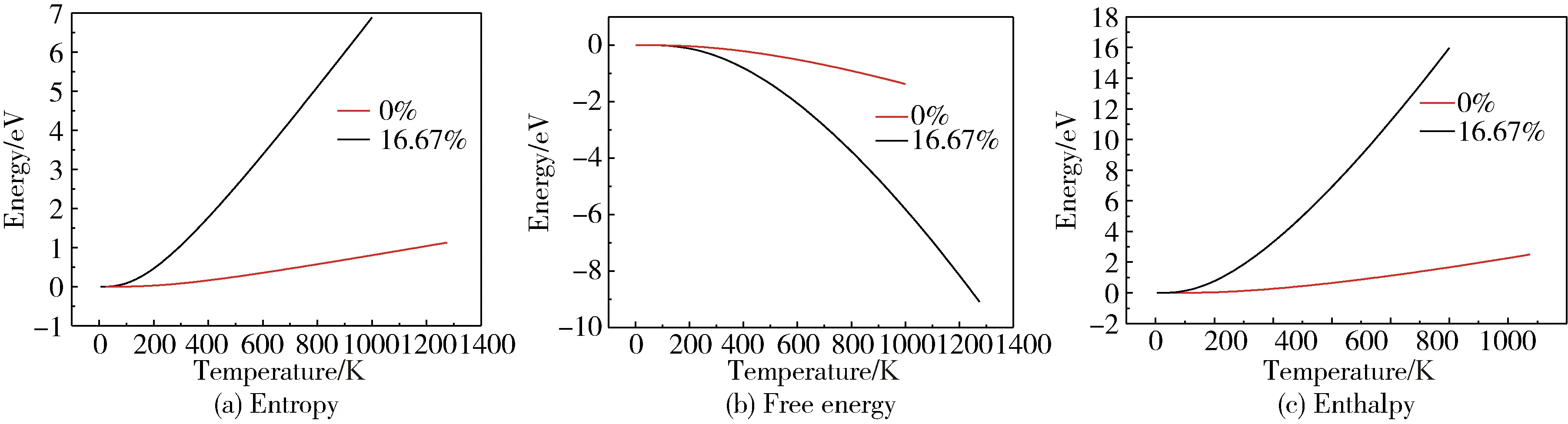
圖4 SnO2晶體熱力學函數隨溫度變化曲線Fig.4 The thermodynamic function of SnO2 crystal varies with temperature

3.3 熱容分析

由聲子分波態密度計算了摻雜前后SnO2晶體熱容隨溫度變化的曲線，如圖5所示。最初，隨著溫度的上升，參與運動的分子逐漸增多，熱容隨之增加；當溫度升高到一定程度時，參與運動的分子趨于飽和，則熱容便不會隨溫度升高而增加，漸趨于定值。由此，可以說明熱容的變化取決于分子的運動狀態，即與參與運動的分子數量有關。

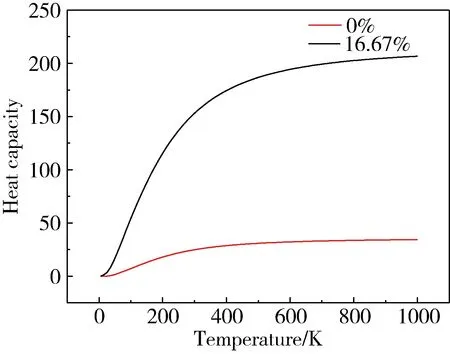
圖5 聲子熱容與溫度的關系Fig.5 The relation between phonon heat capacity and temperature

由圖5可以看到，La-W摻雜后體系的熱容明顯大于未摻雜體系的熱容，而針對摻雜前后晶體熱容的差異分析可知，La-W元素的摻雜，使得晶體中分子的活性增強，即參與運動的分子增多。同時結合本文晶體的熵值曲線，也進一步說明了La-W元素的摻雜極大的激活了分子的運動活性，進而增大了晶體的熱容。

4 結 論

本文通過Materils Studio軟件中的CASTEP模塊對純SnO2及摻雜La元素的晶體進行了熱學性能的計算，得到以下結論：

(1)通過分析聲子譜曲線，共摻雜La-W元素體系的聲子譜未出現虛頻，單摻La元素體系的聲子譜出現了虛頻。說明共摻La-W的晶體比單摻La元素的晶體穩定性要好，其中W元素的摻雜對體系的穩定性起到了關鍵的作用。

(2)通過分析聲子態密度及分波態密度，La原子單摻雜后，會產生頻段小于0 THz的振動模式。而La-W共摻雜后，La原子的振動模式全部出現在大于0 THz的頻段，說明W原子混合摻雜后可有效的改善La原子的振動情況且兩種元素間具有較強的耦合作用。

(3)通過SnO2晶體熱力學性質的分析，共摻雜后體系的熵、自由能以及焓的曲線變得陡峭，為AgSnO2觸頭材料在惡劣環境下受到損害后恢復到原狀提供了有利條件，即提高了晶體的恢復能力。

(4)摻雜后晶體的熱容明顯大于未摻雜晶體的熱容，說明了La-W元素的摻雜極大地激活了分子的運動活性，進而增大了晶體的熱容。