基于“示以思維”的數學實驗常態教學策略

【摘 要】在數學實驗形態學范疇內“示以思維”包括信息關聯型、系統補償型和遷移可逆型，涉及數學思考、數學判斷和實現問題解決等核心素養的形態思維。通過對數學實驗“示以思維”的研究，讓常態數學實驗從“教理解”轉向“教智慧”，從“學以致用”轉向“用以致學”，進而發展學生的“關鍵能力”。

【關鍵詞】“示以思維”;數學實驗;數學思考策略;常態教學研究

【中圖分類號】G633.6? 【文獻標志碼】A? 【文章編號】1005-6009（2019）83-0014-03

【作者簡介】朱桂鳳，江蘇省連云港市鳳凰學校（江蘇連云港，222000）教師，高級教師，江蘇省特級教師。

對數學實驗教學法而言，“示以思維”就是在研究數學問題時，將邏輯思考的過程建立體系，并將此思維過程可視化。“示以思維”能幫助學生構建某一類的知識體系，這就要求教師在實驗教學時要“示以思維”地教，為學生鋪墊思維。這樣的常態化實施數學實驗，有助于學生抽象、推理和建模思想的發展。學生的知識技能、思想方法、活動經驗、能力素養及其結構體系的構造與建設，需要“示以思維”“授以思考”，方能讓數學實驗從“教理解”轉向“教智慧”，從“學以致用”轉向“用以致學”。

本文主要以《數學實驗手冊》中的實驗項目為思考對象，建構“示以思維”視角下的數學實驗常態化實施教學策略。

一、在經歷中催生數學思考

這里的“經歷”是指在特定的數學活動中，讓學生獲得一些感性認識。這種“感性認識”是在抽象中獲得的、在經歷中形成的。數學抽象是數學學習的三大能力（抽象、推理和建模）之一，是初中段學生畏懼數學的一個重要原因，也體現出張奠宙教授說的數學“冰冷與火熱”的特征（數學概念、原理、方法本身很冰冷，但背后的數學思考極其火熱）。對初中生而言，他們處于從形象思維向抽象思維過渡的階段，需要一個幫助其思維發展的載體。數學實驗是一種數學活動，具有彌補數學抽象思維短板的功能，有助于學生在“經歷中”，自覺地生發數學思考。

更具體地來說，數學實驗是發展學生抽象能力的間接載體，有助于學生在直觀中抽象，在抽象中進行信息關聯，形成“知其然和知其所以然”的思維方式。傳統的數學課堂立足于“知其然，不知其所以然”的“告訴概念+重復訓練”的思維方式，不利于學生將知識上升到能力素養層面，經不起實踐的檢驗。而數學實驗課堂關注“是什么、為什么和怎么樣”，其優勢就在于能將“知識經驗”轉化為“思想方法”。因此，常態化實施數學實驗意義重大。

在南京大學教授呂林海看來，數學抽象從背景上看具有客觀性，從產生上看具有能動性，從內容上看具有特殊性，從方法上看具有構造性，從過程上看具有發展性。這就要求我們在實施常態數學實驗時，一是關注數學抽象的客觀性，創設問題情境，關聯思維;二是關注數學抽象的能動性，采用“做數學”的思維方式;三是關注數學抽象的過程性，在經歷數學中體驗數學的多元思考，進而發展數學“核心素養”。

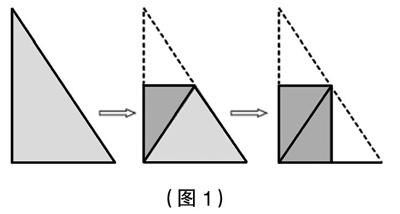
例如，我們將直角三角形紙片按圖1所示的方法折疊成這樣的兩個矩形稱為“組合矩形”。在下定義的基礎上，首先讓學生剪一個銳角三角形紙片，折成“組合矩形”，說明理由，并由此說明三角形的中位線與第三邊之間的數量關系;其次是在方格紙上，讓學生畫出頂點都在格點上的三角形，使該三角形折成的“組合矩形”為正方形，并通過折疊加以驗證;最后是讓學生基于“特殊—一般”思想，思考非特殊的四邊形滿足什么條件時能折成“組合矩形”，畫出這樣的四邊形并進行折疊驗證。

上述“定義組合矩形→折組合矩形→折組合正方形→探討折成組合矩形條件”的過程，涵蓋了“特殊→一般→特殊”、“折→剪→畫→判斷”以及“直角三角形→銳角三角形→非特殊四邊形”的過程，這樣的實驗經歷，能讓學生既獲得知識又獲得方法。

二、在體驗中形成數學判斷

在數學實驗常態化實施中，“實驗體驗”是參與特定的數學活動，主動認識或驗證對象，獲得真實經驗的過程。在這一過程中，一方面數學實驗作為“領悟課程”，需要通過“動手做”還原推理的思維本真，落實“怎樣到達那里”;另一方面數學實驗作為“運作課程”，需要“活動數學”，將靜態的概念轉化為動態的數學思考，建立系統概念。正如《義務教育數學課程標準（2011年版）》（以下簡稱“2011年版課標”）強調的那樣，學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程。

基于這一認識，需要做好三個層面的系統補償工作，讓學生在信息體驗中提升數學判斷能力。一是運用信息技術操作畫圖，體驗數學目標;二是說數學，展示自己的數學思維過程;三是概括推理，發展數學判斷力。

2011年版課標指出，教師應當努力開發制作簡單實用的學具和教具，有條件的學校可以建立“數學實驗室”供學生使用，培養他們的實踐能力和創新精神。比如，在研究“中點四邊形”這一實驗時，可以讓學生在“希沃環境”（一種教學軟件平臺）下畫圖，獲得對中點四邊形的認識與理解，建構系統關聯的學具思維。具體操作順序如下。

首先是讓學生在“希沃環境”下，畫出一個四邊形的“中點四邊形”，然后下定義。其次是讓學生畫出特殊四邊形的“中點四邊形”，猜想平行四邊形、矩形、菱形、正方形的“中點四邊形”形狀，說理并折紙驗證。最后是讓學生任意畫一個四邊形的“中點四邊形”，探尋該四邊形的對角線滿足什么條件時，其中點四邊形是矩形、菱形和正方形，并驗證。

如果說“軟件畫圖→形象定義”是由體驗到形成判斷，那么“畫出→猜想→驗證→說理”是由做數學到說數學，而“畫圖→判斷→推理→概括”則體現了學習的系統性。這樣的實驗形態，一方面有助于學生形成概念體驗，另一方面能讓學生在體驗中獲得“示以思維”，并將“結構知識”轉化為“認知結構”，這就是數學實驗常態化實施的工具思維。

三、在探索中實現問題解決

數學實驗必須堅持“在實踐中”和“向實踐學習”的立場。數學實驗作為“經驗課程”，一方面需要實踐，落實行為探索目標;另一方面需要向實踐學習，讓學生在問題解決中獲得解決問題的能力。例如，在研究“特殊四邊形”概念時，讓學生任意畫一般三角形、等腰三角形、等邊三角形和等腰直角三角形，并分別畫出其繞頂點或直角頂點旋轉180°后的圖形，猜想并驗證四邊形的形狀。這種實踐的立場，有助于學生產生“問題意識”，形成問題能力，這就是向實踐學習的表現形式。

在南京大學鄭毓信教授看來，“問題”可以理解成“找出適當的行動以達到一個可見而不能立即可及的目標”。在數學實驗活動范疇，提出問題是人們創造性能力的一個重要內涵。因為解決問題也許是一個數學上或實驗上的一個技能，而提出新的問題、新的理論，從新的角度去看舊的問題，卻需要創造性的想象力。

2011年版課標指出，要重視學生已有的經驗，使學生體驗從實際背景中抽象出數學問題、構建數學模型、尋求結果、解決問題的過程。這里的“情境→抽象→建模→解決問題”是數學實驗常態化實施的基本形態，是知識、發展逆向思考的一種“示以思維”和實踐舉措。這就要求教師設置的“問題解決”教學具有探索性、可逆性以及潛在的遷移性和創新性。讓學生在探索中獲得舉一反三和觸類旁通的能力，這就是數學實驗常態化實施的不可替代性。

在數學實驗常態發展的過程中，探索性是發現和提出問題的創新基礎;可逆性就是讓學生在“做”和“思考”的過程中，形成獨立思考、逆向思考和學會思考的能力，進而實現問題的雙向回流，這是數學創新的核心;遷移性就是讓學生通過歸納概括得到猜想和規律，并加以證明，這是創新方法。可以說任何一個實驗都是以“問題→建模→解模和使用模型”的思維程序呈現的，一方面能讓學生獲得創新能力，另一方面能讓學生形成可逆遷移，落實經驗課程發展學生數學素養的功能。■

【參考文獻】

[1]呂立杰，李剛.核心素養在學校課程轉化的層級分析[J].課程·教材·教法，2016（11）：50-56.

[2]邱冬，王光明.平面幾何教學的新視角——“示以思維”——基于章建躍先生對“研究三角形”的過程分析[J].數學通報，2018（8）：27-30.

[3]李昌官.數學抽象及其教學[J].數學教育學報，2017（4）：61-64.

[4]嚴虹.基于能力要求的初中數學課程國際比較研究[J].教學與管理，2018（30）：80-83.

[5]鄭毓信.“問題意識”與數學教師的專業成長[J].數學教育學報，2017（5）：1-5，92.