淺水中低速小半徑回轉船舶水動力數值研究*

王小龍 鄒早建 夏 立 劉敬賢

(上海交通大學船舶海洋與建筑工程學院1) 上海 200240) (上海交通大學海洋工程國家重點實驗室2) 上海 200240) (武漢理工大學航運學院3) 武漢 430063)

0 引 言

長期以來，關于船舶直航、斜航運動的研究遠多于關于船舶回轉運動的研究，然而，完整的操縱性預報離不開船舶回轉性能的預報.因此，準確預報船舶回轉性能依然需要投入更多的時間和精力.

由于船舶低速航行時間占整個生命周期的很小一部分，船舶的低速運動很容易被忽略，特別是港口附近的低速大漂角回轉運動.為提供預報港口操縱運動所需的基礎數據，Yumuro[1]使用Esso Osaka船模進行了一系列約束模試驗和螺旋槳敞水試驗等，并給出了各工況下船舶所受水動力的試驗結果.Yoshimura等[2]提出了一種簡單又通用、可適用于港口回轉操縱的數學模型，并通過與多種試驗結果對比，對該模型的預報精度進行了驗證.Wang等[3]以Esso Osaka為研究對象，對限制水域中船舶的回轉流場進行了模擬，并得到了船舶的相關受力.盧錦國等[4]應用基于RANS方法的數值方法，采用旋轉坐標系法，對潛艇的回轉性能進行了研究.Toxopeus等[5]也是基于該數值方法，分別使用商業和定制求解器對不同湍流模型、不同網格拓撲結構下的穩定回轉流場進行了數值模擬.Broglia等[6]通過求解非定常RANS方程研究了不同螺旋槳模型對船舶回轉預報的影響.Zhang等[7]也是基于數值方法對不同回轉半徑、不同漂角工況下的多種潛艇的回轉運動進行了研究.吳召華等[8]提出了體積力模型來表達螺旋槳的作用，并數值預報了回轉船舶的受力和力矩.Ortolanind等[9]研究了船舶在直航和回轉工況下螺旋槳槳軸的徑向受力.Dubbioso等[10]對全附體雙槳船的回轉能力進行了分析，并且還對比了單槳配置和雙槳配置船舶的回轉能力.Chen等[11]采用DES模型對不同漂角工況下、船舶的低速回轉運動進行了數值模擬，并提取了船舶運動過程中的受力及流動中的渦結構.

淺水中低航速船舶在不同漂角工況下的小半徑回轉運動常見于港灣、入海口等航行水域，該水域的環境復雜，船舶航行其中，操縱難度大，碰撞、觸礁、擱淺等事故發生風險也高，準確預報該水域不同航行工況下船舶的受力對于提高船舶航行安全意義重大.

1 控制方程

在描述船舶運動時，引入兩個右手坐標系，分別為大地坐標系O-XYZ和隨船坐標系o-xyz,見圖1.其中，大地坐標系的原點O設在船舶回轉運動的中心，O-XY設于無擾自由面上，Z軸垂直向上；隨船坐標系的原點o設于船舶重心位置，x軸指向船首，y軸指向右舷.

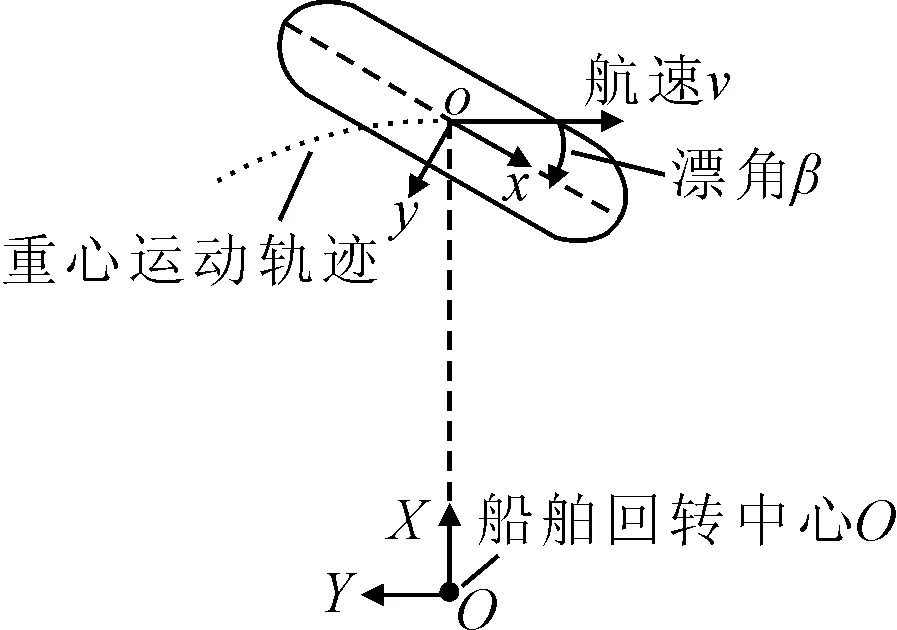
圖1 坐標系

控制方程為連續性方程和N-S方程，通過RANS方法求解時，流體控制方程為

(1)

(i=1,2,3)

(2)

式中：ui，uj和p均為時均量；ρ為流體質量密度；ν為流體運動學黏性系數；Tt為雷諾應力張量.

大地坐標系下船舶的回轉運動屬于非定常問題，對此，引入旋轉坐標系將大地坐標系下的非定常問題轉化成旋轉坐標系下的定常問題.旋轉坐標系為非慣性系，其原點位于回轉中心，并以船舶回轉的角速度進行旋轉，船舶此時相對于該系靜止，于是慣性系上的非定常問題就轉化為非慣性系下的定常問題.經坐標系轉化后的流體的控制方程為

(3)

(i=1,2,3)

(4)

式中：ω為旋轉角速度；r為旋轉參考系中位置矢量；δij為克羅內克符號.

2 計算設置

2.1 計算方法選擇

求解器選用STAR-CCM+，湍流模型采用k-ε模型，采用有限體積法對控制方程進行離散，采用標準格式對壓力項進行差分；速度、動量及湍流參量采用2階迎風差分格式進行離散；壓力與速度的耦合問題應用SIMPLE法處理；離散方程運用Gauss-Seidel法求解.

2.2 研究對象選擇

研究對象為Esso Osaka油船，其主尺度參數見表1，船體幾何見圖2.船舶運動過程中，所受橫向力為Fy，所受轉首力矩為MZ；fy，fz分別為量綱一的量的橫向力系數和轉首力矩系數，定義為

(5)

(6)

圖2 船體幾何形狀

2.3 計算域邊界及網格設置

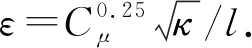
圖3 計算域

網格生成器選擇切割體網格，并執行棱柱層加密和自動表面修復，其中棱柱層延伸比為1.5，面網格延展比為1.3.第一層網格尺寸y=3.625×10-5m，95%以上船體表面y+值在5以內.為充分捕捉船體周圍流場，采用三重網格對船體附近進行加密，并在船體首尾處用更細的網格加密，見圖4.

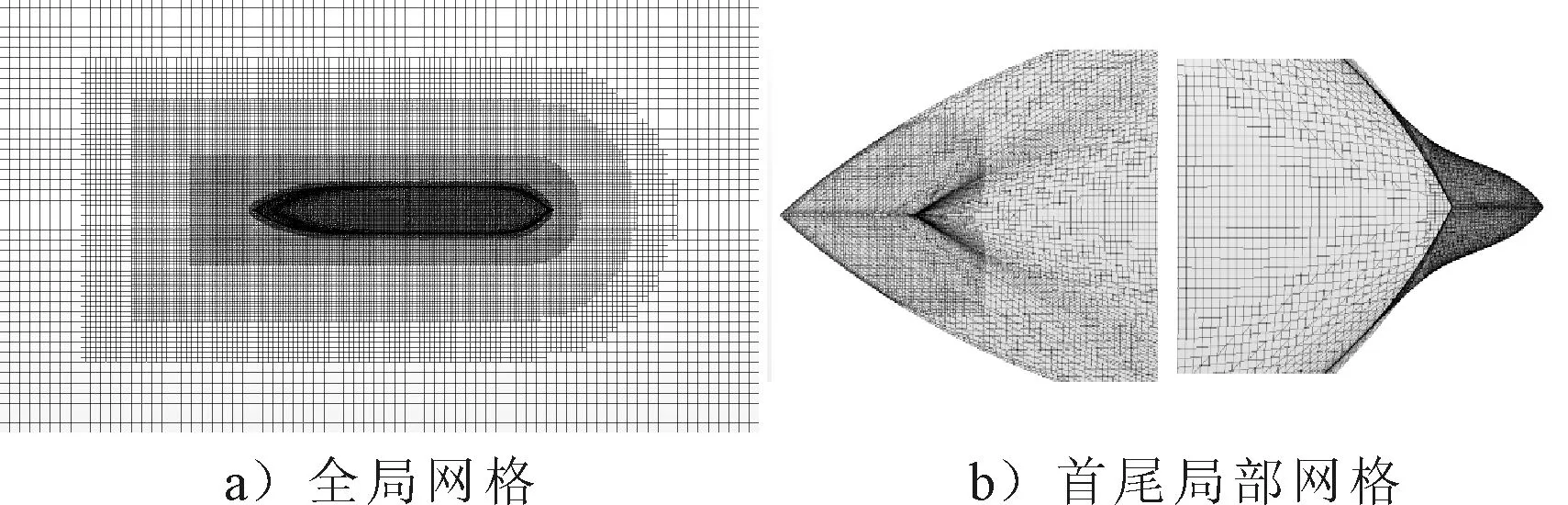
圖4 網格細節

3 方法驗證

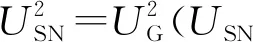
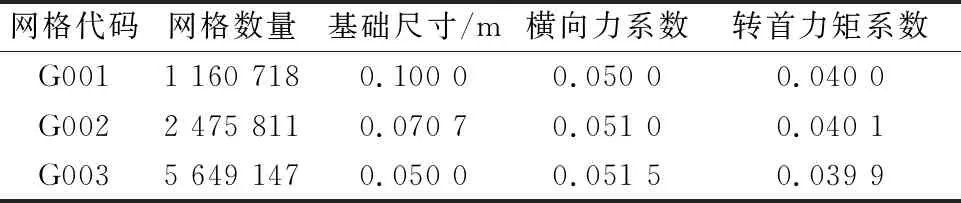
表2 網格信息及水動力計算結果

3.1 驗證

相鄰兩組網格對應的橫向力系數之差為εFG，有εFG21=SFG2-SFG1=0.001 0；εFG32=SFG3-SFG2=0.000 5.對應收斂率RFG為

根據文獻[16]所述，收斂狀況可分三種.

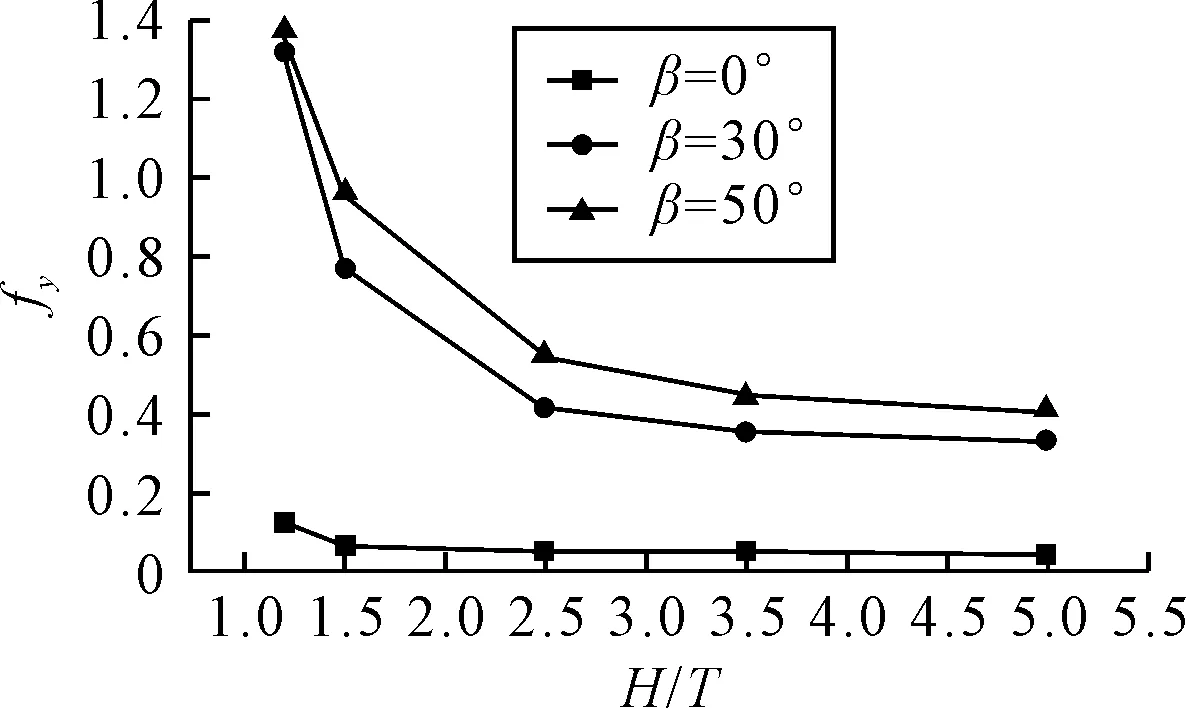
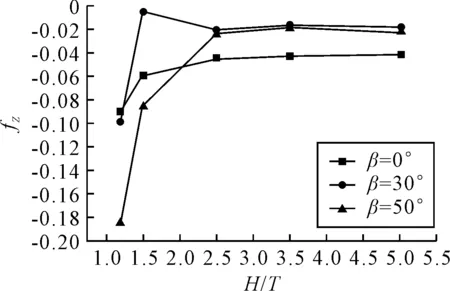
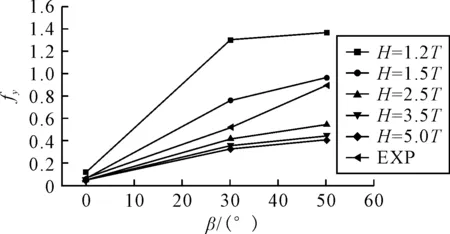
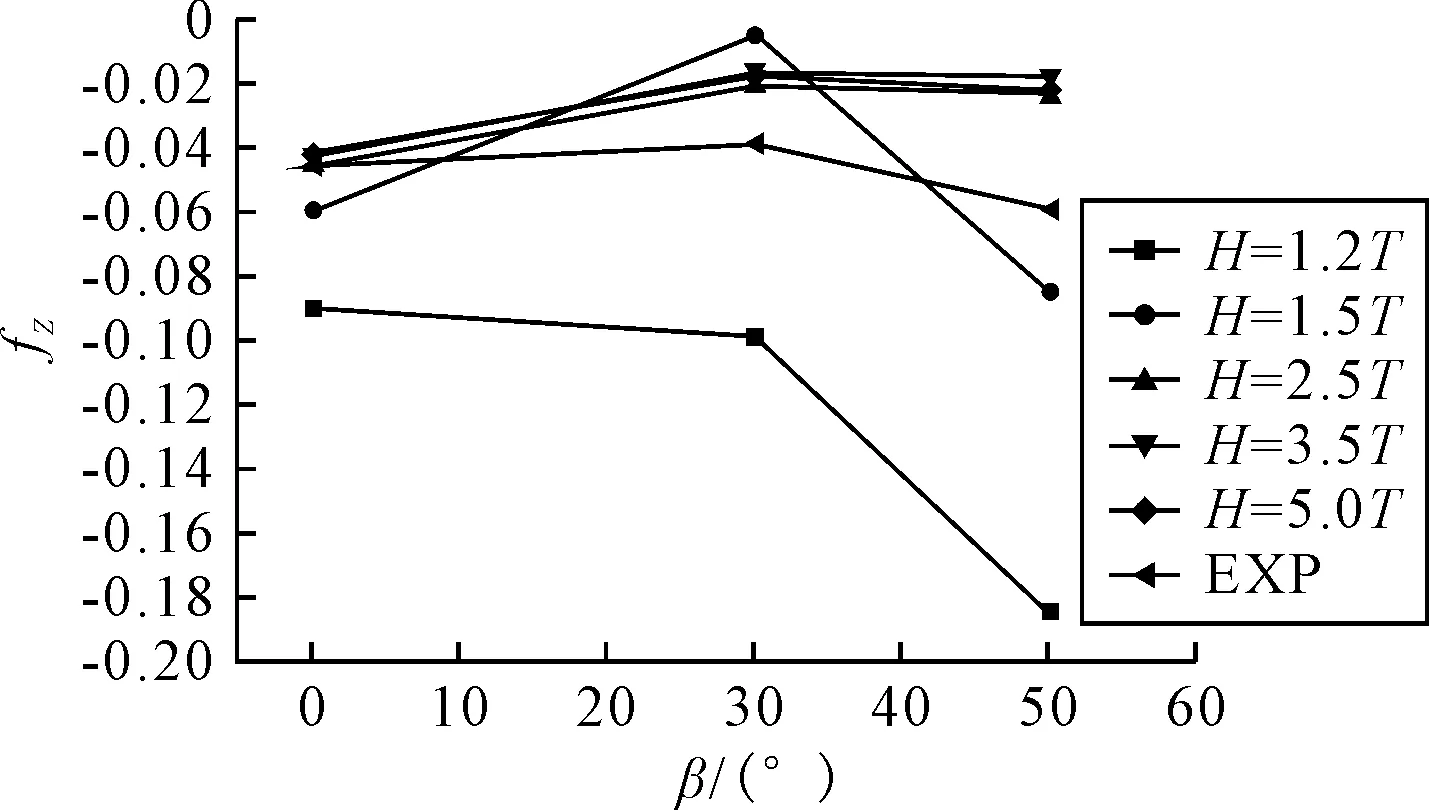
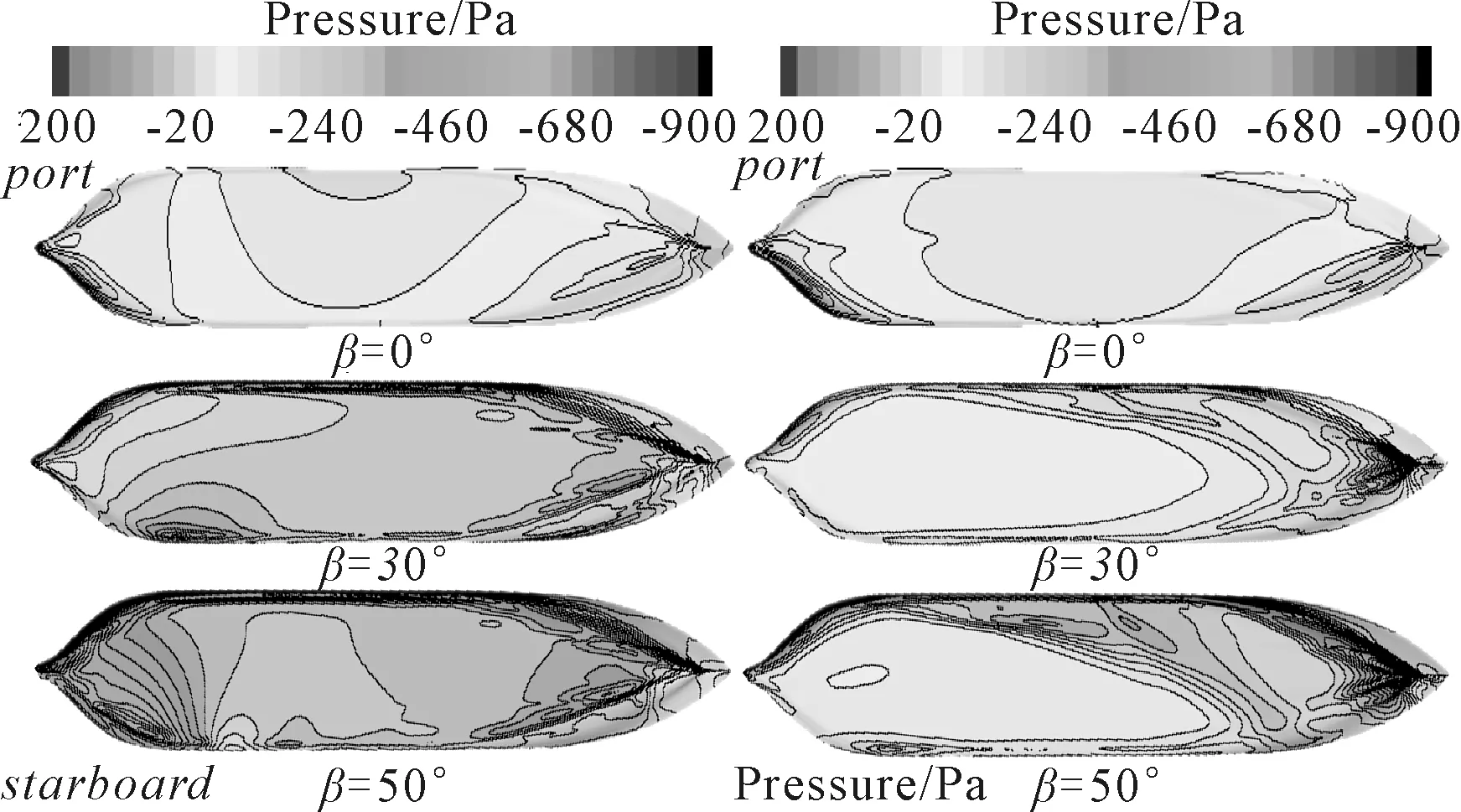
1) 0

2)RG<0，振蕩收斂，由振幅獲取誤差范圍；

3)RG>1，發散，無法估算誤差.

因RFG=2>1，所以橫向力系數誤差不確定度無法確定.

相鄰兩組網格對應的轉首力矩系數之差為εMG，有εMG21=SMG2-SMG1=0.000 1；εMG32=SMG3-SMG2=-0.000 2.對應收斂率RMG為

因為RMG=-0.5<0，所以轉首力矩系數只能根據振幅來估算：

3.2 確認

根據文獻[1]可知，橫向力系數的試驗值DF=0.071 0，轉首力矩系數的試驗值DM=0.045 9.文中數據讀取自文獻[1]，讀取過程本身會產生一定的誤差；同時不考慮自由面興波、岸壁效應及下蹲等物理現象，且試驗船模帶附體，而本文模擬所用船模不帶附體，這些處理和差異都會增大誤差.綜合考慮這些因素后，取試驗值不確定度UD=20%D.根據文獻[16]所述，因為RFG=2>1，所以無法確定橫向力誤差不確定度.但是其計算結果相對誤差的絕對值在20%附近，屬于工程可接受的誤差范圍，故此處默認橫向力計算結果已完成確認.轉首力矩對比誤差EM為

EM1=DM-SMG1=0.045 9-0.040 0=12.9%D

EM2=DM-SMG2=0.045 9-0.040 1=12.6%D

EM3=DM-SMG3=0.045 9-0.039 9=13.1%D

轉首力矩確認的不確定度UMV為

因為|EM|

4 淺水工況計算結果

4.1 工況描述

計算中，航速V=0.532 m/s，相應的雷諾數Re=2.12×106，弗勞德數Fr=0.084 9；采用上文驗證過的數值方法針對不同水深H(H=1.2，1.5，2.5，3.5，5T，其中T為船舶吃水)下，不同漂角β(β=0°,30°,50°,70°,90°)與較小半徑R(R=1.25L)相組合的回轉運動進行了計算.

4.2 計算結果

4.2.1水深的影響

圖5為不同漂角航態下，船舶所受橫向力隨水深的變化曲線.由圖5可知，無論漂角大小，隨水深的增加，橫向力呈下降趨勢.β=0°時，橫向力明顯小于其他漂角，其值受水深影響較小.β=30°和β=50°時，橫向力相對較大，其值受水深影響較大，變化最為劇烈的水深在1.2～2.5T.

圖5 橫向力隨水深的變化

圖6為不同漂角航態下，船舶所受轉首力矩隨水深的變化曲線.從圖中可以看出，無論漂角大小，轉首力矩在1.2～1.5T變化較為劇烈，且在3.5T之后基本保持不變，也就是說淺水效應逐漸消失.β=0°和β=50°時，轉首力矩隨水深的增加不斷減小；而β=30°時，轉首力矩隨水深的增加總趨勢也在不斷減小，但其減小過程是波動的.

圖6 轉首力矩隨水深的變化

圖7為β=0°和β=50°時，不同水深下船體表面壓力云圖.其中，β=0°為小漂角工況，β=50°為大漂角工況.由圖7b)可知，壓力在首尾處變化梯度較大，正高壓區主要集中在左舷船中處，負高壓區集中在船首和右舷船尾處，這種分布隨水深增加而越趨明顯.與圖7a)相比，圖7b)的壓力云圖則要復雜很多，且其復雜程度隨水深的增加在減小.水深小于2.5T時，船體壓力云圖分布復雜，無明顯規律可循.水深大于2.5T時，壓力云圖分布隨水深增加趨于相同.

圖7 船體表面壓力云圖

4.2.2漂角的影響

圖8為不同水深的回轉工況下，船舶所受橫向力隨漂角的變化曲線.由圖8可知，無論是深水還是淺水，橫向力隨漂角的增大而增大，此外，50°漂角對應的力的值最大，且其值隨水深的增加而減小.

圖8 橫向力隨漂角的變化曲線

從30°漂角之后，數值計算結果與試驗結果誤差在增大，某些漂角的誤差可能已經超出工程可以接受的誤差上限.誤差增大的原因是船體周圍流場隨漂角的增大變得越來越復雜，計算選用的k-ε模型已不能模擬該狀態下的湍流，從而導致計算結果誤差增大.

圖9為不同水深的回轉工況下，船舶所受轉首力矩隨漂角的變化曲線.由圖9可知，當水深大于或等于2.5T時，轉首力矩隨漂角的增大先增大后減小；當水深小于2.5T時，轉首力矩隨漂角的變化也是近似先增大再減小，但同樣也是30°漂角后，其值波動較大，且水越淺波動越明顯.該波動可能是由于越來越明顯的淺水效應導致.

圖9 轉首力矩隨漂角變化的曲線

圖10為H=1.2和5.0T時，不同漂角航態下船體表面壓力云圖.其中，H=1.2T為淺水工況，H=5.0T為深水工況.

圖10 船體表面壓力分布圖

由圖10a)可知，船底壓力隨漂角的增大而增加.0°漂角時，船底還是以較小的壓力為主；30°漂角時，船底處于正壓到負壓過渡的階段.到50°漂角時，船首、尾部出現負高壓，船尾負高壓相對較小.由圖10b)可知，隨漂角的增大，左舷尾部逐漸出現負高壓區，且負壓值呈增大趨勢，整個漂角增大的過程中，船底受力由正壓為主變成了正負壓共存，且正負壓界限分明的分布在首尾處.

淺水中，漂角的增大使得船底壓力由正壓為主變成了負壓為主.該現象可以理解為淺水中漂角的增大引起了船舶的下蹲傾向.深水中，漂角的增大使得船底受力由正壓為主變成了正負壓共存，且正負壓界限分明的分布在首尾處.該現象可以理解為深水中漂角的增大引起了船舶的尾傾.

5 結 論

1) 在30°漂角之后，雖然數值誤差增大，但結果依然可以正確預報船舶所受橫向力和轉首力矩的變化趨勢.可以發現：漂角越大、水越淺，船舶所受橫向力越大;隨漂角增大，船舶所受轉首力矩值波動較大，且水越淺，這種波動變化越明顯.

2) 深水中，漂角越大，數值模擬結果的誤差越大.針對船底受力情況，可以發現：水越淺，漂角越大，船底周圍流場越復雜；淺水中，漂角增大可使船舶發生下蹲現象；深水中，漂角增大可使船舶發生尾傾現象.

需要指出的是，由于缺乏淺水工況試驗數據，本文關于淺水工況所得到的結論只是定性的.今后需要獲取淺水工況下的試驗數據，對本文方法進行進一步驗證，以實現對船舶淺水中低速回轉運動性能的更精確的預報.