小學生計算思維能力調查研究
——以西安市3-5 年級學生為例

王小紅，趙 明

（陜西師范大學 教育學院，陜西 西安 710062）

在當前信息技術快速發展的時代背景下，處理計算機語言成為一種不可避免的技能、一種新的讀寫能力，能讓我們充分有效地參與到信息技術中。因此，當一個人能夠用計算機和其他機器語言讀寫，并能夠用計算機的方式思考時，就被認為是懂代碼的人。計算思維就是指解決問題的認知過程[1]。盡管計算思維可以轉移到不直接涉及編程任務的各種類型的問題上[2]，但計算機編程是使計算思維活躍起來的基礎方法。

隨著信息技術的普及，計算思維越來越被視為創造而不僅僅是消費技術的基本技能[3]，許多國家對引入計算思維的興趣重新點燃。計算思維是新一代學生需要掌握的一套解決問題的技能，長期以來被認為是學生認知發展的重要因素[4]，因此許多國家都將其納入到國家教育課程中。英國等一些歐洲國家從小學開始引入編程教學，并將計算思維納入到課程中。2011 年，美國計算機科學教師協會（CSTA）和計算機協會（ACM），將計算思維納入到小學并且制定了《K-12 計算機科學標準》。2015 年，澳大利將計算思維納入課程目標，上述均反映出各國對計算思維重要性的認識。計算思維已被描述為一項基本的技能，然而業界對其定義以及如何測量和評估尚未達成共識。

國外已有研究證明：在計算思維方面男生和女生存在顯著差異，并且這種現象隨著年級的增加更加突出[5]，那么在我國的基礎教育階段是否存在這種差異現象呢？因此，本文旨在提供一種新的測量計算思維能力的工具，調查在思維初步形成階段的小學生計算思維能力現狀，為后續小學生計算思維能力的培養打好基礎。陳英和與趙笑梅發現：3-5 年級學生在計算機上編寫程序時，已經具備類似問題解決的能力[6]，因此本次研究對象為3-5 年級的小學生。

一、研究綜述

1.計算思維定義

計算思維這一術語包含著概念和思維過程，這些概念和思維過程有助于在不同的領域以一種計算機的方式形成解決方案。2006 年，周以真教授首次提出計算思維并給出正式的定義，認為“計算思維是一種利用計算機科學概念解決問題的方法，不只是計算機科學家應該具有的技能，而是所有人都應具備的技能”[7]。2011 年，其又在此基礎上對計算思維定義進行了修訂，認為“計算思維是一種解決問題的思維過程”[8]。隨著計算思維的不斷深入，學者們紛紛對計算思維進行定義。2011 年，美國國際教育技術協會（ISTE）和計算機科學教師協會（CSTA）聯合認為“計算思維是通過數據收集、數據分析、數據表示、問題分解、抽象、算法和程序、自動化、模擬和并行化等環節進行問題解決的過程。”[9]這也是計算思維最常見的兩種定義，但目前并沒有形成統一。

通過對已有文獻的梳理發現，計算思維定義使用最多的詞匯有：問題解決、抽象、過程、數據、概念、算法、求解、自動化等[10]。并將計算思維歸納為問題解決說、系統說、過程說、活動及方法說、工具說等[11]。

2.計算思維評價

目前關于計算思維的評價并沒有統一的工具，然而驗證過的測量儀器在任何研究領域都是有價值的。近年來，我們發現對中小學的計算思維進行測量和評估的嘗試是值得關注的。

Werner 等人在研究中使用了一個基于Alice 平臺的“仙女評價”系統，試圖調查學生在問題解決過程中對計算思維概念的理解和使用情況[12]。然而，該儀器只針對Alice 編程學習環境，并沒有經過心理測量學驗證。美國克萊姆森大學的研究小組提供了一個互補的觀點。這些學者提出了一個動覺的學習方法（具體學習）來評估五年級和六年級學生的計算思維。為此，他們在Alice 環境中運行序列編程（舞蹈）活動，在物理動覺環境中表示相同的序列。評估工具也結合了這兩種設置，但其心理測量特性尚未報告。

另外，美國科羅拉多大學的小組也提供了一個有趣的研究方向，他們與第一組視頻游戲編程環境中的學生合作，在年輕程序員創建視頻游戲的背景下，設計了計算思維模式圖，用于分析學生編程的游戲，并以圖形化方式與模型相比，每個游戲涉及不同計算思維模式的程度[13]。第二組研究試圖評估學生是否能夠將視頻游戲編程期間獲得的計算思維模式轉移到科學模擬編程的新環境中[14]。針對這一評估，他們開發了計算思維模型的測試工具，其可靠性或有效性尚未報告。

同樣，來自西班牙馬德里大學的學者介紹了一種Dr.Scratch 開源的Web 應用程序，旨在簡單、自動地分析Scratch 編程項目[3]，并提供反饋，可用于提高編程技能和發展學生的計算思維。為了給項目一個整體的計算思維評分，Dr.Scratch 從七個維度推斷程序員的計算思維能力，即問題的抽象、分解、并行、邏輯思維、同步、流程控制、用戶交互和數據表示。其并非嚴格意義上的認知測試，而是Scratch 程序的形成性評價工具。該程序目前正處于驗證過程中。

此外，2003 年在立陶宛誕生了Bebras（國際計算思維挑戰賽），目的是通過計算思維挑戰增強小學生對計算機科學領域的興趣[15]。其每年比賽都會提出一套Bebras 任務，通過計算思維的轉移和投射來解決所面臨的問題，這些問題獨立于任何軟件或硬件，可以提供給任何沒有編程經驗的人。但是目前Bebras 國際比賽只是作為一種推廣計算思維的活動，并不是一個測量工具。

Buffum 等人開發了一套測量5-10 年級學生計算思維發展水平的計算思維能力測試量表，測試總共包括28 項題目，依靠計算概念和使用編程語言的邏輯語法來制定解決問題的能力[16]。目前只有Román-González 等結合標準化心理測試對計算思維能力測試量表進行了驗證，并分析了計算思維能力測試量表的效度[5]。

因此，本次調查將計算思維能力測試量表進行了翻譯，并對小學3-5 年級的學生進行了測試，發現3、4年級的學生是可以完成這份量表的。

3.計算思維性別差異

國外有研究證明學生計算思維能力發展方面存在性別差異。Espino &González 在FLL 機器人競賽調查中發現性別分化明顯，男生的人數多于女生[17]。此結果可能是由于性別的刻板印象而形成的。Román-González等人在西班牙進行計算思維測驗時，發現計算思維在性別方面存在顯著的差異，而且會隨著年級的增長差距越來越大[5]。而Werner 等人在調查學生兩年來計算思維發展與性別的關系時，發現計算思維與性別之間沒有顯著差異[12]，可能是在本次調查中女生僅占36%，男女人數比列差距相對較大的原因。

關于性別差異方面的研究，國外大多數學者認為存在顯著差異，也有一部分人認為沒有差異，但是我國關于這方面的調查相對較少。

二、研究工具

本研究根據Buffum 等人開發的計算思維能力測試（CTT）量表，旨在測量學生的計算思維能力發展水平[16]，包含計算思維的基本概念和使用編程語言的邏輯語法來制定和解決問題的能力。計算思維的基本概念即序列、循環、迭代、條件、函數和變量。這些概念與計算思維三維框架中強調的計算思維概念相一致[18]。計算思維能力測試量表共28 道單選題，每項包括一個或多個計算概念，其中基本序列（4 項）、循環（8 項）、條件（12 項）、函數（4 項）；界面主要以迷宮（23 項）和畫布（5 項）的形式呈現；選項主要以箭頭（20 項）和積木（8 項）呈現問題解決方式（如圖1 所示）。題目中包含計算思維概念和計算思維的實踐，這與計算思維三維框架一致。

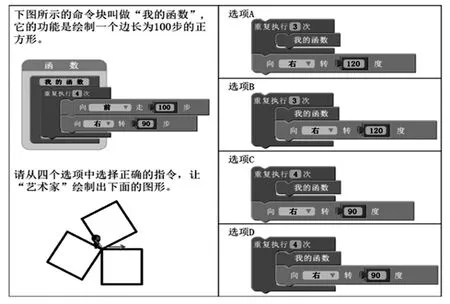
圖1 計算思維能力測試量表題項

三、研究對象與實施

1.研究對象

本研究按照地理位置采用分層多階段整體隨機抽樣方法，把整個西安市13 個區縣劃分為中心城區、郊區和遠郊區三個區域。從每個區域抽取兩個區縣，每個區縣再從小學3-5 年級中隨機抽取一個班級參與測評。

2.問卷的發放與回收

問卷是以問卷星的方式進行發放，通過QQ 群將問卷鏈接轉發給各個區縣的信息技術教師，教師在信息技術課程上督促學生完成或學生在家自主完成問卷，總共回收550 份，其中有效問卷為542 份，有效率達98.5%，不同地區、不同年級的學生樣本如表1 所示。

表1 不同地區、不同年級抽樣學校數和學生數量

四、結果分析與討論

1.描述性統計分析

對所收集到的有效數據整理分析，如表2 所示為整個樣本的計算思維能力測試得分的描述性統計分析，按照28 個題目正確得分之和計算而得（n=542），其中平均分數為13.81，最高分數為27 分，最低分數為4 分。

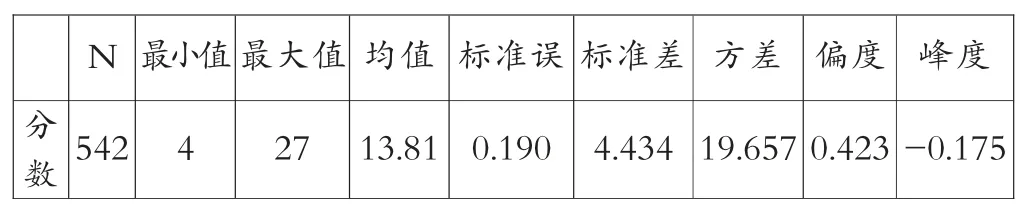
表2 計算思維測試分數描述性統計分析

計算思維能力測試評分的分布直方圖如圖2 所示，評分分布與正態分布曲線吻合。考慮到樣本的容量比較大，分數的雙側顯著性值為sig=0.000，小于0.05，故拒絕了正態性的原假設。

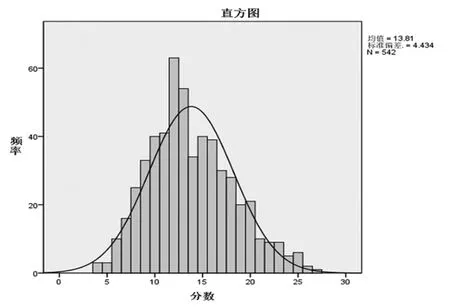
圖2 計算思維測試評分的直方圖

28 項題目的成功率或項目難度指數如圖3 所示，證實了計算思維能力測試量表漸進的難度，在內容方面專家們已經預料到了這點。28 道題目的平均成功率為0.49（中等難度），范圍從0.13（第23 道題具有非常高的難度）到0.95（第1 道題難度非常低）。

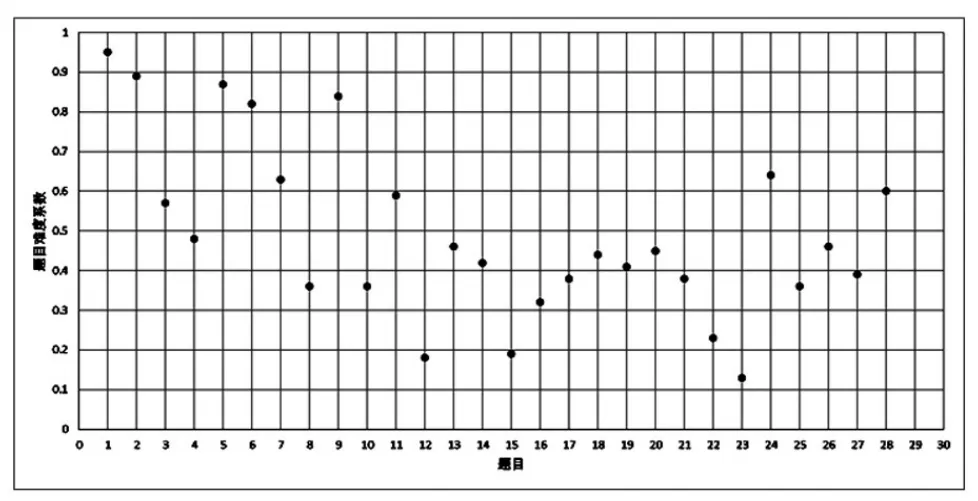
圖3 計算思維測試難度指數

綜上所述可知：計算思維能力測試評分呈正態分布，顯示出適當的變異性，因此可以為目標人群構建適合的尺度；對目標人群而言，計算思維能力測試量表具有適當的難度（中等），而且整個題目的難度越來越大。

2.不同年級分析

按照測試者的不同年級將樣本進行分割，得到表3所示的描述性統計分析。由于六年級學生面臨升學壓力，本次測試的調查對象為小學高年級中的3-5 年級。

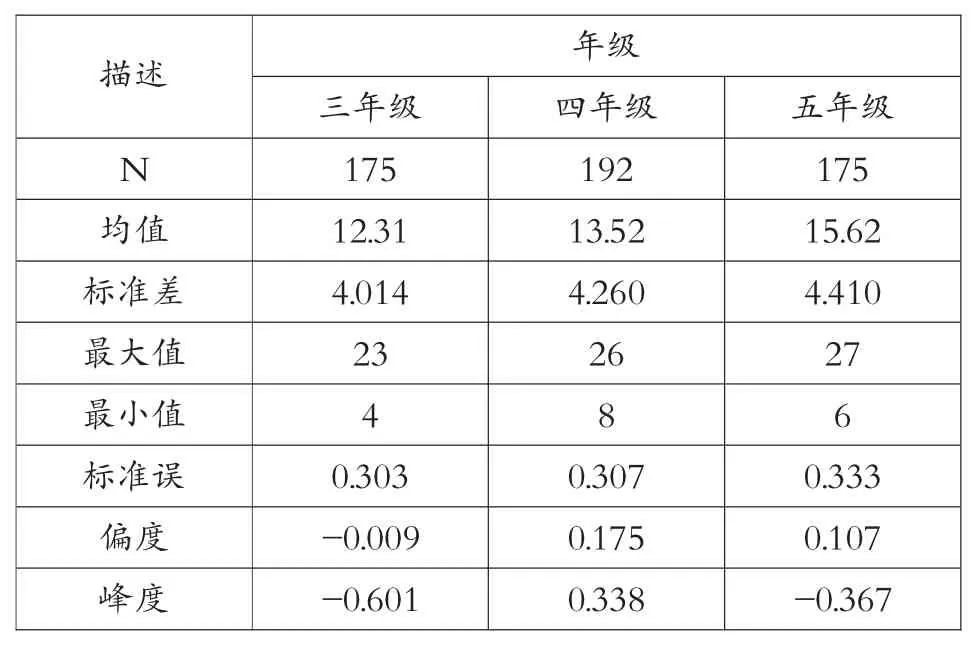
表3 不同年級計算思維測試評分描述統計分析

圖4 計算思維測試難度指數

不同年級學生計算思維能力測試得分如圖4 所示，四年級出現了離散值情況，在計算思維能力測試中獲得了26 分的評分。單因素方差分析顯示計算思維能力測試得分與年級在統計學上有顯著差異（F=27.419，p＜0.01），說明計算思維能力測試得分隨著年級的增加而增加，這個結果與我們的假設一致，即計算思維是一種解決問題的能力，與受試者的認知發展聯系起來[19]。

3.不同性別分析

如表4 所示，在計算思維能力測試評分中男女生的得分在統計學上有極其顯著的差異（P=0.000,p＜0.01）。效應量測量Cohen's d 為0.51，被認為是一種中度效應。按照年級來分析性別差異，計算思維能力測試評分中男生的均值始終高于女生，性別差異在四年級（t=2.507，p＜0.05）和五年級（t=4.452，p＜0.01）有統計學意義。

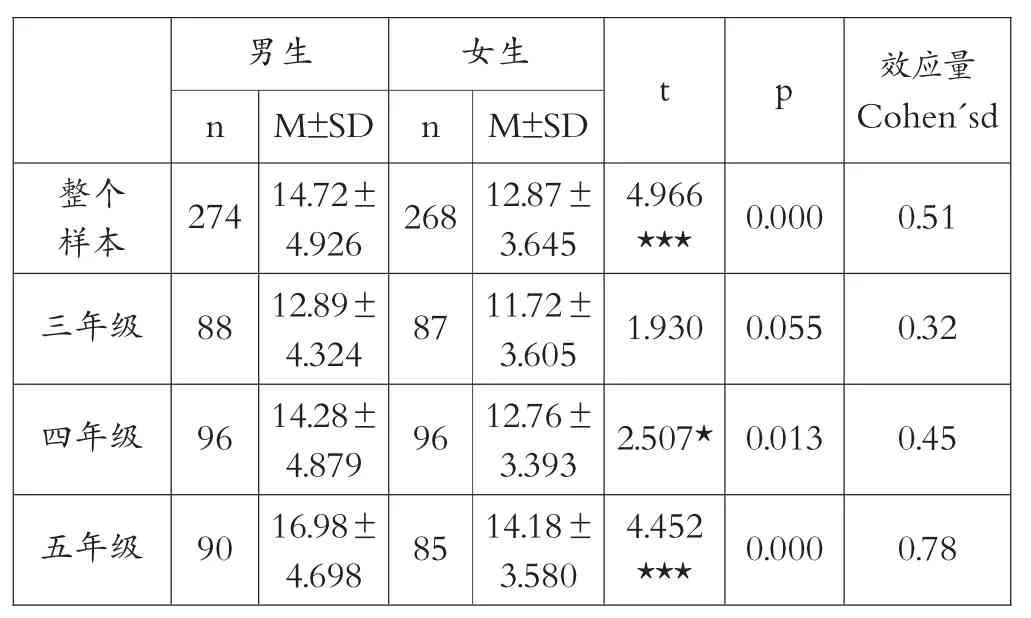
表4 計算思維能力測試對立樣本T 檢驗

可見計算思維能力的性別差異是一個漸進的差異，隨著年級的升高而增加(如圖5 所示)。這與之前Bebras 的調查研究中的性別差異結果一致[20]。

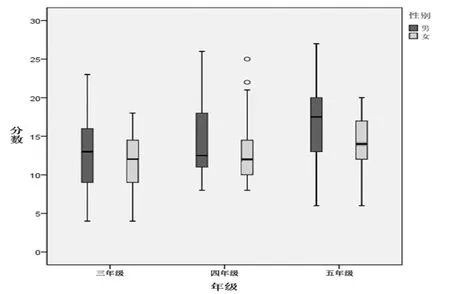
圖5 計算思維測試性別差異

4.信效度檢驗

計算思維能力測試量表的內部一致性信度Alpha的值為0.737（見表5），表明信度良好。對不同年級學生評分的可靠性進行研究時，發現四年級學生的回答準確性更低，三年級的準確性是最高的，這與年級越高準確性越高的結果呈相反趨勢。

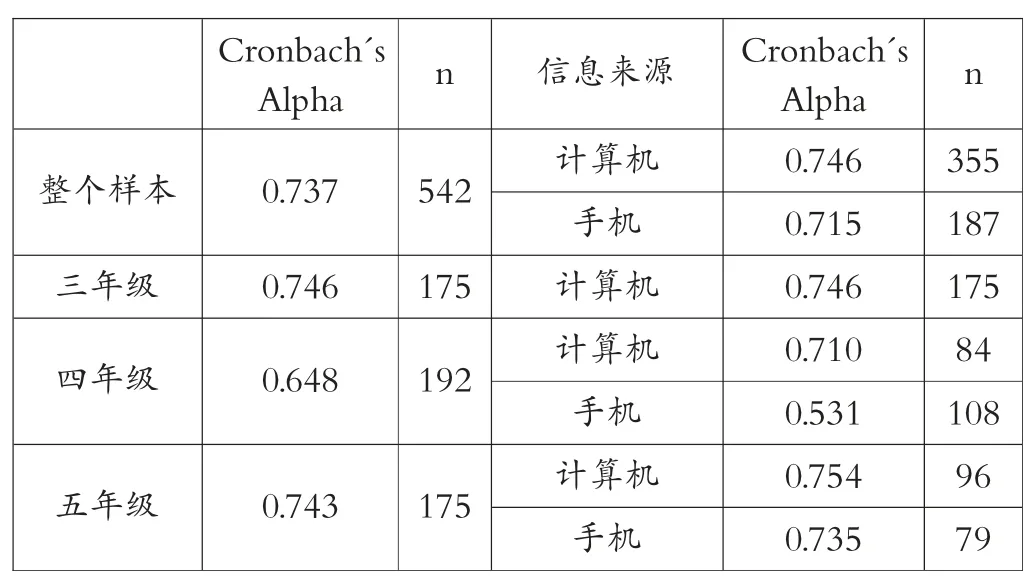
表5 計算思維能力測試內部一致性

但是對計算思維能力測試數據來源進行分析發現，來源于計算機的數據正確性更高，這可能與在教師的監督下學生更認真、更集中精力完成測試有關，避免了學生隨意填寫的可能性。這一解釋得到了在計算機上進行計算思維能力測試和在手機上進行計算思維能力測試得分結果的支持，使用計算機的平均得分為13.90，使用手機的平均得分為13.63。

5.計算思維概念維度分析

計算思維能力測試量表中計算思維概念包括五個維度，即順序、循環、條件、并行和函數，數據分析如表6所示，從中可以看出學生在計算思維概念方面，順序概念是相對較好掌握的，而并行和條件是相對較難掌握的。而且隨著年級的增高，所有計算思維概念的維度都會有所提升。所有的計算思維概念維度中都是男生平均得分高于女生平均得分，但是性別差異僅在三年級函數概念方面存在顯著差異，男生分數明顯高于女生分數（p=0.014＜0.05）,五年級學生在并行概念方面存在顯著的性別差異，男生分數明顯高于女生分數（p=0.012＜0.05）。

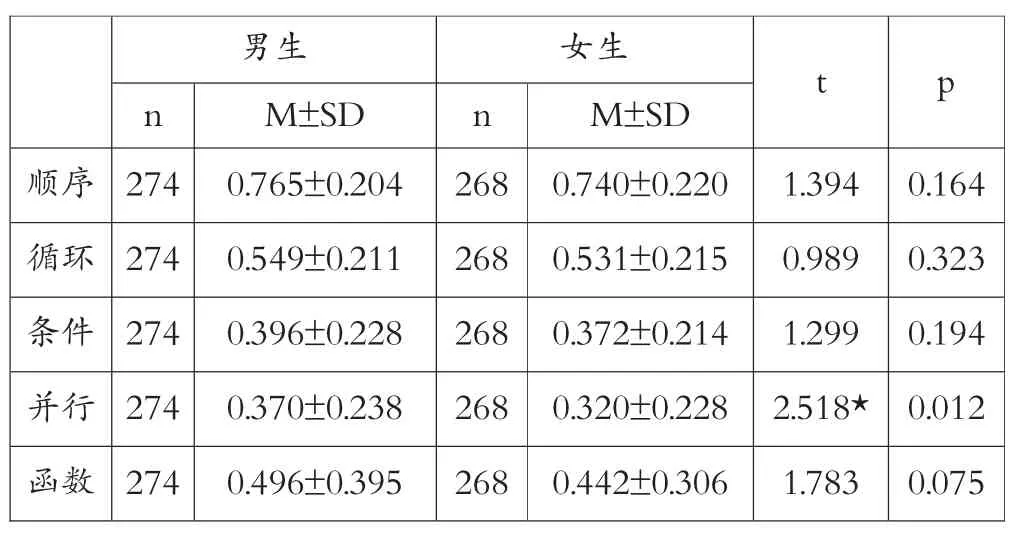
表6 計算概念各維度對立樣本T 檢驗

6.影響和限制

計算思維能力測試量表有一些優勢，開發者預定的測驗對象為5-10 年級，但在試測中發現可以應用于3、4 年級的學生，這個階段的學生思維能力已經形成，因此可以衡量沒有編程經驗的3-10 年級學生的計算思維水平。計算思維能力測試可以用來收集量化數據，也可以用于篩選和早期發現對編程任務解決能力較高的學生，并可以在培養學生計算思維的課程和項目前后進行評估，而在已有的文獻中將其應用于收集定性數據。

然而計算思維能力測試量表也有它的局限性，主要表現為以下幾個方面：①計算思維能力測試量表提供靜態和非文本化的總結性評估。因此需要與其他形成性迭代測評工具結合使用，如針對不同編程環境的評價標準，支持Scratch 編程環境的Dr.Scratch 的評估、Ninja Code Village 和Grover 等人開發的針對Blockly 的工具[21],以及適用于Agent Sheets 的計算思維模式CTP 圖形[13]。②計算思維能力測試量表過于關注計算思維框架中的計算概念，僅有一部分涵蓋計算實踐，而忽略了計算觀念維度，因此應該與建立調查學生計算思維能力（CTS）態度的量表[22]相結合。③由于計算思維能力測試量表的設計是選擇題，因此可以在較低的認知復雜程度下測量計算思維。采用多種手段并用的方法，結合CTT、Bebras 和Dr.Scratch 以及訪談等測評工具，用開放的復雜問題喚起項目的正確算法，以及在解決方案中讓學生將計算思維轉移到不同的領域，測量更高復雜程度的計算思維。

五、結論

本文提供了一種新的計算思維評估工具，通過計算思維能力測試量表對西安市小學3-5 年級542 名學生的計算思維能力發展情況進行了調查，并分析了小學階段學生計算思維能力的性別差異。研究結果顯示，3 年級的學生已經具備基本的計算思維能力，并且隨著年級的增長計算思維能力有所提升，同時男女之間計算思維能力的差異越來越顯著，整體上男生的計算思維能力要高于女生。因此，筆者建議要在這種現象形成初期，對學生進行干預以避免該現象的持續加深，并在教學干預中應該注重相關知識的傳授。