基于改進支持向量回歸的港機剩余使用壽命預測

吳沛冬　萇道方　陸后軍　高銀萍

摘要：

為解決標準支持向量回歸（support?vector?regression，?SVR）在預測港機剩余使用壽命時，誤差程度不同的數據會被施以相同程度的懲罰，從而導致預測精度不足的問題，通過對每個數據的懲罰系數添加各自的誤差比例，使每個數據的懲罰系數與各自的誤差程度成比例，降低誤差數據對整體預測精度的影響。實驗表明，這種改進SVR相對于標準SVR在不降低計算效率的前提下能有效提高預測精度，并擁有良好的泛化能力。

關鍵詞：

支持向量回歸（SVR）;?剩余使用壽命;?懲罰系數;?預測精度

中圖分類號：U691.5

文獻標志碼：A

Prediction?of?remaining?useful?life?of?port?machine?based?on

improved?support?vector?regression

WU?Peidonga，?CHANG?Daofanga，?LU?Houjunb，?GAO?Yinpinga

（a.Institute?of?Logistics?Science?&?Engineering;?b.Logistics?Engineering?College，

Shanghai?Maritime?University，?Shanghai?201306，?China）

Abstract：

When?the?standard?support?vector?regression?（SVR）?is?adopted?to?protect?the?remaining?useful?life?of?port?machine，?the?data?with?different?degrees?of?error?are?given?the?same?degree?of?punishment，?which?leads?to?insufficient?prediction?accuracy.?In?order?to?solve?the?problem，?the?respective?error?ratio?is?added?to?the?penalty?coefficient?of?each?data，?so?that?the?penalty?coefficient?of?each?data?is?proportional?to?the?respective?error?degree，?and?the?influence?of?the?error?data?on?the?overall?prediction?accuracy?is?reduced.?Experiments?show?that，?this?improved?SVR?can?effectively?improve?the?prediction?accuracy?and?have?good?generalization?ability?compared?with?the?standard?SVR?without?reducing?the?computational?efficiency.

Key?words：

support?vector?regression?（SVR）;?remaining?useful?life;?penalty?coefficient;?prediction?accuracy

收稿日期：?2018-12-17

修回日期：?2019-03-25

基金項目：?上海臨港地區智能制造產業專項（ZN2018010105）

作者簡介：

吳沛冬（1995—），男，江蘇南通人，碩士研究生，研究方向為機器學習，（E-mail）419224205@qq.com;

萇道方（1978—），男，河南封丘人，教授，博導，博士，研究方向為供應鏈設計與運營、物流系統運作與優化，

（E-mail）changdaofang@126.com

0?引?言

隨著港機設備不斷地更新換代，它們的使用和維護成本也在不斷增加，這導致大部分港機制造企業開始由即時維護策略向預測性維護策略進行轉變，以此來降低維護成本[1]。預測性維護能夠根據設備的相關現場數據，通過回歸預測模型預測出設備的剩余使用壽命（remaining?useful?life，?RUL）[2]。在對港機的現場預測中，采集到的現場數據往往特征復雜、數量龐大且包含誤差，這將導致那些處理線性問題能力強但處理非線性問題能力一般的方法的預測精度難以保證。

以往對港機維護的研究大多是對港機進行即時狀態監測、維修保養，如：安志家等[3]根據天津港港機工作特點，僅將設備狀態監測工作與設備日常點檢、維修保養及設備故障診斷結合;商偉軍[4]使用港機金屬結構失效診斷和控制維修技術，對港機運行狀態進行預測。在以上的研究中，學者們雖然提出了很好的港機維護方法，但對預測性維護的應用依然較少。本文針對港機在現實維護中會遇到的不確定性和隨機性因素，使用預測性維護設計預測港機RUL。

VAPNIK[5]在1995年提出了支持向量回歸（support?vector?regression，?SVR），基于VC（Vapnik-Chervonenkis）維理論和結構風險最小原理的SVR擁有更高的泛化能力。SVR基于結構風險最小原理，將置信范圍值最小作為優化目標，將訓練誤差構造為約束條件，以此來提高泛化能力;在求解時，結構風險最小原理使SVR轉化為一個二次規劃問題進行求解，以此來保證解的全局最優性;決策函數只由少數支持向量決定，因此SVR在處理高維度的樣本時計算復雜度不受樣本維度的影響。

在過去的研究中，學者們不斷對SVR的應用進行優化。YE等[6]基于小波和SVR構建了一種徑向分布系統中的故障定位方法。

NIETO等[7]采用粒子群優化技術并與支持向量機結合對引擎的RUL進行了預測。SU等[8]運用自回歸滑動平均模型與在線最小二乘SVR相結合的方法對引擎故障進行了在線預測。CHEN[9]通過遺傳算法搜索SVR的最優參數，構建了基于遺傳算法的SVR模型，并驗證了SVR在回歸上的優越性。在這些研究中，學者們雖然對SVR進行了改進，但大多是通過一些智能算法對SVR進行優化的，而本質上SVR的性能并沒有發生改變。QUAN等[10]運用連續過松弛的方法對SVR進行了改進，提高了SVR的運算效率。陳懿冰等[11]通過動態加權函數使SVR在時序金融預測中效果更好。QUAN等[12]通過對SVR的目標函數進行優化，加快了計算效率。盡管在上述研究中SVR良好的回歸能力已經被廣泛應用，但其對預測準確性的提升有待研究。

本文使用SVR對港機的RUL進行訓練和預測，用來預測的數據會因港機運轉現場的各種環境因素影響出現不同程度的隨機誤差，而標準SVR會對這些包含不同程度誤差的數據賦予相同的懲罰系數，在不將懲罰系數設置過大造成訓練欠擬合的情況下，包含更大誤差的數據會更嚴重地降低整體的預測精度。針對這個問題，本文通過對包含不同程度誤差的數據賦予對應誤差比例的懲罰系數，減小誤差較大的數據對預測精度的影響。

本文使用故障數據集中較為權威的Turbofan數據集來驗證改進SVR的預測效果[13]，選取均方根誤差[14]作為評價指標，驗證預測精度，這是考慮到它能在同一數量級下最大程度體現預測誤差。

1?算法分析

1.1?標準SVR

SVR首先要將輸入的非線性數據映射到高維空間進行線性的回歸估計，這種變換是通過核函數

K（xi，xj）=Φ

（xi）·Φ（xj）實現的，

Φ表示將輸入樣本映射到高維特征空間的映射函數。

給定訓練集

{（xi，y），?i=1，2，…，n}，其中

xi∈Rk是第i個訓練樣本的輸入，是一個k維列向量

xi=（xi1，xi2，…，xik）T，

y是這個訓練樣本對應的標簽，

y=（y1，y2，…，yn）T。由此可以構造回歸函數：

式中，φ（x）為非線性映射核函數，ω和b

分別為相應的系數矩陣和偏移常量，

b=（b1，b2，…，bn）T。

在此回歸函數的基礎上，通過添加表示誤差容忍度的不靈敏損失參數ε，定義線性不敏感損失函數：

即當y與經過訓練得到的估計值f（x）之間的距離大于ε時才會計算誤差，否則記誤差為0。

以式（2）為固定條件使置信范圍最小化，如圖1所示，加入表示超出允許誤差程度的松弛變量ξ和

式（3）中C是懲罰因子，表示允許犯錯誤的程度，這里設置為常數，表示每個點的懲罰因子都是相同的。

為降低求解復雜度，引入拉格朗日乘子αi和α*i，將問題轉化成對偶形式并求解得到部分不為0的參數

（α*i-αi），這些參數就是問題中的支持向量，由它們得到訓練過后的決策回歸函數：

以上即為標準SVR的原理，下面對提高其預測精度的能力進行改進。

1.2?改進SVR

在標準的SVR中，懲罰因子C對每個點的懲罰作用是相同的，在實際對設備RUL的預測中，采集到的數據往往存在隨機誤差，對這些包含隨機誤差的數據賦予相同的懲罰因子，會導致包含不同程度誤差的數據訓練擬合度相同，這就會使訓練中誤差較大的項出現過擬合，從而出現整體預測結果偏差較大的現象。為解決這個問題，本文通過對包含不同程度誤差的數據賦予對應誤差比例的懲罰系數，來減小誤差較大的數據對預測精度的影響，

具體執行方式是為原本固定的懲罰系數C添加一個誤差比例pi。pi的表達形式如下：

2?算例分析

Turbofan數據集包括訓練集和測試集，其中：訓練集提供了100個引擎從正常運行到性能衰退的完整的循環過程;測試集提供了每個引擎的一組工作時間序列，但這些序列的終止狀態未必是該引擎最終的性能衰退狀態。數據集中的每個引擎都有24個監控參數，其中3個參數用來設定引擎的初始狀態，另外21個參數見表1。

根據NIETO等[7]的研究，能夠參與引擎RUL預測的參數包括T24、T30、T50、P30、Nf、Nc、Ps30、phi、NRf、NRc、BPR、htBleed、W31、W32這14個傳感器所測量的參數[7]。

本文通過均方根誤差

來評價SVR的預測準確度，ERMS越小說明預測效果越好。分別通過100個引擎的預測精度來評價SVR的泛化能力。為能夠從整體預測效果上看出改進SVR的改進效果，計算各種算法在整體訓練集下的期望損失并進行對比，即計算并對比標準SVR、改進SVR、線性回歸和隨機決策森林對100個引擎預測結果ERMS的期望值;分別通過100個引擎的訓練時間來評價SVR的計算效率，訓練時間越短說明計算效率越高。式（13）中的n為每個引擎時間序列數量之和。

本文方法均通過Python?3.5來編寫實現，核函數使用泛化能力較好且在各領域表現出色的如式（14）所示的徑向基核函數，

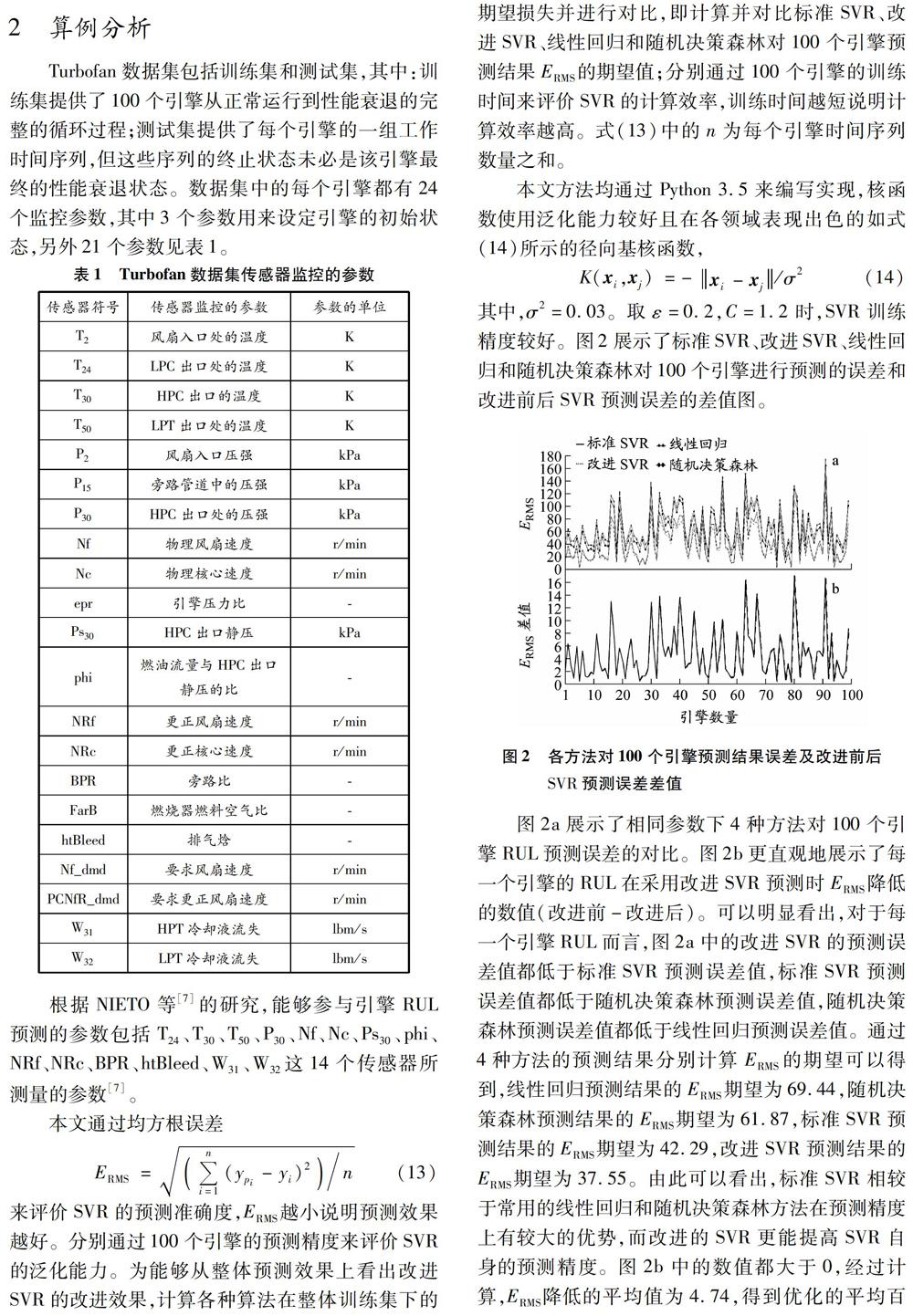
圖2a展示了相同參數下4種方法對100個引擎RUL預測誤差的對比。圖2b更直觀地展示了每一個引擎的RUL在采用改進SVR預測時ERMS降低的數值（改進前-改進后）。可以明顯看出，對于每一個引擎RUL而言，圖2a中的改進SVR的預測誤差值都低于標準SVR預測誤差值，標準SVR預測誤差值都低于隨機決策森林預測誤差值，隨機決策森林預測誤差值都低于線性回歸預測誤差值。通過4種方法的預測結果分別計算ERMS的期望可以得到，線性回歸預測結果的ERMS期望為69.44，隨機決策森林預測結果的ERMS期望為61.87，標準SVR預測結果的ERMS期望為42.29，改進SVR預測結果的ERMS期望為37.55。由此可以看出，標準SVR相較于常用的線性回歸和隨機決策森林方法在預測精度上

有較大的優勢，而改進的SVR更能提高SVR自身的預測精度。圖2b中的數值都大于0，經過計算，ERMS降低的平均值為4.74，得到優化的平均百分比為10.89%。這代表對每個引擎而言，根據預測結果計算所得的ERMS都更小，預測精度都更高，且100個引擎全部得到優化的結果可以證明，改進SVR具有良好的泛化能力。

為證明針對標準SVR的改進沒有提高算法復雜度從而提高算法的計算時間，圖3展示了標準SVR、改進SVR、線性回歸和隨機決策森林方法預測各引擎RUL花費的時間對比。

圖3a展示了相同參數下，改進前后的SVR對100個引擎RUL預測花費時間的對比。圖3b更直觀地展示了每個引擎的RUL采用改進前后SVR預測所花費的時間差（改進前-改進后）。由于每個引擎RUL的預測時間較短，從圖3a難以看出改進前后的SVR預測每個引擎RUL花費的時間差，但總體可以觀察到4種方法的預測曲線基本重合。從圖3b可以明顯看出，對于每一個引擎而言，改進前后SVR預測其RUL花費的時間之差都在0上下波動。經過計算可知，改進前后的SVR預測各個引擎RUL花費時間的平均差值為9×10-5，考慮到每次計算時計算機狀態的不確定，該差值可以忽略，說明該改進方法并未降低SVR的計算效率。

3?結?論

針對標準SVR在對港機剩余使用壽命（RUL）的預測中，對誤差程度不同的數據采取相同的誤差懲罰，導致預測精度不足的現象，本文對標準SVR進行改進，對懲罰系數添加一個比例系數，調節不同誤差數據的懲罰力度，加大對誤差較大數據的懲罰，降低大誤差數據對整體預測的影響，并將其應用Turbofan數據集進行驗證。結果表明，該改進方法的預測效果受異常數據干擾較小，且能夠在不降低標準SVR計算效率的前提下，使回歸線能夠向更準確的方向偏移，提高預測精度，并具有良好的泛化能力。在已經對港機RUL預測精度作出改進的前提下，將進一步研究如何提高港機維護的預測效率。

參考文獻：

[1]BAPTISTA?M，?SANKARARAMAN?S，?MEDEIROS?I?P?D，?et?al.?Forecasting?fault?events?for?predictive?maintenance?using?data-driven?techniques?and?ARMA?modeling[J].?Computers?&?Industrial?Engineering，?2018，?115：?41-53.?DOI：?10.1016/j.cie.2017.10.033.

[2]ZIO?E，?MAIO?F?D.?Fatigue?crack?growth?estimation?by?relevance?vector?machine[J].?Expert?Systems?with?Applications，?2012，?39（12）：?10681-10692.?DOI：?10.1016/j.eswa.2012.02.199.

[3]安志家，?鄭奕龍，?王鑫偉.?狀態監測在港機設備維護中的應用[J].?設備管理與維修，?2016（8）：?86-89.?DOI：?10.16621/j.cnki.issn1001-0599.2016.08.42.

[4]商偉軍.?港機結構失效診斷、控制和維修方法研究及應用[D].?上海：?同濟大學，?2003.

[5]VAPNIK?V.?The?nature?of?statistical?learning?theory[M].?Springer，?1999：?267-287.?DOI：?10.1007/978-1-4757-2440-0.

[6]YE?Lei，?YOU?Dahai，?YIN?Xianggen，?et?al.?An?improved?fault-location?method?for?distribution?system?using?wavelets?and?support?vector?regression[J].?International?Journal?of?Electrical?Power?&?Energy?Systems，?2014，?55（2）：?467-472.?DOI：?10.1016/j.ijepes.2013.09.027.

[7]NIETO?P?J?G，?GARCA-GONZALO?E，?LASHERAS?F?S，?et?al.?Hybrid?PSO-SVM-based?method?for?forecasting?of?the?remaining?useful?life?for?aircraft?engines?and?evaluation?of?its?reliability[J].?Reliability?Engineering?&?System?Safety，?2015，?138：?219-231.?DOI：?10.1016/j.ress.2015.02.001.

[8]SU?Shengchao，?ZHANG?Wei，?ZHAO?Shuguang.?Online?fault?prediction?for?nonlinear?system?based?on?sliding?ARMA?combined?with?online?LS-SVR[C]//Proceedings?of?the?33rd?Chinese?Control?Conference.?IEEE，?2014：?3287-3291.?DOI：?10.1109/ChiCC.2014.6895482.

[9]CHEN?Kuan-Yu.?Forecasting?systems?reliability?based?on?support?vector?regression?with?genetic?algorithms[J].?Reliability?Engineering?&?System?Safety，?2007，?92（4）：?423-432.?DOI：?10.1016/j.ress.2005.12.014.

[10]QUAN?Yong，?YANG?Jie，?YE?Chenzhou.?Successive?overrelaxation?for?support?vector?regression[J].?Journal?of?Software，?200：?648-651.?DOI：?10.1007/3-540-39205-X_109.

[11]陳懿冰，?張玲玲，?聶廣禮，?等.?基于改進的支持向量回歸機的金融時序預測[J].?數學的實踐與認識，?2012，?42（4）：?38-44.?DOI：?10.3969/j.issn.1000-0984.2012.04.006.

[12]QUAN?Yong，?YANG?Jie，?YAO?Lixiu，?et?al.?An?improved?way?to?make?large-scale?SVR?learning?practical[J].?EURASIP?Journal?on?Advances?in?Signal?Processing，?2004（8）：?1135-1141.?DOI：?10.1155/S1110865704312096.

[13]YANG?Zhe，?BARALDI?P，?ZIO?E.?A?comparison?between?extreme?learning?machine?and?artificial?neural?network?for?remaining?useful?life?prediction[C]//2016?Prognostics?and?System?Health?Management?Conference.?IEEE，?2017：?1-7.?DOI：?10.1109/PHM.2016.7819794.

[14]CHAI?T，?DRAXLER?R?R.?Root?mean?square?error?（RMSE）?or?mean?absolute?error?（MAE）？—Arguments?against?avoiding?RMSE?in?the?literature[J].?Geoscientific?Model?Development，?2014，?7（3）：?1247-1250.?DOI：?10.5194/gmd-7-1247-2014.

（編輯?賈裙平）