結構與空氣噪聲輻射的等效面聲源預測

莊 超,劉漢光,蘇俊收,劉 杰

(1.徐工集團 江蘇徐工工程機械研究院有限公司,江蘇 徐州 221004; 2.徐工集團 高端工程機械智能制造國家重點實驗室,江蘇 徐州 221004)

傳統結構噪聲輻射預測的一般過程是通過試驗或仿真獲取結構表面的振動加速度、位移等,以此為邊界條件，應用聲學有限元或邊界元的方法計算輻射聲場[1].然而,對于一些復雜結構或者工況,試驗測試工作量繁重,仿真所需的激勵獲取困難,仿真結果準確度難以保證.于是,等效聲源方法應運而生.作為一種復雜聲源聲場的預測技術,等效聲源方法采用了簡單離散聲源替代復雜聲源作為邊界條件用于輻射聲場預測.Chen等[2]提出在聲輻射結構表面布置等效聲源,并通過匹配結構邊界速度預測輻射聲場.李加慶等[3]基于等效聲源法應用波疊加法實現聲場重構.魏應三等[4]采用等效源方法建立了輻射體表面法向振速到場點聲壓的傳遞函數,實現了輻射聲場的數值預測,同時證明了存在最優等效聲源位置以滿足輻射體表面法向振速的最佳匹配.王斌等[5]提出基于單元輻射疊加的表面振速預測輻射聲場,利用剛性障板上單位速度振動活塞面的輻射聲壓，直接建立表面振速與輻射聲壓之間的傳遞關系,以此表面振速進行加權、求和便得到總的輻射聲壓.但是,上述方法需要已知結構表面振速.

點聲源替代[6-7]也是一種應用較為普遍的等效聲源預測方法,假設大尺寸聲源表面可以由一系列小尺寸的聲源面替代,其中,每一個小尺寸聲源面包含一定數量的具有特定體積速度和隨機相位的點聲源.點聲源替代技術分為兩種實現方法——直接計算方法和基于互易性數值計算方法,兩者均基于Verheij等[8]提出的等效聲功率體積速度方法.直接計算方法[6,9]可通過聲強測試計算出等效小尺寸聲源面的體積速度作為輻射聲場計算的邊界條件,該方法忽略了相位信息,然而準確的聲場數值計算須同時提供聲源的幅值和相位信息.為了解決該矛盾,可以分別計算每個替代聲源面的貢獻量后求和,但對于實際大尺寸的復雜聲源輻射聲場計算將耗費大量的計算時間.同時,雖可通過提供隨機相位信息[10-11]進行計算,對于實際復雜聲源的聲場預測結果并不盡如人意.于是,Augusztinovicz等[12]提出基于互易性數值計算方法,首先計算替代聲源的強度大小,然后基于互異性原則計算每個替代聲源到測點的傳遞函數,最后在綜合計算等效聲源的輻射聲場,可以取得較好的預測精度.然而,應用基于互易性的復雜聲源聲場預測方法,在模擬中大尺寸聲源的輻射聲場時,如果需要獲得的精確度越高,就需要越多的聲源替代面,相應地須分別計算相當大規模和數量的傳遞函數.

本文受點聲源替代技術的啟發,考慮聲學邊界元的Dirichlet邊界條件,將復雜聲源的表面近場復聲壓信息作為邊界條件,提出了結構與空氣噪聲輻射的等效面聲源預測方法.首先,將復雜聲源作為一個整體,建立虛擬包絡面并劃分若干子區域;然后,通過噪聲測試獲取每一個子區域中心的測點聲壓信息,包括頻段范圍內的幅值與相位等;最后,將聲壓賦予虛擬包絡面網格作為聲學邊界條件，結合聲學邊界元法預測其輻射聲場分布和聲功率.相比于點聲源替代技術,該方法用面聲源做等效,可以克服點聲源所固有的理想化屬性,更能貼近實際復雜聲源.本文將該方法應用于矩形箱振動與氣動發聲系統的等效聲源替代,對比了其輻射聲功率、輻射聲場任一點聲壓的實驗值和預測值,證明了預測方法的有效性,同時研究了等效面區域數量對預測結果的影響.

1 近場聲壓等效聲源模型

以振動發聲系統為例說明近場聲壓等效聲源模型建立過程.圖1為一個結構輻射聲場的包絡體,通過實驗或者仿真,可以獲取包絡體各面內任意一點位置的復聲壓信息.將上述包絡體各面劃分為規則的區域,如圖2所示.

圖1 結構輻射聲場包絡體Fig.1 Envelop of structural radiation sound field

圖2 聲源等效模型Fig.2 Equivalent acoustical model

每個區域賦以其中心點的聲壓信息,包括聲壓實部和虛部,這樣就形成了結構噪聲近場聲壓等效聲源,以此作為聲學邊界條件，建立相應聲學數值模型并求解.這樣不需要獲取結構表面的真實振動響應,即可計算輻射聲場,避開獲取實際振動激勵的工作和可能的困難.

2 數值計算的理論基礎

Chen[2]首次將邊界積分方程應用于聲輻射問題,聲學問題控制方程Helmholtz微分方程為

(1)

式中:p為聲壓;k為波數,k=ω/c，ω為頻率，c為聲速.控制方程包含Dirichlet,Neumann以及Robin等3類邊界條件.對于穩態聲場外問題,還需要滿足遠場Sommerfeld輻射邊界條件，即

(2)

式中：n為邊界的法線方向；r為源點到場點的距離.

借助Helmholtz方程的基本解u*與格林公式,則

(3)

式中：Q為場點.

(4)

式中：Ω為求解域；Γ為求解域的邊界.

將式(1)和式(3)代入(4)可得到如下積分方程:

(5)

將式(5)中的源點P移到求解域的邊界,獲得邊界上的聲壓及其外法向質點振速之間的邊界積分方程

(6)

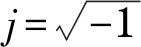
(7)

為了數值求解邊界積分方程,需要將聲學域的邊界劃分成有限個單元,這里用二維三角形面單元.將邊界離散成Ne個單元,則邊界積分式(6)變為

(8)

式中:Γe為單元e的邊界.

對于邊界上所有N個節點,可以得到N個方程,用矩陣的形式表示為

(9)

式中:H,G為系數矩陣;P,V為邊界節點上的聲壓及其外法向質點振速組成的列向量.

將式(9)進行變換,使未知量移到左邊,已知量移到右邊,形成線性方程組

(10)

式中：A為系數矩陣；X為未知向量；b為已知向量.

求解上述方程組,就可以得到所有邊界節點上的p和vn值.

在求得所有邊界節點上的p和vn值后,區域內任一點的聲壓可由式(5)的離散化形式來計算,vn可由式(5)的導數得到,即

(11)

本文通過實驗方法,獲取邊界上復聲壓,作為Dirichlet邊界條件,即式(6)中的p,以實現聲學邊界積分方程的計算,根據式(5)得到輻射聲場域內任一點的聲壓.

3 應用算例

在如圖3所示的半消聲室內進行測試,矩形鐵質箱體尺寸為1 000 mm×80 mm×600 mm,在其上表面和右側面設置有400 mm×200 mm的長方形開口,箱體由橡皮繩吊起,其底部中心為激振器的激勵點,測試時對激振器輸入0～2 048 Hz的隨機猝發信號,激振力在-39～39 N范圍內波動,在激振器的作用下,矩形箱體產生結構振動噪聲.在矩形箱表面布置近場傳聲器組,獲取等效聲壓源面的聲壓信息,同時在輻射聲功率級的相應測點位置,布置6個遠場傳聲器,以測試該發聲系統的輻射聲功率級,為等效面聲源仿真提供精確的對比數據.

3.1 振動發聲系統16個等效面聲源預測

經實驗測試獲取矩形箱振動時近場表面區域的聲壓信息之后,建立了如圖4的含16個等效面聲源的仿真模型,每一個等效面賦以相應位置測點的聲壓數據作為邊界條件,共同組成了矩形箱振動發聲系統的等效聲源模型.數值計算時,在同樣的坐標位置設置測試輻射聲功率的6個場點,以計算等效聲源系統的輻射聲功率級.

圖3 矩形箱結構噪聲近場與遠場測試Fig.3 Near-field and far-field measurement of rectangular box structural noise

圖5給出了實驗測試的矩形箱振動發聲系統輻射聲功率級與16個等效面聲源數值計算獲取的輻射聲功率級頻譜曲線,預測值基本圍繞實驗值上下波動,最大偏差10 dB(A)左右.

圖5 16個等效面聲源仿真結果Fig.5 Simulation results of equivalent sound mode with sixteen regions

3.2 振動發聲系統70個等效面聲源預測

嘗試增加更多的近場表面測點,將矩形箱表面劃分更多的區域,即用更多的等效面聲源來模擬矩形箱的振動發聲系統.建立了如圖6所示的70個等效面聲源計算模型,與實驗測試的矩形箱表面區域劃分一致,各等效聲源面賦以相應的測點聲壓信息,包含幅值和相位.

圖6 70個等效面聲源仿真模型Fig.6 Equivalent sound modes with seventy regions

圖7給出了實驗測試與等效聲源面數值計算獲取的矩形箱振動發聲系統的輻射聲功率級頻譜圖,預測值圍繞實驗值做小范圍波動,貼合度較高,最大偏差5 dB(A)左右.

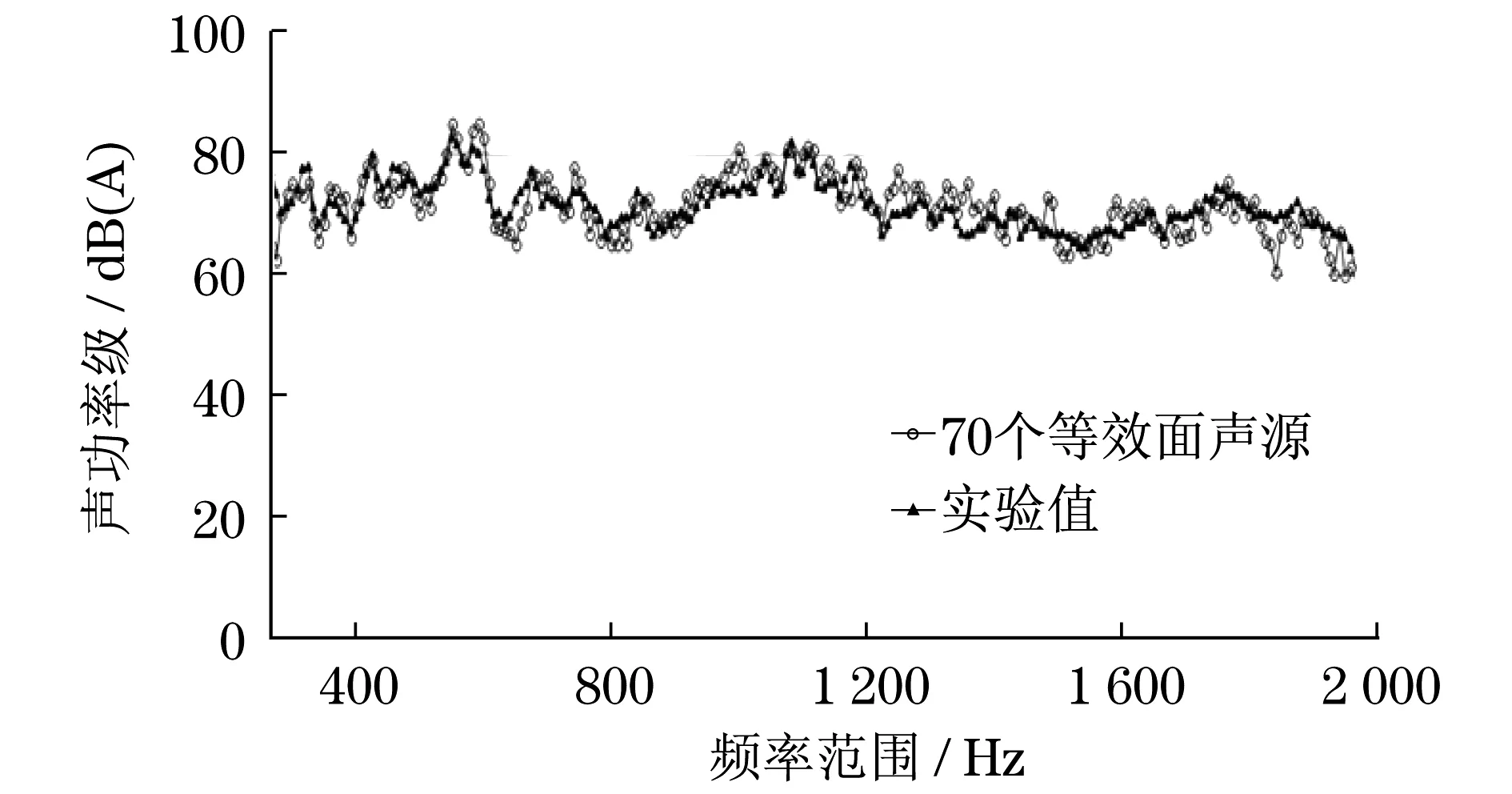
圖7 70個等效面聲源仿真結果Fig.7 Simulation results of equivalent sound model with seventy regions

此外,本文將實驗測試獲取的矩形箱振動發聲系統輻射聲功率級總值、6個遠場測點的聲壓級總值與上述兩種規模的等效面聲源預測值進行對比,并給出了相應的誤差,如表1所示.由表1可知:16個等效面聲源預測時,聲功率級相差2.7 dB(A),誤差2.8%,在誤差接受范圍內,6個遠場測點,最大預測誤差12.2%;70個等效面聲源預測,聲功率級相差0.4 dB(A),誤差僅0.4%,6個遠場測點,最大預測誤差3.1%.

3.3 氣動發聲系統等效面聲源預測

將小型離心風機與理想體積聲源放入矩形箱內,風機轉速約為1 200 r/min.作為氣動聲源,體積聲源頻率范圍100～1 000 Hz,體積加速度-0.5 m3/s2.經實驗測試獲取矩形箱氣動發聲系統近場表面區域的聲壓信息之后,建立等效面聲源的仿真模型,每一個等效面賦以相應位置測點的聲壓數據作為邊界條件,共同組成了矩形箱氣動發聲系統的等效聲源模型.數值計算時,在同樣的坐標位置設置測試輻射聲功率的6個場點,以計算等效聲源系統的輻射聲功率級.圖8給出了實驗測試的矩形箱氣動發聲系統輻射聲功率級與等效面聲源數值計算獲取的輻射聲功率級頻譜曲線,在整個頻率范圍內仿真值略微高于實驗值,整體上處于同一個噪聲水平.

表1 等效聲源預測與實驗值對比Tab.1 Results of equivalent sound model simulation and test

實驗測試矩形箱氣動發聲系統輻射聲功率級總值、6個遠場測點的聲壓級總值與等效面聲源預測值進行對比,并給出了相應的誤差,如表2所示.由表2可知：等效面聲源預測時,聲功率級相差1.4 dB(A),誤差1.64%,在誤差接受范圍內,6個遠場測點,聲壓級相差基本都在3 dB(A)以內,最大預測誤差9.46%.

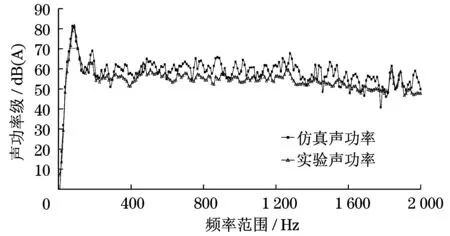
圖8 等效面聲源仿真結果Fig.8 Simulation results of equivalent sound model with seventy regions

表2 等效聲源預測與實驗值對比Tab.2 Results of equivalent sound model simulation and test

4 結語

本文提出了一種結構與空氣噪聲的等效面聲源預測方法,將振動或氣動發聲系統作為一個整體,建立一個虛擬的包絡面并劃分子區域,通過實驗測試獲取各子區域中心近場聲壓代替該子區域的聲壓,從而形成整個振動或氣動發聲系統的等效面聲源模型,并以之作為邊界條件,結合聲學邊界元方法預測該系統輻射聲功率和輻射聲場內任意點的聲壓,通過算例驗證了該方法的有效性和可行性.從預測準確度來講,當等效聲源面較少時,振動或氣動發聲系統的輻射聲功率級的預測能夠滿足工程應用精度要求,但輻射聲場的任意點聲壓的預測不盡如人意.為了獲取更高的預測準確度,可以適當增加等效聲源面,以在聲功率級與任意點聲壓預測時均獲得讓人滿意的結果.