下肢康復(fù)訓(xùn)練機器人協(xié)作控制與S型規(guī)劃算法研究

龔蘭芳,曹成濤,許倫輝

(1.廣東水利電力職業(yè)技術(shù)學院 自動化工程系，廣州 510925; 2.廣東交通職業(yè)技術(shù)學院 智能交通工程技術(shù)應(yīng)用中心,廣州 510650; 3.華南理工大學 土木與交通學院,廣州 510640)

一般來說,下肢康復(fù)訓(xùn)練機器人對指數(shù)積(Product of Exponentials,POE)運動控制、協(xié)作控制、軌跡規(guī)劃和超高速運動性能具有較高的要求[1-4].因此,對下肢康復(fù)機器人的運動學、動力學和軌跡規(guī)劃進行研究，是提升康復(fù)類下肢康復(fù)訓(xùn)練機器人靈活性和靈敏度的重要保證[5].下肢康復(fù)機器人步態(tài)訓(xùn)練有兩種主要方法:跑步機訓(xùn)練和可編程末端執(zhí)行器訓(xùn)練.

本文首先研究了下肢康復(fù)訓(xùn)練機器人的訓(xùn)練原理,然后建立了POE運動學模型和動力學辨識模型[5].針對簡化后的模型參數(shù)，采用最小二乘法辨識了動力學參數(shù),從而實現(xiàn)了協(xié)作控制.最后在前面研究的基礎(chǔ)上,提出了一種加加速度受限的非對稱S型軌跡規(guī)劃方法,給出了一種S型軌跡插補形狀的完整算法,對提升下肢康復(fù)系統(tǒng)啟動和停止速度、確保軌跡平滑等具有積極作用.與許多其他軌跡規(guī)劃技術(shù)不同,保證了機器人運動的運動學約束,表示為所有機器人關(guān)節(jié)的速度、加速度和抖動的絕對值的上限.通過系統(tǒng)實驗,驗證協(xié)作控制算法和位置伺服系統(tǒng)下S型軌跡插補規(guī)劃控制結(jié)果的正確性.

1 下肢康復(fù)機器人運動控制

圖1為所研究的下肢康復(fù)機器人,它在肢體修復(fù)過程中能夠通過編程方式加以控制,并且實現(xiàn)可變的預(yù)定步進姿勢和力感測[6-8].下肢康復(fù)機器人可以幫助患者模擬正常人的腳步,鍛煉腿部肌肉,逐漸恢復(fù)神經(jīng)控制,從而幫助患者完成行走動作,最終以正常方式完全行走.

圖1 柔性下肢康復(fù)機器人Fig.1 Flexible lower limb rehabilitation robot

1.1 POE正運動學

手臂運動學正解:串聯(lián)開鏈機器人的正向運動學公式,對于n個轉(zhuǎn)動/移動關(guān)節(jié)的串聯(lián)機器人來說,設(shè)base0為基坐標系,為Tooln+1為工具坐標系,則應(yīng)用POE公式計算機器人的正向運動學模型步驟如下:

步驟1計算機器人末端初始位姿

(1)

式中:Rst為姿態(tài)矩陣；Pst為剛體的位置矢量.

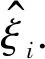
根據(jù)歐拉定理,任意一個三維空內(nèi)的旋轉(zhuǎn)運動都可以表示為圍繞著某一個軸ω的轉(zhuǎn)動,假設(shè)轉(zhuǎn)動角度表示為θ,那么可以將該旋轉(zhuǎn)矩陣表示為矩陣指數(shù)的形式,即

(2)

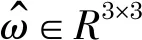
對于轉(zhuǎn)動關(guān)節(jié)來說，q為轉(zhuǎn)軸上任意一點的坐標,關(guān)節(jié)轉(zhuǎn)動對應(yīng)的運動旋量坐標表示為

則

對于移動關(guān)節(jié)來說,運動旋量中的ω對應(yīng)分量為0,即

步驟3代入POE公式

(3)

1.2 機器人動力學建模

對于任何機械系統(tǒng),拉格朗日函數(shù)L定義為系統(tǒng)的動能Ek和勢能Ep之差:

系統(tǒng)動力學方程(稱第二類拉格朗日方程)為

(4)

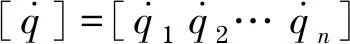
利用拉格朗日函數(shù)L,系統(tǒng)動力學方程可以表示為

由于勢能Ek不顯含速度項,因此，動力學方程也可以寫成

(5)

1.2.1拉格朗日動力學

拉格朗日(動能與位能法):m1,m2,m3分別表示3個桿件質(zhì)量,l1,l2,l3分別表示3個桿件長度,d1,d2,d3分別表示3個桿件質(zhì)心到關(guān)節(jié)的距離.

設(shè)關(guān)節(jié)1上升高度為h,3個旋轉(zhuǎn)關(guān)節(jié)旋轉(zhuǎn)角度分別為θ1,θ2,θ3,q1=θ1,q2=θ2,q3=θ3,則康復(fù)機器人在運動平面內(nèi)位置如圖2所示.

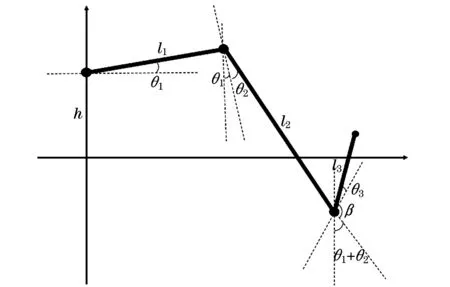
圖2 康復(fù)機器人在運動平面內(nèi)位置Fig.2 The position of a rehabilitative robot in the motion plane

1.2.2機器人總勢能和動能

康復(fù)機器人桿件1的勢能P1為

康復(fù)機器人桿件2的勢能P2為

康復(fù)機器人桿件3的勢能P3

則康復(fù)機器人總位能為

(6)

康復(fù)機器人連桿1的動能K1為

康復(fù)機器人連桿2的動能K2為

康復(fù)機器人連桿3的動能K3為

式中：J1，J2，J3分別為連桿1，2，3的轉(zhuǎn)動慣量.則康復(fù)機器人總動能為

(7)

1.2.3拉格朗日函數(shù)

拉格朗日函數(shù)L為

則康復(fù)機器人各關(guān)節(jié)驅(qū)動力矩為

式中:C1,C2,C3分別為3根連桿驅(qū)動電機的電勢系數(shù)；S1，S2，S3分別為第1，2，3個關(guān)節(jié)施轉(zhuǎn)角度的正弦值.

1.3 摩擦力矩擬合方法

根據(jù)對機器人的摩擦力矩Tf的測試,可以看出摩擦力矩的大小變化與機器人的重力矩、加速轉(zhuǎn)矩和轉(zhuǎn)動角速度的大小變化相關(guān).為了簡單的線性化擬合,試將摩擦力矩擬合公式確定如下:

(8)

計算角速度影響因數(shù)b,利用測量軟件測得Tf,消除將Tf中的重力矩,則

此時,Tf只有角速度和加速轉(zhuǎn)矩的影響,選取機器人平穩(wěn)運行的時間段,在角速度平穩(wěn)時進行影響因數(shù)b的擬合.

計算加速轉(zhuǎn)矩影響因數(shù)c,在重力矩和角速度影響因數(shù)確定完成之后,簡單運算即可求出加速轉(zhuǎn)矩影響因數(shù).

2 S型軌跡規(guī)劃

機器人技術(shù)的一個基本問題在于軌跡規(guī)劃,它可以這樣定義:找出沿給定幾何路徑的時間運動規(guī)律,軌跡差補規(guī)劃專用于為機器人的控制系統(tǒng)生成驅(qū)動器的參考輸入,以便電動機能夠執(zhí)行該運動.在軌跡差補中,運動學和動力學約束是軌跡規(guī)劃算法的輸入,而關(guān)節(jié)(或末端效應(yīng)器)的軌跡表示為位置、速度和加速度值的時間序列,是輸出.

步驟1V為S型速度曲線的速度,J為S型速度曲線的加加速度,P為所走的路程,t為系統(tǒng)獲得的機器人狀態(tài)的相應(yīng)時間序列.對于t0～t1

步驟2對于t1～t2

步驟3對于t2～t3

步驟4對于t3～t4

步驟5對于t4～t5

步驟6對于t5～t6

步驟7對于t6～t7

3 實驗結(jié)果及分析

3.1 協(xié)作控制算法驗證

本文在研發(fā)了柔性下肢康復(fù)機器人的動力學控制框架的基礎(chǔ)上,驗證軟件編寫的拉格朗日法的正確性.圖3是使用機器人平臺控制器展示協(xié)作控制算法,從圖3(a)和圖3(b)對比分析數(shù)據(jù)圖可知,在機器人零力控制即不受重力和摩擦力的條件下,寫作控制算法具有良好的效果,確實有效,從側(cè)面驗證了動力學算法和辨識出參數(shù)的準確性,可以有效地用到協(xié)作功能中去.

圖3 柔性下肢康復(fù)機器人負載零力控制Fig.3 Load zero force control of flexible lower limb rehabilitation robot

3.2 軌跡規(guī)劃實驗

從圖4可以看出S型軌跡規(guī)劃的正確性.在關(guān)節(jié)空間中而不是在操作空間中規(guī)劃軌跡具有一個主要優(yōu)點,即控制系統(tǒng)作用于操縱器而不是作用于末端作用器,所以在聯(lián)合工作空間內(nèi)更容易實現(xiàn)運動軌跡的調(diào)整.此外,關(guān)節(jié)空間的軌跡規(guī)劃可以避免由運動奇點和操縱引起的問題.但是,在關(guān)節(jié)空間中，進行軌跡規(guī)劃中,在關(guān)節(jié)與末端作用器連接過程中,引入的非線性操作將會影響末端效應(yīng)器動作執(zhí)行的可預(yù)見性.S型軌跡規(guī)劃要求伺服驅(qū)動通常采用位置控制,提高了電動機的速度和電流響應(yīng)速度,進而改善了位置控制的效果.

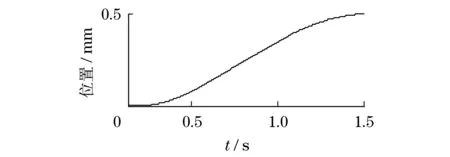
圖4 S型軌跡規(guī)劃Fig.4 S-shaped trajectory planning diagram

4 結(jié)語

本文以下肢康復(fù)機器人為研究對象,進行了分析.針對下肢康復(fù)機器人的結(jié)構(gòu)參數(shù)特點,首先運用POE運動控制求解了運動學問題,然后構(gòu)建了拉格朗日動力學方程,同時提出了一種摩擦力矩擬合的方法來構(gòu)建協(xié)作控制算法模型,最后討論了S型軌跡規(guī)劃的數(shù)學問題.規(guī)劃方法可以獲得較小的位置誤差和較低的系統(tǒng)振動,可以通過S型規(guī)劃插補產(chǎn)生平滑的軌跡,即具有良好的連續(xù)性特征的軌跡來實現(xiàn).經(jīng)過實驗證明運動學、動力學與S規(guī)劃算法對下肢康復(fù)機器人性能有很大的提升,同時對于機器人的精確運動控制有著重要的意義.下肢康復(fù)機器人初步實施被動者的被動動作和輔助動作,除了考慮運動模式,還要補充其他功能,下肢康復(fù)訓(xùn)練機器人將是一個更復(fù)雜的系統(tǒng).