3自由度柔性并聯機構自抗擾控制研究

周 微

(常州機電職業技術學院 機械工程學院,江蘇 常州 213164)

柔性并聯機構(Compliant Parallel Mechanism)是一種利用自身柔性桿件的彈性變形來傳遞運動的新型機構,通過有效地運用彈性變形來改善機構的運動特性,具有結構剛度強、無摩擦磨損、免裝配潤滑和運動精度高等優點,在生物醫學、高精度機床和機器人等領域有著廣泛的應用[1].由于柔性并聯機構的控制系統具有復雜多變量、強非線性和高耦合的特點,如何提高柔性并聯機構的軌跡跟蹤精度是控制研究急需解決的問題[2].文獻[3]從柔性并聯機構非線性與線性間的不確定性方面進行分析,基于H2/H∞混合魯棒控制,研究了機構的位置追蹤狀態.文獻[4]以一種柔性并聯機構為研究對象,采用合成法和PD相結合的控制方式,設計了一種基于機構動力學方程的新型控制器.文獻[5]采用一種結合應變速度和最佳狀態的反饋控制器,研究了平面3-RRR柔性并聯機構的殘余振動.文獻[6]采用Hensens & Kostic理論來補償柔性并聯機構的Lagrange方程,從而補償機構的單位定點誤差,分析了機構分別在S型、T型速度規劃算法下的位置和速度誤差.為了改善柔性并聯機構的位移軌跡跟蹤精度,本文基于3-PRR柔性并聯機構,設計了一種自抗擾控制器(Active Disturbance Rejection Control,ADRC),并分析了機構的位移追蹤誤差,有效提高了機構的控制穩定性.

1 3-PRR柔性并聯機構模型

1.1 機構模型

本文以3-PRR柔性并聯機構為研究對象,由于柔性并聯機構是以傳統的并聯機構為設計原型,并運用拓撲優化方法得到的一種新型機構,拓撲優化方法并沒有改變機構間的運動關系,故可以運用傳統3-PRR并聯機構的理論來分析3-PRR柔性并聯機構[7].

3-PRR柔性并聯機構有3個自由度,即沿XY方向的平移和繞Z方向的轉動,模型如圖1所示.機構由定平臺、動平臺以及連接動定平臺的3條對稱支鏈構成.機構的定平臺A1A2A3和動平臺C1C2C3均為等邊三角形,每條運動支鏈由1個移動副(P副)和2個轉動副(R副)構成.移動副連接著定平臺的各個頂點和轉動副,是機構的驅動副,驅動距離為di(i=1,2,3).連桿BiCi(i=1,2,3)長度均相等,兩端為轉動副且與動平臺相連.在動平臺的中心建立定坐標系O-xy,其中，θi為連桿BiCi與x軸正向的夾角,αi為AiBi與x軸正向的夾角,θP為動平臺C1C2C3繞z軸的旋轉角度.點P為動平臺的幾何中心,即機構的運動末端.

1.2 機構Jacobian分析

基于圖1的機構模型,采用閉環矢量法對機構的3條支鏈進行求解,可以得到支鏈的運動學約束關系，即

(1)

將式(1)的矢量方程投影至x軸和y軸,可得

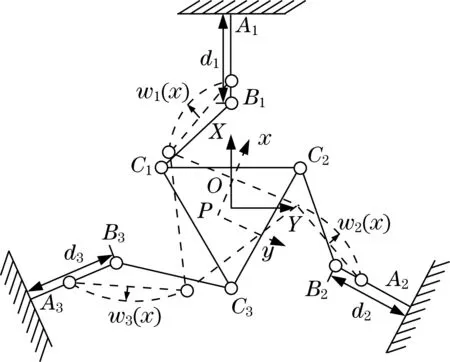
圖1 3-PRR柔性并聯機構模型Fig.1 Model of 3-PRR compliant parallel mechanism

(2)

式中:(xAi,yAi)為點Ai的坐標.

對式(2)求導,可得

(3)

2 系統控制器的設計

2.1 PID控制器的設計

PID控制是一種通過利用反饋誤差的方式來達到控制效果的閉環控制,是運用最廣泛的控制技術.PID控制器通過參數整定,調節比例、積分和微分3個參數值以形成控制器的理想輸出,這些參數的線性組合可以反映控制系統的響應速度和穩定性能[8].PID控制器的原理如圖2所示,其中，Integrator為積分器,Derivation為微分器.Kp,Ki,Kd3個參數的調節對于控制系統的效果有著關鍵作用,本文采用臨界曲線法來對Kp,Ki,Kd進行參數整定,使其達到最佳的控制效果.

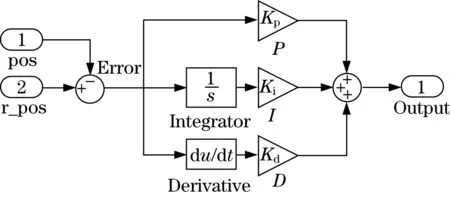
圖2 PID控制原理圖Fig.2 Schematic diagram of PID control

2.2 ADRC控制器的設計

ADRC主要由非線性跟蹤微分器、擴張狀態觀測器和非線性狀態誤差反饋3部分組成,原理如圖3所示.為了提高控制系統的動態特性,解決系統快速響應和超調間的矛盾,運用擴張狀態觀測器對被控對象進行實時在線估計,利用跟蹤微分器安排過渡過程,并對系統的總擾動進行補償.

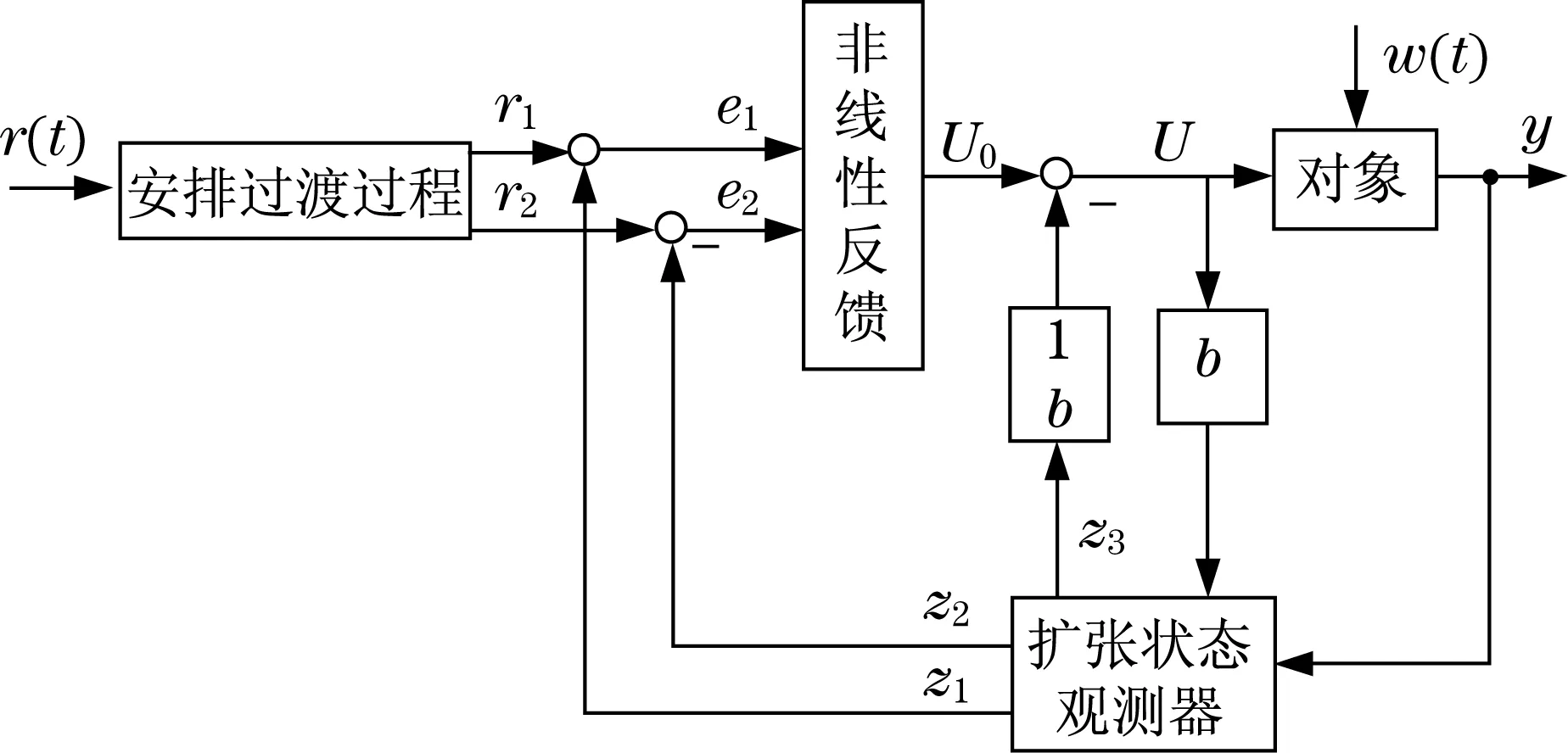
圖3 ADRC控制原理圖Fig.3 Schematic diagram of ADRC control

2.2.1 跟蹤微分器

跟蹤微分器是自抗擾控制的前饋通路部分,主要作用是處理系統的輸入信號r(k),并提取出輸入信號r(k)的跟蹤信號r1(k)和微分信號r2(k).跟蹤微分器可以根據輸入信號的大小和控制要求來安排過渡過程,解決快速響應和超調間的矛盾,使系統的輸入信號具有快速性且無超調的雙重特點.跟蹤微分器的輸出方程為

(4)

式中:h為系統采樣時間;r(k)為輸入信號.fst(x1,x2,δ,h0)為非線性函數,

(5)

式中:δ為速度因子,決定系統的跟蹤速度;h0為濾波因子,對噪聲進行濾波處理;sgn(·)為符號函數;d與α的值為

d=δh0

d0=h0d

y=x1+h0x2

(6)

(7)

2.2.2 擴張狀態觀測器

擴張狀態觀測器是自抗擾控制的反饋通路部分,主要作用是將系統未建模部分、內部參數攝動以及外界干擾等因素歸為一個新的狀態,為系統提供新的反饋輸入信號z(k)、擴張狀態變量和各階狀態變量.通過擴張狀態變量估算系統的干擾,從而利用反饋來補償系統擾動.擴張狀態觀測器的輸出方程為

(8)

式中:y(k)為系統輸出信號;u(k)為系統非線性狀態反饋輸出信號;ε0為初始輸出誤差信號;z1(k),z2(k),z3(k)分別為跟蹤信號、微分信號和反饋誤差信號;b0,β1,β2,β3為控制參數;fal(ε0,αi,δ0)為非線性函數,

(9)

式中:δ0為初始速度因子;ε為輸出誤差信號;αi為實數,0<αi<1.

2.2.3 非線性狀態誤差反饋

由于PID控制律的Kp,Ki,Kd線性組合往往會造成控制系統快速響應與超調之間的矛盾,因此，非線性狀態誤差反饋將Kp,Ki,Kd的線性組合轉變為非線性組合,從而實現自抗擾控制.非線性狀態誤差反饋的控制律方程如下:

e1(k)=r1(t)-z1(k)

e2(k)=r2(t)-z2(k)

u0=kpfal(e1,α01,δ1)+kdfal(e2,α02,δ1)

(10)

式中:kP,kd為非線性狀態反饋的比例和微分參數;e1(k),e2(k)分別為跟蹤誤差信號和微分誤差信號;fal(e2,α02,δ1)與式(9)相同,0<α01<α02<1.

2.3 ADRC控制器穩定性分析

假設系統為不確定參數2階系統,ei=xi-zi(i=1,2,3),那么可得到系統的偏差狀態方程為

(11)

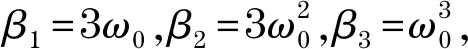
(12)

由式(12)可知,參數ω0決定了擴張觀測器的控制性能,且偏差狀態方程的3個極點都處于同一位置,此時有

(13)

由于fal(e1,a01,δ)為奇函數,當kp>0時,P(e1)>0.因此，控制器方程可簡化為

(14)

系統的平衡點為e1=e2=0.

選取Lyapunov函數為

(15)

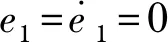
(16)

因此，控制系統處于半負定,符合Lyapunov穩定性的要求[9].

3 控制仿真

根據柔性并聯機構的結構特性,不斷調節控制器的參數,直至機構運動平穩且誤差波動較小,仿真時間為10 s.PID控制器的控制參數Kp=8.5,Ki=0.5,Kd=0.2.ADRC控制器的參數為δ=6,α1=0.3,α2=0.1,β1=51,β2=372,β3=1 058,δ0=0.004,kp=18,kd=0.9,α01=0.6,α02=0.8,δ1=0.05.系統在X,Y,Z3個方向的PID控制和ADRC控制位移跟蹤曲線分別如圖4～圖6所示.

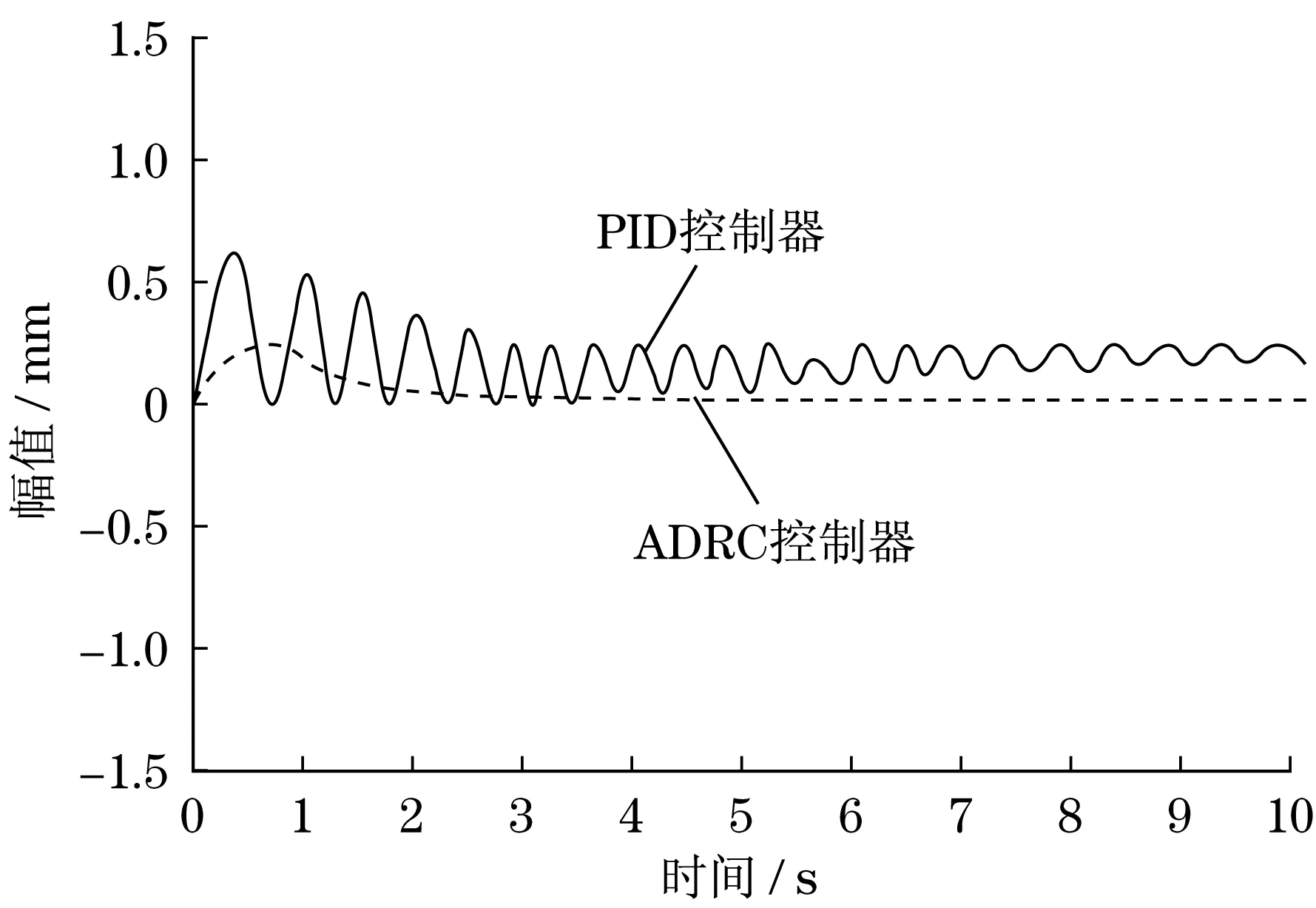
圖4 X方向位移跟蹤誤差曲線Fig.4 Displacement tracking error curve of X-direction

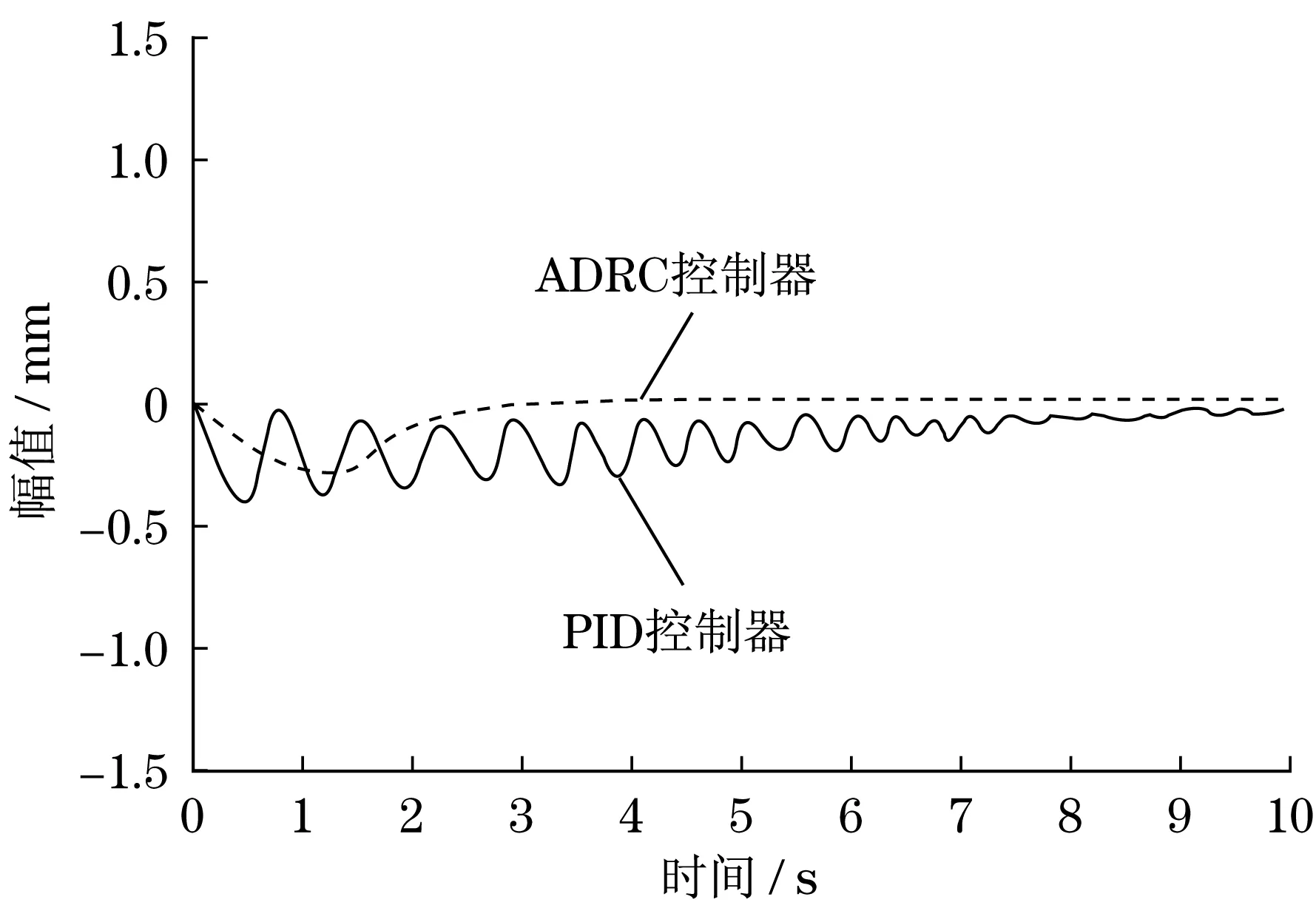
圖5 Y方向位移跟蹤誤差曲線Fig.5 Displacement tracking error curve of Y-direction

由圖4～圖6可知：PID控制和ADRC控制在最初的3 s時間內,均存在較大的軌跡跟蹤誤差,軌跡跟蹤的穩定性較差.經過一段控制算法的實時運算,兩種控制方式都能達到一定的控制精度,但是隨著ADRC控制不斷消除快速響應與超量間的矛盾,使得機構3個方向的軌跡跟蹤誤差逐漸趨近于零,而PID控制無法消除該矛盾,軌跡跟蹤誤差還是較大.由表1可知,與PID控制相比,ADRC控制的超調量和調整時間都更短,說明ADRC控制的穩定性更好,在響應速度方面更優.

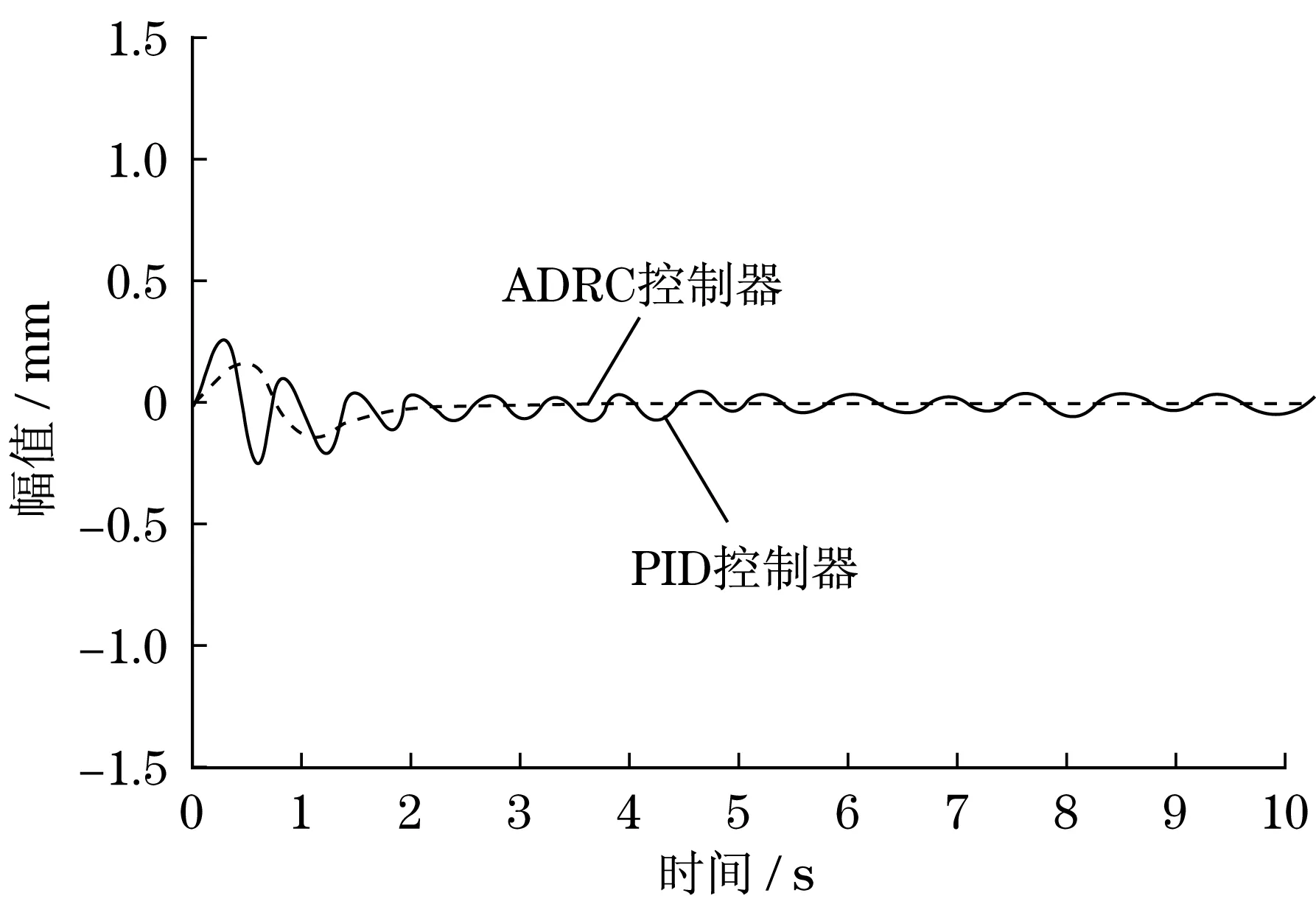
圖6 Z方向位移跟蹤誤差曲線Fig.6 Displacement tracking error curve of Z-direction

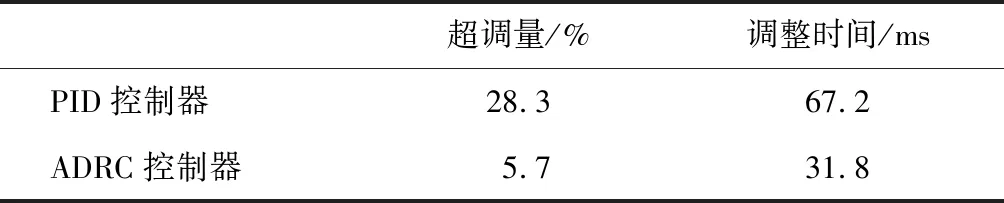
表1 仿真結果Tab.1 Simulation result

4 結語

基于3-PRR柔性并聯機構模型,根據閉環矢量法分析了機構的運動學方程,得到的輸入輸出Jacobian矩陣為控制系統提供了參考輸入.分別設計了PID控制器和ADRC控制器,并分析了ADRC控制器的非線性跟蹤微分器、擴張狀態觀測器和非線性狀態誤差反饋部分.研究了柔性并聯機構在PID控制和ADRC控制兩種不同控制方式下的位移軌跡誤差曲線,結果表明:ADRC控制可以解決快速響應與超調間的矛盾,軌跡跟蹤誤差小,響應速度快,可以滿足柔性并聯機構高追蹤精度的要求.