采用改進粒子群算法的優化電液無凸輪氣門機構控制研究
白 潔,王 勝
(1.吉林電子信息職業技術學院 汽車工程學院,吉林 吉林 132021; 2.燕山大學 機械工程學院,河北 秦皇島 066044)
發動機性能評價指標包括氣門升程、開啟相位和持續時間等,改善氣門設計機構是提高發動機熱效率和減少有害氣體排放的重要措施.傳統氣門驅動大多采用凸輪機構,由于凸輪機構型線固定,不能在驅動過程中進行調整,因此,凸輪驅動氣門機構很難滿足不同工況下都達到最優.為了更好地發揮發動機工作性能,采用無凸輪液壓驅動機構,從而實現了氣門機構的在線調整.與傳統凸輪驅動機構相比,液壓可變氣門機構具有以下優點[1-2]:① 發動機在不同轉速條件下,氣門開啟速度和流通截面積較好;② 改變液壓流量就可以改變氣門開啟速度;③ 能夠實現氣門正時的連續可變.因此,研究無凸輪液壓驅動氣門機構,對提高發動機性能具有重要意義.
隨著汽車技術的改進,其發動機性能要求也隨之提高.因此,許多學者對發動機氣門機構控制方法展開了研究.例如:文獻[3]研究了無凸輪配氣機構的設計方法,分析了氣門升程曲線特性,建立液壓驅動控制方法,給出了液壓驅動方程式,采用氣門軟著落方案,通過液壓驅動柔性調節無凸輪配氣機構,從而降低了氣門落座的沖擊力.文獻[4]研究了氣門機構全可變液壓驅動控制方法,建立氣門運動試驗平臺,采用氣門落座緩沖機構控制氣門落座速度,通過位移傳感器測量氣門升程,試驗結果表明,氣門落座緩沖機構有效地降低氣門落座的速度和高度.文獻[5]研究了電控氣動發動機氣門開啟時刻的控制方法,分析了發動機進氣門開啟角的控制規律,建立氣缸內氣體狀態模型,通過實驗驗證工況變化對進氣門開啟角度的影響,得到了發動機最佳進氣門開啟角的變化規律.但是,氣門在打開和關閉過程中,由于突然發生變化,導致氣門升程和速度誤差較大.對此,建立電液氣門機構簡圖模型,給出活塞運動壓力方程式.采用神經網絡控制電液伺服閥,引用改進粒子群算法優化神經網絡控制器,給出氣門控制在線優化流程圖.采用數學軟件Matlab對氣門升程和速度誤差進行仿真驗證,并與神經網絡控制誤差進行比較,為提高氣門運動精度提供參考.
1 電液氣門機構
本文采用的電液無凸輪氣門機構主要包括控制模塊、驅動模塊和執行模塊3個部分,如圖1所示.控制模塊采用神經網絡控制伺服閥油液的流動方向,從而實現活塞的上、下運動;驅動模塊主要為伺服閥控制提供動力;執行模塊通過活塞的上、下運動,從而實現氣門的打開和關閉.
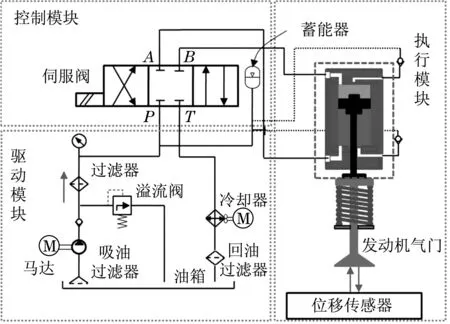
圖1 電液無凸輪氣門機構Fig.1 Electro hydraulic cam less valve mechanism
驅動活塞運動的壓力大小主要由供油壓力和伺服閥控制信號決定.油液非線性動力學數學模型計算復雜,為了簡化計算過程,建立線性數學模型求解壓力,其計算方程式[6]如下:
(1)
式中:M為氣門機構質量;x為氣門位移;B為阻尼系數;T為油液溫度;D為氣門孔直徑;K為彈簧剛度;Fac為活塞驅動力.
根據牛頓定律,可以推導活塞驅動力的方程式為
(2)
式中:A1為活塞無桿端面積;A2為活塞有桿端面積;p1為活塞無桿端控制腔壓力;p2為活塞有桿端壓力;Bv為油液阻尼系數.
活塞兩端面積求解方程式為
(3)
式中:Dp為活塞直徑;Ds為活塞連桿直徑.
油液阻尼系數求解方程式為
(4)
式中:μ為油液動態黏度;Kc為彈性剛度;As為活塞摩擦面積;c為活塞與液壓缸垂直方向間隙.
活塞摩擦面積求解方程式為
(5)
式中:l為活塞連桿運動距離.
2 改進神經網絡控制器
2.1 徑向基函數神經網絡
徑向基函數神經網絡結構主要包含3個部分:① 輸入層;② 隱含層;③ 輸出層.神經網絡結構如圖2所示.它能夠逼近任意非線性函數,具有良好的泛化能力,并且有很快的收斂速度.
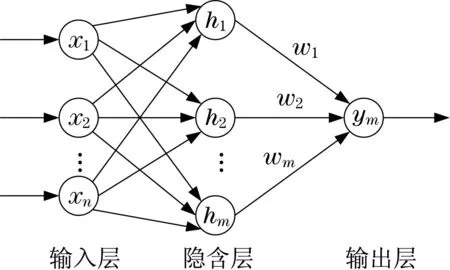
圖2 神經網絡結構Fig.2 Neural network structure
在神經網絡控制結構中,隱含層函數[7]采用高斯基函數,即
(6)
式中:X=[x1,x2,…,xn]T為神經網絡輸入層向量;cj=[cj1,cj2,…,cjn]為隱含層節點j的中心矢量;bj為隱含層節點j的基函數寬度.
徑向基函數神經網絡輸出層函數[7]為
(7)
式中:W=[w1,w2,…,wm]T為神經網絡調節權值向量;H=[h1,h2,…,hm]T為神經網絡徑向基向量.
神經網絡控制器輸出誤差函數為
(8)
式中:y(t)為系統理論輸入信號;ym(t)為系統實際輸出信號.
神經網絡控制器各參數迭代算法[7]如下:
wj(t)=wj(t-1)+η[y(t)-ym(t)]hj+
α[wj(t-1)-wj(t-2)]
(9)
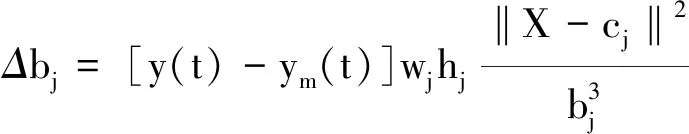
(10)
bj(t)=bj(t-1)+ηΔbj+
α[bj(t-1)-bj(t-2)]
(11)
(12)
cji(t)=cji(t-1)+ηΔcji+
α[cji(t-1)-cji(t-2)]
(13)
式中:η為學習速率;α為動量因子.
采用雙神經網絡控制電液伺服驅動,一個神經網絡進行在線辨識,另外一個網絡作為控制器,神經網絡各個調節參數會影響到控制輸出誤差,因此,需要對各個參數進行在線優化.
2.2 改進神經網絡控制器
粒子群算法(Particle Swarm Optimization,PSO)是一種啟發式全局優化算法,通過模仿動物群體覓食不斷迭代搜索最優值[8].在迭代搜索最優值過程中,粒子對比個體最優值和全局最優值后,決定是否更新粒子速度和位置.粒子速度和位置迭代方程式[9-10]為
式中:vi(k+1)為種群粒子i迭代(k+1)次的速度;vi(k)為種群粒子i迭代k次的速度;ω為慣性權值;xi(k+1)為種群粒子i迭代(k+1)次的位置;xi(k)為種群粒子i迭代k次的位置;c1和c2為區間[0,2]的學習因子;r1和r2為區間[0,1]的隨機數;Pi為種群粒子i的個體最佳位置;G為種群最佳位置.
慣性權值影響到局部搜索和全局搜索能力,為了更好地搜索全局最優值,慣性權值需要進一步修正,其方程式[11]為
(16)
式中:ω0為初始慣性權值;ω1為最終慣性權值;t為當前迭代次數;T為最大迭代次數.
電液無凸輪氣門機構采用的改進粒子群算法優化神經網絡控制流程如圖3所示.
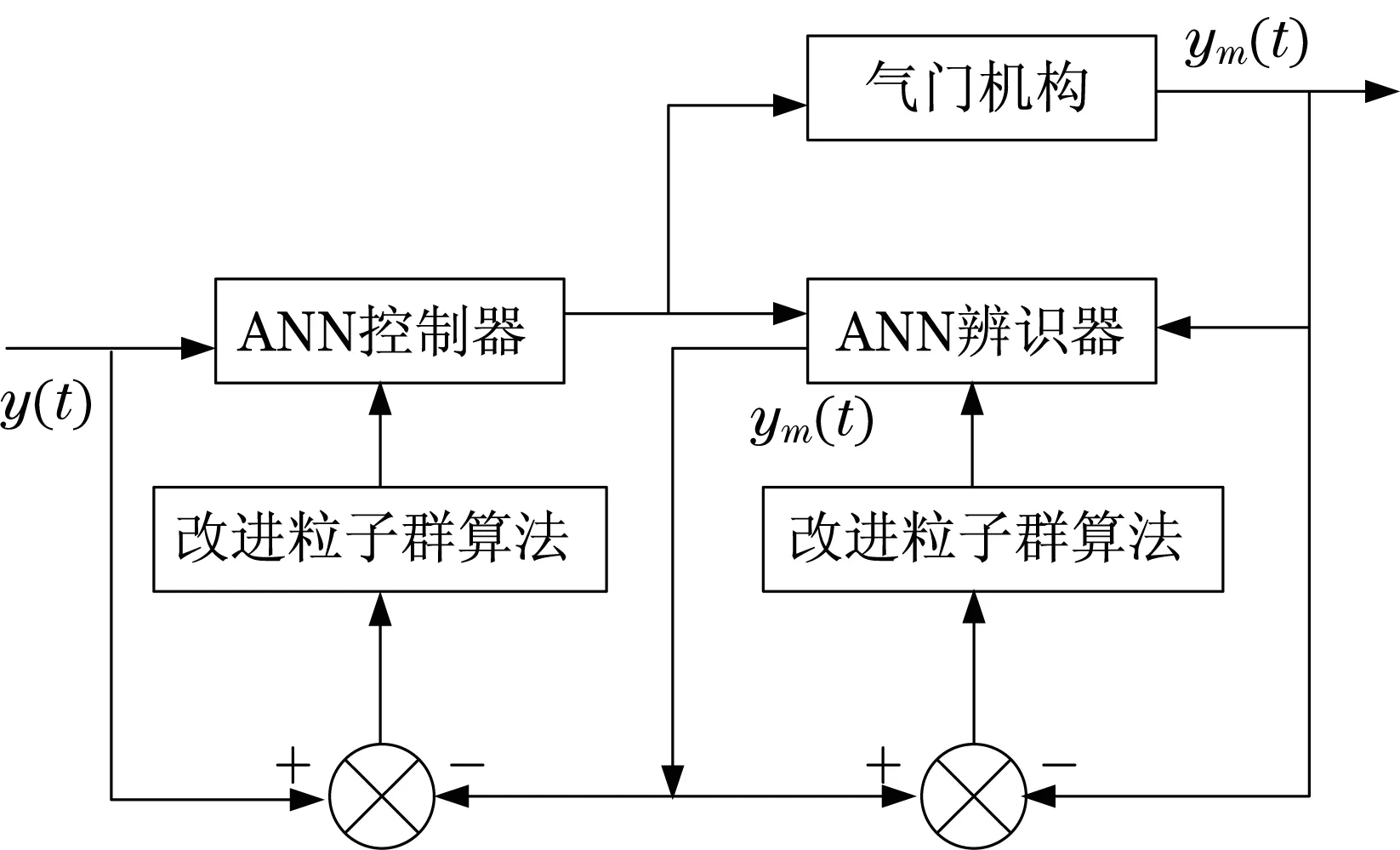
圖3 氣門機構控制流程Fig.3 Valve control flow
3 誤差仿真及分析
為了驗證電液無凸輪氣門機構采用改進神經網絡優化后的控制效果,采用Matlab軟件對氣門運動誤差進行仿真,仿真參數設置如下:種群大小為N=100,最大迭代次數為T=300,學習因子為c1=c2=1,隨機數為r1=r2=1,初始慣性權值ω0=0.8,最終慣性權值ω1=0.3,學習速率η=0.35;動量因子α=0.05.假設氣門升程曲線采用正弦曲線y=[8sin(2πt)] mm,氣門升程、速度跟蹤誤差分別如圖4和圖5所示.
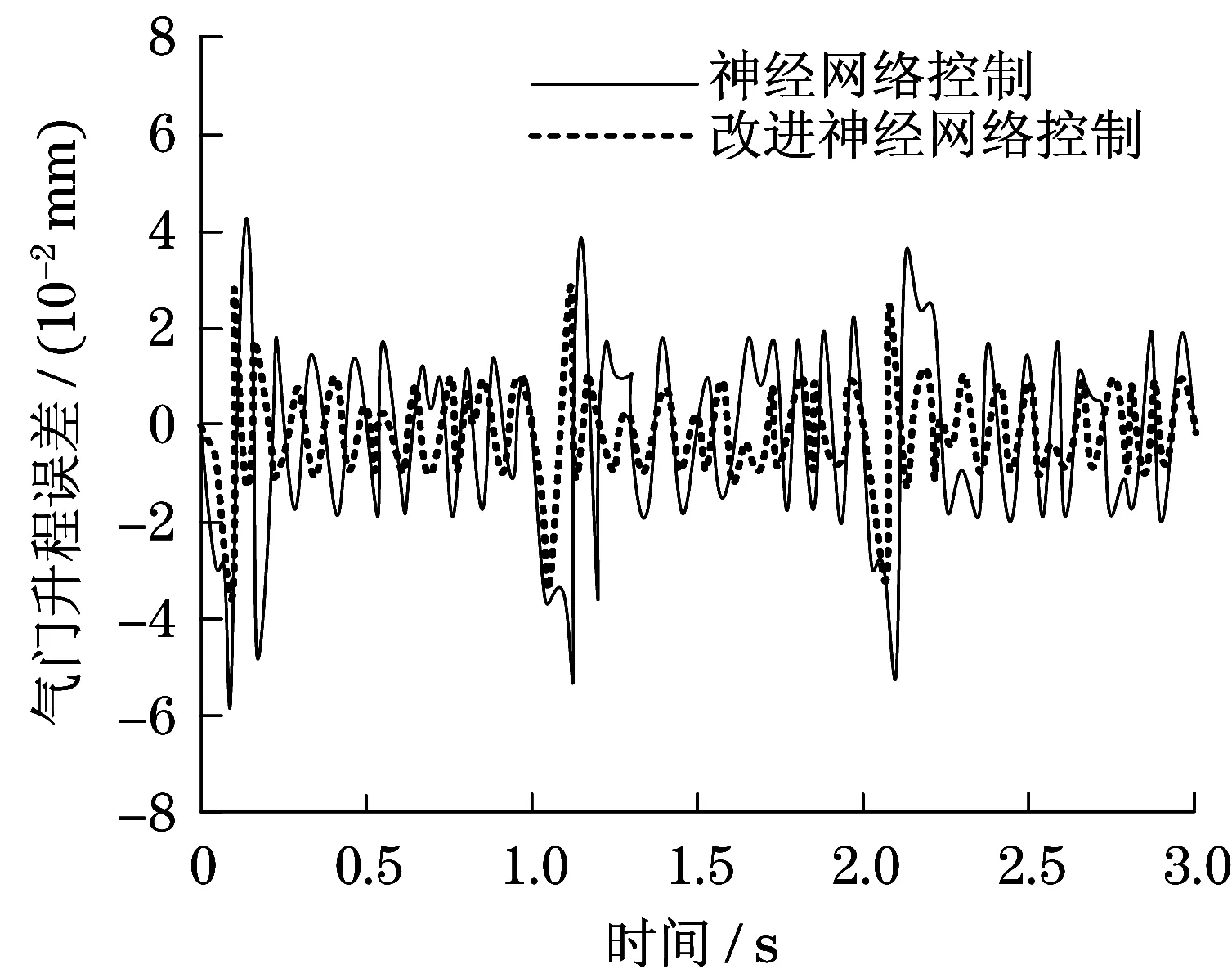
圖4 氣門升程誤差Fig.4 Valve lift error

圖5 氣門速度誤差Fig.5 Valve speed error
比較圖4誤差可得,采用神經網絡控制器,氣門升程跟蹤誤差最大值為5.8×10-2mm,采用改進粒子群算法優化神經網絡控制器,氣門升程跟蹤誤差最大值為3.5×10-2mm,氣門升程最大誤差降低了39.7%.比較圖5誤差可得,采用神經網絡控制器,氣門運動速度跟蹤誤差最大值為8.7×10-2mm·s2,采用改進粒子群算法優化神經網絡控制器,氣門運動速度跟蹤誤差最大值為4.8×10-2mm·s2,氣門速度最大誤差降低了44.8%.因此,采用改進粒子群算法優化神經網絡控制器,在氣門升程的情況下,能夠提高氣門升程運動軌跡跟蹤精度.
4 結論
針對電液無凸輪氣門升程運動軌跡與理論誤差較大問題,采用改進粒子群算法優化神經網絡控制器,并對控制誤差仿真驗證,主要結論如下:① 電液無凸輪氣門升程采用神經網絡控制方法,升程跟蹤誤差較大,而采用改進粒子群算法優化神經網絡控制器,升程跟蹤誤差較小.② 電液無凸輪氣門升程運動速度采用神經網絡控制方法,運動速度誤差較大,導致振動幅度較大,設計過程中應該盡量避免.③ 神經網絡控制器采用改進粒子群算法優化后,其反應速度快,能夠提高控制器穩定性,適用于電液無凸輪氣門控制方法.

