利用研究性學習 提升學習能力
——“豎直平面圓周運動”專題的研究案例分析

■郭 磊

研究性學習是全面培養學生綜合運用所學知識的能力、收集和處理信息的能力、分析和解決問題的能力、語言文字能力，以及團結協作能力的重要環節。這種方法還有利于培養學生獨立思考的習慣，激發學生的創新意識。

在高三的專題復習過程中，對于“豎直平面圓周運動”這個知識點，同學們可以先在小組合作中突破重難點，在大家都參與的知識點的生成過程中，弄清怎么把多個知識點整合到一起。具體做法是先圍繞本專題所要解決的問題去挖掘一些問題并進行研究、探討，對存在障礙的問題應及時解決，通過小組內成員的共同努力和協作，將所提出的問題一個個解決;再將問題的結果進行歸納和總結，完成這個專題的復習目標。下面將這個專題中的一個知識點的復習過程展示如下。

專題內容：豎直平面內圓周運動的臨界問題。

模型設計：三大模型，即繩球模型、桿球模型、管道模型。

特殊位置：豎直平面內圓周運動的最高點和最低點。

知識儲備：分別根據三大模型的特點，畫出小球在最高點和最低點的受力示意圖，并結合受力示意圖，寫出向心力的關系式。注意兩個問題，一是桿球模型和管道模型中，小球在最高點的受力情況分成兩種情況;二是小球在最高點和最低點這兩個特殊位置時，小球速度大小的關系，動能定理的使用。

圖1

問題一：如圖1所示，長為L的輕桿一端固定著一質量為m的小球，使小球在豎直面內做圓周運動。

(1)當小球在最高點B的速度為v1時，求輕桿對小球的作用力。

(2)輕桿拉小球過最高點的最小速度為多少?

(3)試分析光滑圓管豎直軌道中，小球過最高點時受管壁的作用力與速度的關系。

解：(1)設輕桿對球的作用力向下，則。當v1=時，F=0;當時，F＞0，表示小球受到輕桿的作用力方向向下，表現為拉力;當時，F＜0，表示小球受到輕桿的作用力方向向上，表現為支持力。

(2)由(1)中的分析可知，輕桿拉小球過最高點的最小速度為零。

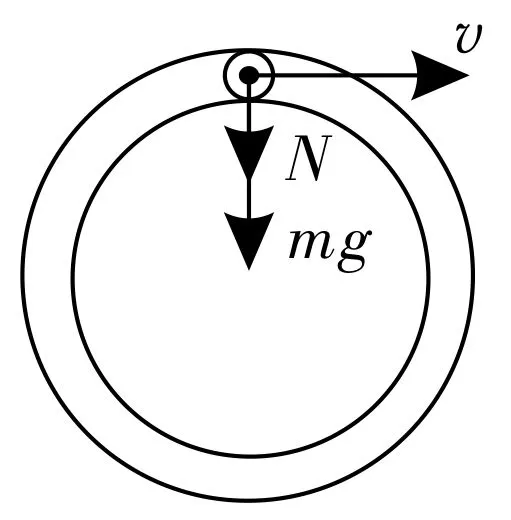
圖2

(3)如圖2所示，設管壁對小球的作用力向下，為N，則，得N=。當時，N＞0，即上管壁對小球有向下的壓力;當時，N＜0，即N豎直向上，下管壁對小球有向上的支持力。

【總結】細桿和管形軌道模型：

1.最高點的最小速度。

如圖3所示，細桿上固定的小球和管形軌道內運動的小球，因為桿和管在最高處能對小球產生向上的支持力，所以小球恰能到達最高點的最小速度v=0，此時小球受到的支持力N=mg。

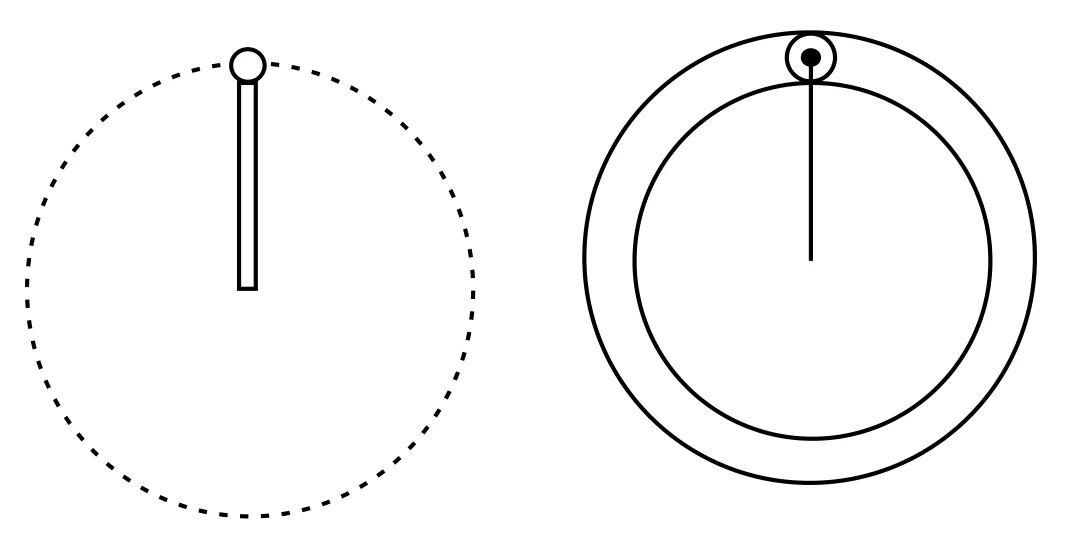
圖3

2.小球通過最高點時，細桿或管形軌道對小球的彈力情況。

(1)桿或管的外側對小球產生向下的拉力或彈力時，F隨v的增大而增大。

(2)小球在最高點只受重力時，不受桿或管的作用力，即F=0。

(3)桿或管的內側對小球產生向上的彈力時，F隨v的增大而減小。

3.小球能過最高點的條件：v≥0。

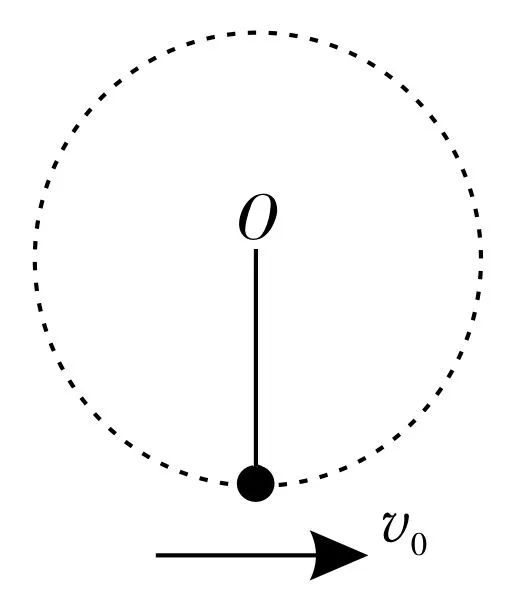
圖4

問題二：如圖4所示，一擺長為r的單擺，擺球的質量為m，要使擺球能在豎直平面內做完整的圓周運動，那么擺球在最低點的速度v0至少為多大?

圖5

解：小球在最高點受重力mg和繩的拉力T，如圖5所示，由牛頓第二定律得，因為m、r一定，所以v越小，T也越小。當T=0時。

討論：(1)如果把題中的擺繩去掉而改為與半徑與擺長相同的圓環，使小球沿環內側做圓周運動，那么情況又如何?

(2)如果在(1)的基礎上，使小球不脫離圓環軌道運動，則小球在最低點的最小速度為多少?

分析：若將繩變成圓環，在圓環的最高點，因為小球是沿環內側運動，環給小球提供支持力的方向是豎直向下的，和原題中繩在最高點的拉力情況一致，所以解決過程和原題是一致的。

在討論(2)中，同學們在理解小球不脫離圓環軌道這一要求時，容易只考慮小球做完整的圓周運動這一種情況，而忽略當小球運動到和圓心位置等高的點，速度減為零時，將不會繼續向上運動，而是沿圓環軌道滑下的情況。