全國(guó)名校導(dǎo)數(shù)綜合測(cè)試卷（B卷）答案與提示

1.A 2.C 3.B 4.D 5.A 6.C 7.B 8.B 9.B 10.D 11.A 12.B 13.y=2x+1。 14.

①若a≥0,當(dāng)0＜x＜1時(shí),f'(x)＞0,f(x)單調(diào)遞增;當(dāng)x＞1時(shí),f'(x)＜0,f(x)單調(diào)遞減。所以x=1是f(x)的極大值點(diǎn)。

②若a＜0,由f'(x)=0,得x=1或x=因?yàn)閤=1是f(x)的極大值點(diǎn),所以,解得-1＜a＜0。

綜合①②,a的取值范圍是(-1,+∞)。

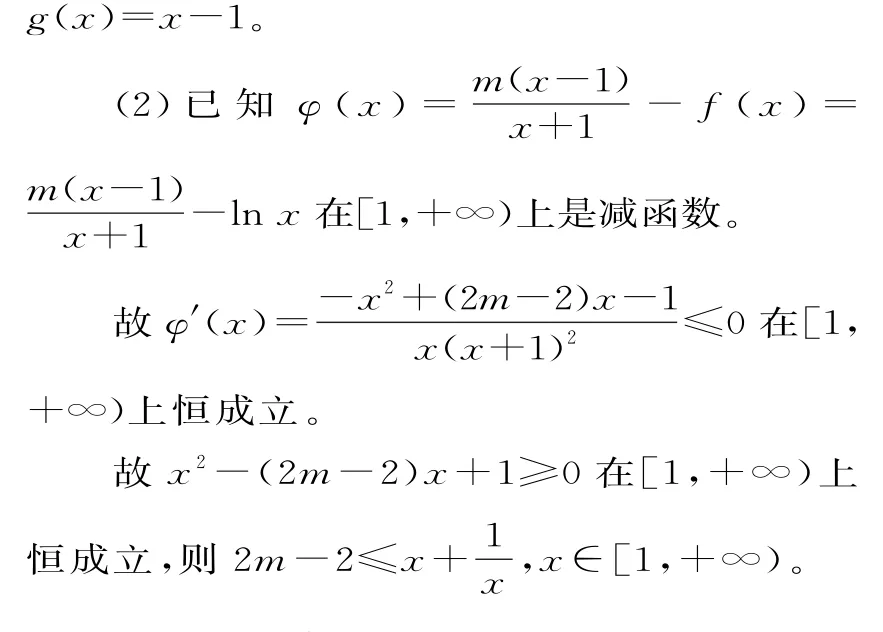
18.(1)當(dāng)a=2時(shí),f(x)=2lnx-x2+2x,f'(x)=-2x+2,切點(diǎn)坐標(biāo)為(1,1),切線的斜率k=f'(1)=2,則切線方程為y-1=2(x-1),即y=2x-1。

(2)g(x)=2lnx-x2+m,則g'(x)=

當(dāng)1＜x＜e時(shí),g'(x)＜0。

故g(x)在x=1處取得極大值,g(1)=m-1。

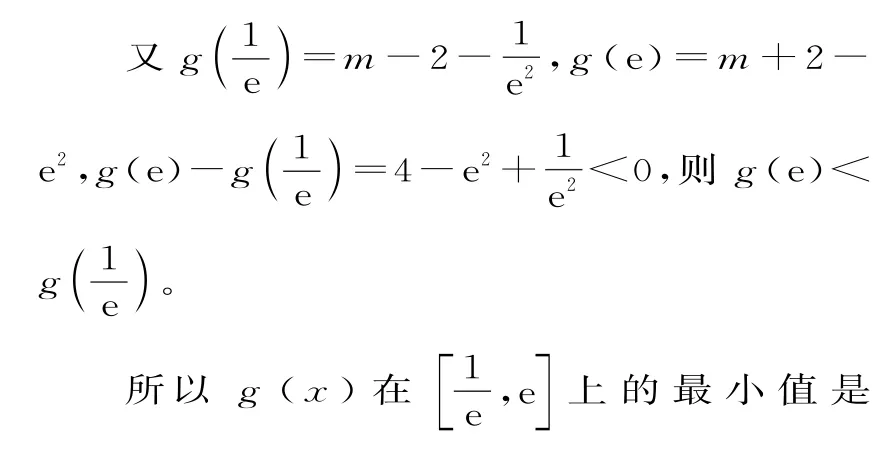
將x=40,y=500代入,得k=500e40。

故該產(chǎn)品一年的銷售量y(萬(wàn)件)關(guān)于x(元)的函數(shù)關(guān)系式為y=500e40-x。

所以L(x)=(x-30-a)y=500(x-30-a)e40-x(35≤x≤41)。

(2)由(1)得,L'(x)=500[e40-x-(x-30-a)e40-x]=500e40-x(31+a-x)。

①當(dāng)2≤a≤4時(shí),L'(x)≤500e40-x(31+4-35)=0,當(dāng)且僅當(dāng)a=4,x=35 時(shí)取等號(hào)。

所以L(x)在[35,41]上單調(diào)遞減。

因此,L(x)max=L(35)=500(5-a)e5。

②當(dāng)4＜a≤5 時(shí),L'(x)＞0?35≤x＜31+a,L'(x)＜0?31+a＜x≤41。

所以L(x)在[35,31+a)上單調(diào)遞增,在[31+a,41]上單調(diào)遞減。

因此,L(x)max=L(31+a)=500e9-a。

綜上所述,當(dāng)2≤a≤4時(shí),每件產(chǎn)品的售價(jià)為35元,該產(chǎn)品一年的利潤(rùn)L(x)最大,最大利潤(rùn)為500(5-a)e5萬(wàn)元;

當(dāng)4＜a≤5時(shí),每件產(chǎn)品的售價(jià)為(31+a)元時(shí),該產(chǎn)品一年的利潤(rùn)L(x)最大,最大利潤(rùn)為500e9-a萬(wàn)元。

20.(1)函數(shù)f(x)定義域?yàn)?0,+∞),

假設(shè)存在實(shí)數(shù)a,使f(x)在x=1 處取極值,則f'(1)=0,a=2。

此時(shí),f'(x)=,當(dāng)x＞0 時(shí),f'(x)≥0 恒成立,f(x)在(0,+∞)上單調(diào)遞增,故x=1不是f(x)的極值點(diǎn)。

故不存在實(shí)數(shù)a,使得f(x)在x=1 處取得極值。

(2)由f(x0)≤g(x0),得：

(x0-lnx0)a≥x20-2x0。

記F(x)=x-lnx(x＞0),則F'(x)=

當(dāng)0＜x＜1時(shí),F'(x)＜0,單調(diào)遞減;

當(dāng)x＞1時(shí),F'(x)＞0,單調(diào)遞增。

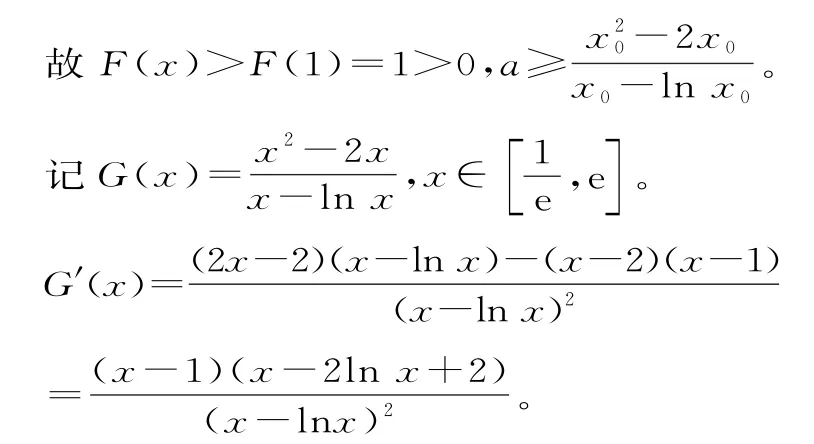
因此,實(shí)數(shù)a的取值范圍為[-1,+∞)。

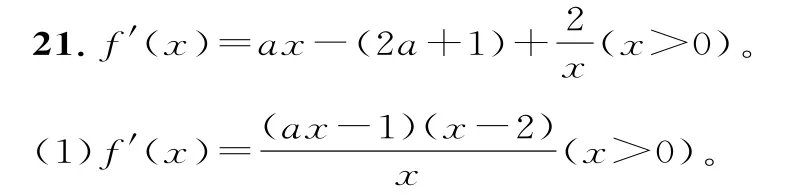
①當(dāng)a≤0 時(shí),x＞0,ax-1＜0,在區(qū)間(0,2)上,f'(x)＞0,在區(qū)間(2,+∞)上f'(x)＜0,故f(x)的單調(diào)遞增區(qū)間是(0,2),單調(diào)遞減區(qū)間是(2,+∞)。

綜上,a的取值范圍為(ln 2-1,+∞)。

22.(1)a=1時(shí),f(x)=(x2+x-1)ex,所以f'(x)=(2x+1)ex+(x2+x-1)ex=(x2+3x)ex。

曲線f(x)在點(diǎn)(1,f(1))處的切線斜率為k=f'(1)=4e。

又因?yàn)閒(1)=e,所以所求切線方程為y-e=4e(x-1),即4ex-y-3e=0。

(2)f'(x)=(2ax+1)ex+(ax2+x-1)·ex=[ax2+(2a+1)x]ex。

(3)當(dāng)a=-1時(shí),f(x)=(-x2+x-1)·ex,由(2)知,f(x)=(-x2+x-1)ex在(-∞,-1]上單調(diào)遞減,在[-1,0]上單調(diào)遞增,在[0,+∞)上單調(diào)遞減。

所以f(x)在x= -1 處取極小值,,在x=0處取極大值,f(0)=-1。

所以g(x)在(-∞,-1]上單調(diào)遞增,在[-1,0]上單調(diào)遞減,在[0,+∞)上單調(diào)遞增。故g(x)在x=-1處取得極大值g(-1),在x=0處取得極小值g(0)=m。

因?yàn)楹瘮?shù)f(x)與函數(shù)g(x)的圖像有3個(gè)不同的交點(diǎn),所以