如何破解導(dǎo)數(shù)中的隱零點問題

■河北省張家口市二中

導(dǎo)數(shù)中的隱零點問題多見于通過多次求導(dǎo),判斷導(dǎo)函數(shù)的正負(fù),確定原函數(shù)的單調(diào)區(qū)間,從而確定原函數(shù)的最值,或者求出參數(shù)的取值范圍。同學(xué)們雖然零點求不出來,但是找到零點滿足的方程、滿足的關(guān)系式,經(jīng)過變形,代入新構(gòu)造的函數(shù)中,可通過消元、換元以及降次達(dá)到解題的目的。

例1設(shè)函數(shù)f(x)=lnx-x,g(x)=xex-2x-1,證明：當(dāng)x＞0 時,g(x)≥f(x)。

證明：令F(x)=g(x)-f(x)=xexlnx-x-1(x＞0)。

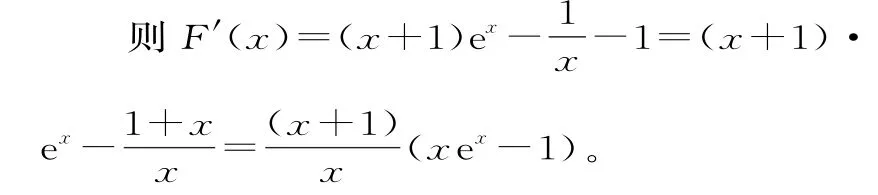
令G(x)=xex-1,則當(dāng)x＞0時,G'(x)=(x+1)ex＞0,函數(shù)G(x)在(0,+∞)上單調(diào)遞增。因為G(0)=-1,G(1)=e-1＞0,所以G(x)存在唯一的零點c∈(0,1)。且當(dāng)x∈(0,c)時,G(x)＜0;當(dāng)x∈(c,+∞)時,G(x)＞0。

故當(dāng)x∈(0,c)時,F'(x)＜0;當(dāng)x∈(c,+∞)時,F'(x)＞0。

F(x)在(0,c)上單調(diào)遞減,在(c,+∞)上單調(diào)遞增,從而F(x)≥F(c)=cec-

由G(c)=0,得cec-1=0,cec=1。

兩邊取對數(shù)得,lnc+c=0。F(c)=(cec-1)-(lnc+c)=0,F(x)≥F(c)=0,故g(x)≥f(x)。

注意：G(c)=0,cec-1=0的應(yīng)用。

例2設(shè)函數(shù)f(x)=xlnx-x2+2-x(a∈R),k∈N,g(x)=2-2x-x2,且當(dāng)x＞2時不等式k(x-2)+g(x)＜f(x)恒成立,試求k的最大值。

解析：由已知k(x-2)+g(x)＜f(x),可得k(x-2)+2-2x-x2＜xlnx-x2+2-x,也即k(x-2)＜xlnx+x。

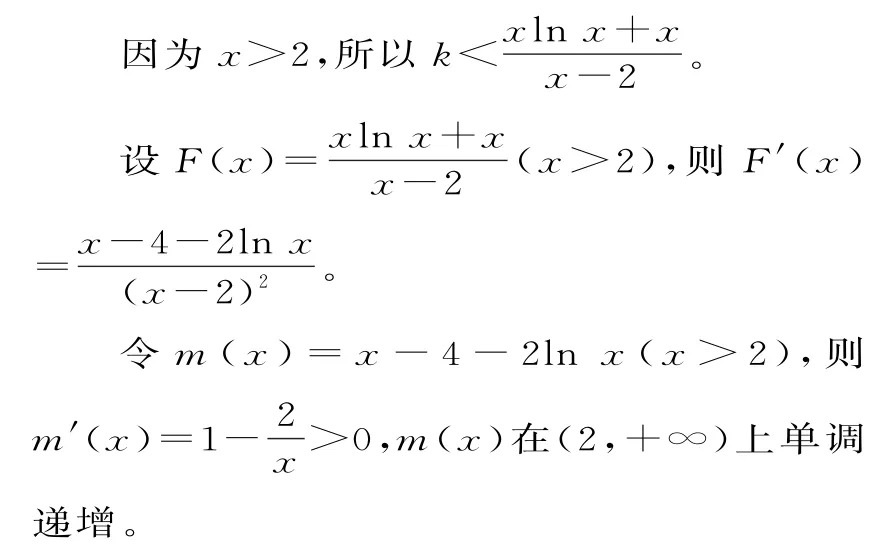
m(8)=4-2ln 8＜4-2ln e2=4-4=0,m(10)=6-2ln 10＞6-2ln e3=6-6=0。

所以函數(shù)m(x)在(8,10)上有唯一的零點x0,即x0-4-2lnx0=0。當(dāng)2＜x＜x0時,m(x)＜0,即F'(x)＜0;當(dāng)x0＜x時,F'(x)＞0。

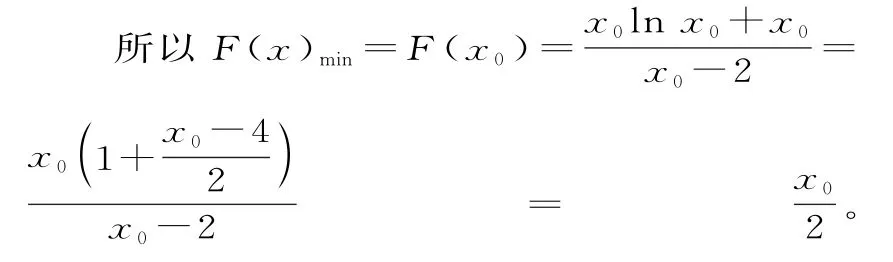
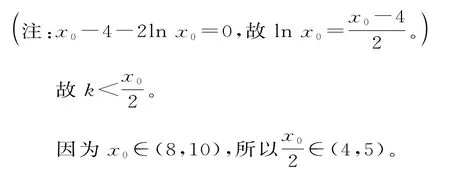
k的最大值為4。

注意：m(x0)=0,即x0-4-2lnx0=0的應(yīng)用。

例3證明：x＞0,x-xlnx≤e-x+x2。

證明：要證x-xlnx≤e-x+x2,只需證e-x+x2-x+xlnx≥0。

設(shè)h(x)=e-x+x2-x+xlnx,x＞0,則h'(x)=-e-x+2x+lnx。

令g(x)=h'(x),則g'(x)=e-x+2+,所以函數(shù)h'(x)=-e-x+2x+lnx單調(diào)增。

所以當(dāng)x∈(0,x0)時,h'(x)＜0;當(dāng)x∈(x0,+∞)時,h'(x)＞0。函數(shù)h(x)在(0,x0)上單調(diào)遞減,在(x0,+∞)上單調(diào)遞增,故

因為1+x0＞0,所以只要x0+lnx0≥0即可。

當(dāng)x0+lnx0＜0時,lnx0＜-x0?x0＜,所以x0+lnx0＜0 與矛盾,故x0+lnx0≥0,得證。

注意：h'(x0)=0,即=0的應(yīng)用。本題中還應(yīng)用了反證法來證明不等式x0+lnx0≥0。

例4已知函數(shù)f(x)=2ex-(x-a)2+3,a∈R,若x≥0,f(x)≥0 恒成立,求a的取值范圍。

解析：f'(x)=2(ex-x+a)。令h(x)=2(ex-x+a)(x≥0),則h'(x)=2(ex-1)≥0。

故h(x)在[0,+∞)上單調(diào)遞增,且h(0)=2(a+1)。

①當(dāng)a≥-1 時,f'(x)=h(x)≥0 在[0,+∞)上恒成立,即函數(shù)f(x)在[0,+∞)上單調(diào)遞增。

②當(dāng)a＜-1 時,則存在x0＞0,使h(x0)=0。當(dāng)x∈[0,x0)時,h(x)＜0 即f'(x)＜0,則f(x)單調(diào)遞減;當(dāng)x∈(x0,+∞)時,h(x)＞0,則f'(x)＞0,f(x)單調(diào)遞增。

故M(x)在(0,ln 3]上單調(diào)遞減,M(x)≥M(ln 3)=ln 3-3,M(x)＜M(0)=-1,ln 3-3≤a＜-1。

注意：h(x0)=0,即的應(yīng)用。另外,本題中先求出零點x0的取值范圍,再建立關(guān)于a的函數(shù),從而得到a的取值范圍。

利用導(dǎo)數(shù)解決含參不等式恒成立問題的兩種常用方法：(1)分離參數(shù)法,將原不等式分離參數(shù),轉(zhuǎn)化為求不含參數(shù)的函數(shù)的最值問題,利用導(dǎo)數(shù)求得所求范圍,一般地f(x)≥a恒成立,只需f(x)min≥a,而f(x)≤a恒成立,只需f(x)max≤a;(2)函數(shù)思想法,將不等式轉(zhuǎn)化為含待求參數(shù)的函數(shù)的最值同題,利用導(dǎo)數(shù)求該函數(shù)的極值(最值),然后構(gòu)建不等式求解。

有些題目無法用分離參數(shù)求得,或者比較復(fù)雜,這時只能用分類討論的方法求解。幾種方法要靈活運用。

例5已知函數(shù),且曲線y=f(x)在點(1,f(1))處的切線方程為y=x-1。

(1)求實數(shù)m,n的值及函數(shù)f(x)的最大值;

解析：(1)函數(shù)f(x)的定義域為(0,+∞),f'(x)=。因為f(x)的圖像在點(1,f(1))處的切線方程為y=x-1,所以

令f'(x)=0,得x=e。

當(dāng)0＜x＜e時f'(x)＞0,f(x)單調(diào)遞增;當(dāng)x＞e時f'(x)＜0,f(x)單調(diào)遞減。

所以當(dāng)x=e時f(x)取得最大值,最大值為

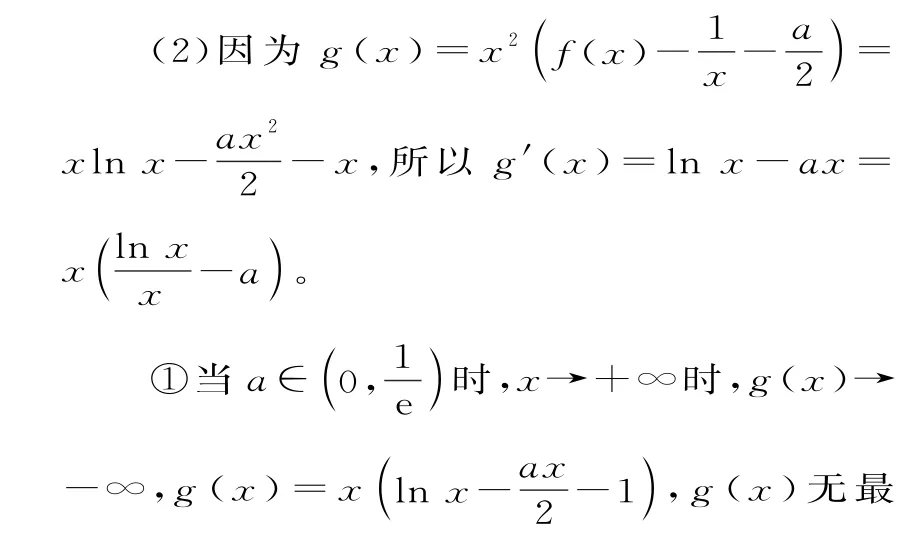
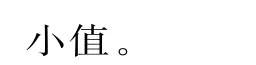
②當(dāng)a=0時,g'(x)=lnx,由g'(x)＞0,得x＞1;由g'(x)＜0,得0＜x＜1。

所以g(x)在(0,1)上單調(diào)遞減,在(1,+∞)上單調(diào)遞增,g(x)的最小值b=g(1)=-1。

當(dāng)x∈(0,t)時,g'(x)＜0,當(dāng)x∈(t,+∞)時g'(x)＞0,所以g(x)在(0,t)上單調(diào)遞減,在(t,+∞)上單調(diào)遞增,g(x)的最小值注意利用lnt=at代入,可換掉字母a得到一個關(guān)于t的函數(shù),令在上單調(diào)遞減。

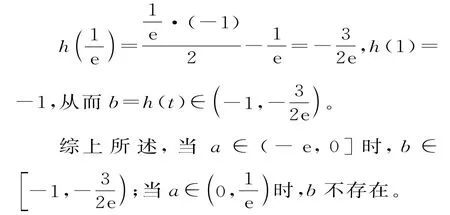
函數(shù)、導(dǎo)數(shù)、不等式的綜合問題是近幾年高考的熱點問題,這類問題往往以“參數(shù)處理”為主要特征,“導(dǎo)數(shù)運用”為主要手段,“函數(shù)的單調(diào)性、極值、最值”為結(jié)合點,常涉及導(dǎo)數(shù)、不等式、方程等多方面的知識,需要綜合運用化歸與轉(zhuǎn)化、分類討論、數(shù)形結(jié)合等數(shù)學(xué)思想方法求解。