一種基于北斗導航系統的多天線定向測姿方法研究
簡海波,汪 捷
(海軍工程大學電子工程學院,湖北 武漢 430033)
2018年12月27日,中國自主研制的北斗導航系統正式開放全球定位服務,這將對衛星導航技術的研究和應用帶來深遠影響[1]。衛星導航具有全天候、全地形等優勢,在國民經濟和社會發展的各個方面應用廣泛。其中,早在21世紀初期利用衛星導航技術實現物體定向[2]已經開始了研究和應用,在定向的基礎上實現姿態測量[3]儼然是現在研究的熱門。傳統的姿態測量手段多以慣性器件為主。慣性器件測量姿態具有穩定度高,測量快速等優點,但是慣性器件具有誤差積累[4],在較長時間后,無法保證高精度姿態信息的輸出。在追求效率的時代,無論是軍事應用還是民用都在想辦法提高或改變姿態的測量方式。因此,本文提出一種基于北斗的多天線姿態解算方法。
1 北斗定向測姿原理
通過任意布設的三天線只要滿足天線不共線就可以得到2個不相關的基線向量,通過向量的投影關系及向量和平臺坐標的轉換關系即可得到平臺的三維姿態信息[5-6]。
偏航角為
(1)
俯仰角為
(2)
滾動角為
(3)
式中,xli、yli、zli均為坐標轉換之后的基線向量坐標。三天線測姿方法可擴充至四天線以上,當采用四天線以上的姿態測量時,可以對基線向量進行網平差運算[7]。
2 單頻單歷元模糊度解算方法
各個基線向量解算的過程中,關鍵是模糊度的快速精確固定[8-9]。由于平臺的天線陣列基線長度已知,可以改進載波相位差分定位中的模糊度算法,在LAMBDA算法[10]中加入限定方程可使得單頻單歷元的LAMBDA解算系數矩陣不再秩虧[11],這種方法也稱CLAMBDA算法或阻尼LAMBDA算法[12]。
根據LAMBDA算法,模糊度參數a的搜索空間可以充分利用基線長信息限制基線分量的二次型最小
ΩF(χ2)={a∈Z|F(a)≤χ2}
(4)
其中
(5)
(6)
ΩF(χ2)?ΩE(χ2)
(7)
ΩF(χ2)={a∈Zn|F(a)≤χ2}
(8)
(9)
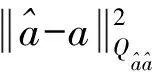
根據CLAMBDA方法的原理,設計CLAMBDA方法的具體實現流程如下:
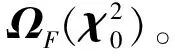
(10)
(11)
(12)
式(12)可以保證在進行模糊度搜索時,至少有一個整數模糊度候選點,并且滿足對應的F(a)不大于χ2(0)。
(2) 根據SE-VB算法[13]求取第一個整周模糊度候選解a1。首先要求解基線分量b,式(6)滿足如下函數模型
(13)
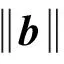
(14)
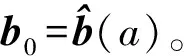
(15)
式中,Δb=[ΔxΔyΔz]T。對式(15)進行經典的最小二乘平差,可求出b1。再將b1作為初值進行最小二乘解算,重復以上迭代步驟直到bn和bn-1的差值小于設定的閾值。此時b=bn。再根據式(5)、式(6)即可求取F(a1)。
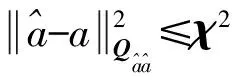
由于加入了基線長約束條件,模糊度最優解必須同時滿足模糊度和基線向量的二次型最小,此時模糊度搜索空間[14]已經不為橢球。相比無基線長約束,基線長條件縮小了模糊度的搜索空間,提高了模糊度的搜索效率。由于模糊度最優解同時要滿足基線向量二次型最小,因此該方法還可以在一定程度上提高基線向量精度[15]。上述算法在模糊度沒有周跳[16]的前提下可以有效地解算單頻單歷元基線向量。
3 試驗案例
根據一組天線觀測數據,利用自編解算程序模擬姿態測量。分別對三天線姿態測量和四天線平差測量的結果進行比較。總共接收4個天線的數據,其中主天線與其余天線之間的距離分別為9.910、15.219、18.103 m。利用3個天線進行直接姿態測量得到的姿態信息和四天線平差結果如圖1所示。
從圖1和圖2中看,平差計算平滑了姿態數據曲線,使姿態測量誤差更小,通過與慣性測量儀器輸出的姿態信息進行比對,直接測量誤差約為0.12°,采用四天線平差處理的測量誤差約為0.107°。
為了進一步驗證本文提出的姿態測量算法在動態基線解算中的可行性,進行了動態三天線姿態解算試驗。三天線均架設于觀測狀況良好的屋頂試驗平臺,試驗過程中,先保持三天線靜態測量數分鐘,而后模擬平臺運動,將其中一個接收機天線上下運動一段時間,然后回到初始位置靜態測量數分鐘。得到的三天線觀測數據進行姿態解算結果如圖3所示。
從圖3可以看出,姿態的變化可以分為3段,0~200歷元屬于靜態,在200~300歷元姿態來回變化,在300~450歷元姿態重新回復穩定。驗證了此方法可用于實時姿態測量。
4 結 語
本文在LABMDA算法的基礎上研究并提出了C-LABMDA算法的實現步驟,為驗證算法的可靠性,進行了仿真與實測試驗。從試驗結果中可以看出,本文所提出的平臺姿態解算方法在靜態和動態條件下均可正確解算,此方法可以廣泛應用于車輛、艦船等運動平臺的姿態信息實時獲取。

