雙層網絡上的社會傳播

李小林，許潤杰，婁 潔，許新建

(上海大學數學系，上海 200444)

0 引言

作為社會群體，人與人之間總是不斷地交流來傳播信息和觀點，這種人際溝通、影響、傳遞的過程稱為社會傳播。如何模擬這種人際傳播是社會網絡研究中的一個基本問題[1]。一般地，傳播可以分為簡單傳播和復雜傳播[2]。所謂簡單傳播是指任意一對不同狀態個體之間傳染的發生僅僅依賴一個獨立參數——傳染率，而與周圍鄰居的狀態無關，從而服從泊松過程。這一假設在經典流行病研究中被廣泛采用[3]，因此生物傳播屬于典型的簡單傳播。而復雜傳播往往考慮局部依賴性和時間記憶性，例如一個觀點如果來自于多個不同渠道，那么它更容易會被接受，因此社會傳播屬于典型的復雜傳播。

關于社會傳播的研究最早可以追溯到1973年Schelling提出的閾值模型[4]。該模型假設系統中的個體有兩個狀態：0和1。對于一個狀態為0的個體，當其狀態為1的鄰居數目或比例超過一個臨界值時，個體的狀態也從0轉變為1。以社會罷工為例，一個人是否參加罷工的閾值可以定義為其周圍有多少或多大比例的人已經參加了罷工，如果這個人是激進的，那么他的理性閾值可能較低，如果這個人是保守的，那么他的理性閾值相對較高。

雖然閾值模型的研究在社會學[5]和經濟學[6]中早已展開，但是直到2002年才引入接觸網絡[7]。Watts利用母函數方法計算了傳播條件和感染規模，他發現個體的閾值差異性和結構異質性對傳播起著完全相反的作用：一方面，個體的內在閾值差異性越強，觀點越容易擴散，或者說系統越容易發生全局崩潰(global cascade)；另一方面，個體的外在結構異質性越強(如度的異質性)，觀點越不容易擴散(no cascade)，即系統的魯棒性越好。這一有趣的結論引起了廣大研究者的興趣，紛紛投入這一領域。一方面，研究者開始考慮更多的網絡結構特征對傳播的影響，如度相關[8]、集聚系數[9]、時效[10]、有向[11]等。另一方面，更多的傳播機制被提出，如媒體影響力[12]、多階段擴散[13]、個體記憶性[14]、信念堅定[15]等。在這些研究中，傳播往往都是限制在單個網絡上。

上述研究相對簡單，無論是線下網絡還是線上網絡都采用Erd?s-Rényi(ER)隨機圖[22]，沒有考慮結構異質性，而實證研究早已表明絕大數的在線網絡都是非均勻的[23]。鑒于這一點，本文采用scale-free(SF)網絡[24]來模擬線上網絡，并構造ER-SF雙層網絡，研究線下均勻網絡與線上非均勻網絡的耦合關系對社會傳播的影響。

1 模型

為了研究方便，我們考慮節點一一對應的的雙層社會網絡。如圖1所示，網絡中的任意一點i(i=1,2,…,n)既有線下鄰居也有線上鄰居，其個數分別可以用線下度ki,α和線上度ki,β來表示。即使點i的線下度與線上度相等，其連接的鄰居也未必相同。已有研究假設網絡的度分布是均勻的[16-17]，即對同一層網絡來說，所有節點的度值都差不多，典型模型是ER隨機圖[22]，其度分布滿足泊松分布p(k)～zke-k/k!，其中p(k)表示單層網絡中任意一點度為k的概率，z是該層網絡中所有節點的平均度。使用ER模型可以較好地模擬線下網絡，但是線上網絡中個體的差異非常大(如度的異質性)，使用非均勻網絡更恰當，典型模型是Catanzaro等人提出的SF配置網絡[24]，其度分布滿足冪律分布p(k)～k-γ，其中γ是控制度分布指數的參數。

圖1 3種耦合網絡示意圖

進一步，考慮線下ER網絡和線上SF網絡基于度的3種耦合情況[25]：完全不相關(no correlation，簡稱nc)，完全正相關(maximum positive，簡稱mp)，完全負相關(maximum negative，簡稱mn)。完全不相關是指兩層網絡中節點度之間不存在相關性，此時整個網絡節點度的聯合概率分布為

(1)

完全正相關是指節點在線下網絡中的度越大(或越小)則它在線上網絡中的度也越大(或越小)，此時節點度的聯合概率分布為

(2)

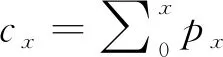
(3)

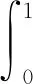
(4)

其中，μα和μβ分別表示節點在線下網絡和線上網絡中的理性閾值，mα和mβ分別表示節點線下鄰居和線上鄰居中狀態為1的個數。

給定一個初始種子，傳播能夠進行下去的必要條件是網絡中存在脆弱點。所謂脆弱點是指節點在線下網絡或線上網絡中只要有一個鄰居處于接受狀態它就會被激活，根據式(4)，相應的概率可以寫為

(5)

(6)

由此，線下網絡和線上網絡中脆弱點度分布的母函數可定義為

(7)

(8)

進一步，在線下網絡或線上網絡中隨機選擇一條邊，其連到脆弱點的概率分別為

(9)

(10)

其中zα和zβ分別表示線下網絡和線上網絡的平均度。傳播要形成規模，則要求網絡中存在脆弱分支。在網絡中隨機選擇一點，其與脆弱分支相連的概率可定義為

(11)

其中，H1,α(x)和H1,β(x)分別表示線下網絡和線上網絡中隨機選擇一條邊，其與脆弱分支相連的概率，

H1,α(x)=[1-G1,α(1)]+xG1,α(H1,α(x))
H1,β(x)=[1-G1,β(1)]+xG1,β(H1,β(x))

(12)

根據滲流理論，系統發生全局崩潰對應著脆弱巨分支的出現，即方程(12)的雅可比矩陣的譜半徑大于1[16]，

(13)

其中，Jij(i,j=1,2)為方程(12)的雅可比矩陣元，即

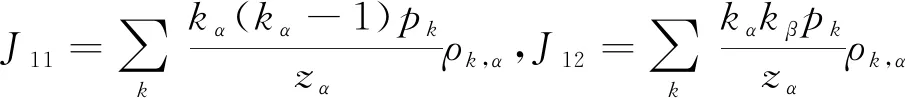
(14)

由H0(x)的定義可知，H0(1)表示網絡中隨機選擇一點到達脆弱小分支的概率(包括到達脆弱規模為0的情形)，因此脆弱巨分支的大小為

Sv=1-H0(1)

(15)

2 結果

對于一一對應的雙層網絡來說，線下ER網絡和線上SF網絡的規模必然相等，即Nα=Nβ=N。考慮可比性，令線下網絡和線上網絡的平均度相等，即zα=zβ=z。為了計算方便，規定每層網絡中的個體閾值都相同，即μi,α=μi,β=μ。初始時刻隨機選擇一個節點作為傳染源，令其狀態為1，其余節點狀態為0。分別在完全不相關，完全正相關及完全負相關三種耦合下的ER-SF雙層網絡(N=10 000)上各進行了100次蒙特卡羅模擬，計算了脆弱巨分支和崩潰條件，并同式(15)和(13)進行了對比。

當線下網絡和線上網絡的耦合完全不相關時，網絡中點i的線下度ki,α和線上度ki,β無關(見式(1))。在給定閾值條件下，i是否被激活取決于ki,α和ki,β的大小，而對整個耦合網絡來說，脆弱巨分支Sv是否出現則與平均度z密切相關。如圖2a所示，圓點是網絡上100次模擬的結果，實線是式(15)的理論預測，在μ=0.24條件下，當z很小時(低連通區域)，網絡非常稀疏，傳播無法進行。隨著z的增加，Sv從0變到大于0，網絡開始發生崩潰，對應的平均度臨界值zl稱為崩潰下界。進一步增加z，脆弱點之間連通性不斷增強，導致Sv越來越大。然而，當z很大時(高連通區域)，式(5)和(6)成立非常困難，即脆弱點不斷減少，網絡不再發生崩潰，對應的平均度臨界值zh稱為崩潰上界。作為對比，ER-ER雙層網絡的結果也一并給出。盡管模擬結果存在一定的漲落現象，但是和理論結果(式(15))符合較好。在此基礎上，圖2b給出了(μ,z)雙參相圖，方格是網絡上100次模擬的結果，實線是式(13)的理論預測。隨著個體閾值μ和網絡連通性z的變化，系統存在一個崩潰窗口，與式(13)的預測一致，即系統在窗口內部發生全局崩潰而在窗口外部不發生崩潰。在崩潰下界(zl≤1)，網絡中大部分的節點度為0或1，線上SF網絡限于度分布的異質性，其孤立點的數目比線下ER網絡更多，所以ER-SF雙層網絡的魯棒性優于ER-ER雙層網絡。在崩潰上界(zh>2)，線下ER網絡的節點度值整體都會增大，脆弱點很難出現，而線上SF網絡的異質性卻進一步增強，一方面大量的低度節點依舊存在，可以成為脆弱點，另一方面，大度節點的數目有所增加，一旦成為種子將會促進傳播，所以ER-SF雙層網絡的魯棒性劣于ER-ER雙層網絡，這種差別隨著z的增加不斷增大。

圖2 完全不相關耦合下的脆弱巨分支和崩潰窗口

當線下網絡和線上網絡的耦合完全正相關時，網絡中點i的線下度ki,α越大，其線上度ki,β也越大，整個網絡的聯合度分布服從式(2)，仍然可以代入式(13)和(15)求出理論結果。圖3給出了脆弱巨分支和崩潰窗口的計算結果，圓點和方格是網絡上100次模擬的結果，實線是式(15)和(13)的理論預測。當網絡的連通性很弱時，盡管每層網絡都非常稀疏，但仍然存在少數度大于等于1的節點，完全正相關保證了一旦某節點在下層的度大于等于1，其在上層的度也必然大于等于1。如果這類節點在某一層的某個鄰居是初始種子，那么它們很有可能成為脆弱點而被激活(見式(5)和(6))，不但會在該層繼續激活其它鄰居，而且會通過另一層的網絡進行傳播。最終這些非孤立點可能會導致一個小規模的崩潰。如圖3a所示，即使在z=0.1時，無論是ER-ER網絡還是ER-SF網絡在正相關下都有大約9%的節點會被感染。而線上SF網絡的非均勻性使得ER-SF網絡略易于傳播。當網絡的連通性很強時，無論是哪一層網絡中的節點都很難成為脆弱點。即使線上SF網絡有一些小度節點成為脆弱點，一方面其線上較少的鄰居數目使得傳播困難，另一方面其在線下ER網絡的度相對較大不易成為脆弱點，從而阻礙進一步傳播，因此ER-SF網絡比ER-ER網絡魯棒性更強，如圖3b所示。

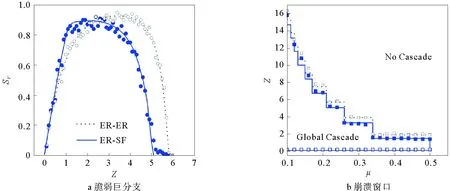
圖3 完全正相關耦合下的脆弱巨分支和崩潰窗口

當線下網絡和線上網絡的耦合完全負相關時，網絡中點i的線下度ki,α越大，其線上度ki,β卻越小，整個網絡的聯合度分布服從式(3)，仍然可以利用式(13)和(15)算出理論結果。在低連通區域，盡管節點在某層網絡的度可能為0，但是負相關耦合保證了其在另一層網絡的度不為0，所以網絡中線下度和線上度都不為零的節點相對較少，這將大大削弱跨層傳播，傳播主要依賴單層網絡，脆弱點形成巨分支比較困難，不過一旦網絡中出現脆弱巨分支，規模將會較大，如圖4a所示。而在高連通區域，完全負相關耦合使得ER-SF網絡比ER-ER網絡的魯棒性略差，如圖4b所示。相對于ER-ER雙層網絡中脆弱點大比例減少，ER-SF網絡則不同，負相關使得下層ER網絡中小度節點對應上層SF網絡中的hub節點，一旦這些小度節點在ER層成為脆弱點，它們在SF層的hub效應將使傳播仍有可能進行下去，即跨層傳播在一定程度上削弱了系統的魯棒性。

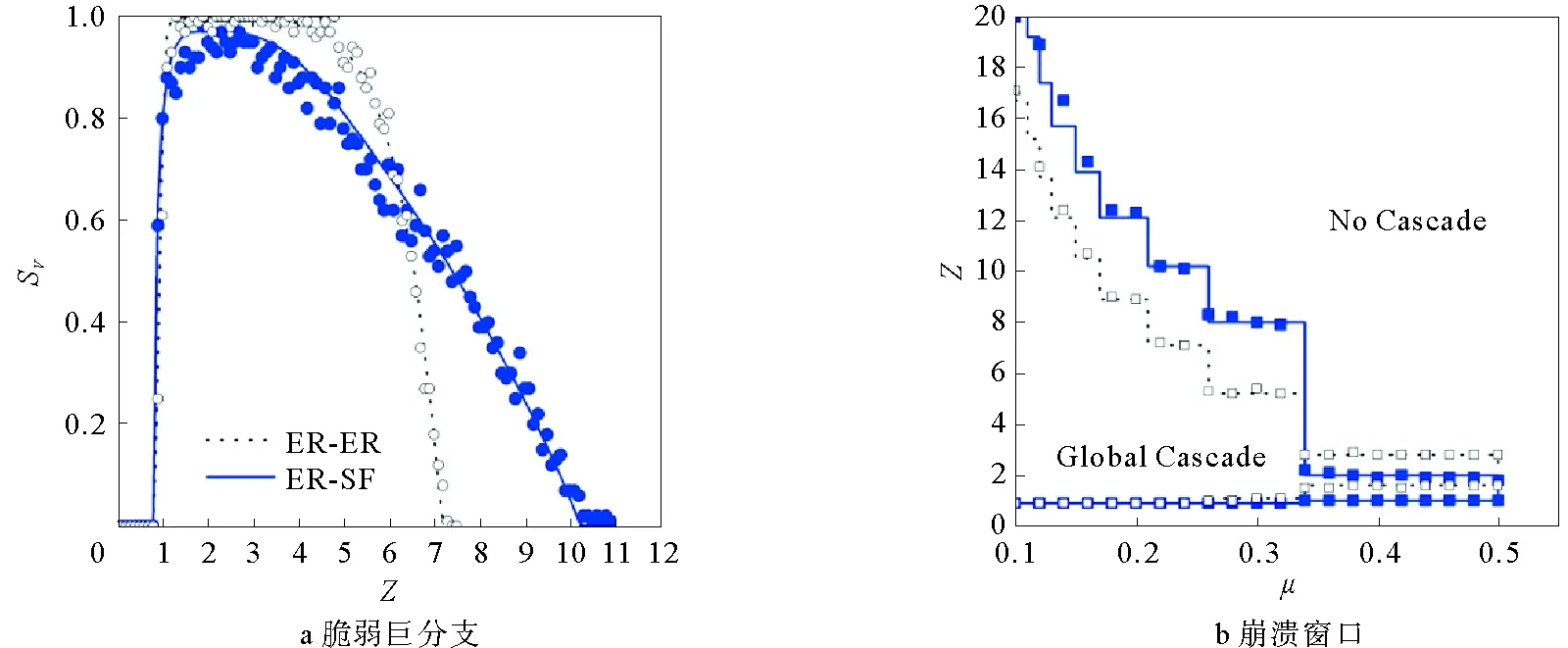
圖4 完全負相關耦合下的脆弱巨分支和崩潰窗口

3 結論

自“計算社會學”[26]這一概念于2009年在科學雜志上提出以來，無論是傳統的社會學家，還是數學家和計算機學家都紛紛進入這一新興領域。如何提供新的模型和方法來解釋社會現象和數據規律是一個充滿挑戰性的課題，而復雜網絡理論是當前國際上公認的研究計算社會學的有效工具之一。

本文研究了線下ER網絡和線上SF網絡協同傳播這一問題，比過去純粹考慮線下線上都是ER網絡更貼近實際。針對ER-SF雙層網絡上的閾值模型，利用母函數方法得到了系統發生全局崩潰的條件和相應脆弱巨分支的大小，并分別應用到完全不相關，完全正相關及完全負相關三種耦合情形中。與完全不相關耦合相比，完全正相關耦合在低連通區域會削弱系統的魯棒性而在高連通區域會增強系統的魯棒性，完全負相關耦合則會導致相反的結果。進一步，通過比較ER-SF雙層網絡和ER-ER雙層網絡在不同耦合下的崩潰結果，發現在完全正相關耦合下，ER-SF雙層網絡比ER-ER雙層網絡在低連通區域魯棒性更差而在高連通區域則相反；在完全負相關耦合下，ER-SF雙層網絡比ER-ER雙層網絡在低連通區域魯棒性更好而在高連通區域則相反。

上述結果是在“或”激活機制和全同閾值兩個條件下得到的。一個自然的延伸是把上述理論推廣到更加復雜的情形，如“與”激活機制和分布閾值的情形，但相應的計算量也大大增加。