國際股市隱含波動率溢出效應分析

陳志英，肖忠意，李永奎

(西南政法大學 a.經濟學院；b.民營經濟研究中心，重慶 401120)

0 引言

隨著經濟全球化、金融市場一體化的推進，全球金融市場的聯系日趨緊密，金融風險之間的交互反饋機制和傳導鏈條日趨復雜。近年來發生的金融危機(次貸危機、歐債危機)的教訓告訴我們，全球金融市場聯動性的加強，常常使得爆發于某一市場的金融波動迅速蔓延至其他金融市場。因此，準確度量金融市場波動的傳遞結構并識別其產生過程，對于防范系統性金融風險、建立有效金融風險監管，具有極強的理論和現實意義。

鑒于理論和實踐上的重要性，國內外學者針對國際股票市場間的波動溢出效應開展了卓有成效的研究。早期的大量研究探索了跨市場波動溢出的產生機理，大致分為經濟基礎假說和市場傳染假說[1]。經濟基礎假說認為，經濟基本面的相互關聯[2]，比如貿易聯系程度[3]、金融市場發展情況[4]、貨幣政策同步性[5]以及資本跨國跨境流動導致了國際間股市的聯動[6]。但King，Wadhwani[7]提出市場傳染假說，即在經濟基本面沒有發生變化的情況下，僅僅一個市場的價格波動本身就能對另一個市場產生影響，尤其是在市場波動幅度較大時，投資者的情緒和行為在跨市場聯動中起主要作用[8]。張兵等[9]認為經濟基礎假說和市場傳染假說并不是割裂的，二者是對立統一。近年來，另外一些學者指出跨國機構投資者在全球資產配置中的調倉或拋售行為將通過共同持有資產導致資產價格聯動，造成跨市場的風險傳染[10-13]。

在研究方法方面，針對波動溢出效應的衡量方法也在不斷地演化、創新。其中，最常用的一類方法是VAR模型加上GARCH族及其衍生模型。學者們應用此類方法對國際股票市場、各類金融資產、各金融機構之間的波動溢出效應進行了廣泛的研究。Cheung，Ng[14]、Hong[15]提出的樣本交叉相關函數(CCF)也是一種較為常見的波動溢出檢驗方法[16]。但是GARCH族模型和CCF方法主要適用于從全樣本視角檢驗市場間的波動溢出效應，大多只能檢驗兩兩市場間的溢出效應，無法刻畫所有市場的整體波動溢出效應、各市場的溢出貢獻度以及市場間波動溢出的時變特征[17]。

近年來，Diebold，Yilmaz[18-19]提出的溢出指數方法(Spillover Index)，受到學術界的廣泛關注。該方法基于VAR模型的廣義方差分解進行構建，從而消除了變量順序對正交分解結果的影響；而且采用滾動窗口的VAR模型可以構建時變的總體溢出指數和分市場的溢出、溢入指數，從而可以探討不同市場間的互相溢出效應。與以往方法相比，該方法不僅給出了波動溢出的方向，而且能夠測度波動溢出的強度、規模及時變性特征。近年來，大量研究采用溢出指數方法對金融市場或金融資產之間的波動或信息溢出效應進行研究。Yang，Zhou[20]、Greenwood等[21]采用溢出指數方法研究了全球主權國家及主要金融機構的信用風險溢出效應。梁琪等[22]通過測度中國股市信息溢出的方向、水平和動態趨勢以衡量中國股市的國際化水平。周開國等基于類似的分析框架探討了香港股市對亞太地區股市影響力的變化趨勢[23]。其他研究如劉超等[24]、李政[25]、尹力博和吳優[26]分別研究了中國金融市場的波動溢出、人民幣匯率中間價的市場基準地位以及離岸人民幣的區域影響力。特別地，Yang，Zhou[27]利用溢出指數方法提取VIX對全球主要金融市場及商品市場的波動溢出強度，考察美國量化寬松政策對這種波動溢出強度的影響。

基于以上分析，本文采用最新的溢出指數和復雜網絡方法[18-20]，基于全球11個代表性國家及地區股市的隱含波動率指數，對各金融市場的波動率溢出效應及其影響因素進行全面研究。與本文研究最為接近的是Yang，Zhou[27]，但二者的研究目的不同。Yang，Zhou[27]主要考察美國量化寬松政策對國際主要金融市場間波動溢出的影響，而本文的重點是度量國際主要金融市場波動溢出效應的方向、水平和動態趨勢，并分析影響波動溢出的主要因素。與以往研究相比，本文具有如下特點：

首先，本文采用隱含波動率指數對波動溢出效應進行分析。以往對股票市場波動溢出的研究主要采用歷史收益率數據使用某些計量方法估計而來的波動率進行分析。而隱含波動率指數是從市場交易的一系列期權價格中反推出來的波動率，與依據歷史數據估計的波動率測度相比，隱含波動率指數具有如下顯著的優點：第一，由于期權的價格和交易中隱含著現貨未來預期的信息，從而從期權價格中反推出來的隱含波動率指數反映了投資者對期權標的資產未來波動率的預期，因此與其他波動率測度相比，隱含波動率指數更具前瞻性和準確性，所具有信息含量更為豐富[28-29]。第二，目前全球主流的隱含波動率指數均采用無模型方法構建，從而避免了內生的模型風險。另外，本文選擇了全球11個主要的隱含波動率指數(涵蓋了發達市場和新興市場)進行分析，研究的樣本具有代表性。

其次，雖然一些研究也采用隱含波動率指數探討波動溢出效應，如ij?[30]、Jiang等[31]、Peng，Ng[32]、Kenourgios[33]、Badshah[34]等人的研究。但這些研究只是驗證了波動溢出效應的存在性，以及兩個市場間波動溢出的領先滯后關系，并沒有刻畫波動溢出的時變特征以及各市場之間的聯接關系。本文采用最新的溢出指數和復雜網絡方法進行分析，不僅能夠刻畫各市場之間波動溢出的關聯關系，測度波動溢出的方向和強度，而且基于滾動方法構建的溢出指數能夠捕捉波動溢出的時變特征，這對于金融監管更具有參考價值。

最后，本文首次深入地分析了波動溢出背后的宏觀和微觀影響因素。從經濟基礎和市場傳染兩個視角，檢驗了貿易關聯、資本流動、市場波動等因素對波動溢出的影響。這些研究有助于理解波動溢出的形成機理，為全球的金融監管提供有益參考。

1 樣本數據與研究方法

1.1 樣本數據說明

隱含波動率指數是從市場交易的一系列期權價格中反推出來的波動率。由于其具有預示市場動蕩的作用，亦被稱為“恐慌指數”。1993年美國芝加哥商品交易所(CBOE)編制了全球第一只波動率指數(CBOE Volatility Index，VIX)。該指數自發布以來，已成為全世界衡量投資者情緒和市場波動的最重要指數。此后，全球各主要金融市場都依照類似的方法發布了本國或本地區的VIX指數。

本文選取了11個代表性的國家和地區的主要股票市場指數的隱含波動率指數作為研究對象，樣本指數涵蓋了發達市場和新興市場，均采用無模型方法構建，具體指數如下：VIX(美國S&P 500波動率指數)、VDAX-NEW(德國DAX 30波動率指數)、VCAC(法國CAC 40波動率指數)、VFTSE(英國FSTE 100波動率指數)、VIXC(加拿大S&P/TSX 60波動率指數)、AXVI(澳大利亞S&P ASX 200波動率指數)、VXJ(日本Nikkei 225波動率指數)、VHSI(中國香港恒指波動率指數)、VKOSPI(韓國KOSPI 200波動率指數)、India VIX(印度Nifty 50波動率指數)、TWVIX(中國臺灣臺指期權波動率指數)。由于VIXC的數據起始日為2009年10月1日，故本文樣本期限為2009年10月1號至2018年7月31號，數據樣本為日度數據，所有數據來自Bloomberg數據庫和各交易所網站。

由于波動率具有持續性、高度自相關的特征，因此我們對各隱含波動率指數進行一階差分[35]。由于隱含波動率指數近似于方差互換的價格，因此其的一階差分可以理解為方差互換的價格變化。考慮到因時差造成的交易非同步，本文采用隱含波動率指數一階差分的兩日滾動平均值進行研究[36]。表1列出了相應的描述性統計結果。從表中可以看出，在樣本期內除VIX的兩日滾動平均值為正，其它的波動率指數均值都為負。所有的隱含波動率指數都是右偏的，且具有尖峰厚尾特征。J-B統計量表明樣本中所有市場的隱含波動率分布都具有明顯的非正態分布。AR(1)檢驗意味著所有的隱含波動率指數都是序列正相關的。ADF檢驗表明所有的隱含波動率指數都是平穩的。

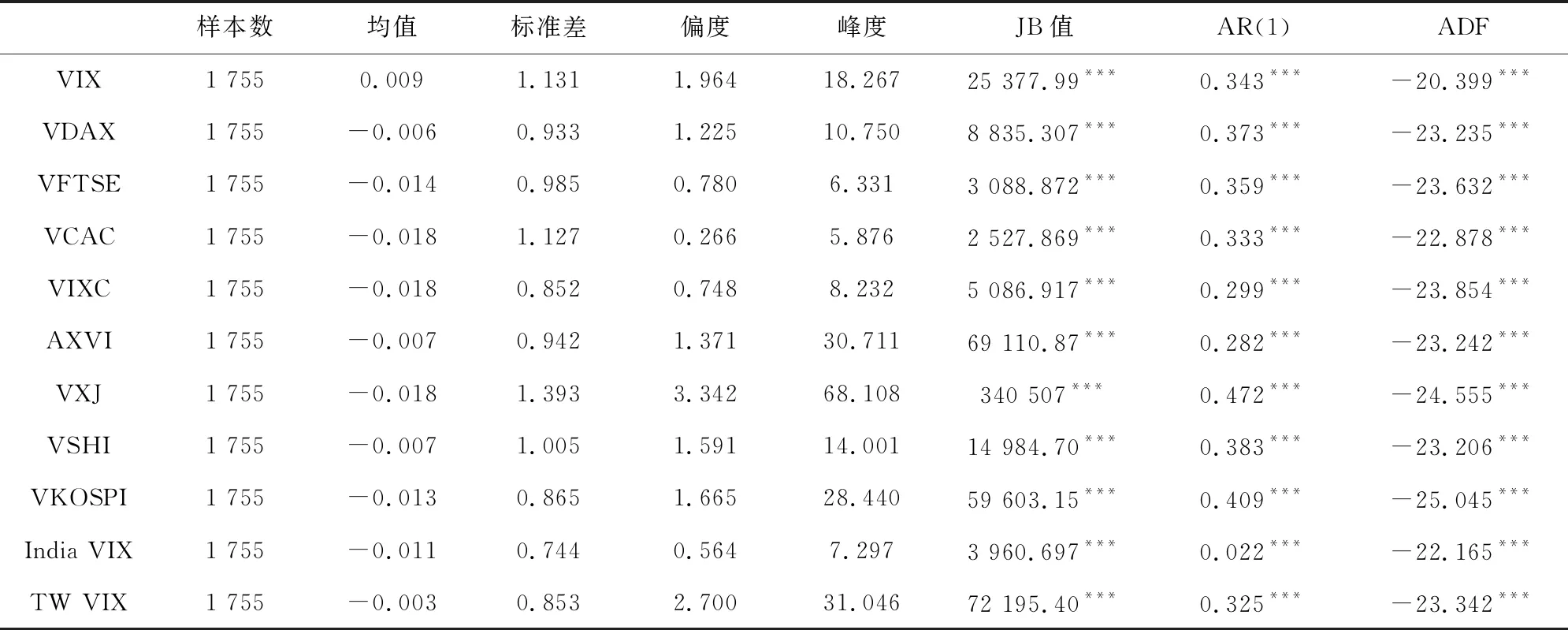
表1 樣本期內隱含波動率指數的統計特征

注：*、**、***分別表示在10%、5%、1%的顯著性水平下顯著。下同。

1.2 隱含波動率溢出指數構建

Diebold，Yilmaz[18-19]提出了基于廣義方差分解構建的溢出指數方法，該方法避免了Cholesky方差分解對變量順序的依賴性，既能刻畫金融市場間風險溢出的強度，還能給出金融市場間風險溢出的方向，成為近年來研究金融市場風險傳染的主要方法。具體模型如下：

首先建立一個具有平穩協方差的滯后p期的N變量VAR模型：

(1)

其中，xt是N維列向量，這里表示隱含波動率指數的一階差分向量。φi是N×N維的系數矩陣，誤差向量εt獨立同分布且均值為零，協方差矩陣為Σ。由于該VAR模型具有平穩的協方差，因此可以將式(1)轉化為移動平均形式：

(2)

其中Ai是滿足遞歸形式Ai=φ1Ai-1+φ2Ai-2+…+φpAi-p的N×N系數矩陣；A0為N×N維的單位矩陣，且當i<0時，Ai=0。由于式(1)的VAR模型需要估計的系數過多，且變量間存在復雜的交互影響，這導致(1)式的估計系數難于直接解釋。因此，(2)式的移動平均系數Ai才是理解該系統動態變化的關鍵[18-19]。

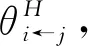
(3)

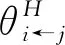
(4)

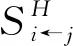
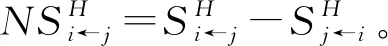
表2 隱含波動率的溢出強度矩陣

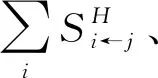
為了衡量N個市場之間波動率的總體溢出水平，可以構造總體波動溢出指數，以考察波動溢出對整個系統變動的平均貢獻比例，計算公式為：

(5)

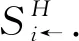
(6)

(7)

2 隱含波動率指數溢出效應檢驗

2.1 溢出效應的靜態檢驗

表1中的ADF檢驗結果表明，在1%顯著性水平下，各隱含波動率序列都是平穩的，可以進一步建立VAR模型。根據AIC和SC準則確定VAR模型的滯后階數為2階，建立VAR模型，對其進行廣義預測誤差方差分解，方差分解期數設定為12期，得到樣本期11個市場隱含波動率指數的溢出表(見表3)。表中的最后1列Sin是某一市場受其他市場的溢入強度，等于每行非對角線元素之和；表中倒數第2行Sto是某一市場對其他市場的溢出，等于每列非對角線元素之和，最后1行Snet是凈溢出效應。

表3顯示，各市場隱含波動率指數受其他市場的影響程度較高且范圍集中，其中VKOSPI受其它市場的影響程度最高。美國VIX是主要的對外溢出市場，其對外溢出值最高(149.4%)，凈溢出值最大(87%)，其次是德國的VDAX、英國的VFTSE和法國的VCAC。這四個市場的凈溢出值為正，其他市場凈溢出值都為負，這說明除了美國、德國、英國、法國市場外，其他市場都是波動率溢出的吸收者。

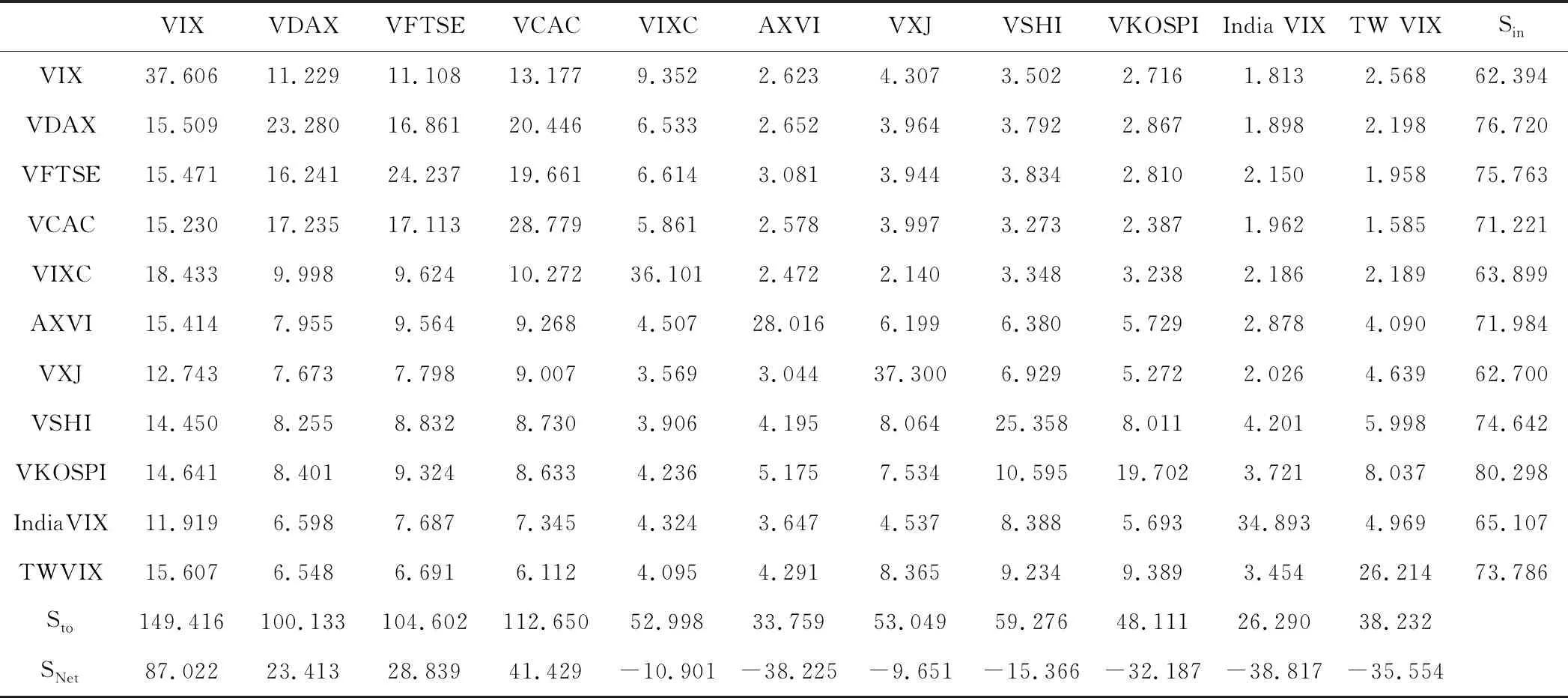
表3 各市場隱含波動率溢出強度矩陣

為了直觀地呈現各市場隱含波動率的溢出強度和方向，我們繪制了隱含波動率溢出網絡，見圖1。從圖中可以看出：VIX是溢出網絡的中心，對其他10個市場都存在明顯的波動溢出。VCAC、VFTSE、VDAX三個市場之間存在非常明顯的相互溢出，但對其他市場的溢出強度較弱。新興市場的對外溢出強度很弱，它們主要是波動溢出的吸收者。圖中的節點表示各市場的隱含波動率指數。點的大小表示一國向外溢出的程度。節點之間的連線表示二者之間的波動溢出效應，線條越粗，則市場之間的波動溢出關系越顯著。這里我們只考慮中位數以上的溢出效應。

2.2 溢出效應的時變特征

為了考察波動溢出的時變特征，本文利用Diebold and Yilmaz[18-19]的滾動窗口VAR方法計算時變的總波動溢出指數和方向性溢出指數。滾動窗口為500天，預測步長為12期。圖2和圖3分別給出了總波動溢出指數圖和方向性溢出指數圖。從圖2中可以看出，一方面，2010—2018年期間，全球主要金融市場的波動率溢出指數維持在50%到85%之間，整體風險聯動性較強。另一方面，總波動溢出指數存在一定的波動性，受危機及股市波動等極端事件影響較大。2011年至2012年受歐債危機的影響，總波動溢出一直在高位波動，此后緩慢下行；2015年年中，中國股市暴跌，總波動溢出指數隨之迅速上升，從56%上升至76%；此后，受英國脫歐事件的影響，總波動溢出指數持續維持在較高水平；2018年2月，美國股市暴跌，總波動溢出指數再次急劇上升，但上升幅度不大。

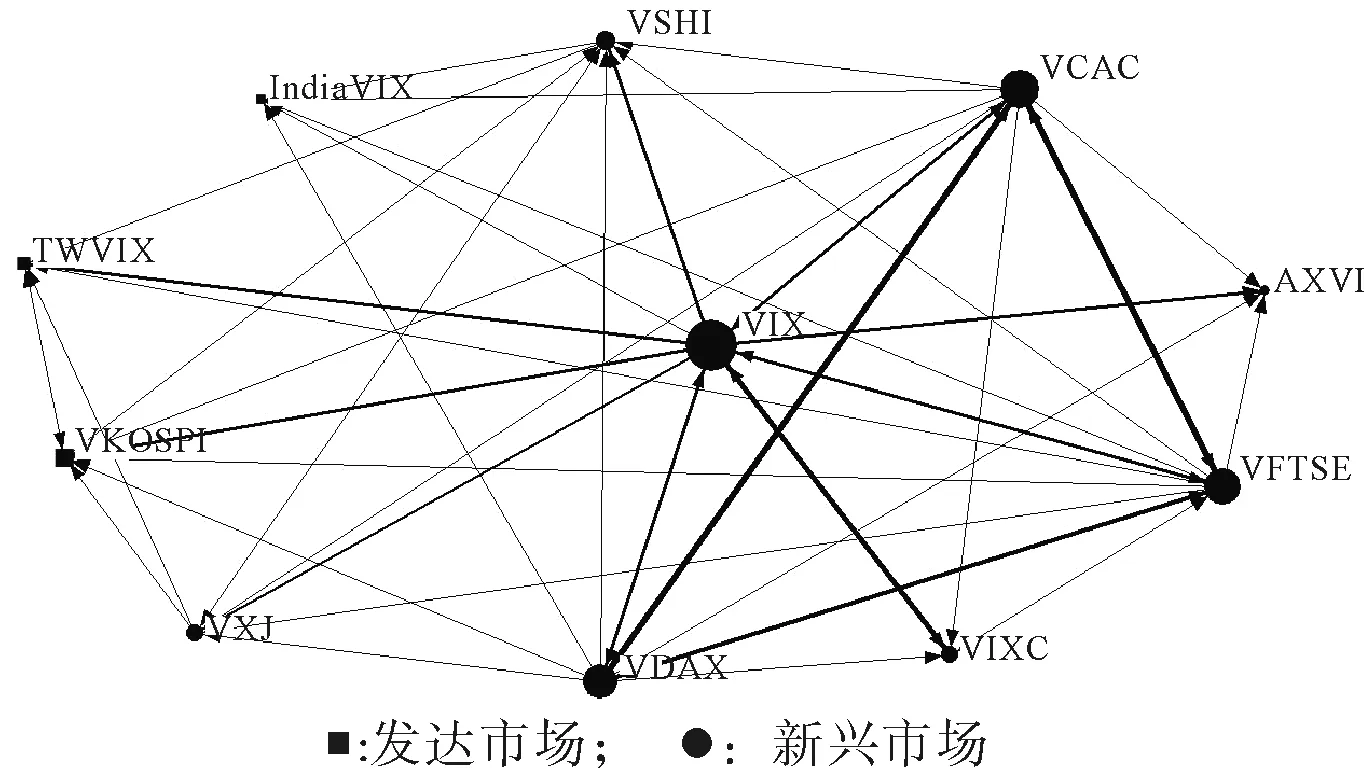
圖1 各市場隱含波動率溢出網絡圖

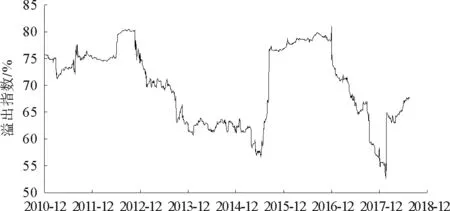
圖2 總波動溢出指數

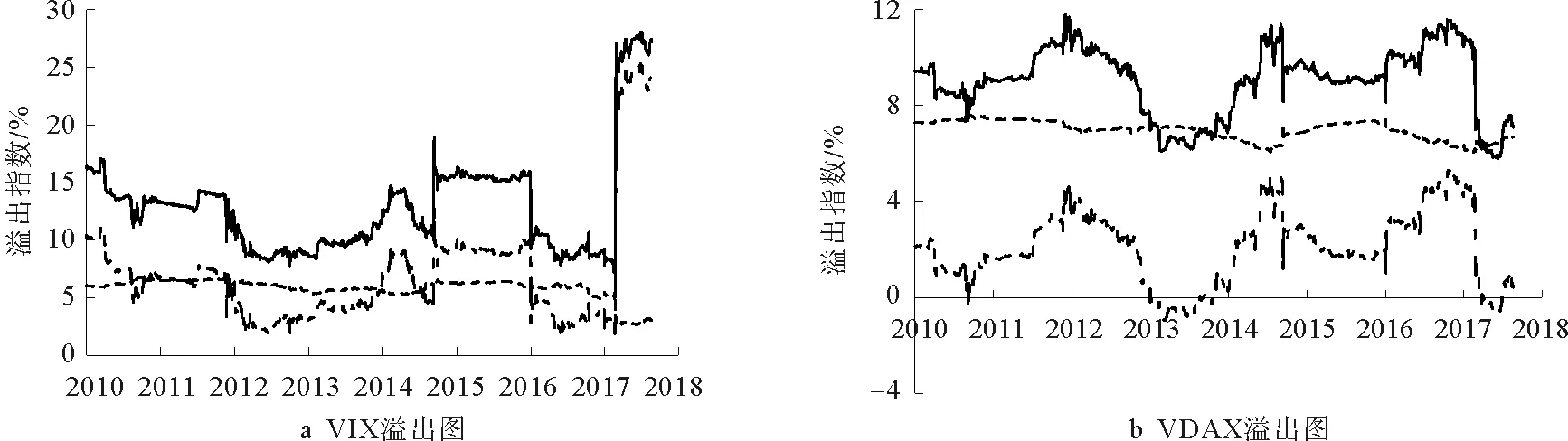
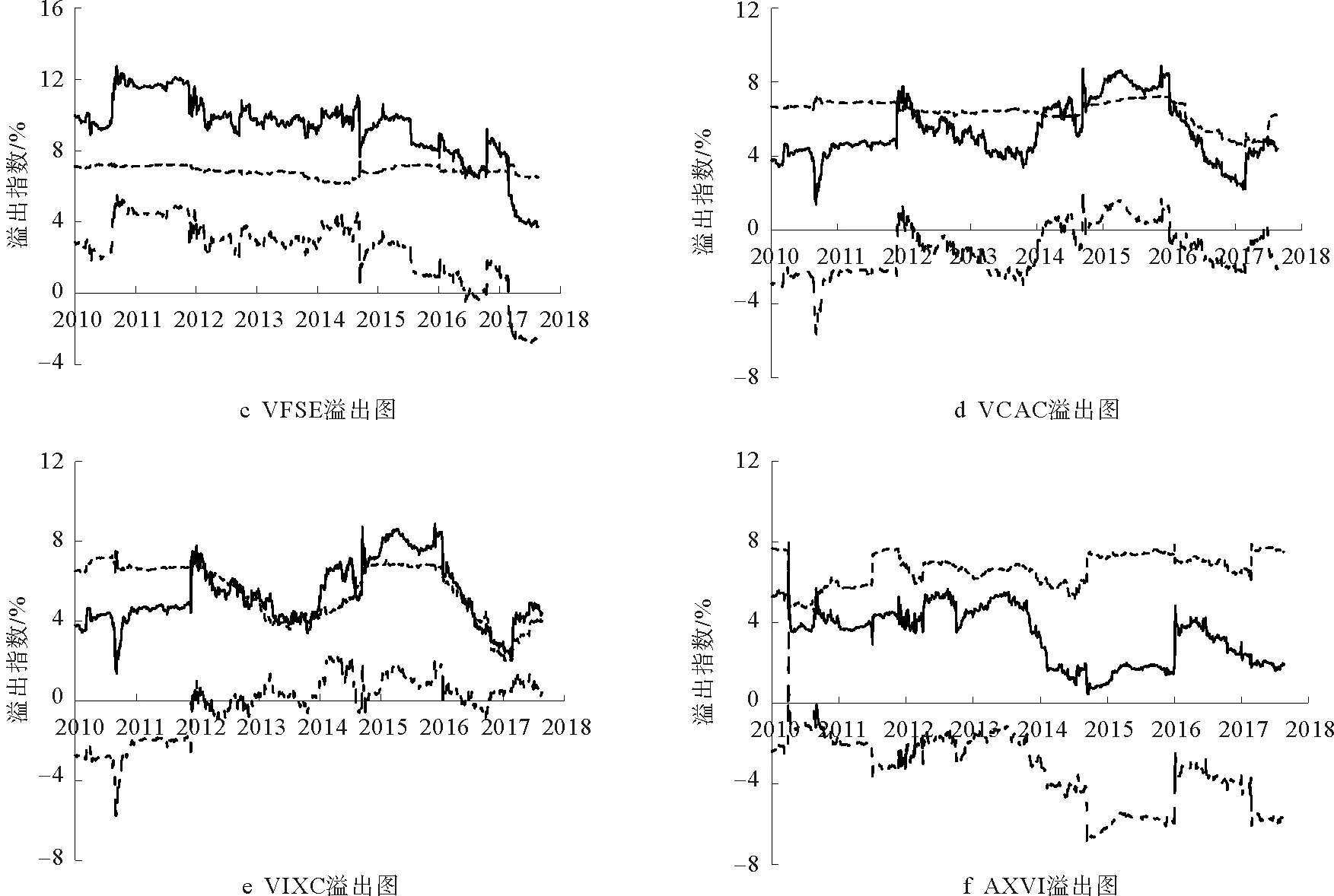
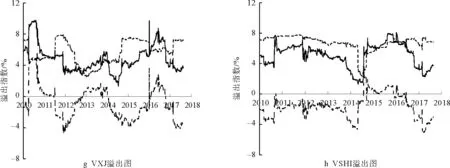
從各個股市波動溢出的溢出、溢入和凈溢出指數來看：美國股市一直表現為溢出強度大于溢入強度，凈溢出效應一直為正，且在2018年年初美股大跌時，VIX的對外溢出指數急劇上升，從7%急劇上升至25%。德國、英國、法國這三個歐洲股市中德國股市的溢出能力較強，凈溢出效應一直為正；其次是英國，而法國較弱，溢出指數在3%至8%之間波動，凈溢出指數有時為正有時為負。英國脫歐期間，歐洲三大股市的反應較為明顯，溢出指數均有明顯上升。加拿大股市也具有一定的對外溢出能力。亞太地區的日本和中國香港在2011年3月日本大地震和2015年7月中國股市大波動反應較為明顯，溢出指數均出現顯著上升。澳大利亞與韓國、印度、中國臺灣這三個新興市場對全球股市的影響較弱，主要表現為凈溢入，即溢入大于溢出，是波動溢出的主要吸引者。

3 影響因素分析

在分析波動率溢出的全樣本結構與動態結構后，一個自然的問題是：什么因素影響了波動溢出？究竟是經濟基礎因素還是市場傳染因素又或者是二者共同作用的結果。為了回答這一問題，我們對波動溢出背后的影響因素進行分析，采用如下的動態面板模型進行回歸：

(8)

其中，Spilloveri,t是基于滾動窗口樣本期計算的第i個市場第t年的波動率對外溢出指數，取波動率對外溢出指數的年內平均值作為該年的觀測值。由于溢出指數存在明顯的序列相關，加入溢出指數的一階滯后項作為解釋變量。α0表示市場固定效應，代表所有不隨時間變化的影響一國對外波動溢出程度的市場特定因素。

選取貿易依存度Tradei,t和資本關聯FDIi,t來反映各經濟體經濟基本面的相互關聯。其中Tradei,t等于經濟體i的進出口貿易總額占同期GDP的比重；FDIi,t等于經濟體i的外商直接投資(Foreign Direct Investment，FDI)流量占同期GDP的比重。某一經濟體的貿易依存度和資本關聯度越高，意味著該經濟體與世界經濟一體化程度越高[3]。除了經濟基本面上的聯系，投資者的情緒和行為也會造成市場價格聯動，引起風險傳染。根據King and Wadhwani[7]的原始模型，反映波動溢出效應的市場傳染是波動率的遞增函數，這意味著，如果觀察到波動率與波動溢出同向變化，則說明市場傳染機制發揮作用。我們選取經濟體i的股票市場波動率Voli,t作為解釋變量，以分析波動率與一國對外溢出強度的關系。Ck,i,t是所選擇的控制變量，包括經濟體i的股票市場市值占所有經濟體市值的比重、經濟體i的經濟風險指數與所有經濟體經濟風險指數均值的差的絕對值、經濟體i的貨幣對美元匯率的波動性，以控制股票市場、經濟狀況以及匯率波動性的影響。宏觀數據來自于Wind、世界銀行和國際貨幣基金組織網站，經濟風險指標來自于ICRG Group。

表4 波動溢出影響因素動態面板估計結果

本文采用系統GMM方法進行參數估計，對得到的回歸結果通過Sargan檢驗判定工具變量的有效性，通過Arellano-Bond AR檢驗判定模型殘差的一階和二階序列相關性。回歸結果如表4所示。其中，Arellano-Bond AR檢驗表明不存在二階序列相關，說明原模型的誤差項不存在序列相關，符合系統GMM的使用條件；Sargan檢驗表明在5%顯著性水平接受所有工具變量都有效的假設，說明模型在整體上顯著。

模型的回歸結果表明：第一，對外溢出指數的一階滯后項回歸系數較大，且顯著為正，說明各經濟體對外波動溢出在時間上的持續性。第二，貿易依存度回歸系數在10%顯著水平上為正，說明經濟體的對外貿易依存度越大，其股市對外風險溢出的強度就越大。資本流動因素回歸系數在10%顯著水平上為負，說明經濟體的資本流動越大，其股市對外溢出的強度越弱。溢出國的FDI流入對溢入國的股市有正面作用，但FDI的流入可能導致其母國的投資額的下降，從而對其股市產生不利影響，因此FDI降低了其對外溢出的能力。第三，市場波動率與對外溢出指數正相關，且系數在10%顯著水平上顯著，說明市場傳染機制起作用。綜上，某一經濟的對外波動溢出是經濟基本面因素和市場傳染機制共同起作用的結果，從回歸系數的大小來看，對外波動溢出主要通過市場傳染進行傳導。

4 結論

隨著經濟和金融一體化的發展，全球金融市場交互關聯成一個錯綜復雜的系統，系統內的各個子市場之間相互影響。因此，準確地衡量所有市場波動溢出的總體效應以及系統內各個子市場的作用，對于識別系統性重要金融市場，防范波動溢出對系統性風險的沖擊具有重要的作用。本文利用溢出指數和網絡分析方法，對美國、英國、法國、德國、澳大利亞、加拿大、日本、中國香港、韓國、印度、中國臺灣等11個國際股市的隱含波動率之間的波動溢出效應進行分析，測度了波動溢出的方向、水平和動態趨勢。使用隱含波動率進行研究，是因為與其他的波動率測度相比，隱含波動率反映了投資者對股指期權標的資產未來波動率的預期，使得結果更具前瞻性和準確性。同時，本文從經濟基礎和市場傳染兩個視角，對波動溢出效應的因素進行了探討。本文的研究為理解股市間金融風險的傳遞結構提供借鑒，為金融監管機構進行有效金融市場監管提供參考。

本文研究的主要結論為：第一，美國股市是全球股市波動溢出網絡的中心，對其他市場存在明顯的波動溢出效應，英國、法國、德國3個市場組成小聚集群體，相互之間存在明顯的波動溢出，但對其他市場的溢出強度較弱，而其他市場是波動溢出的主要吸收者。第二，國際股市間的總波動溢出指數在50%到85%之間波動，整體風險聯動性較強，在金融震蕩時期會顯著上升，并具有一定的持續性。第三，對波動溢出指數的影響因素分析結果表明，經濟基本面和市場傳染機制可以較好地解釋一國股市的對外波動溢出強度，并且市場傳染機制起主要決定作用。

本文結論的政策含義主要體現在以下兩個方面：一是應該充分重視美國股市對全球金融市場的影響。我們的研究表明，后危機時代，美國股市仍是全球波動溢出網絡的中心，對全球金融市場穩定起著重要的作用。隨著我國股市進一步的開放和國際化水平的提升，我們應該高度重視美國股市的不確定和波動對我國股市所造成的輸入型波動沖擊。二是波動溢出效應的存在使得各國金融監管部門有必要提高國際協作、加強政策協調，建議考量將溢出指數納入金融穩定性監測系統。一方面溢出指數給出了溢出的方向和強度，這有利于量化波動溢出的影響；另一方面，金融震蕩時期的，通過溢出指數可以識別并持續跟蹤某個市場的影響，有利于采取針對性措施。