含時滯多智能體系統的邊動態二分一致性

李英楨，紀志堅，劉 帥，楊儀龍

(青島大學自動化學院，山東 青島 266071)

0 引言

多智能體系統研究的熱點問題是其一致性，一致性是一種普遍的群集行為，在自然界中，魚群聚集、鳥類遷徙及螢火蟲同時閃光；在人類社會中，掌聲的同步及人類生物振蕩器的同步都可以歸納為一致性問題。一致性是多智能體實現協同合作共同完成任務的基礎，其在包括群集、分布式計算、傳感器網絡及編隊控制等許多領域都有廣泛應用，如機器人編隊控制、無人機協調控制以及人造衛星控制等。目前關于一致性的研究大多基于個體間的合作關系，然而在實際的問題中，如社會學，飛機編隊，個體間除了合作關系，還常常存在競爭關系。關于多智能體之間的合作關系，最初R.Olfati-Saber在文獻[1]中構造了基礎一致性協議，在連通無向圖下研究了平均一致性問題。之后W.Ren和R.W.Bread在文獻[2]中提到一個解決一般一致性問題的充分必要條件是相互作用的有向圖存在一個生成樹。關于多智能體之間的競爭關系，S.Ermon等人[3]提及的對于自治網絡在工程應用中的事實估計的情況，這種關系可以用符號圖表示，即圖中邊的權重可以是負的，其中正權表示智能體間的合作關系，負權表示智能體間的競爭關系。關于正負混合權重的情形，C.Altanfini在文獻[4]中研究了關于連通符號圖(或強連通符號圖)的二分一致性問題，并證明了在結構平衡的符號(有向)圖下，基礎一致性協議能夠解決二分一致性問題。之后Zhang等[5]研究了系統達到二分一致性的條件，討論了二分一致性和一般一致性之間的等價關系，擴展了基于黎卡提方程的協同跟蹤控制器以解決二分一致性問題。

上述關于二分一致性的結論都是以節點動態來描述，但是在現實生活中，有很多物體，例如道路，電線，甚至個體間的相互關系和作用的實體等并不能簡單地用通常的節點動態來描述，而是用邊動態來描述。拿交通網絡來舉例，用邊動態來描述更合理準確，具體而言，對于單行道，用有向邊來表示，對于雙行道，用無向邊或雙向邊表示，我們期望交通網絡中不存在一些道路擁堵而一些道路冷清的情況，使所有道路的交通狀況能達成一致，即道路交通網達成邊動態一致性。關于邊動態的研究目前很少，Wang等人[6]研究了一階多智能體系統的邊動態一致性問題，在有向圖下建立了邊動態一致性協議，利用了線圖這個工具，解決邊動態問題，并且證實了在強連通有向圖下，多智能體系統能實現邊動態一致性。

此外，實際問題中智能體之間的信息傳遞往往會存在通訊時滯，導致系統的動態特性變差甚至導致系統無法實現穩定性，因而針對含有通訊時滯的多智能體系統的問題研究也受到了廣泛關注。2004年，Saber等人[7]研究了一階動態系統在均勻固定交流時滯下有向網絡的平均一致性問題。之后，Du在[8]中研究了一階多智能體系統在具有正負混合權及通訊時滯的無向拓撲下的二分一致性問題，構造了含不均勻時滯的一致性協議，給出了時滯多智能體系統實現二分一致性的結論。Li等人[9]研究了無向拓撲下一類含有固定時滯的二階多智能體系統的二分一致性問題，其中對于含有交流時滯情形下的一致性及二分一致性問題的分析，借助了一類等價變換，將系統的一致性問題等價為穩定性問題。2018年，Tian在[10]中研究了二階時滯系統正負混合加權的系統二分一致性問題，利用矩陣論的方法對二階系統進行降階處理，簡化分析。上述關于符號圖下系統的二分一致性都是在結構平衡這個條件下得到，2017年Jiang在[11]中對非結構平衡條件下系統的二分一致性進行了研究，并設計了不需要整個拓撲圖信息的完全分布式控制器。目前對時滯系統的穩定性分析主要有兩類方法，一類是頻域方法，如[12]、[13]，主要研究系統傳遞函數，一類是時域方法，如[14]、[15]，主要研究系統狀態方程。對于含不均勻時滯的多智能體系統，通常采用時域法利用Lyapunov穩定性理論進行處理。其中[16]詳細說明了Matlab中的LMI(線性矩陣不等式)工具箱，據此可以解決由Lyapunov方程產生的線性矩陣不等式的求解問題。

在上述工作的基礎上，本文基于邊動態重新設計了一階和二階系統模型的二分一致性協議，使系統在實現二分一致性時系統各邊狀態趨于模相等。在考慮邊動態時，利用線圖這一工具，將系統模型的邊動態轉化為節點動態，之后在研究二分一致性問題時利用規范變換將其等價為普通的一致性問題，并通過矩陣變換將多智能體系統的一致性問題等價為穩定性問題，利用邊與節點之間的轉化關系分別得到一階、二階系統實現邊動態二分一致性的充分條件。與[4]不同，由于在實際多智能體網絡中，信息在傳遞過程中存在著不同的損耗和時滯，因此，本文在上述邊動態二分一致性的基礎上，進一步在協議中加入了不均勻的通訊時滯。在解決含時滯系統的二分一致性問題時，在上述穩定性問題的基礎上，利用Lyapunov漸近穩定性理論，構造含時滯信息的Lyapunov-Krasovskii泛涵，并對泛函進行求導，在求解Lyapunov-Krasovskii泛涵時，本文利用Matlab中的LMI工具箱對其進行處理，利用gevp求解器解出滿足系統穩定時的最大通訊時滯，進一步得到含時滯多智能體系統實現邊動態二分一致性的充分條件。

本文的結構如下安排：第2節介紹了線圖、結構平衡等相關圖論知識以及邊動態下的一階(二階)系統的二分一致性協議；第3節給出了關于一階(二階)系統關于二分一致性的結論及證明；第4節針對上章結論分別進行了仿真，并給出了仿真結果；第5節總結了本文所做工作。

1 預備知識

1.1 圖論

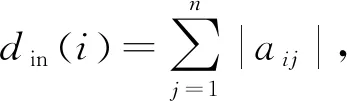
1.1.1 結構平衡

定義1結構平衡：如果強連通的有向圖的所有的環都是正的，那么它是結構平衡的。換一種說法，如果強連通的有向圖的節點都可以被分為V1,V2，其中V1∪V2=V,V1∩V2=φ且aij≥0,?i,j∈Vp,(p∈{1,2}),aij≤0,?i∈Vp,j∈Vq,(p,q∈(1,2),p≠q)，則其是結構平衡的。否則，稱為結構不平衡。

引理1[4]當且僅當以下等式成立，對邊符號對稱的強連通有符號的有向圖G(A)結構平衡：

1)G(A)的所有有向環均為正；

2)?D使得DAD所有的元素都是正的；

3)0是L的特征值。

推論1當且僅當0是拉普拉斯矩陣L的單特征值，也就是說rank(L)=n-1，對邊符號對稱的強連通的有符號有向圖G(A)是結構平衡的。

1.1.2 線圖

n個節點m條邊的有向圖G={V,E,A}，其線圖L(G)定義為[6]：

1)L(G)中的節點(i,j)對應于G中的有向邊(i,j)；

2)對于G的節點i，在線圖L(G)中其入邊(i,j)與其出邊(k,i)相鄰，其中i,j,k=1,2,…,n。

值得注意的是，我們在符號的有向圖及其線圖中有以下規則：

1)從原始圖的負加權入邊生成的線圖中的邊取負權重；

2)從原始圖的正加權入邊生成的線圖中的邊取正權重。

注：虛線表示負邊，實線表示正邊圖1 原始有向拓撲圖和邊轉化為節點后的線圖

關于原始拓撲圖及其線圖有如下引理：

引理2[10]如果有向圖G包含超過一個節點且是強連通的，則其線圖L(G)也是強連通的。

引理3[10]當且僅當G是結構平衡的，對于強連通的對邊符號對稱有符號有向圖G，其線圖L(G)是結構平衡的。

1.2 一致性協議

假設多智能體系統有n個多智能體，這n個多智能之間有M個邊，用邊動態來表示多智能體之間的連接關系：

(1)

(2)

上述(1)為一階系統模型，(2)為二階系統模型，其中xij(t)∈R表示邊ij的狀態，vij(t)∈R表示邊ij的速度，uij(t)∈R表示邊ij的控制協議或輸入。為了方便描述，下面的敘述中在不引起混淆的情況下省略時間變量t，例如uij(t)寫成uij。

(3)

其中，c為任意常數，則稱該系統可以實現邊動態二分一致性。

對于系統(2)，其實現邊動態二分一致性時，各邊狀態如下：

(4)

對于二分一致性問題(3)、(4)，在多智能體系統(1)、(2)不受通訊時滯影響的情況下，考慮其一致性控制協議分別為：

(5)

(6)

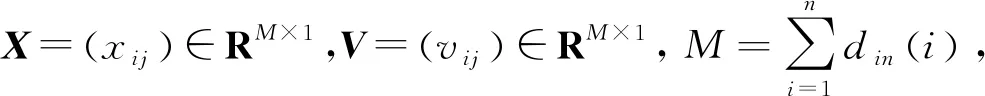
(7)

基于L′=[l′ij]M×M=C′-A′可知，將協議(5)、(6)分別用于系統(1)、(2)，可得：

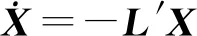
(8)

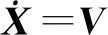
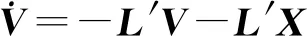
(9)

在實際應用中，各智能體間的信息傳輸往往不可避免地存在著通訊時滯。為了解決通訊時滯問題，我們在一致性協議(5)、(6)中分別加入不均勻通訊時滯得到如下協議：

(10)

(11)

其中,τij表示第i個智能體獲得第j個智能體狀態信息時存在的通訊時滯,對于邊動態系統，由于研究對象是圖的邊，而時滯信息主要存在于邊上，因此將原始拓撲圖轉化為線圖之后，其線圖的邊并不存在時滯，時滯信息儲存在線圖的節點中，我們做出如下定義:

定義2線圖中節點之間的時滯由發送信息的節點(即圖1b的非箭頭端節點)確定。

由于不同智能體之間的通訊距離不一定相同，設多智能體系統中不同的通訊時滯個數為m，其中m≤M,記第k個通訊時滯為τk,k∈{1,2,…,m}，并且令0<τ1<τ2<…<τm≤d，其中，d為通訊時滯上界。那么將協議(9)，(10)分別用于系統(1)，(2)可得如下模型：

(12)

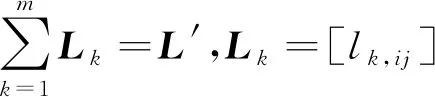
其中，N(k,i)={j|j≠i,τij=τk}。

2 主要結論

2.1 一階無時滯系統的邊動態二分一致性

首先，引入一類正交矩陣D，其定義為:D={diag(σ),σ=[σ1,σ2,…,σn],σi∈{-1,1}}其中，D滿足DTD=DDT=I(單位陣)，并且D-1=D。

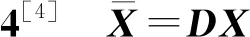
(13)

其中，常數c′滿足|c′|=|c|。

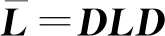
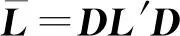
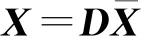
(14)

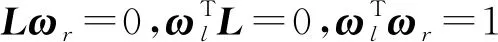
(15)

基于上述二分一致性條件(3)并根據引理4，容易看出一致性等價地表示為

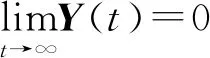
(16)

即多智能體系統的一致性問題可以轉換成一個關于Y的穩定性問題。由(9)可得：

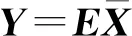
(17)

(18)

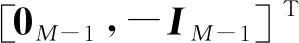
(19)

(20)

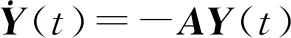
(21)

根據上述描述，可以得到以下結論。

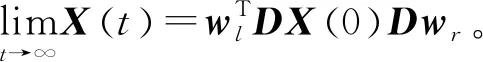
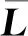
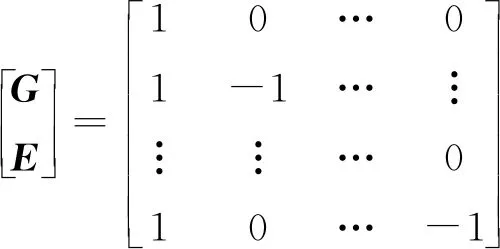
對H求導如下：

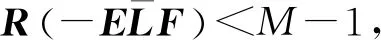
2.2 一階含時滯系統的邊動態二分一致性

引理7[17]設x,y為任意n維實向量，H為n×n維可逆對稱矩陣，則下面的矩陣不等式成立：

2xTy≤xTH-1x+yTHy

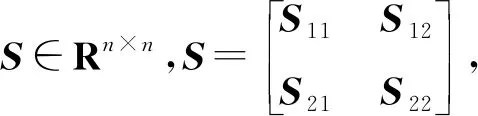
1)S<0；

對一階多智能體系統存在通訊時滯的情形，類似于式(20)的建立，我們由式(11)可得：

(22)

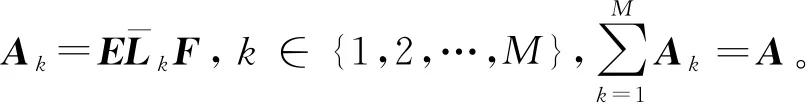
定理2對于一個有向強連通圖G(A),如果G(A)是結構平衡的。假設存在m個固定時滯τk，當存在對稱正定矩陣P,Qk,Wk∈R(M-1)×(M-1)，k∈{1,2,…,M}使下面式子成立：

(23)

(24)

那么，一階含時滯多智能體系統能夠實現邊動態二分一致性。

證明：構造Lyapunov-Krasovskii泛函：

V(t)=V1(t)+V2(t)+V3(t)

其中：

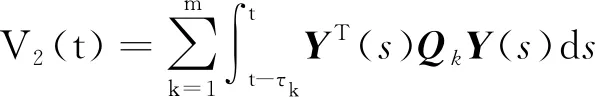
對V(t)求導可得：

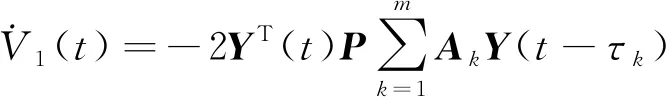
由Newton-Leibniz公式和引理8可知：

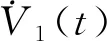
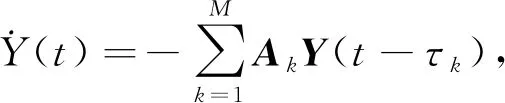
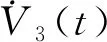
得到：

其中,

(25)

(26)

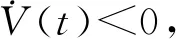
2.3 二階無時滯系統的邊動態二分一致性

如同一階系統，二階系統經規范變換之后模型如下：

(27)

其中,

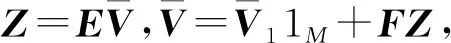
如一階模型分析可得如下結果：

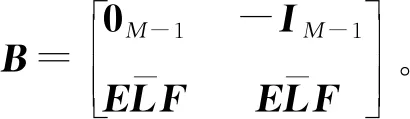
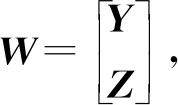
(28)

(29)

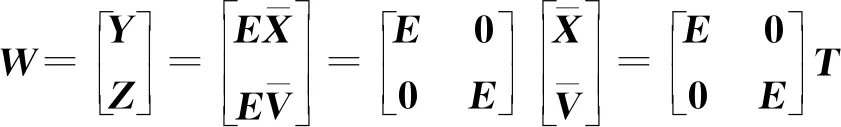
(30)

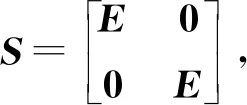
2.4 二階含時滯系統的邊動態二分一致性

將協議(10)代入到(28)中可得到如下系統模型：

(31)

類似一階系統，將上述模型轉換為式(20)的形式，則轉換之后的系統模型如下：

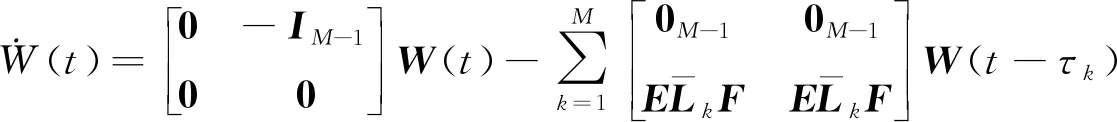
(32)

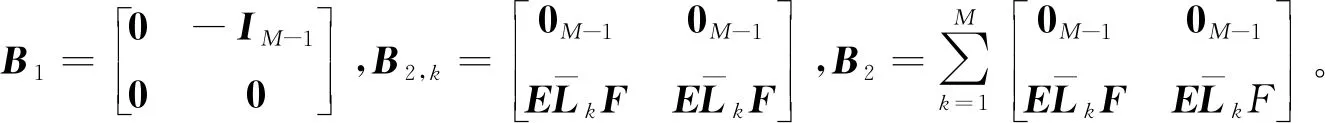
證明：

必要性：根據W的定義，顯然必要性成立，即二階系統實現二分一致性時降階系統的每個解均趨于0。

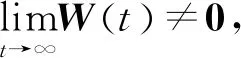
根據上述分析，可以將一致性的證明轉化為對轉換系統的漸近穩定性的證明。

定理4在協議(10)下，對于給定的最大通訊時滯d，如果存在正定對稱矩陣P,Qk,Rk使下式成立：

(33)

那么系統(2)能實現邊動態二分一致性。其中：

(34)

證明：同上述一階系統，選取如下Lyapunov-Krasovskii泛函：

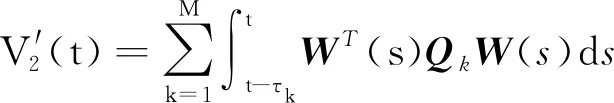
其中P,Qk,Rk定義如上文所述，分別求導后結果如下：

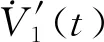
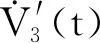
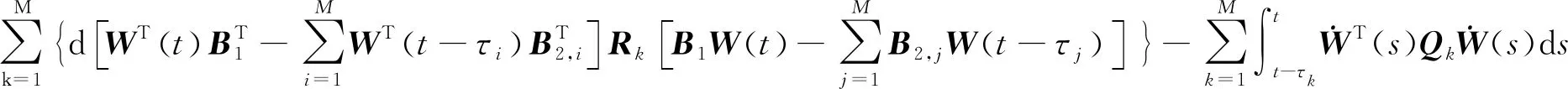
將上述泛函整理成矩陣形式：

(35)

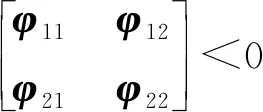
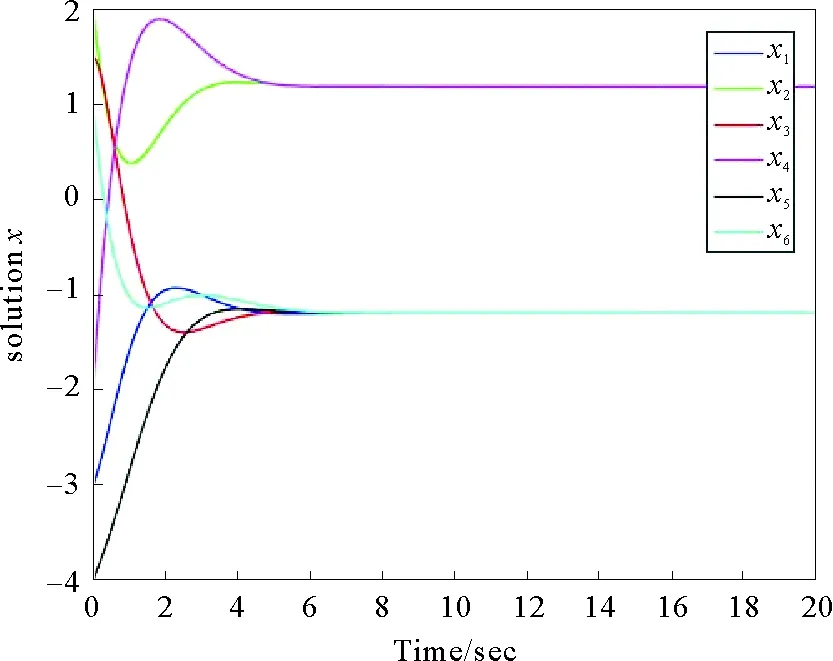
圖2 無時滯情況下一階系統的邊動態二分一致性情況

3 仿真

3.1 無時滯多智能體系統的邊動態二分一致性仿真

考慮由5個節點構成的多智能體系統，其有向拓撲連接如圖1a，其中實線表示個體之間的合作關系，權重取+1，虛線表示的是個體之間的競爭關系，相應的權重取-1。將其轉化為線圖之后，其對應的邊動態有向拓撲圖如圖1b所示，可以看出原始拓撲圖和線圖均為強連通，并且都是結構平衡的。考慮一階系統模型(1)，取各邊初始狀態為：x21=-3,x13=2,x34=1.5,x45=-2,x52=-4,x42=1。其仿真結果如圖2所示，可以看出當系統中不存在時滯時，對邊符號對稱的一階強連通有向多智能體系統能實現邊動態二分一致性。進一步考慮二階系統模型(2)，取各邊初始狀態為：x21=-3,x13=2,x34=1.5,x45=-2,x52=-4,x42=1，v21=2,v13=-1,v34=-3,v45=7,v52=6,v42=3。其仿真結果如圖3所示，可以看出二階強連通有向多智能體系統也可實現邊動態二分一致性。

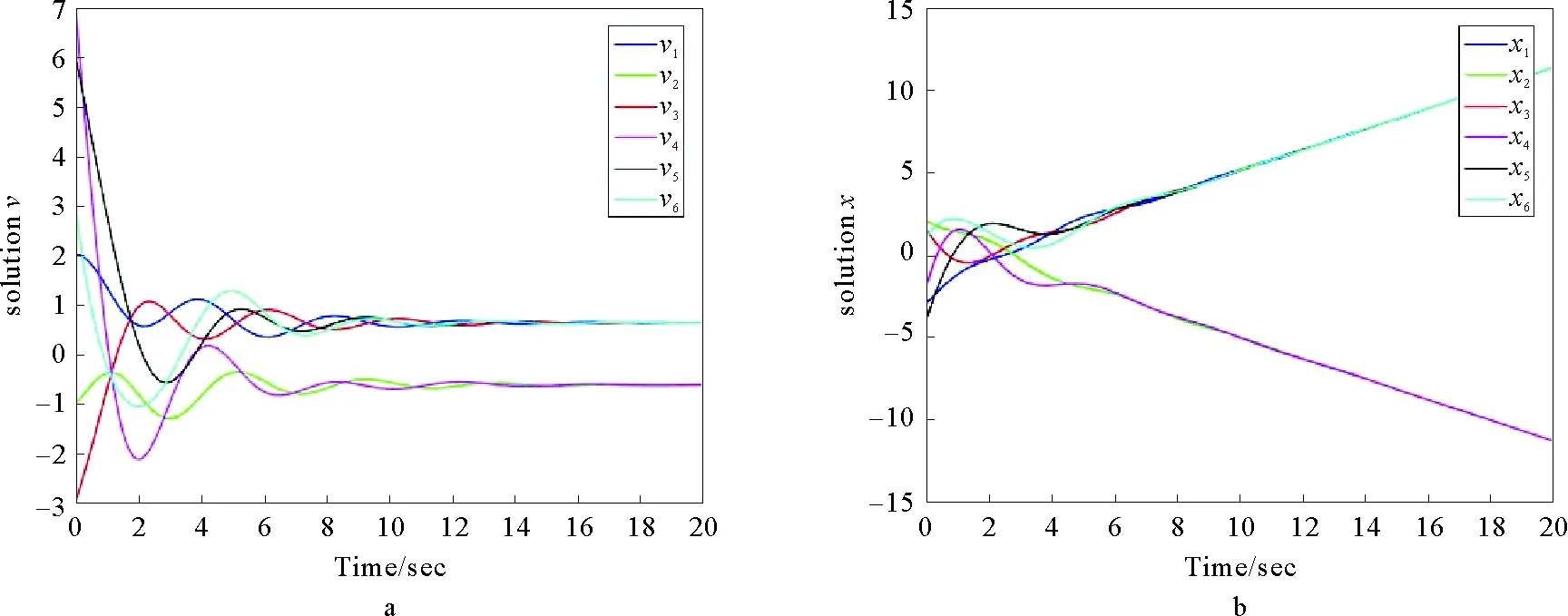
圖3 無時滯情形下二階系統的邊動態二分一致性仿真

3.2 含時滯多智能體系統的邊動態二分一致性仿真

考慮將時滯加到多智能體系統中，對系統(1)進行分析,利用控制協議(9),同樣選取圖1a為系統的拓撲結構，取系統的6個邊的初始狀態為：x21=-3,x13=2,x34=1.5,x45=-2,x52=-4,x42=1，根據式(22)和式(23)可求得通訊時滯上界d=0.555 3，在通訊時滯上界的范圍內，我們選取τ21=0.455 3,τ13=0.355 3,τ34=0.255 3,τ45=0.155 3,τ52=0.055 3,τ42=0.555 3，作為對照，另選取一組時滯使其超過通訊時滯上界τ21=0.855 3,τ13=0.553,τ34=0.7,τ45=0.6,τ52=0.055 3,τ42=0.555 3，仿真結果如圖4所示，圖4a表明在不超過通訊時滯上界的前提下，對邊符號對稱的強連通有向圖加入時滯后依然可以實現邊動態二分一致性，圖3b表面當邊緣時滯超過了通訊時滯上界后，系統無法再實現邊動態二分一致性。進一步考慮二階系統模型(2),采用式(10)表示的控制協議，根據式(30)可求得通訊時滯上限d=0.146 0,在通訊時滯上界的范圍內，我們選取τ21=0.146 0,τ13=0.106 0,τ34=0.046 0,τ45=0.086 0,τ52=0.076 0,τ42=0.026 0，仿真結果如圖5所示。

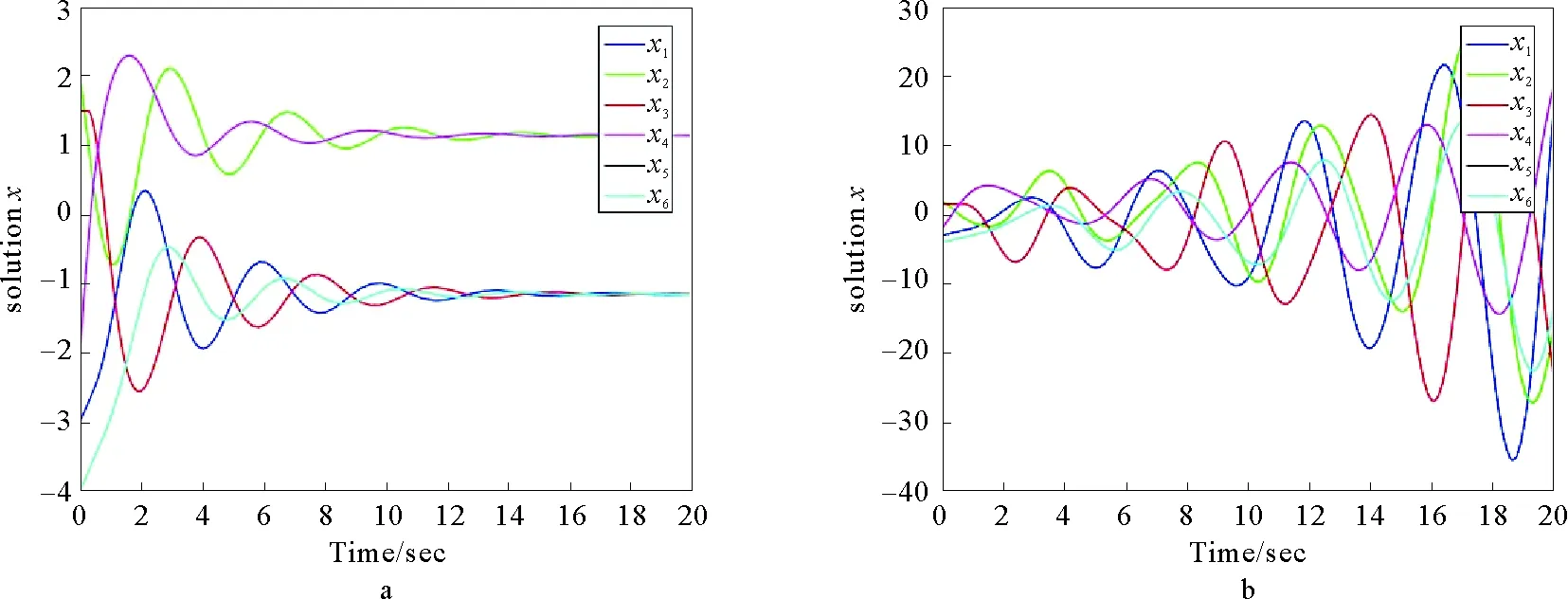
圖4 含時滯一階系統的邊動態二分一致性仿真

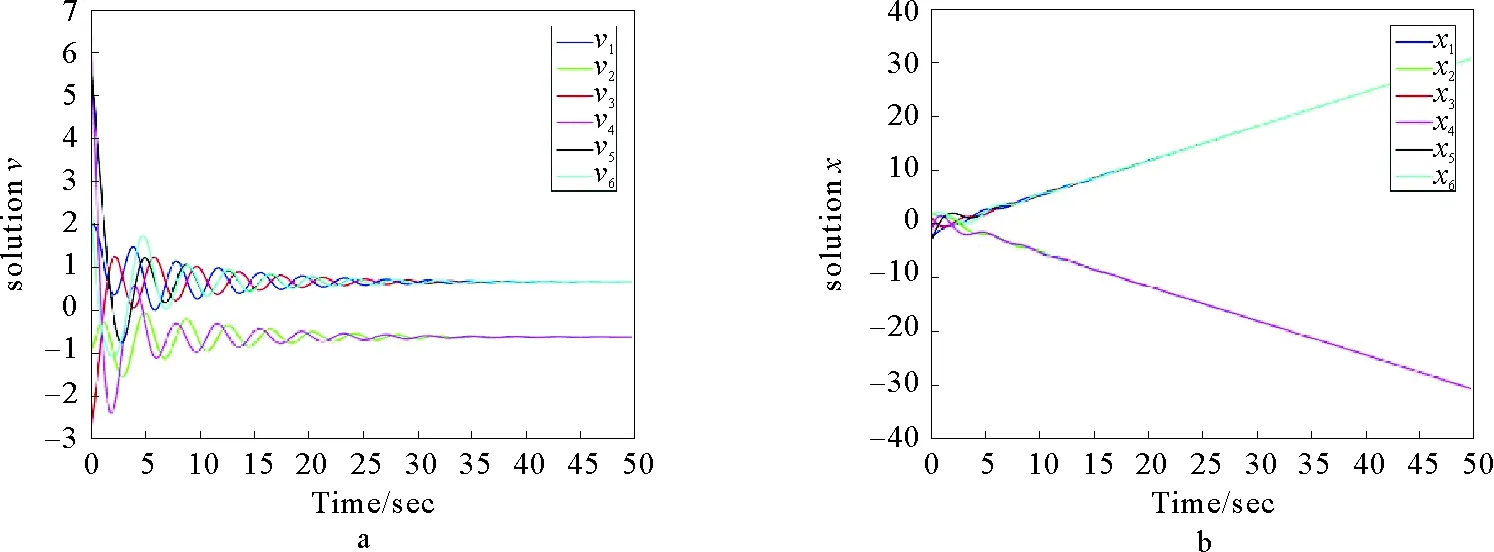
圖5 含時滯二階系統的邊動態二分一致性仿真

4 總結

本文基于邊動態分別設計了無時滯和含時滯多智能體系統的二分一致性協議，研究了對邊符號對稱的強連通有向圖下的多智能體系統的邊動態二分一致性問題。分別針對一階和二階系統給出證明，得到系統在無時滯和含時滯情況下實現邊動態二分一致性的充分條件，并利用Matlab進行數值仿真驗證方法的合理性。最后本文的結論仍在結構平衡這個限制條件下得到，未來的研究重點是打破這個限制條件。