一種人工魚群蛙跳混合優化算法

姜慧楠， 張向鋒

(上海電機學院 電氣學院, 上海 201306)

人工魚群算法(Artificial Fish Swarm Algori-thm, AFSA)，是一種根據魚群覓食行為的優化算法[1]。算法以模仿自然界的魚群尋食過程來求得問題的最優解，它最初的收斂速度較快，但是后期收斂速度慢，因此，適用于精度要求不高的尋優問題[2-3]。蛙跳算法(Shuffled Frog Leaping Algori-thm, SFLA)是一種新的結合了全局搜索和局部更新的元啟發式協同搜索算法[4]。SFLA求解速度快且全局尋優能力強，但存在前期收斂速度慢的問題。

AFSA因具有收斂速度快、計算原理簡單等優勢，得到了國內外學者的廣泛關注。文獻[5]對適應度值最好的人工魚利用最速下降法進行更新，提高魚群的整體水平；文獻[6]采用引入對稱正態隨機行為及自適應調整行為參數，使得系統的收斂速度更佳；文獻[7]驗證了一種基于DNA改進的AFSA；文獻[8]將禁忌搜索策略融入到AFSA尋優過程中，并在求解車間調度問題中取得了比較好的結果；文獻[9-10]采用對魚群行為的改變，提高了AFSA的搜索速度。文獻[11-12]為克服SFLA存在的問題，對全局及局部做出改進，提出一種改進的SFLA；文獻[13-14]通過對步長公式的改變及引入影響因子的方法，提升了SFLA的搜索能力；文獻[15-16]通過借鑒優化及搜索策略的思想，使得最差青蛙的位置趨向最佳，提高了SFLA搜索的速度。

針對SFLA在后期收斂速度慢、易陷入局部最優和精度低等問題，本文將結合AFSA前期收斂速度快和SFLA局部搜索能力強的優勢，通過將兩種仿生算法聯合運用，提出一種人工魚群-蛙跳混合優化算法(Artificial Fish Swarm Algori-thm-Shuffled Frog Leaping Algorithm, AFSA-SFLA)。

1 人工魚群算法及蛙跳算法

1.1 AFSA基本原理

魚群的主要行為包括魚群初始化、覓食行為、聚群行為、追尾行為、隨機行為[17]。其主要行為如下：

(1) 魚群初始化。魚群中的每一條人工魚是在給定范圍內產生的隨機數組。

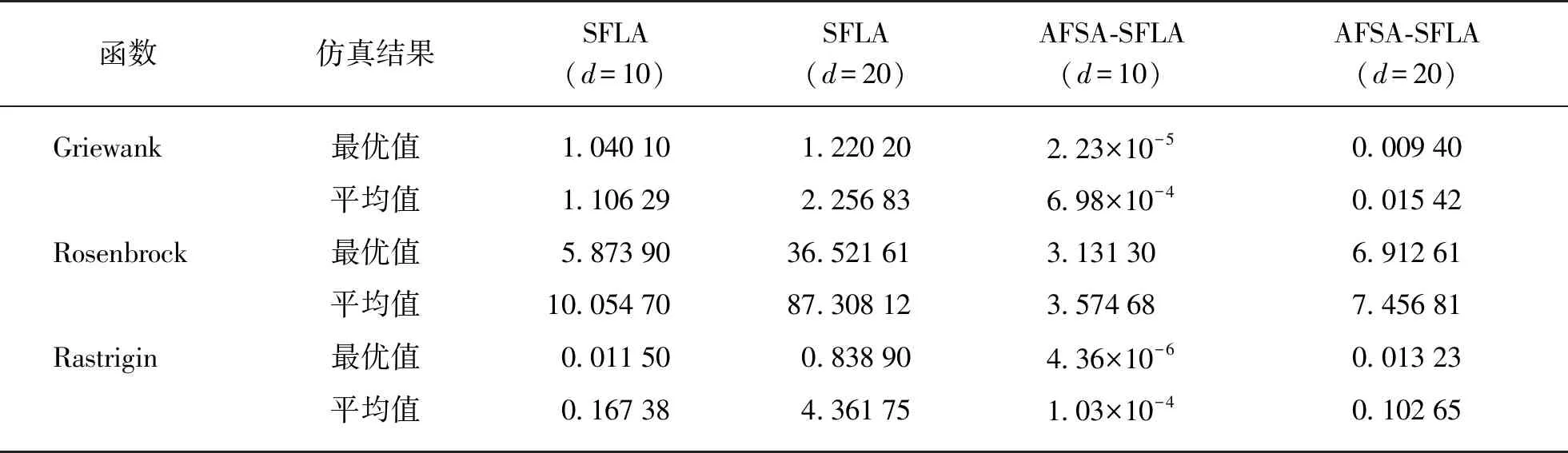
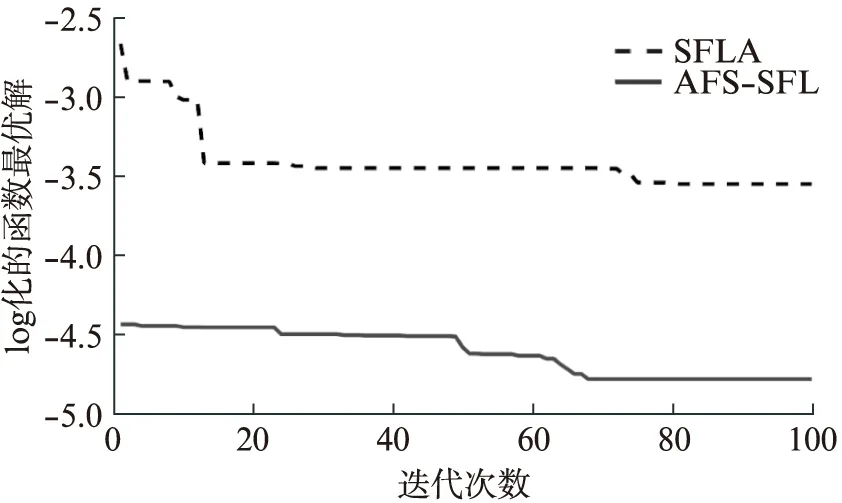
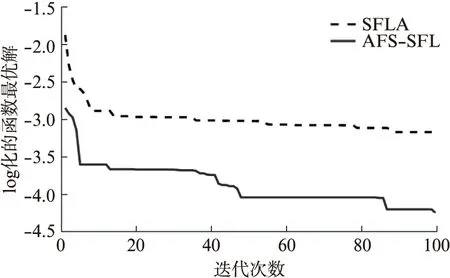
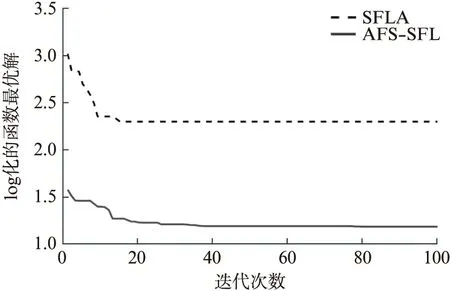
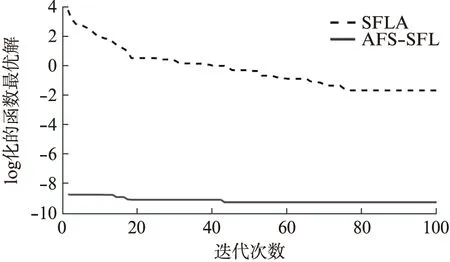
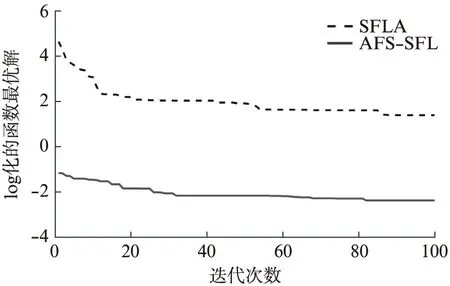
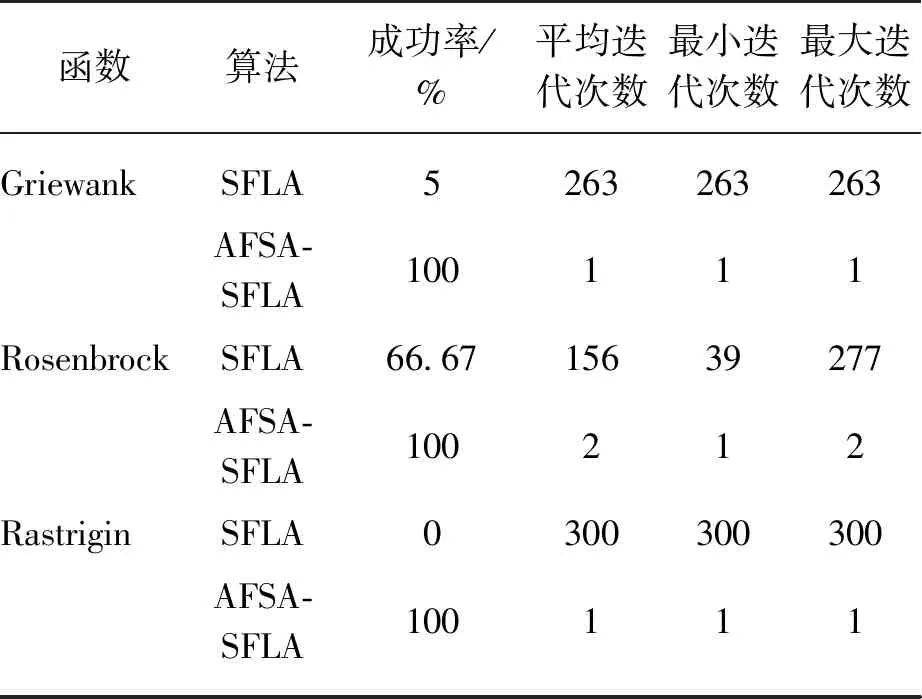
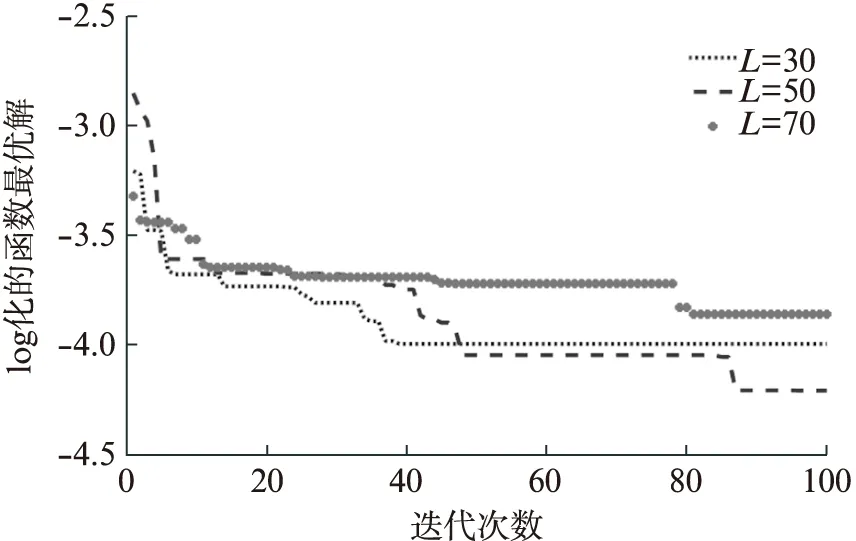
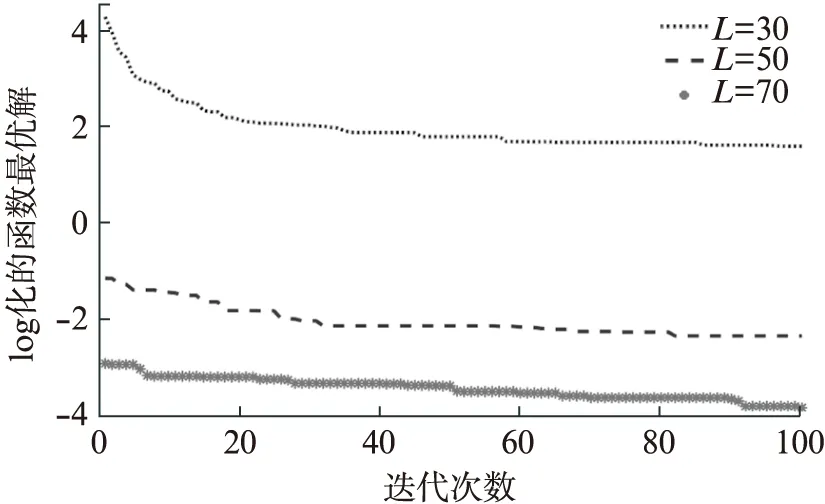
(2) 覓食行為。假設當前人工魚的狀況為Xi，在其感知的范圍內隨機選擇一個狀況Xj，如果求極大值問題，Yi為第i條人工魚當前所在食物濃度(Yi

(3) 聚群行為。設當前人工魚的狀況為Xi，探究當前領域內(即di，jδYi(δ為擁擠度)，說明同伴中央有較多的食物且不太擁擠，則朝同伴中央的位置行進一步，否則實施覓食行為。

(4) 追尾行為。設當前人工魚的狀況為Xi，試探當前領域內(即di，jδYi，說明同伴Xj的狀態有較多的食物且不太擁擠，則朝同伴的Xj的位置行進一步，否則實施覓食行為。

(5) 隨機行為。隨機行為的實現比較簡單，就是在視線中隨機抉擇一個情況，然后向該方向行進，即Xi的下一個動作為

X′i=Xi+r·V

(1)

式中：r是[-1，1]區間的隨機數。

1.2 SFLA基本原理

SFLA是模擬青蛙在尋食的過程當中，青蛙群體通過按子群分類進行信息交換的進展，將全局搜索與子群局部搜索相結合，使算法朝著全局最優解的方向進化[18]。

(1) 全局搜索。全局搜索的布置如下：① 設置SFLA參數種群分組數m，每組青蛙包含的青蛙個數n，組內迭代次數Ne，最大、最小步長分別為swmax、swmin，種群總的進化代數N′max，青蛙位置的最大、最小值分別為Pmax、Pmin；② 隨機初始化青蛙的種群，共生成F只青蛙，簡記為P={P1，P2，…，PF}，其中Pi代表第i個解(0≤i≤F)，Pi={Pi1，Pi2，…，Pid}，d為解的維數，每一只青蛙代表著一種可行的解；③ 設Ff(Pi)為適應度函數，計算P中的每一只青蛙的適應度值，并將其進行降序處理，同時將第一個適應度值所對應的Pi記錄為全局最優青蛙gx，并將排序后的青蛙放置P中；④ 將P中的F只青蛙，分成m組，每一組包含n只青蛙。將P中第1只青蛙放置第一組，依次第m只青蛙放置第m組。第m+1只青蛙放置第1組，依次第m+m只青蛙放置第m組，依次共循環n次，F只青蛙分組完成；⑤ 每個子群執行子群局部搜索，具體步驟見局部搜索；⑥判別是不是達到了最大迭代次數N′max，若達到了則算法結束，反之，重新混合所有的青蛙，執行步驟③。

(2) 局部搜索。局部搜索的布置如下：① 設j=1，用于記錄每組內的迭代次數；② 關于每一組青蛙適應度值按降序排序，pb代表著每一組的最優青蛙，pw代表著每一組的最差青蛙；③ 組內更新，利用式(2)計算最差青蛙的移動步長sw1，若Ff(pwnew)>Ff(pwold)，執行步驟⑥，否則執行步驟④；

sw1=r·(pb-pw)swmin≤sw1≤swmax

(2)

pwnew=pwold+sw1

(3)

④ 全局最優更新。利用式(4)計算最差青蛙的移動步長sw2，若Ff(pwnew)>Ff(pwold)，執行步驟⑥，不然執行步驟⑤；

sw2=r·(gx-pw)swmin≤sw2≤swmax

(4)

pwnew=pwold+sw2

(5)

⑤ 隨機更新。利用式(6)計算最差青蛙的移動步長sw3；

sw3=Pmax·r(1，d)swmin≤sw3≤swmax

(6)

pwnew=pwold+sw3

(7)

⑥ 將pwnew代替pwold，判別j>Ne是否成立，若成立則一組的局部搜索完成，反之，j=j+1，執行步驟②。

圖1 混合算法流程圖

2 人工魚群蛙跳混合優化算法

針對AFSA和SFLA算法優缺點，本文提出一種AFSA-SFLA，該算法首先采用AFSA收斂速度快的優勢快速尋找到待求解參數全局最優解所在區域。后期為SFLA利用前期AFSA的迭代結果，進行SFLA的初始化。AFSA-SFLA的具體流程如圖1所示。具體步驟如下：① 設定主要初始參數，在給定的規模內初始化魚群；②i=1作為一個循環變量來循環記錄人工魚的個數，人工魚的數目為N；③ 魚群執行聚群行為得到(X1，Y1)，執行追尾行為得到(X2，Y2)；④ 若Y1>Y2則Xi=X1，不然Xi=X2；⑤ 判別i>N是否成立，若成立執行步驟⑥，不然i=i+1，執行步驟③，gen=gen+1；⑥ 判別gen>Nmax是否成立，若成立則執行步驟⑦，反之，執行步驟②；⑦ 切換至SFLA，采用AFSA的最后一次迭代產生的人工魚群進行SFLA的初始化，設置SFLA參數種群分組數m、每組青蛙包含的青蛙個數n、組內迭代數Ne、最大步長swmax、種群總的進化代數N′max，青蛙位置最大、最小值分別為Pmax、Pmin，循環變量ii=1。其中特意要說明的是初始化青蛙種群時，將AFSA迭代后的結果，取占取青蛙種群個數的L倍賦值給青蛙種群(0N′max是不是成立，若成立則輸出參數最優值，不然ii=ii+1執行步驟⑧。

3 仿真實驗與分析

本文采取Rastrigin函數、Griewank函數和Rosenbrock函數作為基準函數，這3個函數都具有數個局部最小值點和一個全局最小值點，可以很好地測驗算法規避局部極值搜索全局最優的能力，標準測試函數如表1所示。

3.1 參數設置與測試函數

實驗中主要參數設置如下：人工魚的數目fishnum=100，最多試探次數try_number=100，最大步長step=0.1，蛙跳組內迭代次數Ne=25，種群分組數m=10。本實驗的仿真軟件如下：Intel i3 CPU 2.40 GHz，RAM 4.00 GB，Window 2007操作系統，MatLab2016b。

表1 標準測試函數

3.2 仿真結果分析

3.2.1 固定迭代次數下算法求解精度對比 采用不同的維數d消除算法的隨機性干擾，在維數d為10和20時，對每一個測試函數分別用SFLA、AFSA-SFLA各自進行20次實驗，仿真結果如表2所示。圖2～圖7為3個基準測試函數在不同維數下的優化結果圖，其中橫軸為迭代的次數，縱軸為log化的函數最優解。

表2 3種基準測試函數仿真數據結果

圖2 Griewank函數在d=10時的進化曲線

圖3 Griewank函數在d=20時的進化曲線

圖4 Rosenbrock函數在d=10時的進化曲線

圖6 Rastrigin函數在d=10時的進化曲線

圖7 Rastrigin函數在d=20時的進化曲線

由表2可以看出，當維數d相同時，AFSA-SFLA的尋優結果優于單獨SFLA的尋優結果。當維數d由10增大至20時，對Griewank函數，SFLA平均尋優結果由1.106 29增大至2.256 83，增大了2.04倍，AFSA-SFLA平均尋優結果由0.000 70增大至0.015 42，增大了22倍。當維數d由10增大至20時，對Rosenbrock函數，SFLA平均尋優結果由10.054 70增大至87.308 12，增大了8.6倍，AFSA-SFLA的平均尋優結果由3.574 68增大至7.456 81，增大了2.08倍，說明AFSA-SFLA相對SFLA對該函數的維數適應性更好。當維數d由10增大至20時，對Rastrigin函數，SFLA平均尋優結果由0.167 38增大至4.361 75，增大了26倍，AFSA-SFLA的平均尋優結果由1.03×10-4，增大至0.102 65，增大了996倍，雖然AFSA-SFLA增大的倍數較大，但是AFSA-SFLA的求解精度優于SFLA的求解精度。

由圖2可知，對于Griewank函數，SFLA在后期迭代效果比較明顯，前期迭代的效果不佳，AFSA-SFLA相對SFLA能快速地在其前期找到可行解，并于迭代70次左右收斂。由圖4和圖5可知，對于Rosenbrock函數在維數為20時，SFLA的平均尋優曲線接近直線，開始就陷入局部最優，全局尋優能力不強。由圖6和7可以看出，對于Rastrigin函數，AFSA-SFLA在前期尋優結果明顯，SFLA收斂慢且平均尋優結果遠大于AFSA-SFLA的尋優結果。

綜合圖2～7可知，SFLA的尋優結果要遠小于AFSA-SFLA的尋優結果，且在高緯數時更易陷入局部最優解，而AFSA-SFLA能更快地找到全局最優解所在的區域，迭代速度快，尋優結果更佳。需要指出的是AFSA-SFLA前段使用AFSA，并將AFSA最后一次迭代產生的人工魚群按照適應度值大小降序排列，取前一定比例賦值給青蛙種群，使得青蛙種群更接近最優范圍，因而其收斂曲線在前期能快速的找到最優解所在的區域，且迭代較為緩慢。

3.2.2 指定精度下算法迭代次數對比 表3為AFSA-SFLA在指定精度下求解基準函數迭代次數的對比，其中成功率是指算法達到指定求解精度的實驗次數除以總實驗次數20。Griewank函數、Rosenbrock函數、Rastrigin函數指定精度分別為10-1、10、10-1，最大迭代次數為300次，即算法迭代300次仍未達到指定精度時，表示迭代失敗。

表3 指定精度下算法迭代次數對比

從表3中可以看出，在指定收斂精度下，對Griewank函數SFLA算法達到指定精度的成功率只有5%，平均迭代次數為263次，對Rosenbrock函數SFLA算法達到指定精度的成功率只有66.67%，平均迭代次數為156次，對Rastrigin函數SFLA算法未能達到指定精度，平均迭代次數為300次。AFSA-SFLA對3個基準測試函數成功率均為100%，并且迭代次數比SFLA迭代次數少很多。

以上仿真結果分析表明，在指定精度下，AFSA-SFLA的成功率、穩定性和計算效率均比SFLA算法有一定優勢。

3.2.3 與他算法尋優結果對比分析 粒子群算法(Particle Swarm Optimization, PSO)的參數設置為速度更新參數C1=1.494 45、C2=1.494 45，種群規模Spop=100，AFSA及AFSA-SFLA的參數設置同3.1小節的參數設置一樣。在d維數為10時對于每一個測試函數均采用AFSA、PSO、AFSA-SFLA各自進展20次試驗，仿真數據如表4所示。

由表4中的仿真數據能看出，對于Griewank函數，AFSA-SFLA的平均尋優結果為0.000 70，PSO的平均尋優結果為0.004 01，AFSA的平均尋優結果為0.083 99，AFSA-SFLA的平均尋優結果是PSO的平均尋優結果的5.74倍，是AFSA的平均尋優結果的119.48倍；對于Rosenbrock函數，AFSA-SFLA的平均尋優結果為3.574 68，PSO的平均尋優結果為9.659 31，AFSA的平均尋優結果為11.326 70，AFSA-SFLA的平均尋優結果是PSO的平均尋優結果的2.70倍，是AFSA的平均尋優結果的3.17倍；對于Rastrigin函數AFSA-SFLA的平均尋優結果為1.03×104，PSO的平均尋優結果為5.912 86，AFSA的平均尋優結果為49.499 70，AFSA-SFLA的平均尋優結果是PSO的平均尋優結果的5.74×104倍，是AFSA的平均尋優結果的4.806×105倍。由此可以看出在維數相同的情況下AFSA-SFLA的尋優精度是最小的，尋優能力是較強的。

4 參數L值對AFSA-SFLA的影響分析

初始化青蛙種群過程中，將AFSA最后一次產生的人工魚群依據適應度值大小降序排序，取占青蛙種群個數的L倍賦值給青蛙種群，作為初始化青蛙種群的一部分，剩余青蛙種群則依照常規的方法進行青蛙的初始化，L為采用人工魚群初始化青蛙的個數占青蛙種群總個數的比例。分析不同比例對AFSA-SFLA所帶來的影響，分別取L為0.3、0.5、0.7時對測試函數進行優化實驗，函數參數設定同3.1節參數設定一樣，其中d為20，每組進行20次實驗，圖8～圖10給出了L值不同的情況下，AFSA-SFLA對測試函數的平均優化結果。

圖8 L取值不同時對Griewank函數的影響

圖9 L取值不同時對Rosenbrock函數的影響

圖10 L取值不同時對Rastrigin函數的影響

由圖8可知，對Griewank函數，L為0.5時，平均尋優優化結果最好，且L為0.3時在迭代40次左右收斂，而L為0.5時在迭代90次左右仍有迭代的趨勢。由圖9可知：對Rosenbrock函數L為0.3時迭代效果最好，且平均尋優結果最好。由圖10可知，對Rastrigin函數L為0.7時平均尋優結果最好，但L為0.5時的迭代效果是較好的。由此可見應根據不同的目標函數選取合適的L值。

5 結 論

為改善SFLA前期收斂速度慢及易陷入局部最優的問題，本文提出了一種人工魚群-蛙跳混合優化算法。算法前期采用ASFA前期搜索速度快的優勢，迅速找到可能的最優解，后期切換至SFLA，初始化青蛙種群時，將ASFA迭代后的結果，取一定比例賦值給青蛙種群，提高了青蛙種群的質量。通過與ASFA、SFLA、PSO 3種算法的比較與分析驗證了混合算法能有效的避免陷入局部最優，且優化精度高。分析混合算法中初始青蛙種群中前期AFSA迭代結果所占的比例對混合算法的影響，結果表明：不同L值對函數的影響不同，故應根據不同的目標函數選擇不同的L值。