PWM頻率對高速無刷直流電動機轉矩脈動影響分析

胡怡婷， 趙朝會， 吉洪智， 丁 帆， 建照陽

(上海電機學院 電氣學院, 上海 201306)

高速無刷直流電動機(Brushless DC Motor, BLDCM)以其小體積、高功率密度、高效率的特點，在眾多領域有廣闊的應用前景[1-3]。BLDCM一般采用相電壓脈沖寬度調制(Pulse Width Modulation, PWM)調速，不同的PWM調制方式對轉矩脈動的影響也有所不同，其中PWM_ON_PWM調制方式具有較小的換相轉矩脈動，且不會造成非導通相電流尾巴問題，因此被廣泛運用[4-5]。

此外，PWM的ON和OFF會造成電流的上下脈動，使得轉矩也產生與PWM同頻率的脈動[6]。為減小這類轉矩脈動，國內外許多學者對此做了眾多研究。文獻[7]通過使用拉普拉斯變換分析電路后改變輸入電壓來減少轉矩脈動問題。文獻[8-9]通過在三相逆變器前加入前級BUCK變換器，完全消除了傳導區的轉矩脈動，但是要加前級電路，較為復雜，成本也增加。文獻[10]指出倍頻PWM控制可以減小電流波動，改善電流波形。文獻[11]通過理論分析并實驗驗證PWM開關頻率不高會導致高速BLDCM滯后換相，引起電流波動。文獻[10-11]都未進一步分析其對轉矩的影響。文獻[12]通過理論和實驗驗證了PWM開關頻率與電磁轉矩成反比關系，并做實驗驗證，但未對15 kHz以上的頻率段進行分析。文獻[13]通過仿真證明了提高PWM的頻率可以有效降低電流脈動和轉矩脈動。

本文采用PWM_ON_PWM調制方式，從PWM頻率入手，分析其與高速BLDCM導通區和換相區轉矩之間的關系。PWM頻率影響電動機的轉矩，隨著PWM頻率的升高，電流斬波更細，電流波動減小，轉矩脈動減小。通過Maxwell和Simplorer軟件搭建單電流閉環的聯合仿真控制模型，仿真驗證了上述結論，并發現當電動機速度在10 000 r/min時，在20 kHz至50 kHz頻率段內，隨著頻率的升高，電動機轉矩脈動抑制效果較為明顯；在50 kHz以上，抑制效果趨于穩定。

1 PWM_ON_PWM調制方式

PWM_ON_PWM調制是新型的調制方式，在開關管導通的120°內前30°和后30° PWM斬波，中間120°常開，如圖1所示。其中，S1～S6為三相橋的開關管。采用此種方法后，電動機轉矩的換相轉矩脈動較小，且避免了非導通相二極管續流的情況[14-15]。

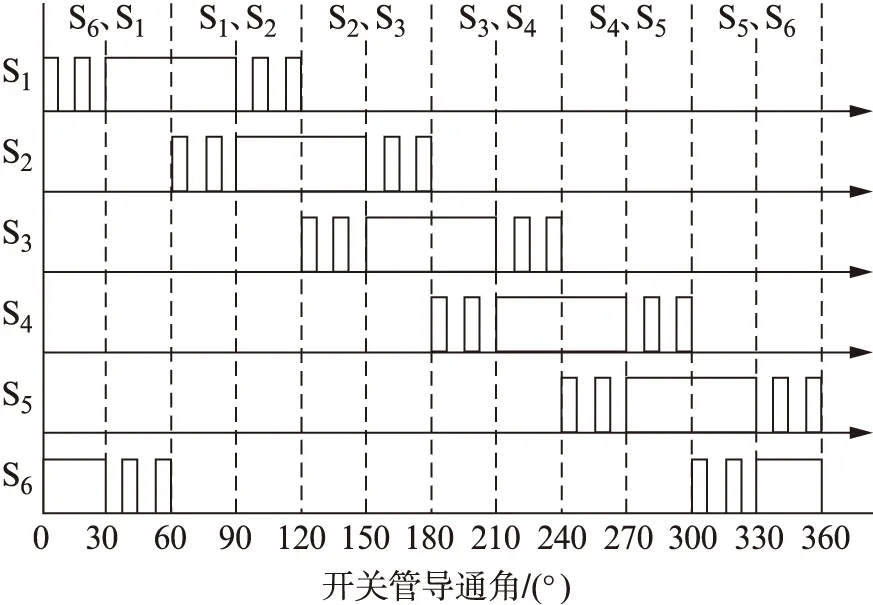
圖1 PWM-ON-PWM

2 PWM頻率對轉矩脈動的影響分析

2.1 BLDCM數學模型

為了便于分析，作出如下假設：三相定子繞組采用Y形連接且對稱分布，各相繞組參數(繞組電阻與電感)大小相同，忽略其變化，磁路不會飽和，忽略電樞反應。

電壓方程為

(1)

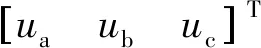
轉矩方程為

(2)

式中：Te為電動機電磁轉矩，N·m；Ω為轉子機械轉速，rad/s。

BLDCM的等效電路如圖2所示。其中UDC為直流電壓；VD1～VD6為反并聯二極管。

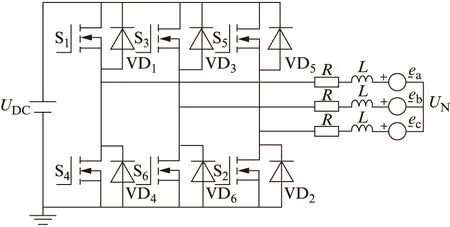
圖2 驅動電路及電動機等效電路

2.2 PWM控制下的電流波動

BLDCM通常采用PWM斬波控制。由于電感的存在，PWM斬波會造成電流出現上下脈動。電動機穩定運行時，當PWM周期很小時，電流波形在PWM=ON或PWM=OFF時可近似為直線，如圖3所示。其中T為PWM周期，D為PWM占空比，I1和I2分別為脈動電流的最小和最大值。

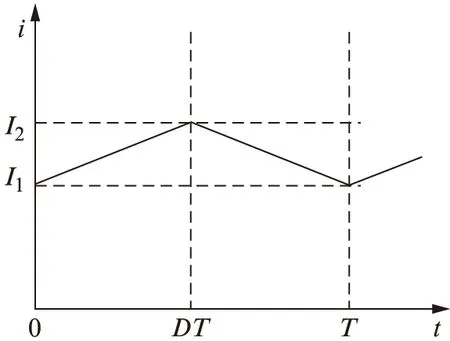
圖3 電感通過的電流波形

因此，電流可分解為一個直流分量和交流分量(三角波)。根據轉矩式(2)可知，轉矩波形也可分解為直流分量和交流分量。

2.3 導通區間轉矩分析

以AB相導通時的0°至30°為例。圖4所示為PWM=ON時的電流流通路徑。

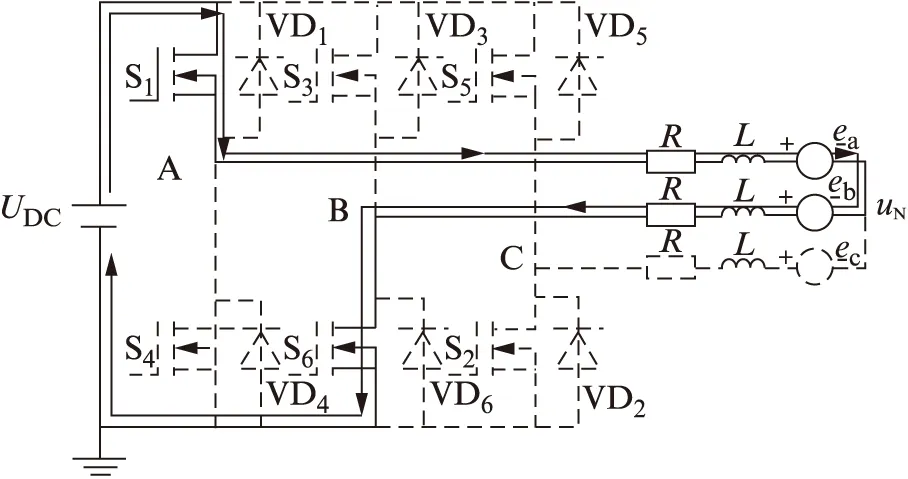
圖4 PWM=ON時的電路

電壓方程為

(3)

式中：I1為電流初值；E為反電動勢的值。

A相電流的變化率為

(4)

A相電流為

(5)

圖5所示為PWM=OFF時的電流流通路徑。

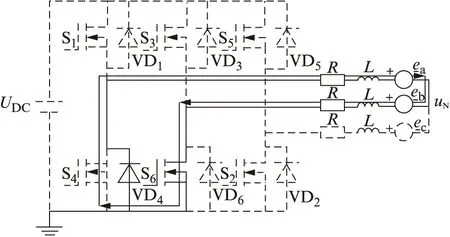
圖5 PWM=OFF時的電路

電壓方程為

(6)

A相電流的變化率為

(7)

A相電流為

(8)

一個開關周期內的電流平均值為

(9)

式中：f為PWM頻率。

電流脈動為

(10)

平均電磁轉矩為

(11)

轉矩波動為

(12)

由式(10)、式(12)可知，當電動機穩定運行時，在一個開關周期內，轉矩脈動和電流脈動表達式一致。轉矩脈動與PWM頻率、UDC、反電動勢以及占空比有關。當UDC、反電動勢以及占空比值一定時，電流脈動及轉矩脈動和PWM頻率成反比關系。開關頻率越高，電流脈動越小，電流品質提高，轉矩脈動越來越小。

2.4 換相區間轉矩分析

當電流從B相換相至C相時，由于電感的存在，流經B相的電流不會立即衰減到0，會通過VD3進行續流。換相開始時，下管S2進行PWM調制，其電路如圖6所示。

電壓方程為

(13)

式中：Is為電流初值。

圖6 PWM=ON時的電路

非換相相電流的變化率為

(14)

非換相相電流為

(15)

當PWM=OFF時其電路如圖7所示。

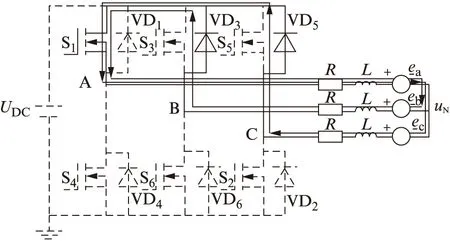
圖7 PWM=OFF時的電路

其電壓方程為

(16)

非換相相電流的變化率為

(17)

非換相相電流為

(18)

一個開關周期內的電流平均值為

(19)

電流脈動為

(20)

平均電磁轉矩為

(21)

轉矩波動為

(22)

由式(20)和式(22)可以看出，換相期間，在一個開關頻率內，電流脈動和轉矩脈動與PWM頻率、UDC、反電動勢以及占空比有關。其中，脈動與PWM頻率成反比關系，隨著PWM頻率的升高，電流脈動和轉矩脈動都會相應減少。

3 仿真分析

在恒轉速10 000 r/min電流PI閉環控制下，采用PWM_ON_PWM調制方式，對不同PWM頻率下電流、轉矩波形進行比較分析。圖8為不同頻率下的電流波形。

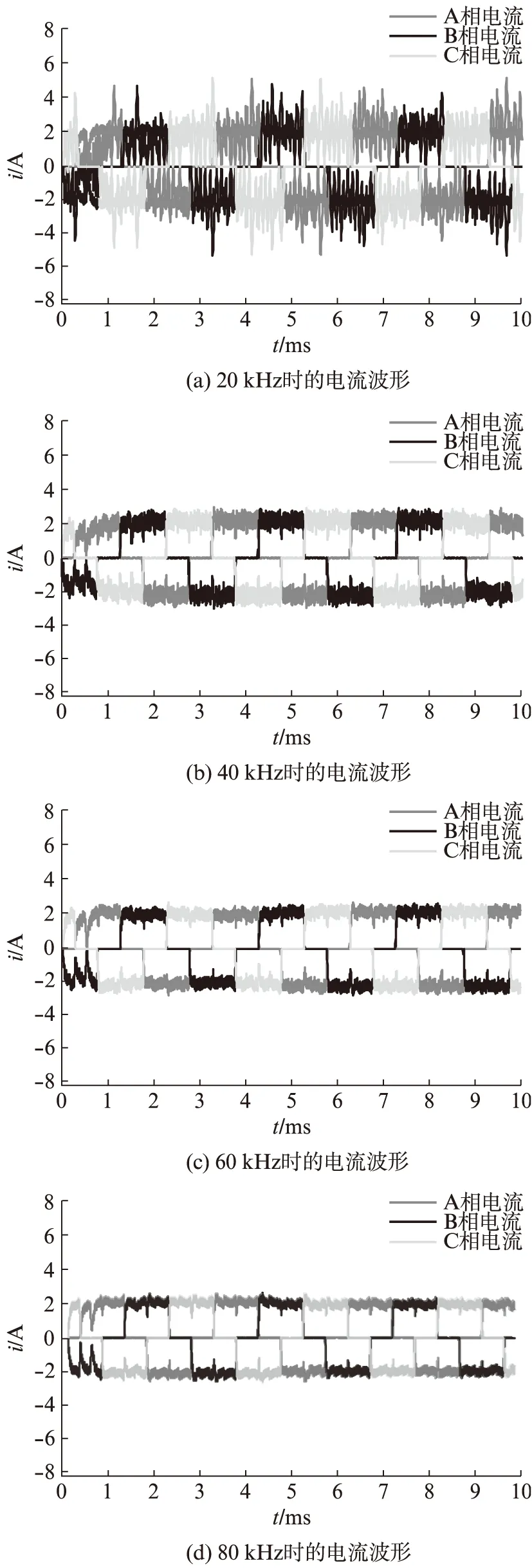
圖8 不同PWM頻率下電流波形

由圖8可知，當PWM頻率為20 kHz，電流脈動很大，也有很多尖峰。隨著PWM增大，電流逐漸趨于平穩，電流尖峰較小，電流品質提高。對于換相期間非換相相電流的跌落問題，當PWM為20 kHz時，非換相相電流最大可跌落至0 A；當PWM為40 kHz時，非換相相電流最大可跌落至1 A左右。對于PWM為60 kHz和80 kHz，兩者非換相相電流最大可跌落的數值差不多。

圖9為不同PWM頻率段下的轉矩波形，當PWM為20 kHz時，最大轉矩達到0.6 N·m，上下脈動幅度很大。當PWM為40 kHz時，轉矩波形明顯好于PWM為20 kHz時候的波形。在非換相期間，轉矩上下脈動幅度在0.1 N·m左右，換相期間轉矩跌落至0.1 N·m左右。當PWM頻率增至60 kHz、80 kHz時，非換相期間轉矩上下波動范圍比低頻時小，但是兩者差距不大。換相期間，這兩個PWM頻率下的轉矩跌落值都差不多。

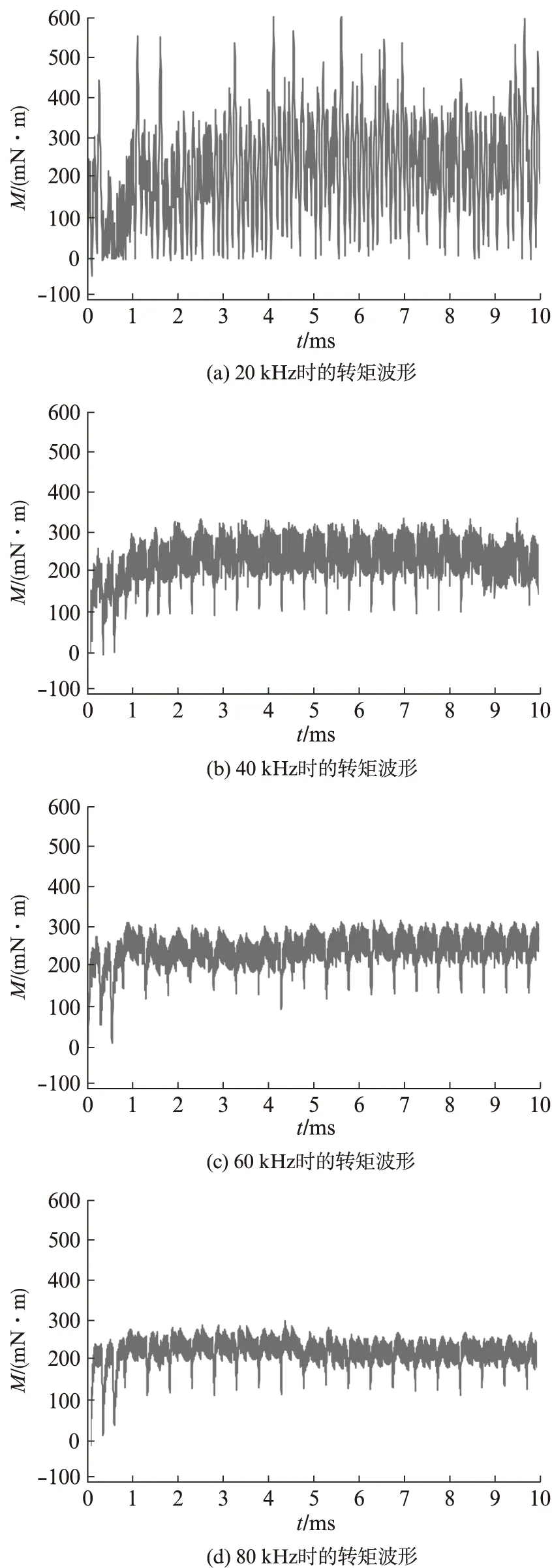
圖9 不同PWM頻率下轉矩波形

為進一步分析PWM頻率對轉矩波動的影響，以10 kHz為間隔，進行不同PWM頻率段仿真。轉矩波形可分解為交流分量和直流分量，對不同PWM頻率下的轉矩波形處理，利用Simplorer中圖形處理功能可計算脈動值。

其公式如下：

(23)

式中：Trip為轉矩脈動值；Tacr為交流分量的有效值；Tm為平均值。轉矩波形可分解為交流分量和直流分量，此公式利用轉矩交流分量有效值與轉矩平均值比值表現轉矩脈動。

表1為軟件算出的脈動值。

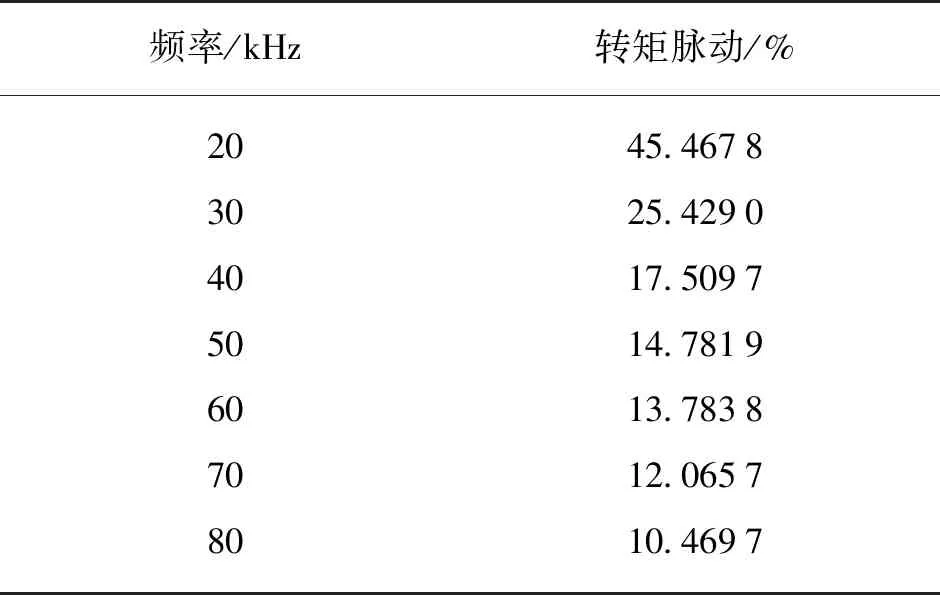
表1 轉矩脈動

由表1可知，隨著開關頻率的增加，轉矩脈動呈減小的趨勢，但是其減小效果是有限度的。在20 kHz到50 kHz頻率段內脈動減小顯著；50 kHz后，脈動值減小趨勢變緩。

4 實驗分析

本文以一臺高速BLDCM作為控制對象，其額定電壓為310 V、額定轉速為24 000 r/min、額定功率為1.2 kW。為實現高頻，采用了基于碳化硅的驅動平臺，主控芯片采用兆易創新的GD32F303。圖10所示為控制平臺。

圖10 實驗平臺

電動機轉速為10 000 r/min，采用PI雙閉環PWM_ON_PWM斬波控制，PWM頻率在10、20、40、60 kHz下的電流波形，如圖11所示。

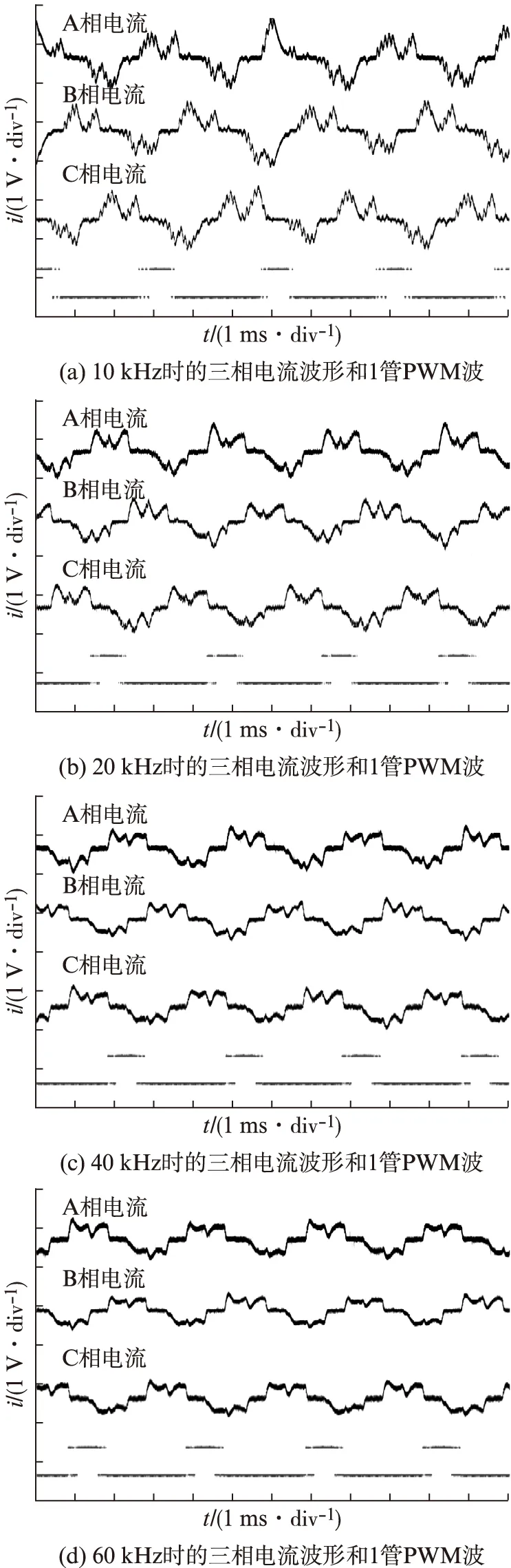
圖11 10 000 r/min下不同PWM頻率電流波形

控制系統中，采用霍爾電流傳感器，其測量出電流值被轉換為電壓值。因此，圖11中顯示的電流波形的單位為電壓單位，電流具體數值需要根據公式進行相關的換算。在10 kHz時電流上下脈動較為明顯，毛刺較多。在20 kHz時電動機毛刺減小，到40 kHz和60 kHz時，基本看不出大的毛刺，變化不明顯。提高PWM頻率可在一定頻率段內顯著減小電流的上下脈動，電流品質提高，從而轉矩脈動減小。當到達某一頻率段后，減小幅度趨于穩定。符合上述理論分析與仿真分析。

4 結 論

本文主要研究了PWM頻率與BLDCM轉矩之間的關系。結合PWM_ON_PWM調制方式，分析了導通期間和換相期間PWM頻率與轉矩間的關系，電動機的轉矩與PWM頻率、直流電壓、反電動勢、占空比有關。PWM頻率和轉矩為反比關系。通過Maxwell、Simplorer進行了仿真驗證，并進行驅動實驗。仿真和實驗均表明：增加PWM頻率，可減小電流上下脈動，從而減少電動機的轉矩脈動，但是其減小效果會在到達某一頻率后趨于穩定。