基于改進(jìn)LuGre摩擦模型的雙旋彈丸固定舵翼滾轉(zhuǎn)位置魯棒自適應(yīng)控制算法

殷婷婷，賈方秀，于紀(jì)言，王曉鳴

(南京理工大學(xué) 智能彈藥技術(shù)國防重點(diǎn)學(xué)科實(shí)驗(yàn)室,江蘇 南京 210094)

0 引言

固定鴨舵式雙旋彈道修正彈具有性價(jià)比高、結(jié)構(gòu)簡單及平臺(tái)適應(yīng)性強(qiáng)等優(yōu)點(diǎn)，已成為當(dāng)前軍事裝備領(lǐng)域的研究熱點(diǎn)[1]。當(dāng)舵翼在隔轉(zhuǎn)摩擦力矩、控制力矩和差動(dòng)舵提供的反向氣動(dòng)力矩作用下到達(dá)指定位置時(shí)，同向舵為彈丸提供側(cè)向操縱力和力矩，實(shí)現(xiàn)二維彈道修正，因此舵翼滾轉(zhuǎn)位置控制是實(shí)現(xiàn)彈道修正的重要研究方向[2-3]。雙旋彈道修正彈具有非線性時(shí)變特性，因此基于該平臺(tái)的舵翼滾轉(zhuǎn)位置控制系統(tǒng)也是一個(gè)非線性系統(tǒng)，主要包含參數(shù)不確定性(如隨溫度及磨損變化的摩擦特性參數(shù)、電氣增益等)和不確定性非線性(如橫風(fēng)等未建模外干擾、非線性摩擦等)，這些模型不確定性成為限制控制性能的重要因素[4]。

為了提高非線性時(shí)變控制系統(tǒng)的跟蹤性能，許多學(xué)者提出了不同的解決方案。為了降低系統(tǒng)參數(shù)不確定性的影響，自適應(yīng)控制器已被廣泛應(yīng)用，但這些控制器無法處理不確定非線性[5]。然而，橫風(fēng)和非線性摩擦等不確定非線性是雙旋彈丸舵翼滾轉(zhuǎn)位置控制中的主要障礙，Alyaqout等[6]提出以魯棒控制器消除上述不確定非線性的影響，但忽略了參數(shù)不確定性的影響。為了同時(shí)處理參數(shù)不確定性和不確定非線性，Yao等[7]提出了一種適用于非線性系統(tǒng)的自適應(yīng)魯棒控制策略，但該方法始終存在控制誤差，容易造成彈道修正偏差；Chang[8]提出了一種自適應(yīng)滑模控制方法，控制誤差趨近于0，但由于存在不連續(xù)函數(shù)，容易造成系統(tǒng)抖振；Patre等[9]提出一種基于誤差符號(hào)的積分魯棒與自適應(yīng)相結(jié)合的控制方法，保證了控制精度和控制輸入的連續(xù)性，但該方法無法處理舵翼滾轉(zhuǎn)系統(tǒng)中的時(shí)變外部擾動(dòng)等不匹配誤差。舵翼滾轉(zhuǎn)系統(tǒng)固有的非線性特性以及各種時(shí)變不確定性，迫切需要設(shè)計(jì)更先進(jìn)可靠的非線性控制策略。

雙旋彈丸舵翼與彈體之間隔轉(zhuǎn)機(jī)構(gòu)的非線性時(shí)變摩擦特性也是影響控制性能的重要因素。前期試驗(yàn)結(jié)果證明，隔轉(zhuǎn)機(jī)構(gòu)摩擦阻尼與鴨舵軸向壓力和相對(duì)滾轉(zhuǎn)速率有關(guān)[10]。為了同時(shí)考慮摩擦中的靜摩擦、庫侖效應(yīng)和動(dòng)態(tài)轉(zhuǎn)速效應(yīng)[11-12]，LuGre摩擦模型得到了廣泛應(yīng)用[13]；然而LuGre模型中的符號(hào)項(xiàng)不連續(xù)，不利于控制器設(shè)計(jì)。Yao等[14]提出以雙曲正切函數(shù)近似不連續(xù)的符號(hào)函數(shù)，保證了摩擦模型的連續(xù)性。建立雙旋通道的連續(xù)可微LuGre摩擦模型，是實(shí)現(xiàn)舵翼滾轉(zhuǎn)位置控制器設(shè)計(jì)和分析的重要環(huán)節(jié)。

基于以上分析，本文針對(duì)舵翼滾轉(zhuǎn)位置控制系統(tǒng)，建立包含連續(xù)可微摩擦模型的系統(tǒng)數(shù)學(xué)模型。基于Lyapunov分析法設(shè)計(jì)了一種將改進(jìn)的連續(xù)LuGre摩擦模型與魯棒自適應(yīng)控制相結(jié)合的控制策略。該控制方法在在線自適應(yīng)估計(jì)系統(tǒng)參數(shù)、摩擦狀態(tài)及外干擾基礎(chǔ)上引入擾動(dòng)補(bǔ)償反饋項(xiàng)，以盡可能降低系統(tǒng)對(duì)參數(shù)不確定性以及時(shí)變擾動(dòng)的敏感度，并通過仿真驗(yàn)證了控制器的有效性。

1 舵翼滾轉(zhuǎn)位置控制系統(tǒng)描述及數(shù)學(xué)模型

舵翼滾轉(zhuǎn)位置控制系統(tǒng)以基于永磁同步發(fā)電機(jī)(PMSG)的雙旋電磁執(zhí)行機(jī)構(gòu)為執(zhí)行器，輸出舵翼滾轉(zhuǎn)控制所需的電磁控制力矩。舵翼在電磁控制力矩Mc、氣動(dòng)力矩Ma和隔轉(zhuǎn)摩擦力矩Md的共同作用下到達(dá)指令位置，如圖1所示。圖1中：fd為系統(tǒng)其他未建模干擾，如模型誤差、外部橫風(fēng)氣流擾動(dòng)和未建模動(dòng)態(tài)等；u為系統(tǒng)控制輸入。

圖1 雙旋彈丸舵翼滾轉(zhuǎn)位置控制系統(tǒng)原理圖Fig.1 Schematic diagram of rudder roll control system in dual-spin projectile

在舵翼滾轉(zhuǎn)位置閉環(huán)控制系統(tǒng)中，系統(tǒng)采用高頻響應(yīng)的電磁執(zhí)行機(jī)構(gòu)，考慮到電氣響應(yīng)速度遠(yuǎn)遠(yuǎn)高于機(jī)械部分，本文建模時(shí)忽略電流環(huán)動(dòng)態(tài)，將電流環(huán)近似簡化為比例環(huán)節(jié)[15]，根據(jù)牛頓第二定律，系統(tǒng)動(dòng)力學(xué)模型為

(1)

式中：J為舵翼轉(zhuǎn)動(dòng)慣量；θf為舵翼滾轉(zhuǎn)位置；Kn為最大電磁控制力矩相對(duì)于轉(zhuǎn)速n的系數(shù)；θp為彈體滾轉(zhuǎn)位置；t為彈丸出炮口的時(shí)間。

(1)式中的氣動(dòng)力矩Ma由舵翼的舵面尺寸、斜置角和滾轉(zhuǎn)狀態(tài)共同決定[16]，如(2)式所示：

(2)

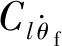
為同時(shí)兼顧摩擦特征和控制器設(shè)計(jì)要求，基于雙旋彈丸隔轉(zhuǎn)機(jī)構(gòu)的滾轉(zhuǎn)特征，以雙旋隔轉(zhuǎn)機(jī)構(gòu)滾轉(zhuǎn)模型代替原模型中的滾轉(zhuǎn)角速度變量，連續(xù)可微LuGre摩擦模型可改寫為

(3)

式中：ωr為雙旋隔轉(zhuǎn)機(jī)構(gòu)滾轉(zhuǎn)角速度；σ0、σ1、σ2為表征摩擦特征的權(quán)重因子；z為模型引入的鬃毛平均變形狀態(tài)量；Fs為靜摩擦力；Fc為庫侖摩擦力，與雙旋彈丸前后級(jí)之間的軸向壓力有關(guān)[16]；a1、a2、a3為表征摩擦特性的形狀系數(shù)。

為了在實(shí)驗(yàn)中優(yōu)化離散的控制器，定義正定函數(shù)N(ωr)=ωr/g(ωr)，則摩擦模型可改寫為如(4)式所示的形式。函數(shù)N(ωr)的正定性可作為后續(xù)控制器穩(wěn)定性證明的依據(jù)，

(4)

(5)

式中：d(t)為未建模擾動(dòng)。

(6)

系統(tǒng)控制器的設(shè)計(jì)目標(biāo)如下：給定系統(tǒng)參考信號(hào)x1d(t)，基于所建立的舵翼滾轉(zhuǎn)系統(tǒng)非線性模型，設(shè)計(jì)一個(gè)有界的控制輸入u，使系統(tǒng)在存在摩擦、非線性以及時(shí)變參數(shù)和擾動(dòng)不確定性問題的情況下，系統(tǒng)的輸出x1盡可能快速準(zhǔn)確地跟蹤x1d(t)。為便于控制器設(shè)計(jì)，作以下假設(shè)：

假設(shè)2定義未知參數(shù)集θ以及不確定非線性項(xiàng)d(t)均有界，即

θ∈{θ:θmin≤θ≤θmax}，|d(t)|≤D，

(7)

式中：θmin和θmax已知，θmin=[θ1min,…,θ6min]T，θmax=[θ1max,…,θ6max]T；D為未知常數(shù)。

2 魯棒自適應(yīng)控制器設(shè)計(jì)

2.1 參數(shù)自適應(yīng)設(shè)計(jì)

2.1.1 模型不確定性參數(shù)集自適應(yīng)率設(shè)計(jì)

由于彈藥發(fā)射條件不完全一致，修正組件也存在個(gè)體差異，基于地面和靶場試驗(yàn)的模型辨識(shí)參數(shù)與實(shí)際值間必然存在偏差，即為控制系統(tǒng)的參數(shù)不確定性。控制器利用實(shí)驗(yàn)得到的模型參數(shù)為初始值，采用在線自適應(yīng)估計(jì)的方法，實(shí)現(xiàn)對(duì)每發(fā)實(shí)驗(yàn)彈丸參數(shù)的準(zhǔn)確估計(jì)。將對(duì)參數(shù)集θ的估計(jì)記作，將估計(jì)誤差記作即定義如下參數(shù)自適應(yīng)不連續(xù)投影映射函數(shù)[17]：

(8)

式中：τi為參數(shù)θi自適應(yīng)函數(shù)，i=1,…,6.

采用以下參數(shù)自適應(yīng)律：

(9)

式中：Γ為正定對(duì)角自適應(yīng)矩陣；τ為參數(shù)集θ的自適應(yīng)函數(shù)，具體形式將在控制器設(shè)計(jì)中給出。不連續(xù)的參數(shù)映射具有如下特性[17]：

∈{:θmin≤≤θmax}，

(10)

(11)

2.1.2 時(shí)變非線性摩擦狀態(tài)量自適應(yīng)率設(shè)計(jì)

摩擦力矩與雙旋轉(zhuǎn)速和軸向風(fēng)阻力相關(guān)，由于氣流擾動(dòng)，軸向風(fēng)阻力具有不可預(yù)測性。除此之外，摩擦力矩受軸承的各向異性、裝配影響嚴(yán)重。因此，摩擦是系統(tǒng)中不確定性非線性問題之一。在LuGre摩擦模型中，狀態(tài)量z為不可測的非線性變量。該狀態(tài)量與狀態(tài)空間方程中的兩項(xiàng)有關(guān)，需要對(duì)兩項(xiàng)中的z值分別進(jìn)行自適應(yīng)估計(jì)，自適應(yīng)律表示[18]為

(12)

(13)

z的上下界可以根據(jù)LuGre摩擦模型推導(dǎo)得出，即zmax=Fs，zmin=-Fs.1和2滿足如下性質(zhì)[18]：

zmin≤j≤zmax，

(14)

(15)

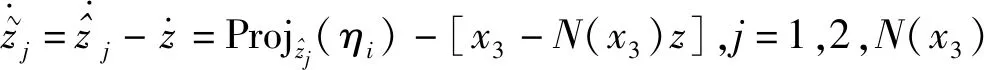
2.1.3 非線性時(shí)變擾動(dòng)上界自適應(yīng)率設(shè)計(jì)

彈丸飛行過程中，氣流不穩(wěn)定造成的舵翼滾轉(zhuǎn)位置抖動(dòng)和未建模的電磁執(zhí)行機(jī)構(gòu)電氣動(dòng)態(tài)特性等均為系統(tǒng)擾動(dòng)因素。由于擾動(dòng)上界是未知狀態(tài)，需要對(duì)擾動(dòng)上界進(jìn)行估計(jì)，自適應(yīng)律可以表示[19]為

(16)

(17)

式中：D的上下界可根據(jù)前期試驗(yàn)數(shù)據(jù)推導(dǎo)得出；滿足如下性質(zhì)[19]：

Dmin≤≤Dmax，

(18)

(19)

2.2 基于改進(jìn)摩擦模型的魯棒自適應(yīng)控制器設(shè)計(jì)

定義舵翼滾轉(zhuǎn)控制系統(tǒng)位置跟蹤誤差e1、輔助誤差量e2以及正定反饋增益k1分別為

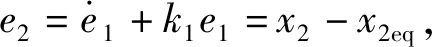
(20)

傳遞函數(shù)H(s)=e1(s)/e2(s)=1/(s+k1)是穩(wěn)定的，即e2與e1同步趨近于0，s為復(fù)變量。基于e1與e2的同步性，系統(tǒng)控制器的設(shè)計(jì)目標(biāo)可由使得輸出x1盡可能快速準(zhǔn)確地跟蹤x1d(t)，轉(zhuǎn)化為使得e2盡可能地小。

結(jié)合(6)式和(20)式，可得

(21)

設(shè)計(jì)魯棒自適應(yīng)控制器u為

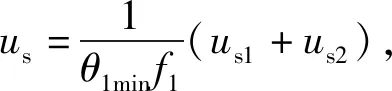
(22)

式中：k2為正定反饋增益；ua為具有在線參數(shù)自適應(yīng)功能的可調(diào)整模型補(bǔ)償項(xiàng)；us1為線性負(fù)定反饋項(xiàng)，用來穩(wěn)定系統(tǒng)的名義模型；us2為用于處理建模不確定性的非線性魯棒反饋項(xiàng)。

將(22)式中的控制參數(shù)u代入動(dòng)態(tài)方程(21)式，可得

(23)

式中：φ[f1ua,f2,f3x2,-1,N(x3)2,-x3]T；設(shè)計(jì)魯棒項(xiàng)

(24)

在呈現(xiàn)所設(shè)計(jì)控制器的主要性能之前，先給出本文中將要用到的控制器參數(shù)的數(shù)學(xué)特性。

2.3 控制器的穩(wěn)定性證明

在給出控制器的穩(wěn)定性證明之前，先確定參數(shù)自適應(yīng)律中的自適應(yīng)函數(shù)τ、η1、η2和ψ如下：

τ=φe2，
η1=x3-N(x3)1-γ1e2，
η2=x3-N(x3)2-γ2N(x3)e2，
ψ=γ3e2，

(25)

式中：γ1、γ2、γ3分別為正定的自適應(yīng)學(xué)習(xí)增益。

選取如下Lyapunov函數(shù)：

(26)

求(26)式函數(shù)V對(duì)時(shí)間微分，并結(jié)合(20)式、(22)式和(24)式，可得

(27)

由θ1≥θ1min、|d(t)|≤D和投影函數(shù)特性，可得

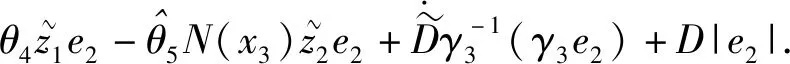
(28)

根據(jù)引理2，可得

(29)

由引理3，可得

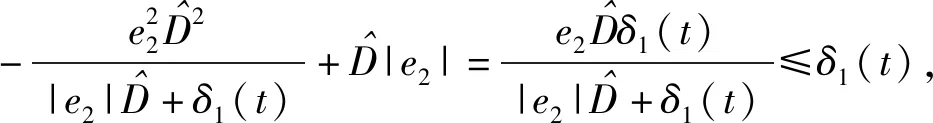
(30)

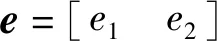
結(jié)合自適應(yīng)函數(shù)τ的特性及θ的投影特性，可得

(31)

根據(jù)LuGre摩擦模型中z的動(dòng)態(tài)特性，可得

(32)

結(jié)合自適應(yīng)函數(shù)η1和η2及z的投影特性可知，

(33)

整理(33)式可得

(34)

將(34)式對(duì)時(shí)間進(jìn)行積分，結(jié)合引理1，可得

(35)

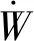
3 仿真實(shí)驗(yàn)結(jié)果及分析

為了驗(yàn)證控制器的有效性，結(jié)合前期實(shí)驗(yàn)數(shù)據(jù)建立舵翼滾轉(zhuǎn)位置控制系統(tǒng)仿真模型。模型以155 mm炮射高旋彈丸外彈道特性為輸入，給定階躍形式的位置指令x1d(t)=1，t>20，對(duì)舵翼滾轉(zhuǎn)位置控制系統(tǒng)進(jìn)行仿真。為了評(píng)估控制器的穩(wěn)態(tài)跟蹤性能，以前期靶場試驗(yàn)數(shù)據(jù)為參考，外部干擾和反饋測量噪聲分別選取幅值為0.03和5×10-4的隨機(jī)噪聲。分別選取以下5種控制器進(jìn)行雙旋彈丸固定鴨舵滾轉(zhuǎn)位置控制的對(duì)比仿真。

1)本文所提基于改進(jìn)LuGre的魯棒自適應(yīng)摩擦補(bǔ)償控制器(RALuGre)。舵翼滾轉(zhuǎn)系統(tǒng)參數(shù)如下：J=2.757×10-4kg·m2，S=0.018 9 m2，d=0.155 0 m，H(0)=0，δ=4°.控制器增益k1=200，k2=15，選定與系統(tǒng)仿真模型存在偏差的參數(shù)作為參數(shù)集自適應(yīng)的初始值：(0)=[0.3,-1×104,4×10-5,1,0,8×10-5]，1(0)=2(0)=0，(0)=0.01;界限：θmax=[1,-1×102,4×10-4,10,10,1×10-4]T，zmax=-zmin=0.1，θmin=[0.1,-1×105,4×10-6,0,-10,1×10-5]T，Dmax=0.1，Dmin=0；對(duì)角自適應(yīng)律矩陣選為Γ=diag{0.01,1,1,1×104,1×102,10}；γ1=γ2=1×10-5，γ3=100.

2)基于摩擦補(bǔ)償?shù)聂敯艨刂破?RLuGre)。在RALuGre控制器的基礎(chǔ)上去除參數(shù)自適應(yīng)，對(duì)比驗(yàn)證參數(shù)自適應(yīng)對(duì)于非線性時(shí)變系統(tǒng)的重要性。

3)基于摩擦補(bǔ)償?shù)淖赃m應(yīng)控制器(ALuGre)。在RALuGre控制器的基礎(chǔ)上去除基于擾動(dòng)估計(jì)的非線性魯棒補(bǔ)償項(xiàng)，對(duì)比驗(yàn)證魯棒補(bǔ)償項(xiàng)的重要性。

4)魯棒自適應(yīng)控制器(RAC)。RAC控制器參數(shù)值與RALuGre參數(shù)值相同，對(duì)比驗(yàn)證連續(xù)可微摩擦模型的可靠性以及摩擦補(bǔ)償?shù)谋匾浴?/p>

5)基于速度前饋補(bǔ)償?shù)谋壤? 積分- 微分(PID)控制器(PIDVF)。將舵翼滾轉(zhuǎn)位置誤差項(xiàng)轉(zhuǎn)化為速度誤差，并基于速度閉環(huán)進(jìn)行前饋補(bǔ)償。

為了評(píng)估控制算法的性能，將控制響應(yīng)時(shí)間Tc、最大跟蹤誤差M、平均跟蹤誤差μ以及跟蹤誤差標(biāo)準(zhǔn)差σ作為性能指標(biāo)，結(jié)果如圖2、圖3和表1所示。

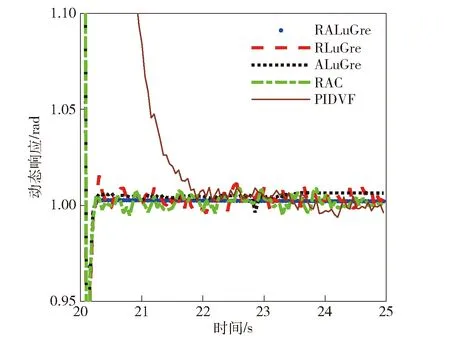
圖2 舵翼滾轉(zhuǎn)位置動(dòng)態(tài)響應(yīng)曲線Fig.2 Response curves of rudder roll position control

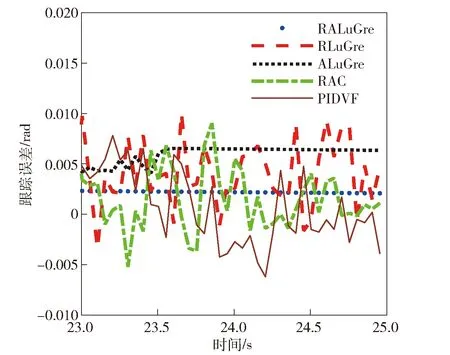
圖3 舵翼滾轉(zhuǎn)位置控制跟蹤誤差曲線Fig.3 Error curves of rudder roll position control

從圖2和圖3中的曲線以及表1中的統(tǒng)計(jì)數(shù)據(jù)可以看出，經(jīng)典PIDVF對(duì)于高度非線性時(shí)變擾動(dòng)系統(tǒng)控制響應(yīng)較為緩慢且跳動(dòng)較大，而RALuGre、RLuGre、ALuGre和RAC均優(yōu)于PIDVF.RALuGre的跟蹤誤差小于RAC，證明了基于改進(jìn)LuGre摩擦模型的參數(shù)估計(jì)和補(bǔ)償方法更精確；RALuGre和RLuGre曲線證明了時(shí)變參數(shù)自適應(yīng)估計(jì)對(duì)于穩(wěn)定控制的必要性；對(duì)比ALuGre和RALuGre可知，在控制器中加入擾動(dòng)補(bǔ)償魯棒性，系統(tǒng)跟蹤誤差可進(jìn)一步減小。

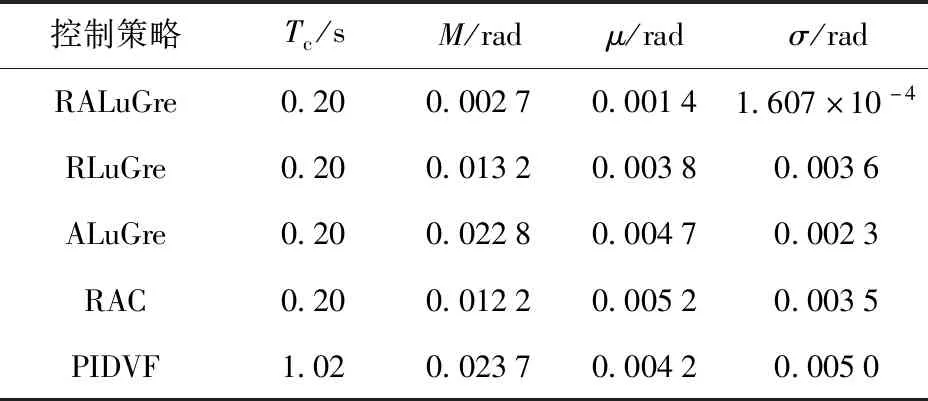
表1 不同控制器的控制性能指標(biāo)參數(shù)Tab.1 Performance indexes of rudder roll position controllers

由5組仿真實(shí)驗(yàn)結(jié)果可知，RALuGre控制器的優(yōu)越性如下：RALuGre控制器采用在線自適應(yīng)方法對(duì)不確定性參數(shù)進(jìn)行估計(jì)，同時(shí)結(jié)合LuGre摩擦模型對(duì)摩擦特征量進(jìn)行估計(jì)，繼而在對(duì)外部擾動(dòng)上界進(jìn)行估計(jì)的基礎(chǔ)上利用魯棒反饋項(xiàng)進(jìn)行補(bǔ)償。

綜上所述，本文仿真結(jié)果驗(yàn)證了所設(shè)計(jì)基于改進(jìn)LuGre摩擦模型魯棒自適應(yīng)控制器的有效性，控制器能夠很快收斂并趨于穩(wěn)定，驗(yàn)證了本文設(shè)計(jì)方法的穩(wěn)定性和可靠性。

4 結(jié)論

本文以基于PMSG為電磁執(zhí)行機(jī)構(gòu)的舵翼滾轉(zhuǎn)位置控制系統(tǒng)為研究對(duì)象，建立了包含改進(jìn)連續(xù)可微LuGre摩擦模型的系統(tǒng)狀態(tài)方程，推導(dǎo)得出了魯棒自適應(yīng)控制器。設(shè)計(jì)自適應(yīng)律估計(jì)不確定性參數(shù)、摩擦特征量以及時(shí)變擾動(dòng)的上界，根據(jù)估計(jì)結(jié)果設(shè)計(jì)魯棒反饋項(xiàng)和模型補(bǔ)償項(xiàng)。最后基于Lyapunov穩(wěn)定性理論證明了系統(tǒng)的全局穩(wěn)定性；通過5種典型控制器的仿真實(shí)驗(yàn)結(jié)果對(duì)比驗(yàn)證了本文所設(shè)計(jì)控制器的有效性和可靠性。得出以下主要結(jié)論：

1)基于魯棒自適應(yīng)控制方法所設(shè)計(jì)的魯棒補(bǔ)償項(xiàng)和模型補(bǔ)償項(xiàng)，能夠有效削弱參數(shù)不確定性和包含摩擦和外部擾動(dòng)的不確定性非線性對(duì)系統(tǒng)控制性能的影響。

2)基于改進(jìn)連續(xù)可微LuGre摩擦模型的魯棒自適應(yīng)控制方法實(shí)現(xiàn)了對(duì)非線性摩擦狀態(tài)量的較好估計(jì)，對(duì)比實(shí)驗(yàn)結(jié)果表明該方法能夠大幅度降低跟蹤誤差的幅值。

本文旨在為雙旋彈道修正彈固定舵翼滾轉(zhuǎn)位置控制系統(tǒng)提供控制策略和方法，考慮到電磁執(zhí)行機(jī)構(gòu)的動(dòng)態(tài)特征會(huì)對(duì)舵翼位置控制系統(tǒng)高頻動(dòng)態(tài)產(chǎn)生影響，后續(xù)將針對(duì)該影響因素開展更深入的研究。