基于反向傳播神經網絡的海雜波參數估計

何耀民，何華鋒，徐永壯，蘇敬，王依繁

(火箭軍工程大學 導彈工程學院，陜西 西安 710025)

0 引言

海雜波是指雷達在海面上形成的散射回波，它受到波浪、海風和潮汐等復雜環境的影響。評估彈載導引頭在不同海況下的打擊精度，迫切需要深入分析海雜波的特性，建立貼近實況下的海雜波模型。目前，關于海雜波的研究和分析主要有基于統計分布和物理特性兩種分析思路。

基于統計分布的方法主要以模型為主，例如對數正態分布、Weibull分布和K分布等。由于K分布模型可以同時考慮海雜波的幅度分布特征和脈沖間相關性能，能夠比其他模型更準確地反映海雜波的統計特性。Conte等[1]、Marier[2]分別利用環不變隨機過程(SIRP)和記憶非線性變換(ZMNL)法對海雜波進行仿真，上述兩種方法是目前使用較廣泛的海雜波仿真方法。Ritchie等[3]通過計算海雜波累積振幅分布得到虛警概率，以此評估海雜波的統計量；Watts[4]和Watts等[5-6]利用多普勒譜記錄的測量結果，分析平均功率譜密度、多普勒譜極值振幅等主要特征，提出一種基于復合K分布的海雜波振幅統計模型，并通過大量海雜波測試數據進行驗證；Weinberg[7-8]利用相互獨立的高斯矢量加權乘積和構造同相正交分量，提出計算更簡單的KK分布海雜波模型。

基于物理性質的方法，通常從海雜波的混沌或分形特性方面進行分析。Haykin等[9]研究分析了實測海雜波的嵌入維數和Lyapunov指數,提出基于混沌相空間重構和反向傳播(BP)神經網絡相結合的小目標檢測算法；隨后，Leung等[10]利用基于相關維數與記憶庫的非線性預測方法進行了目標信號檢測；崔萬照等[11]通過支持向量機(SVM)預測混沌時間序列，實現了目標檢測并得到廣泛推廣。Unswoorth等[12]發現海雜波并非嚴格具備混沌特性；Hu等[13]利用分數布朗運動驗證海雜波具備分形特性，并利用Hurst指數進行海上目標檢測，得到大多學者的認可，成為后續研究熱點[14-16]。國內，行鴻彥等[17-18]利用海雜波的混沌、分形特征，分別提出基于SVM和基于衰減波動分析的多重分形(MF-DFA)目標檢測算法，并不斷加以改進完善；李正周等[19]采用徑向基函數(RBF)神經網絡和空間與時間混沌重構進行小弱目標檢測；劉寧波等[20-21]在頻域分形特性和組合特征上進行了大量分析和研究。

上述文獻單獨從統計分布和物理特性兩個角度分析研究海雜波，均有較大的參考價值。但基于統計分布的海雜波建模并未考慮海雜波物理特性，難以揭示其內在動態特性；基于物理特性的方法，利用存在小目標的海雜波與純海雜波分形參數的差異性，實現海雜波背景下的小目標檢測[17-18]，但未能建立不同海況下的海雜波模型，不便進行仿真評估。另外，目前尚未有相關文獻利用神經網絡挖掘海雜波物理特性和模型參數間的關系。

本文結合統計分布和物理特性兩種分析思路，提出一種基于BP神經網絡的海雜波參數估計法。首先，從海雜波的幅度分布、時間相關性著手，建立基于K分布的時間與空間相關海雜波模型；然后，分析4個模型參數對海雜波混沌特征和分形特征的影響，得出模型參數與物理特性間的定性關系；最后，通過分析海雜波物理特性，利用BP神經網絡反推模型參數，建立貼近實況海雜波的仿真模型，以期為評估彈載導引頭在不同海況下的打擊精度提供模型基礎。

1 基于K分布的海雜波模型

K分布模型[22]由散斑分量(受瑞利分布影響)和調制分量(受伽馬分布影響)組成，該模型可以同時兼顧海雜波的幅度分布特性和脈沖間相關性能，因此是目前使用較廣泛的海雜波模型。

K分布的幅度分布特性和時間相關性可分別由其概率密度函數f(x;v,α)[23]、高斯功率譜密度S(f)[24]表示，如(1)式、(2)式所示：

(1)

式中：x為海雜波的回波幅度；v為形狀參數；α為尺度參數；Γ(v)為伽馬函數；Ku為u階貝塞爾函數。通常v趨于0時有較長拖尾、趨于∞時逼近瑞麗分布。

(2)

式中：σf=2σv/λ為海雜波頻譜均方根，σv為海雜波速度的均方根，λ為雷達波長；fd為平均多普勒頻移。

在綜合分析海雜波幅度分布特征和時間相關性的基礎上，建立基于K分布的時間與空間相關海雜波模型如圖1所示。

圖1 基于K分布的時間與空間相關海雜波模型Fig.1 Spatial-temporal correlation sea clutter model based on K-distribution

傳統方法利用經驗公式、最大似然法或矩估計法估計上述模型參數，雖然可以反映海雜波的統計特性，但未能從其物理意義進行深入分析，難以揭示其內在動態特性。

2 海雜波物理特性分析

由于基于統計方法的參數估計較難反映海雜波的物理特性，本節將從海雜波的混沌特性和分形特性著手，重點分析海雜波主要模型參數對其物理特性的影響，為后續利用BP神經網絡反推模型參數提供理論支撐。

1)海雜波的混沌特性。基于Haykin等[9]對混沌特性的研究，關聯維數D2通常隨著嵌入維數的增加而增大，但在增加到一定程度后將會飽和，即關聯維數可反映海雜波的混沌特性。

2)海雜波的分形特性。對于連續隨機信號X(t)，當滿足(3)式時，稱該信號為自相似信號：

(3)

式中：λ*為比例系數；d表示統計分布相同；H為Hurst指數；t為隨機信號時間。Hu等[13]研究分析得出Hurst指數可較好地表征分形布朗運動特征。

3)海雜波參數仿真。根據第1節中的K分布海雜波模型，分別以形狀參數v、尺度參數α、雜波速度均方根σv、平均多普勒頻移fd為單一變量進行海雜波仿真，再分別通過Grassberger-Procaccia(GP)算法[25]、MF-DFA法[26]求取關聯維數和Hurst指數，4種情況下的仿真參數如表1所示，其關聯維數和Hurst指數的變化如圖2、圖3所示。

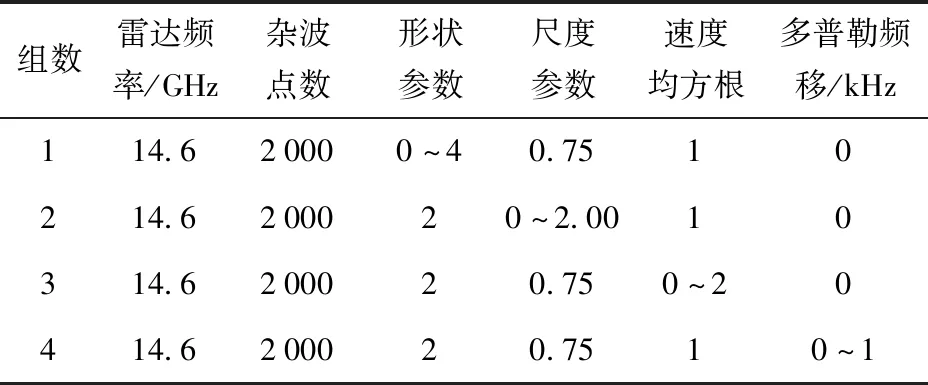
表1 單一模型參數變化對混沌特性的影響Tab.1 Influences of model parameters on chaos characteristics

圖2 不同模型參數對海雜波關聯維數的影響Fig.2 Influences of model parameters on correlation dimension of sea clutter

圖3 不同模型參數對海雜波Hurst指數的影響 Fig.3 Influences of model parameters on sea clutter Hurst index

4)仿真結果分析。觀察圖2(a)、圖2(b)可知，當形狀參數和尺度參數分別在區間[0，4]、[0，2]范圍變化時，關聯維數D2呈整體遞增變化趨勢，表明幅度分布特性的調制分量直接影響海雜波的混沌特性；觀察圖2(c)、圖2(d)可知，對于雜波速度均方根和多普勒頻移，其參數變化對關聯維數D2影響不明顯，即對混沌特性作用不明顯，這種現象與混沌特性主要體現在海浪表面高度變化的物理結構相吻合。

觀察圖3(a)、圖3(c)、圖3(d)可知，當形狀參數、雜波速度均方根和多普勒頻移分別在區間[0，4]、[0，2]、[0，1 000]范圍內變化時，Hurst指數呈整體遞減趨勢，即調制分量和散斑分量均對海雜波的分形特性有直接影響。但觀察圖3(b)可知，當尺度參數變化時，Hurst指數變化無明顯的規律，這是因為利用MF-DFA法[26]求取Hurst指數時，其不完全伽馬函數值的斜率不受尺度參數影響，故Hurst指數無明顯變化規律。

綜上所述，對于基于K分布的海雜波模型，通過仿真形狀參數、尺度參數、雜波速度均方根和多普勒頻移等4個參數的單一變化，可以分析模型參數對關聯維數、Hurst指數的影響作用，其定性關系如表2所示。

表2 模型參數對海雜波的混沌特性及分形特性的影響Tab.2 Influences of model parameters on chaotic and fractal characteristics of sea clutter

3 基于BP神經網絡的參數估計

通過第2節的研究分析可知，模型參數與混沌特性、分形特性之間存在定性關系。基于上述結論，可通過求解二者間的定量關系確定模型參數。與經驗公式、最大似然估計或矩估計法相比，通過混沌特性和分形特性反推模型參數的方法具有較大的實際價值，能大大提高海雜波模型的真實性。但由于模型參數與關聯維數、Hurst指數之間為非線性、高階次對應關系，直接求解存在較大難度，故利用BP神經網絡挖掘數據間的定量關系。

BP神經網絡[27-30]由1個輸入層、若干個隱含層和1個輸出層組成，各層均有1個或多個神經元節點。該模型利用誤差逆傳播算法，通過調整各層連接權值，從而使目標輸入和實際輸出滿足在一定誤差范圍內。

本文參考遺傳算法[31]建立現有BP神經網絡模型，將貝葉斯正則化方法作為模型訓練函數，如(4)式所示：

F=γEw+βEd，

(4)

式中：Ew為整個訓練網絡的權值平方和；Ed為各層網絡誤差值；γ和β為正則化系數。

由于本文中的神經網絡是為了構建4個物理特性與2個模型參數間的定量關系，將多指標即4個物理特性作為神經網絡的輸入、2個模型參數作為輸出。當完成神經網絡的訓練時，確定4個物理特性的大致范圍，通過尋找局部最優的方式反推模型參數。

算法步驟如下：

1)分析真實海雜波的物理特性，得到關聯維數和Hurst指數。

2)利用第1節中的仿真模型生成不同模型參數下的海雜波，作為BP神經網絡的訓練數據。

3)利用訓練數據進行模型訓練，得到神經網絡的連接權值和各神經元閾值。

4)將實況海雜波下的關聯維數和Hurst指數作為已訓練好的神經網絡的輸出，逆向求解海雜波的模型參數。

4 仿真驗證

4.1 實況海雜波的物理特性

本文中的測量數據[32]來自高分辨率Ku波段雷達，信號脈寬為10 μs，距離向分辨率為1.875 m，選取其中連續2 000個數據作為實況海雜波。其概率密度分布曲線、功率譜密度曲線如圖4、圖5所示。

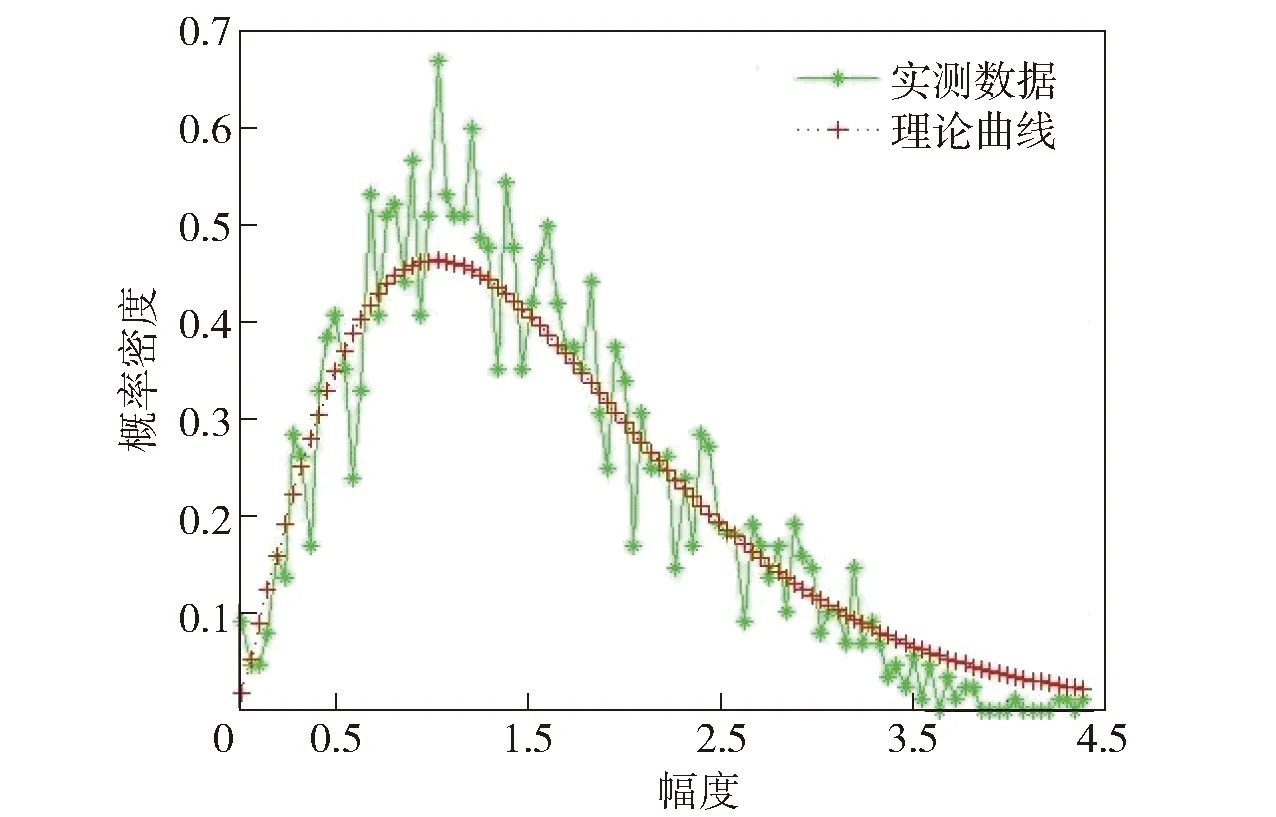
圖4 實況海雜波的概率密度分布曲線Fig.4 Amplitude distribution curves of real sea clutter

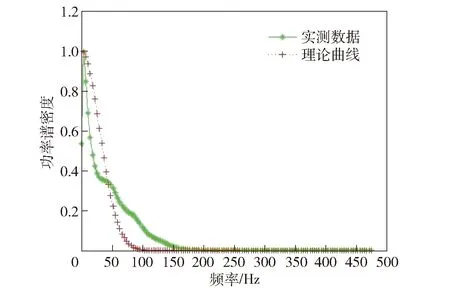
圖5 實況海雜波的功率譜密度曲線Fig.5 Power spectral density curves of real sea clutter

利用GP算法和MF-DFA算法分析海雜波的混沌特性、分形特性：圖6中綠色曲線表示海雜波的關聯維數，當嵌入維數為10時，關聯維數達到飽和，即得到關聯維數D2為2.745；圖7中綠色曲線表示波動函數與序列長度的雙對數關系，海雜波在27～210之間表現出較好的線性關系，如紅色直線所示，其斜率0.081 5為Hurst指數。

圖6 實況海雜波的關聯維數曲線Fig.6 Correlation dimension curve of real sea clutter

圖7 實況海雜波的Hurst指數曲線Fig.7 Hurst exponential curve of real sea clutter

4.2 基于K分布海雜波的訓練數據

利用第1節的海雜波模型，首先通過改變形狀參數、尺度參數、雜波速度均方根、多普勒頻移等4個模型參數，仿真得出32組不同參數下的海雜波；然后利用GP算法、MF-DFA法求解各情況海雜波的關聯維數D2、Hurst指數，結果如表3所示。

表3 K分布海雜波的模型參數對物理特性的影響Tab.3 Influences of model parameters on physical characteristics of sea clutter

4.3 基于BP神經網絡的參數估計

將表3中前28個數據作為訓練樣本、后4個數據作為測試樣本，確定輸入層、輸出層的神經元個數分別為4和1；隱含層數為1、神經元數量為7，學習效率為0.01、訓練次數為1 000、誤差上限為0.000 1.得到連接權值W、閾值S，如表4、表5所示。

表4 輸入、輸出與隱含層神經元的連接權值矩陣WTab.4 Connection weights W of neurons in input and output layers

表5 7個隱含層神經元與2個輸出層神經元的閾值矩陣STab.5 Threshold values S of neurons in hidden and output layers

利用已訓練好的BP神經網絡，分別將歸一化訓練、測試樣本作為輸入，求其預測值；將預測值與實際值進行對比，并用決定系數R2[25]檢驗模型好壞，結果如圖8、表6和表7所示。

圖8 BP神經網絡對海雜波混沌特性的預測Fig.8 Prediction of chaotic characteristics by BP neural network

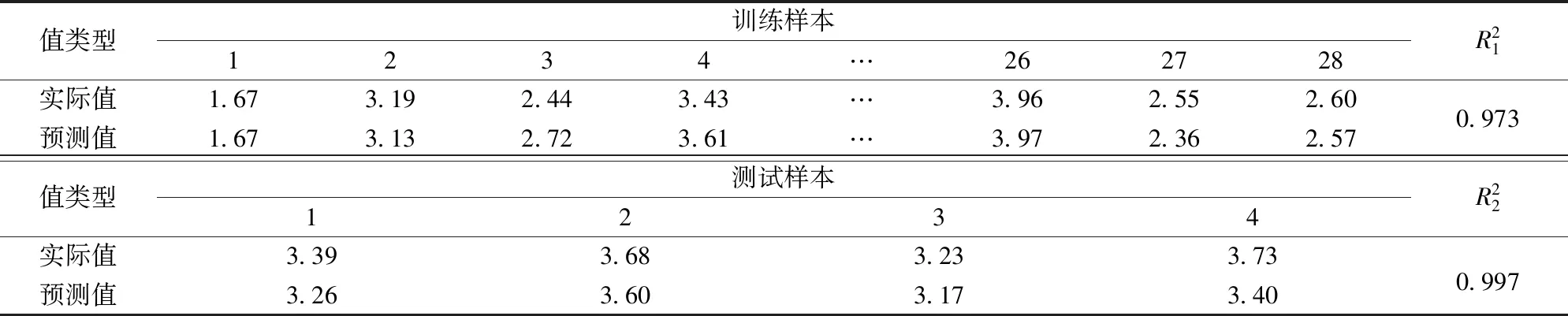
表6 BP神經網絡對關聯維數預測值Tab.6 Prediction of correlation dimension by BP neural network

表7 BP神經網絡對Hurst指數預測值Tab.7 Predicted values of Hurst exponent by BP neural network

觀察圖8可知，由28組訓練樣本生成的神經網絡模型，對訓練樣本(綠色)、測試樣本(紅色)的預測值基本與實際值相吻合，對關聯維數和Hurst指數的平均決定系數為0.985、0.952，從而驗證了該模型能夠有效挖掘模型參數與關聯維數、Hurst指數的定量關系。

通過調整參數比較圖4、圖5中實況海雜波和理論情況下的幅度分布、概率密度函數曲線，確定形狀參數、尺度參數、雜波速度均方差、多普勒頻移的大致范圍為[2.7，3.3]、[0.5，0.6]、[0.6，0.9]、[0，50]；利用表4、表5中的神經網絡完成訓練的BP神經網絡，將4.1節中實況海雜波的Hurst指數、關聯維數作為模型輸出，誤差的上限設定為0.1、0.01，逆向求解海雜波的模型參數，結果如表8所示。

表8 海雜波的模型參數Tab.8 Model parameters of sea clutter

此外，若將模型參數與Hurst指數、關聯維數變換輸入輸出位置，例如將尺度參數、雜波速度均方根、多普勒頻移、關聯維數作為輸入，形狀參數、Hurst指數作為輸出，則導致測試樣本的預測結果并不理想，決定系數低于0.9.上述反例表明模型參數與物理特性間的確存在特定關系，并非利用神經網絡進行隨機的數據處理。

4.4 方法比較

針對4.1節的真實海雜波，利用最大似然估計[33]和矩估計法[34]估計海雜波的形狀參數、尺度參數，而其雜波速度均方根、多普勒頻移通常由經驗公式[24]獲取，參數估計如表9所示。比較3種方法和真實海雜波的概率密度分布特性曲線和概率密度函數曲線，如圖9和圖10所示。

表9 3種參數估計方法對比Tab.9 Comparison of three parameter estimation methods

圖9 不同方法的概率密度分布特性曲線Fig.9 Characteristic curves of amplitude distributions of different methods

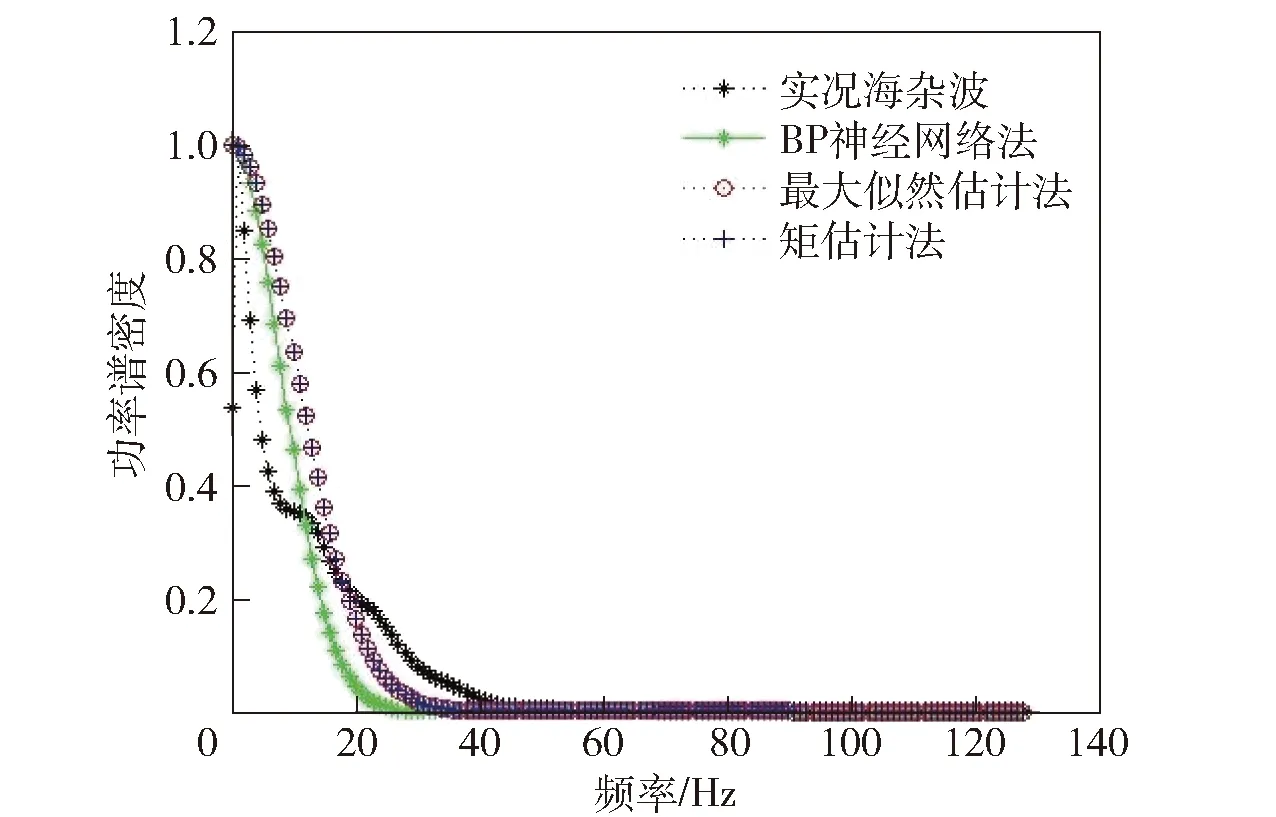
圖10 不同方法的概率密度密度函數曲線Fig.10 Probability density function curves of different methods

由圖9可見，基于BP神經網絡(綠色曲線)和矩估計法(藍色曲線)的幅度分布曲線與實況海雜波(黑色虛線)基本相符，最大似然估計法(紅色曲線)并不理想。由圖10可見，基于BP神經網絡的概率密度函數曲線均優于其他兩種方法。在此基礎上，利用GP算法和MF-DFA法計算各仿真海雜波的關聯維數、Hurst指數，結果如表9所示。

由表9可見，通過最大似然估計法和矩估計法獲得的模型參數，其仿真海雜波的關聯維數、Hurst指數與實況海雜波的差距較大。綜上所述，通過BP神經網絡反推的模型參數，在吻合實況海雜波幅度分布特性、概率密度函數的基礎上，其關聯維數、Hurst指數分別在0.1、0.01的誤差范圍內，能夠較好地體現實況海雜波的物理特性，使海雜波模型更加真實可靠。

5 結論

本文分析了基于SIRP法海雜波模型中的形狀參數、尺度參數、雜波速度均方根和多普勒頻移等4個參數對關聯維數、Hurst指數的影響，提出了基于BP神經網絡的參數估計法。得出主要結論如下：

1)形狀參數在[0，4]區間范圍內對關聯維數、Hurst指數分別起單調遞增和遞減作用，尺度參數在[0，2]區間范圍內，僅對關聯維數起單調遞增作用，雜波速度均方根和多普勒頻移分別在[0，2]區間、[0，1 000]區間范圍內僅對Hurst指數起單調遞減作用，表明了模型參數與物理特性之間的定性關系。

2)利用BP神經網絡可挖掘模型參數與物理特性之間的定量關系，對訓練樣本和測試樣本的決定系數均高于0.95，同時從反例驗證了二者間的確存在某種特定關系。

3)比較本文方法與兩種傳統統計學參數估計的仿真結果，表明本文方法在吻合實況海雜波幅度分布特性、概率密度函數的基礎上，能夠較好地體現實況海雜波的物理特性，為有效評估彈載導引頭在不同海況下的打擊精度提供了模型基礎。