基于改進型入侵野草算法的三軸磁傳感器非正交誤差校正

羅靜博，陳浩，趙苗,翟國君,2

(1.海軍工程大學 兵器工程學院，湖北 武漢 430033；2.海軍海洋測繪研究所，天津 300061)

0 引言

磁場測量是對一個空間矢量場的獲取，若要獲取其完整的信息，采用三軸磁傳感器是一種常用的方式。在現實環境中，由于傳感器加工工藝及安裝水平的限制，傳感器的三軸不可能完全正交，由此會導致三分量磁測誤差[1]。由文獻[2]可知，在45 000 nT地磁背景下，若三軸不正交度為0.25°，則測量誤差就會達到大約100～200 nT，這些誤差會嚴重影響鐵磁性物體的探測，因此對其進行補償是必要的[2-4]。

在已有研究中，文獻[1]提出了一種基于旋轉數據正弦曲線擬合的方法來對三軸磁傳感器非正交誤差進行標定，該方法不需要高精度的磁場參考，但不易獲取平穩的旋轉數據，不利于擬合。文獻[5]提出了以誤差校正矩陣為基礎的快速校正算法，解決了傳統共軛次梯度算法和神經網絡模型的算法復雜的問題。文獻[6]基于總體最小二乘法對捷聯三軸磁力儀的誤差參數進行了估計，相較于傳統最小二乘方法提高了參數估計精度。文獻[7]將三軸傳感器非正交性誤差進行了分離，提出了誤差分離矢量校正法，并結合卡爾曼濾波對校正矩陣參數進行了求解。文獻[8]利用磁數據進行彈體姿態測量，建立了完整形式的地刺傳感器橢球誤差模型，并計算得出誤差校正矩陣參數，但與文獻[1]的局限性一致，不容易得到較好的擬合效果。

本文提出不需要借助高性能磁力儀的最小二乘校正方法，并改進了入侵野草(IWO)算法用以求解該最小二乘校正方法，通過與其他3種智能優化算法的對比，判斷非正交參數標定和數據補償結果的優劣。

1 三軸磁傳感器的非正交誤差模型

圖1 傳感器三軸的非正交關系Fig.1 Non-orthogonal relationship of three-axis magnetic sensor

磁傳感器中，三軸分別為x軸、y軸、z軸，其測量值分別為Bx、By和Bz.取理想正交坐標軸x1、y1和z1，理想的三軸磁數據為Bx1、By1和Bz1.選取兩個坐標系的縱軸z和z1重合，令Oyz和Oy1z1平面重合，其中Oy軸和Oy1軸的夾角為β，Ox1軸與Oxy平面的夾角為γ，x1軸在Oxy平面的投影與x軸的夾角為α，具體對應關系如圖1所示。

由圖1可知，磁傳感器的三軸輸出近似為

(1)

即

B=NB1，

(2)

式中：

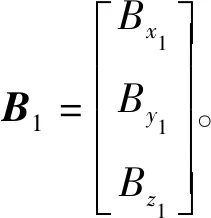
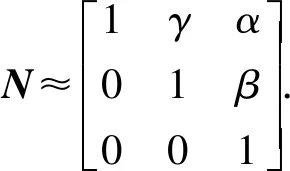
根據(2)式的變換方程得知，傳感器實際測量值與理想正交值存在誤差。設B2為理想正交數據的模值，即

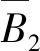
理想三軸正交數據雖然會隨著其與磁場位置的變化而變化，但其模值基本不會變化。利用這一性質，根據最小二乘法，以均方差最小為目標來求解三軸非正交度。建立目標函數如下：

(3)

根據現有的機械工藝水平，假設3個非正交角度在±3°之間，轉換為弧度就是±0.052 36，即

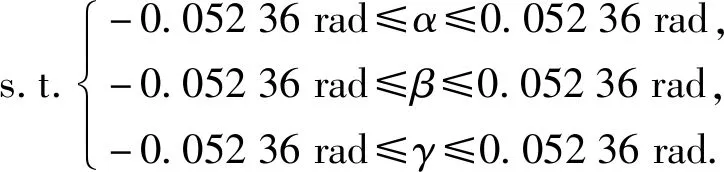
(4)

綜合(3)式和(4)式便構成了三軸磁傳感器的非正交誤差校正的最小二乘方法。最小二乘問題通常通過智能優化算法可以得到較好的解決。

2 基于改進型IWO算法的誤差校正方法

近年來，智能優化算法不斷涌現[9]。IWO算法是2006年由Mehrabian等提出的一種從自然界雜草進化原理演化而來的隨機搜索算法，它具有良好的適應性和收斂性，易于實現[10]。IWO算法是以群體中優秀個體來指導種群的進化，以正態分布動態改變標準差方式，將由優秀個體產生的子代個體疊加在父代個體周圍，再經過個體之間的競爭得到最優個體。IWO算法流程如圖2所示。但由于傳統IWO算法在優化過程中的不可逆性，使得優化結果容易陷入局部最優解，并且其空間擴散范圍較小，使得優化收斂速度較慢。為解決上述問題，對IWO算法進行了改進，在算法的“空間擴散”步驟引入了振蕩因子1+sin (iter)，iter為當前迭代數。

圖2 IWO算法流程圖Fig.2 Flowchart of IWO algorithm

算法具體步驟如下：

1)種群初始化：初始雜草隨機在搜索空間內分布。具體初始化參數確定如表1所示。

2)生長繁殖：適應度高的父代產生的種子多，適應度低的父代產生的種子少。具體新生種子數量由(5)式決定：

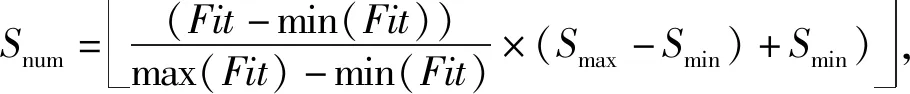
Snum=(Fit-min(Fit))max(Fit)-min(Fit)×(Smax-Smin)+Smin),

(5)

式中：Snum為新生種子數量；Fit表示適應度。

3)空間擴散：子代按照正態分布規則隨機分布在父代周圍；子代正態均值為父代的數值，標準差則隨著迭代次數而改變。變化方式如下：

表1 IWO參數的初始化Tab.1 Initialization of IWO parameters

(6)

式中：SDiter為標準方差的當前值；n為非線性調制參數。

本文改進型IWO算法引入空間擴散的振蕩因子1+sin (iter)，即

(7)

從而有利于在迭代初期更快速地發現較好的解、提升算法收斂性，并在迭代后期擴大搜索范圍，避免陷入局部最優解，有利于尋優精度。

4)競爭淘汰：隨著迭代次數的增加，當種群數超過初始化的最大種群數量后開始淘汰部分個體。淘汰方式是將當前所有個體的適應度排序，淘汰適應度低的個體。

將(4)式描述的參數變量范圍輸入模型參數后，通過上述4個步驟在該范圍內搜尋(3)式描述的最優Fobj，最優值對應的參數變量就是該三軸磁傳感器的三軸非正交度。利用上述最優解可對傳感器進行誤差校正。仿真與實驗結果見第3節和第4節。

為做對比研究，同時利用粒子群優化(PSO)算法、自適應差分進化(DE)算法和禁忌搜索(TS)算法對該最小二乘問題也做了同樣的求解。PSO算法是1995年Kennedy等受鳥類群體行為的啟發而開發的[11]。該算法對非線性、多峰值問題具有良好的全局搜索能力[12-13]。DE算法于1997年由Storn等提出[14]，該算法的關鍵思想是利用種群中隨機選擇的兩個個體來干擾另一個個體[4]，具有較強的魯棒性[15-16]。TS算法最早于1986年由Glover教授提出[17]。該算法在領域搜索的基礎上，通過設置禁忌表來避免已經搜索過的空間的，并通過一些藐視準則來獎勵一些較好的狀態[9]。

3 數值仿真計算分析

設置仿真參數：α=0.2°,β=0.43°,γ=0.36°；地磁場為50 000 nT的標準磁場加-50～50 nT的隨機波動磁場；地磁傾角為47.36°；采樣點為200個，迭代1 000次(為了結果精準)，得到三軸磁場數據，并根據第2節中所述算法進行求解，得到參數結果如表2所示。

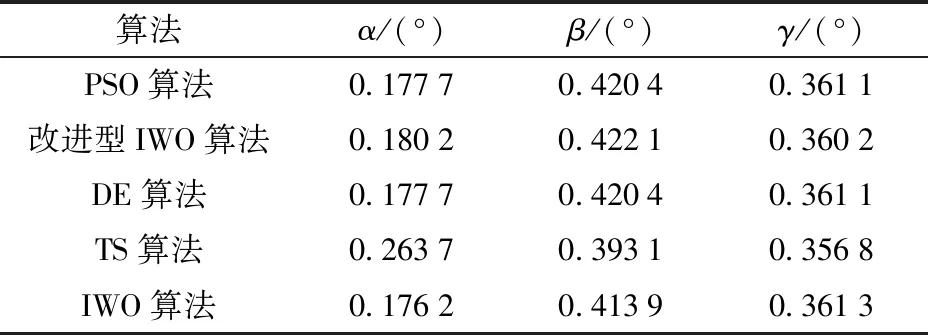
表2 仿真數據的誤差校正參數計算結果Tab.2 Calculated results of error correction parameters of simulation data

由表2可知，采用改進型IWO算法對最小二乘模型求解得到的非正交度參數最接近真實值，3個參數分別收斂于真實值的90.10%、98.16%和100.06%.TS算法結果較差，3個參數分別收斂于真實值的131.85%、96.26%和100.36%.

利用表2的參數計算結果對原始數據進行補償，結果如圖3所示，各算法迭代過程如圖4所示，校正后磁場的波動幅度如表3所示。

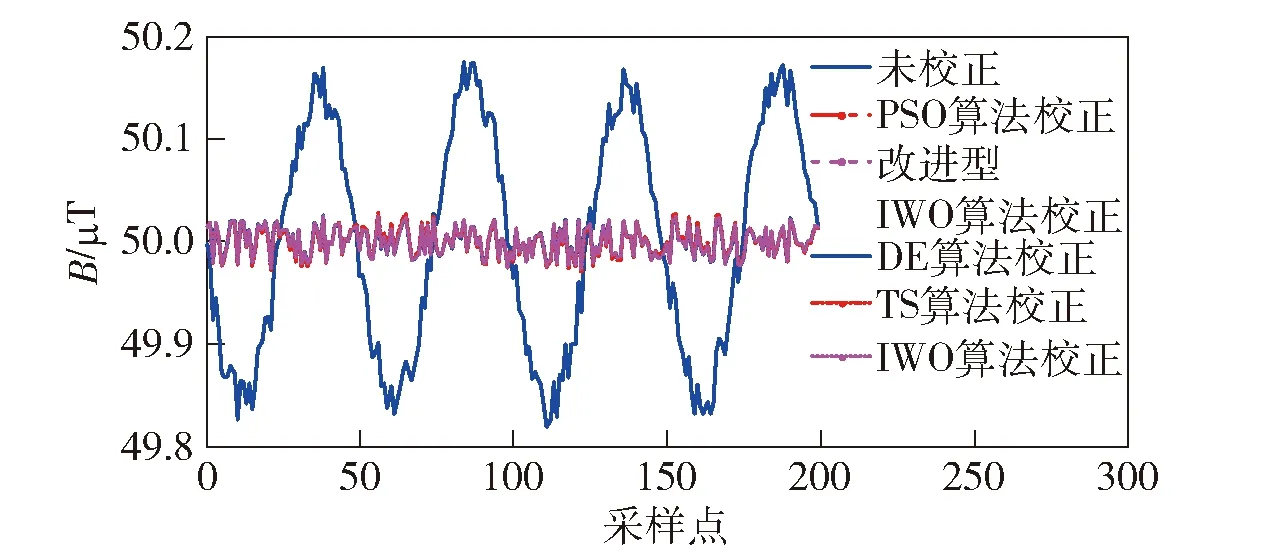
圖3 仿真數據誤差校正的各算法補償結果Fig.3 Compensation results of various algorithms for error correction of simulation data

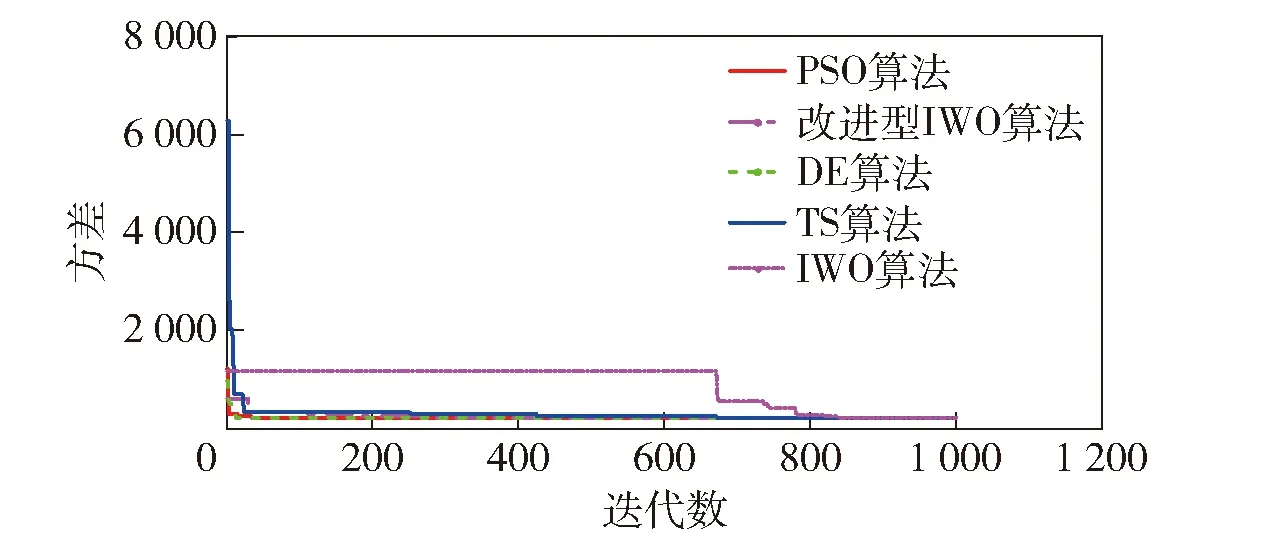
圖4 仿真數據誤差校正的各算法迭代過程Fig.4 Iterative process of each algorithm for error correction of simulation data

由圖4可知，采用改進型IWO算法得到的數據補償結果收斂最快，傳統IWO算法補償收斂速度最慢。由表3可知，采用改進型IWO算法得到的數據補償結果最為穩定，三軸非正交運動噪聲的抑制率為85.42%，符合非正交度模型要求。TS算法補償收斂結果波動相對較大，三軸非正交運動噪聲的抑制率為84.31%.

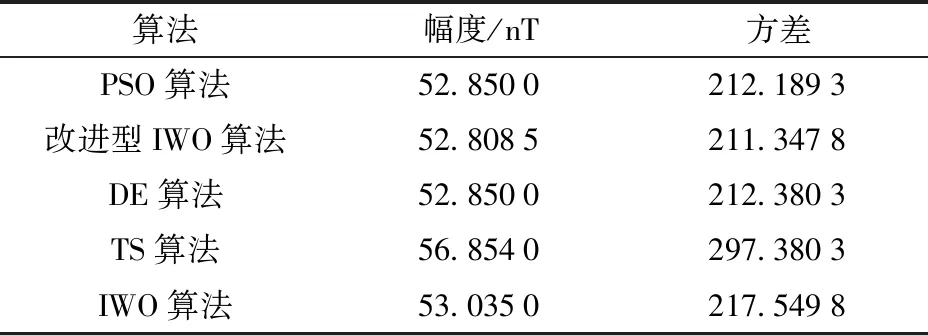
表3 仿真數據誤差校正后磁場波動Tab.3 Magnetic field fluctuation after error correction of simulation data

由于加工工藝的不同，三軸不正交度存在一定偏差。與上述仿真同理，修改α、β和γ的取值(取值在0.1°～1.0°)，繼續做1 000組仿真數據。仿真數據表明：基于改進型IWO算法的三軸非正交誤差校正后，運動噪聲的抑制率為63.157%～96.9%(角度參數取值越大，噪聲越大，抑制率越高)，角度參數都收斂于真實值的87.83%～112.76%.

4 數值實驗計算分析

圖5 三軸磁傳感器Fig.5 Three-axis magnetic sensor

利用美國PNI公司生產的三軸磁傳感器RM3100制作三軸磁場測量裝置(見圖5)，并利用其在三軸合金無磁轉動平臺上進行地磁場的測量，得到三軸磁場數據(見圖6)。對實驗數值求解分析，得到參數結果如表4所示。需要說明的是：本實驗是凌晨在消磁實驗室中進行的，凌晨測量可排除人類活動的磁干擾，消磁實驗室內部物件均不是鐵磁性質的材料，并定期進行磁標定與維護，從而保證了所測得磁場的穩定性。

圖6 三軸合金無磁轉臺實驗測量Fig.6 Experimental measurement of magnetic field on triaxial alloy non-magnetic turntable

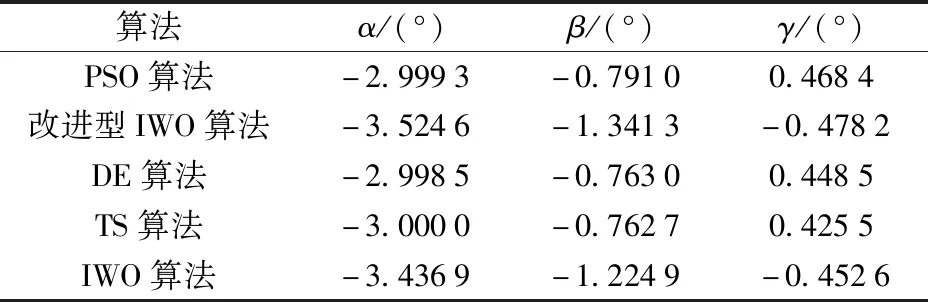
表4 實驗數據的誤差校正參數計算結果Tab.4 Calculated results of error correction parameters of experimental data

利用表4的參數計算結果對原始數據進行補償，結果如圖7所示，各算法迭代過程如圖8所示，校正后磁場的波動幅度如表5所示。

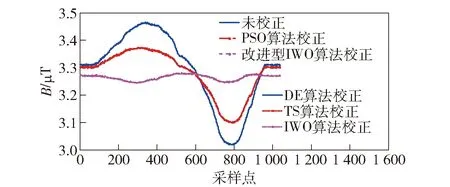
圖7 實驗數據誤差校正的各算法補償結果Fig.7 Compensation results of various algorithms for error correction of experimental data

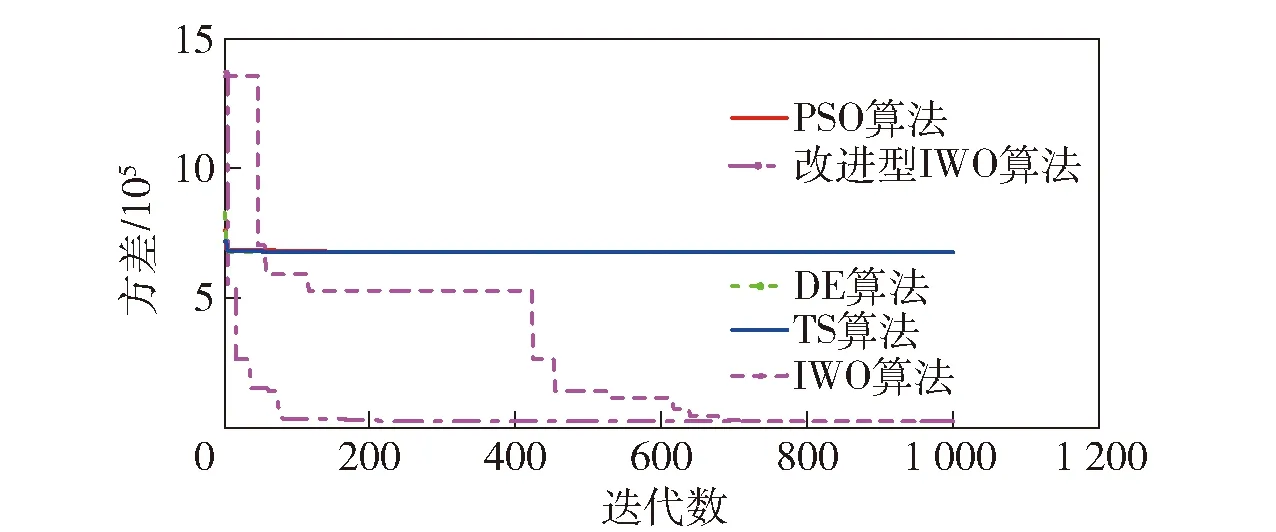
圖8 實驗數據誤差校正的各算法迭代過程Fig.8 Iterative process of each algorithm for error correction of experimental data

表5 實驗數據誤差校正后磁場波動Tab.5 Magnetic field fluctuation after error correction of experimental data

由圖8可知，各算法的收斂速度與仿真結果一致。根據計算結果可知，未校正數據的波動幅度為4.477 2×103nT，采用改進型IWO算法得到的數據補償結果的三軸非正交運動噪聲的抑制率為86.50%，且方差最小。

5 結論

本文通過基于最小二乘的誤差校正方法，實現了三軸磁傳感器的非正交誤差校正與三分量磁數據的補償。得出主要如下結論：

1)基于改進型IWO算法的最小二乘誤差校正方法可以較好地對三軸磁傳感器非正交誤差進行校正。在設定磁場噪聲波動在±50 nT時，仿真結果的3個非正交參數分別收斂于真實值的90.10%、98.16%和100.06%.

2)通過本文方法的校正結果對三分量數據進行補償后，磁場的波動幅度在噪聲范圍內。仿真數據三軸非正交運動噪聲的抑制率大約為85.42%，方差為211.347 8.實驗數據三軸非正交運動噪聲的抑制率大約為86.50%，方差為2.169 6×104.

3)通過本文得到的適用于三軸磁傳感器非正交誤差校正辦法，不需要高精度磁力儀進行參考，簡化了測量設備，并可以補償80%以上的因三軸非正交導致的運動噪聲。