基于多影響因子和重要度的故障樣本優選

邱文昊，連光耀，楊金鵬，黃考利

(1.陸軍工程大學石家莊校區 導彈工程系,河北 石家莊 050003;2.32181部隊,河北 石家莊 050003；3.75833部隊,廣東 廣州 510080)

0 引言

基于故障注入的測試性驗證試驗是評估裝備測試性水平的有效手段[1-2]。開展驗證試驗前，需要從試驗對象的故障模式集中根據樣本量分配結果[3]選取故障樣本；而在相同的合格判據下，不同樣本對應不同的評估結果，因此樣本集結構是否合理，直接影響測試性評估結果的置信度[4]。

目前，關于測試性驗證試驗樣本選取的相關研究較少，具體可以分為兩種方法：一是基于故障率的按比例分層抽樣或簡單隨機抽樣。該方法以故障率為基礎，基于統計理論隨機產生故障樣本。例如美國軍用標準MIL-STD-471A臨時通告2[5]、美國國家技術信息服務局ADA報告[6]、中國國家軍用標準GJB2547A[7]等國內外相關標準，均規定采用隨機抽樣的辦法抽選故障樣本。文獻[8]為降低試驗樣本量，在各功能故障模式中隨機選擇故障樣本進行故障注入；文獻[9]創造性地提出了樣本分配需要滿足符合性和覆蓋性的要求，針對偽隨機抽樣序列偏差大的問題，以故障率抽樣方法為基礎提出了故障樣本準隨機序列抽樣方案；文獻[10]為解決抽樣中故障率數據不準確的問題，研究了故障率計算方法，并以此進行分層抽樣。基于故障率的抽樣存在一定不足，如該方法只是大概率選擇了易發生的故障模式，雖然能夠反映裝備故障發生規律，但忽略了故障率低、一旦發生就會造成較大影響的故障模式[11]，在測試性試驗中，這種情況會對使用方造成較大的試驗風險。二是考慮多因素的綜合抽樣。該方法是在基于故障率抽樣的基礎上，結合測試性試驗要求，綜合考慮裝備使用過程中故障發生后對裝備的影響，使樣本選擇更合理。考慮多因素的抽樣方法在統計理論上與基于故障率的抽樣方法一致，只是增加了表征故障模式屬性的影響因子，能夠更加全面地描述裝備的故障規律，同樣滿足符合性和覆蓋性要求。文獻[12]提出了考慮故障擴散強度的故障樣本抽樣方法，有效提高了試驗樣本集的代表性，但故障模式影響因素仍比較單一，而且故障擴散強度計算過程相對復雜；文獻[13]研究了多影響因素的故障樣本選擇方法，但多影響因素的差異性較大，時間、成本等部分影響因素在工程應用中很難獲得量化值，方法應用比較復雜，可操作性不強。文獻[14]雖然提出了基于故障模式影響及危害性分析(FMECA)的分配方法，在一定程度上解決了信息獲取難的問題，但確定各影響因素權值時主觀性較強，其合理性有待商榷。

測試性驗證是在承制方和使用方共同承擔一定風險情況下的指標評估過程，承制方和使用方對裝備的故障發生規律有不同的認識，雙方關注的故障屬性不同，例如在以故障率為根本的基礎上，承制方更傾向于選擇檢測成本低的樣本，使用方傾向于影響大的樣本。雙方都希望在較小的試驗風險下獲得更合理的試驗結果，因此選擇故障樣本時要兼顧試驗雙方的要求。

本文針對以上分析，提出基于多影響因子和重要度的測試性驗證試驗故障樣本優選方法，通過引入故障傳播強度對FMECA信息進行擴展，確定了故障模式影響因子；在此基礎上提出了權衡相似度和試驗雙方支持度的故障模式重要度模型，并建立了基于相對重要度的故障樣本優選模型。最后，通過與現有方法的對比分析，驗證了本文方法的有效性。

1 故障模式多影響因子確定

1.1 基于擴展FMECA的影響因子分析

定義1故障模式影響因子向量c=(c1,c2,…,cm)，表示能夠表征可更換單元Uw(w=1,2,…,W)故障模式自身屬性的m個影響因子構成的向量，W為可更換單元數量。

定義2故障模式重要度，是指在故障樣本選取中各故障模式重要程度的定量化描述，表達式為

Zi=|c×ω|,i=1,2,…,n，

(1)

式中：ω為影響因子在故障模式重要度評價中的權值向量；n為故障模式數量。

定義3發生度，是指某個故障模式發生的可能性，與故障模式發生概率有關。

定義4嚴酷度，是指某個故障模式對試驗對象的最終影響程度和產生后果的嚴重程度。

定義5檢測度，是指某個故障模式被檢測的可能性，與檢測手段、成本有關。

定義6故障傳播強度，是指某個故障模式發生后對其鄰接故障模式節點的影響程度。

測試性設計的最終目的，是提高裝備的戰備完好性、任務成功性和安全性，減少維修人力和保障資源，降低壽命周期費用。雖然從故障率角度選擇故障樣本更符合裝備故障的發生規律，但是這種抽樣方法只是大概率選擇了易發生的故障模式，無法反映故障模式發生后對裝備的影響，而有些故障模式可能會導致裝備性能完全喪失。故障樣本選擇是檢驗測試性設計水平的關鍵環節，因此從裝備的戰備完好性和任務成功性角度出發選擇試驗樣本時，需要綜合考慮故障發生規律及故障發生后對裝備的影響。

FMECA可以提供多種故障模式屬性信息[15-17]，如故障模式發生度、檢測度、危害度等，可以較好地表征故障模式屬性。但僅由FMECA確定故障模式影響因子還不夠全面，因為FMECA中沒有關于故障模式傳播的定量化信息。裝備實際使用過程中，各組成單元相互關聯耦合、構成一個緊密連接的網絡[18]，故障間的傳播耦合關系非常復雜，一旦發生傳播型故障，將會影響整個系統運行[19]。如果沒有充分對傳播型故障模式進行測試性設計，則將導致使用方風險大大增加。因此，故障樣本選取不能忽略傳播強度大的故障模式對試驗結果的影響。本文在現有FMECA信息的基礎上引入表征故障模式傳播屬性的故障傳播強度作為擴展信息，確定故障模式影響因子，如圖1所示。

圖1 故障模式影響因子Fig.1 Impact factors of failure mode

發生度是由故障率根據等級評定得到的，反映的是裝備的故障發生規律，試驗雙方都希望選擇故障率高的樣本；嚴酷度反映的是故障發生后對裝備的影響，承制方需要重點對該類故障模式進行測試性設計；檢測度反映的是故障模式檢測手段成本的難易高低，承制方進行測試性設計時考慮成本等因素，對較難檢測的故障模式測試性設計不充分，會影響測試性水平；傳播強度反映的是故障模式對其他故障模式或單元的影響程度，若對傳播強度大的故障模式未進行測試性設計，則會對使用方帶來較大風險。因此，選取故障樣本時需要綜合考慮上述影響因子。

1.2 基于改進PageRank算法的故障傳播強度

發生度、嚴酷度和檢測度量值可由FMECA信息提供，下面給出擴展FMECA中傳播強度的求解方法。

求解故障傳播強度不需要詳細分析故障傳播過程，本文提出采用PageRank算法[20]的思想來計算故障傳播強度。故障傳播網絡模型中，故障的傳播對不同節點造成的影響是有差異的，計算故障傳播強度必須考慮各故障模式節點存在的差異，可用風險優先數表示如下:

(2)

定義7鏈入故障模式，是指故障模式網絡模型中所有通過有向邊指向故障模式fmi的故障模式。

定義8鏈出故障模式，是指故障模式網絡中以故障模式fmi為起點、通過有向邊指向的故障模式。

根據故障模式網絡模型，可得故障模式間的鄰接矩陣為A=[aij]n×n，若fmi和fmj有直接關聯關系則aij=1，否則aij=0.傳統的PageRank算法是基于入度評價網頁重要性，而故障是向下傳播的，因此需要構造故障模式轉置鄰接矩陣A′=AT=[a′ij]n×n.

(3)

由于故障模式網絡中存在沒有鏈出故障模式的情況，為防止出現無法收斂的問題，引入衰減系數d[21]，表示故障繼續傳遞的概率，取值為傳播型故障模式與總故障模式的比值，則求解故障模式傳播強度的迭代計算方法為

(4)

2 故障模式相對重要度確定

2.1 基于信息熵的故障模式相似度確定

定義9故障模式相似度，是指故障模式集中各故障模式關于某個影響因子的變化程度。

故障模式相似度越大，各故障模式關于某個影響因子的變化越小，則由該影響因子反映的故障模式差異性就越小。信息熵可以表示數據信息量大小[22]，基于信息熵計算第i個故障模式相似度的過程為

(5)

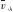
2)故障模式影響因子的信息熵為

(6)

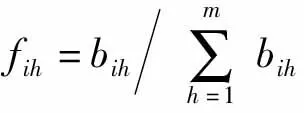
3)故障模式fmi關于第h個影響因子的相似度為

(7)

式中：Eh為第h個影響因子的信息熵；Et為第t個影響因子的信息熵。

2.2 基于相對比較關系的支持度確定

定義10支持度，是指試驗雙方對故障模式各影響因子的重視程度。

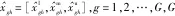
(8)

(9)

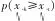
(10)

由相對比較關系的表達式可知，表征相對比較關系可能度構成的矩陣Pm×m=[p(zh≥zt)]m×m為互補判斷矩陣，則承制方對各故障模式影響因子的支持度為

(11)

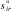
2.3 基于博弈決策的故障模式重要度模型

為獲得合理的故障模式重要度，采用合作博弈的思想，權衡故障模式相似度和雙方支持度在故障模式重要度評價中的相互作用，使三者在綜合決策中達到Nash均衡[26-27]，得到影響因子在故障模式重要度評價中的權值。

(12)

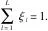
通過博弈論尋找最優的ξl，使得s與各sl的離差極小化，即

(13)

根據矩陣的微分性質，(13)式的最優化導數條件為

(14)

具體地，當L=3時其矩陣形式為

(15)

由(15)式可得ξl，根據(16)式對ξl進行歸一化后，可得權衡系數

(16)

進而得到各影響因子在故障模式重要度評價中的權值向量為

(17)

在各影響因子的最優權值下集結各故障模式影響因子的屬性值，根據(1)式可得故障模式重要度為

(18)

將故障模式重要度由(19)式歸一化后，可得其相對重要度為

(19)

3 基于相對重要度的故障樣本優選模型

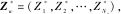
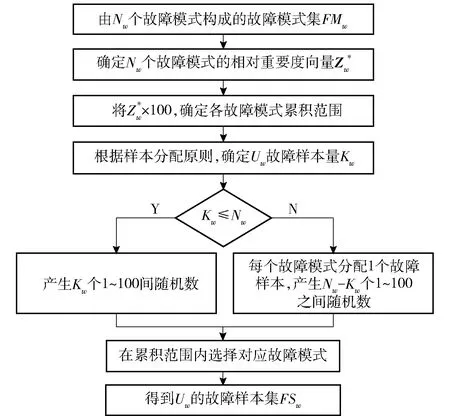
圖2 基于相對重要度模型的故障樣本優選流程Fig.2 Flow chart of failure sample selection based on relative importance

故障樣本優選的具體步驟如下：

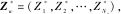
2)將故障模式相對重要度×100，得到各故障模式的累積范圍；

3)若Kw≤Nw，則產生Kw個1～100間的隨機數，記為R′i={r′1,r′2,…,r′Kw}，然后從故障模式集FMw中抽取第r′1,r′2,…,r′Kw個故障模式，構成故障樣本集FSw；

4)若Kw>Nw，則抽取所有故障模式構成集合FFw，然后產生Nw-Kw個1～100間的隨機數，記為i={1,2,…,Nw-Kw}，再從集合FMw中抽取第1,2,…,Nw-Kw個故障模式構成集合FIw，則故障樣本集為FSw=FFw∪FIw.

4 實例驗證

某裝備控制系統由直流電源模塊、主控模塊、通信管理模塊等7個模塊單元組成，主要完成上下級互聯單元的數據傳遞、信息處理和狀態控制等功能。限于篇幅，本文以通信管理模塊為例進行故障樣本優選，由試驗雙方確定的FMECA結果如表1所示。

表1 通信管理模塊FMECATab.1 FMECA of communication management module

圖3 通信管理模塊故障模式網絡結構Fig.3 Failure mode network structure of communication management module

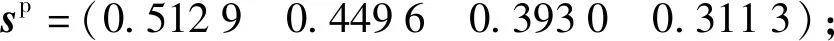
表2 承制方規范化三角模糊數矩陣Tab.2 Normalized triangular fuzzy number matrix of the manufacturer

文獻[14]確定的影響因子為故障率、嚴酷度、平均故障修復時間和危害度，由于本試驗無法獲得平均故障修復時間，影響因子僅包括故障率、嚴酷度和危害度。通過計算可得通信管理模塊各故障模式的影響系數，同時采用本文方法和基于故障率抽樣方法計算各故障模式的抽樣概率，結果如表3所示。

表3 通信管理模塊故障模式抽樣概率Tab.3 Sampling probability of failure modes of communication management module

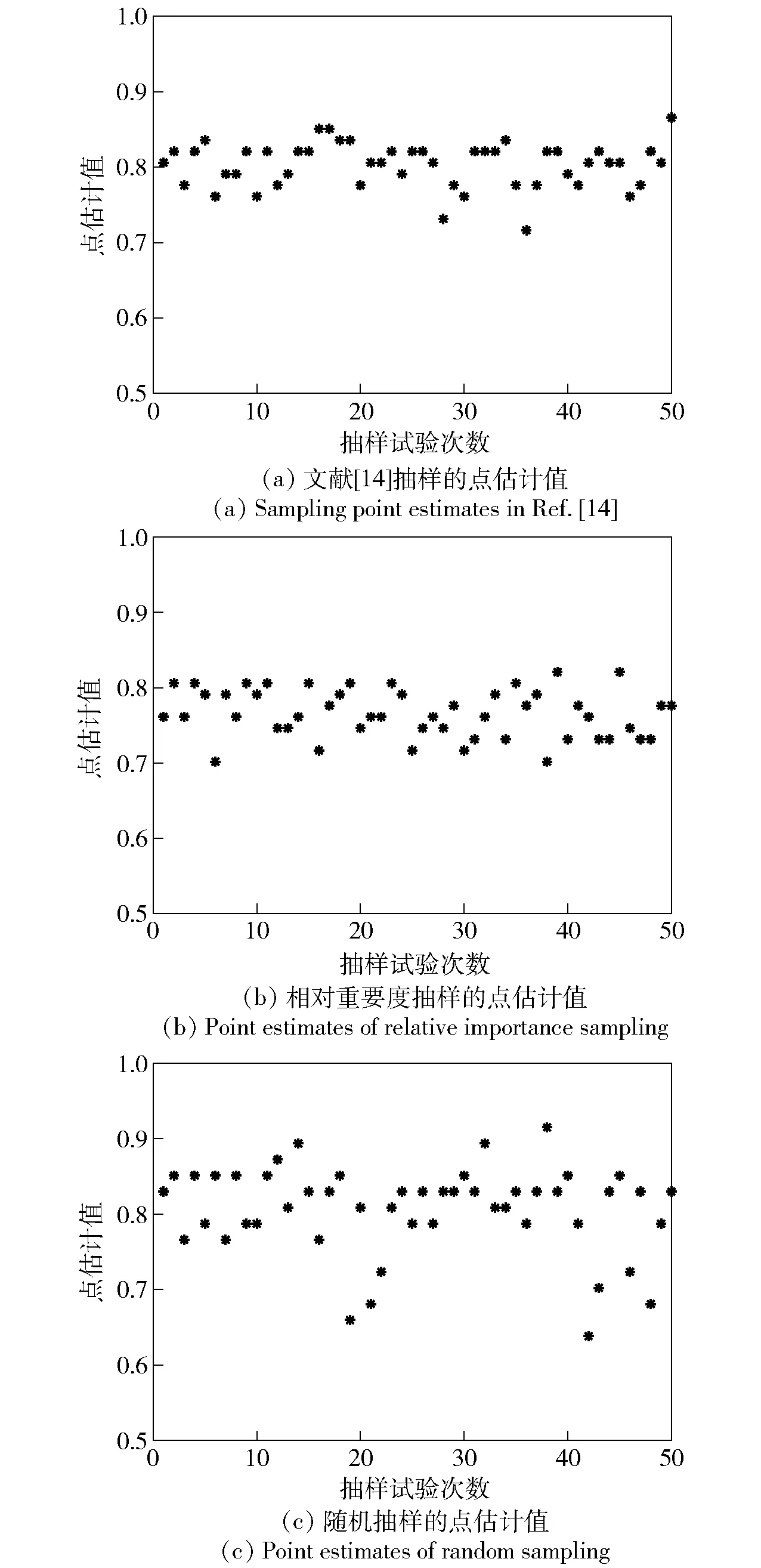
圖4 檢測率點估計值分布Fig.4 Point estimates distribution of detection rate

為分析不同抽樣方法對評估結果的影響，分別采用上述3種方法對控制系統在相同樣本下進行多次模擬抽樣，并計算每次抽樣結果的檢測率點估計值，結果如圖4所示。由上述試驗結果可知：

1)對于故障率抽樣方法，故障率高的故障模式抽樣概率更大(見表3)；而文獻[14]的方法，由于考慮了危害性和嚴酷度，相對于故障率抽樣，增加了故障率高和影響大的故障模式抽樣概率。相對于故障率抽樣法和文獻[14]方法，本文方法增加了故障傳播強度，使得相對重要度大的故障模式更容易被抽到，如fm5故障率相對較低，但嚴酷度和傳播強度較大，如果沒有進行測試性設計，則一旦故障發生將造成較大影響；而且計算影響因子權值時綜合了故障模式相似度和試驗雙方支持度，相比于文獻[14]僅依靠專家經驗確定的權值更客觀合理。因此，本文方法考慮因素更加全面，更能體現測試性驗證試驗需求，而且影響因素數值都可以量化，工程應用性更好。

2)相對于隨機抽樣，相對重要度抽樣和文獻[14]抽樣方法得到的檢測率點估計值分布區間更窄(見圖4)，標準差分別為σ1=0.054 2，σ2=0.032 1，σ3=0.030 0，表明相對重要度抽樣和文獻[14]抽樣方法均能降低單次抽樣引起的評估結果隨機性。文獻[14]抽樣方法多次抽樣得到的指標評估值均值為0.81，相對重要度抽樣為0.76，低于文獻[14]的方法。這是因為對控制系統而言，在同樣考慮故障率的情況下，傳播強度和檢測難度更大的故障模式更容易被抽到，但該部分故障模式檢測率較低，而且文獻[14]方法中的影響因子權值主觀性較強，也導致抽樣不夠合理。因此，本文抽樣方法考慮的影響因子更全面、權值確定更合理，更能全面反映裝備測試性水平。

5 結論

1)基于相對重要度的抽樣方法，綜合考慮了多影響因子和主客觀意義上的影響因子權值，能夠實現測試性驗證試驗中的故障樣本優選。

2)基于相對重要度的抽樣方法可充分利用現有FMECA信息，并引入故障傳播強度，確定故障模式影響因子，全面描述故障發生規律及故障發生后對裝備的影響。

3)基于相對重要度的抽樣方法綜合考慮了故障模式相似度和試驗雙方支持度，采用博弈決策思想權衡各因素在故障模式重要度評價中的相互作用，不僅從客觀數據角度反映權值，還體現了試驗雙方對驗證試驗的影響，相比于主觀賦權值方法，得到的影響因子權值更合理。

4)多次抽樣試驗評估結果表明，從測試性驗證需求角度分析，基于相對重要度的抽樣方法選擇的故障樣本更合理，更能反映裝備測試性水平，樣本選擇滿足符合性、覆蓋性要求；相比于現有多因素抽樣方法，該方法更易獲得影響因子數值，工程應用效果更好。