基于裂紋等效扭轉彈簧模型的裂紋梁振動分析
戴 緣,王天宇,楊 驍
(上海大學土木工程系,上海200444)
由于載荷的作用以及環(huán)境的影響,土木工程和機械工程的中重要構件——梁常常會出現(xiàn)裂紋,導致其承載力降低,使用壽命縮短.因此,研究裂紋梁的動靜力學性能[1-5]及其裂紋的損傷識別對保證梁構件的正常服役具有重要的理論意義和應用背景[6-8].
研究裂紋梁靜力變形和動力響應的一個經(jīng)典方法是將裂紋等效為扭轉彈簧,并以裂紋為界,將裂紋梁分為若干子梁段,各子梁段利用裂紋的等效扭轉彈簧連接,得到裂紋梁的等效分析模型.在此基礎上,每個子梁段利用梁模型進行求解,然后利用梁的邊界條件以及裂紋處等效扭轉彈簧的連續(xù)性條件確定待定系數(shù),從而得到裂紋梁的變形響應[2,9-10].但這種求解方法每增加1條裂紋,其待定系數(shù)就增加4個,導致具體問題的求解較為繁瑣.為此,人們提出利用矩陣傳遞法[7,11-12]以降低求解的復雜性,但是這種方法涉及較復雜的計算,難以給出形式簡單的閉合解析解.
近年來,為簡化分析和計算,基于裂紋的等效扭轉彈簧模型,眾多學者采用廣義Delta函數(shù)刻畫裂紋引起梁剛度的改變,并得到由Heaviside函數(shù)表示的顯式閉合解.Buda等[13]以及Caddemi等[14-15]等采用負Delta函數(shù)刻畫裂紋處梁剛度的變化,然而,該描述在物理上存在欠缺.為此,Palmeri等[1]和Caddemi等[16]采用正Delta函數(shù)描述裂紋處梁彎曲的柔度,從而避免了物理上的非完整性.考慮裂紋縫隙效應以及裂紋的開閉狀態(tài),孫嘉琳等[17]以及Yang等[18]從物理上建立了開閉裂紋梁的等效抗彎剛度,給出了了開閉裂紋梁靜力彎曲的解析閉合解,而汪德江等[19]研究了Timoshenko梁中開閉裂紋位置及裂紋損傷的識別方法.
本工作研究開裂紋Euler-Bernoulli梁的動力特性和動力響應.首先,基于裂紋的等效扭轉彈簧模型,利用Delta函數(shù)給出了裂紋梁的等效抗彎剛度,建立裂紋Euler-Bernoulli梁動力響應的初邊值問題;其次,不同于裂紋梁動力控制方程求解的經(jīng)典變易系數(shù)法[20-21],而是給出了一種較為簡便的通解求解方法,并得到具有任意條裂紋Euler-Bernoulli梁振動模態(tài)的統(tǒng)一顯示表達式.在此基礎上,研究了不同邊界條件下裂紋梁的動力特性,數(shù)值揭示了裂紋深度和數(shù)量等對裂紋梁動力特性的影響.最后,利用模態(tài)疊加法,分析了跨中集中簡諧荷載作用下簡支裂紋梁的動力響應,考察了裂紋深度對裂紋梁動力響應的影響,研究結果對梁裂紋的動力損傷檢測具有一定的指導意義.
1 裂紋梁的自由振動
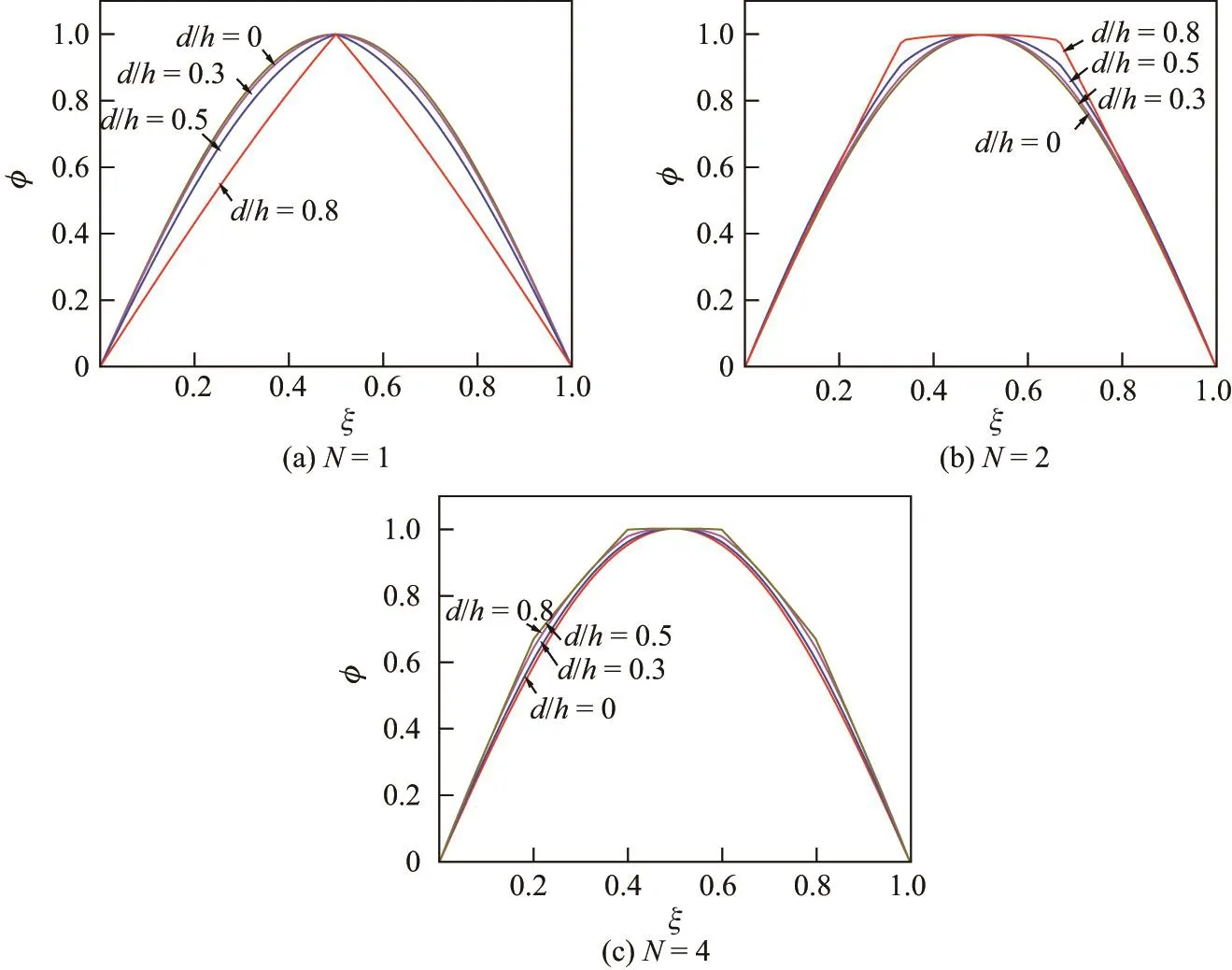
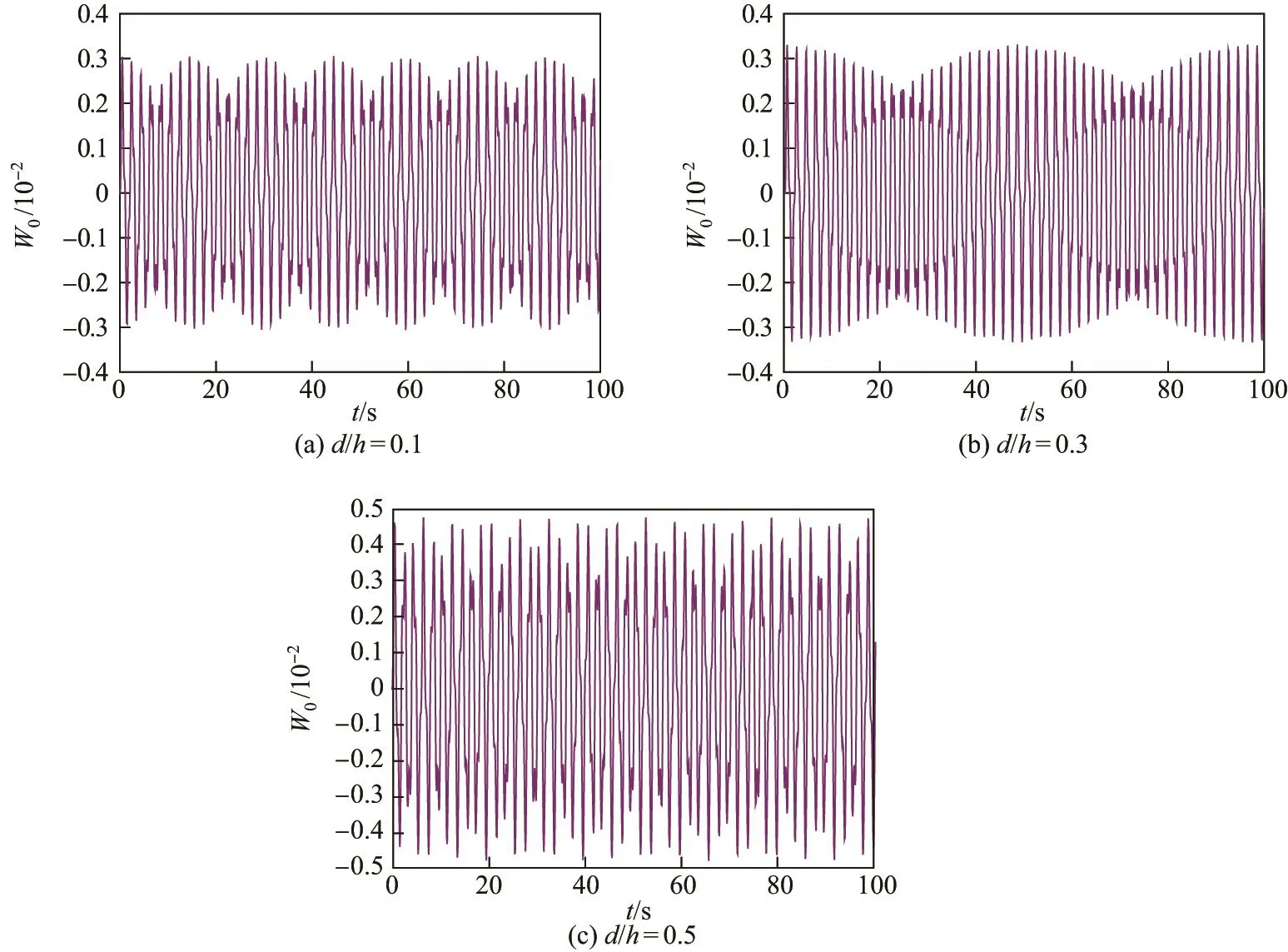
Euler-Bernoulli裂紋梁示意圖如圖1所示.裂紋梁的長和高分別為L和h,抗彎剛度為EI0,在x=xi(i=1,2,···,N)處存在深度為di的開裂紋,且0 式中,δ(x)為廣義Delta函數(shù). 圖 1 Euler-Bernoulli裂紋梁Fig.1 Euler-Bernoulli cracked beam 記裂紋Euler-Bernoulli梁的彎曲撓度為w(x,t),線質(zhì)量密度為m,則其無阻尼自由振動控制方程為 采用材料力學中橫截面上彎矩和剪力的符號規(guī)定[1,13,17],此時裂紋梁任意橫截面彎矩M和剪力FS分別為 對自由振動,利用分離變量法[7,15,21],可得 式中,ω為裂紋梁的自振頻率,α0為相位角,?(x)為對應的模態(tài). 引入如下無量綱量和參數(shù) 可由式(2)推得裂紋Euler-Bernoulli梁無量綱自由振動控制方程 式中,β為由自振頻率ω確定的特征參數(shù),且 由式(4)可得裂紋梁任意橫截面上的無量綱彎矩為 對式(6)兩邊積分2次,可得 式中,D1和D2為待定系數(shù),且 令 則式(9)可表示為 利用Laplace變換及其逆變換,方程式(12)的解可表示為 式中,Ci(i=1,2,3,4)為待定系數(shù). 從而,由式(11)可得 式中, 當裂紋不存在(ki→∞,i=1,2,···,N)時,式(14)退化無裂紋Euler-Bernoulli梁的振動模態(tài),即 由式(14)可求得裂紋梁橫截面上無量綱彎矩的振幅為 由此得 式中, 梁橫截面轉角的振幅為 通常,可利用梁的4個邊界條件,得到待定系數(shù)Ci(i=1,2,3,4)滿足的線性方程 系數(shù)矩陣A的行列式為0,即G(β)=det A(β)=0,給出確定裂紋梁自振頻率的特征方程. 由于裂紋梁的模態(tài)滿足正交性[24-25],在得到裂紋梁自振頻率(i=1,2,···)和模態(tài)(i=1,2,···)后,可運用模態(tài)疊加法進行其動力響應分析.引入裂紋梁的無量綱橫向載荷=q(x,t)L3/(EI)0,則橫向載荷Q(ξ,t)作用下裂紋梁的無阻尼動力控制方程為 式中, 利用初始條件求解方程式(26)可得裂紋梁的動力響應. 考慮具有N條裂紋的簡支梁,且裂紋為等間距分布.由簡支梁的邊界條件可得了φ(0)=0,mb(0)=0,φ(1)=0,mb(1)=0.此時,特征方程式變?yōu)?/p> 求解特征方程式(28)可得簡支裂紋梁的自振頻率,取L/h=20,圖2給出了當裂紋深度相同(di=d,i=1,2,···,N)時,梁中等間距分布不同裂紋數(shù)N的簡支裂紋梁自振頻率參數(shù)β隨無量綱裂紋深度d/h的變化.文獻[22]采用能量法計算了不同裂紋深度下,具有跨中裂紋簡支梁的自振頻率,該簡支梁的幾何及材料參數(shù)如下:梁長L=200 mm,梁截面尺寸b×h為10 mm×10 mm,材料密度ρ=7 850 kg/m3,彈性模量E=200 GPa.以裂紋深度d/h=0.3為例,文獻[22]中裂紋梁的自振頻率為ω0.3=136.290 Hz,代入式(7)第一式,可得β0.3=3.058 3,與采用本工作中的方法所得結果β=3.091 0較為接近,證明了本工作中方法的正確性和有效性.由圖2可以看出,隨著裂紋深度d/h和裂紋數(shù)N的增加,簡支裂紋梁的第一和二自振頻率參數(shù)β減小;當裂紋深度d/h較小時,裂紋深度d/h對自振頻率參數(shù)β的影響較小,而當裂紋深度d/h較大時,裂紋深度d/h對自振頻率參數(shù)β的影響明顯;裂紋數(shù)N對第二自振頻率參數(shù)β的影響較第一自振頻率參數(shù)β的影響更為顯著.當簡支梁只有一條跨中裂紋(N=1)時,第二自振頻率參數(shù)β不依賴于裂紋深度d/h,其原因是此時裂紋梁第二振動模態(tài)為反對稱的,其跨中彎矩為0,裂紋等效扭轉彈簧不發(fā)生作用.因此,裂紋深度對第二自振頻率及其振動模態(tài)無影響. 圖2裂紋數(shù)N不同時簡支裂紋梁自振頻率參數(shù)β隨裂紋深度d/h的變化Fig.2 Variation of frequency parameterβvs.crack depth d/h of the simply-supported cracked beam with different crack number N 圖3 和圖4分別給出了裂紋數(shù)N分別為1,2和4時,不同裂紋深度d/h下簡支裂紋梁第一自振頻率對應的歸一化振動模態(tài)φ及其對應的梁截面轉角.由圖可見,對于簡支裂紋梁,裂紋處歸一化模態(tài)的斜率發(fā)生突變,即歸一化模態(tài)的梁截面轉角發(fā)生跳躍,且隨著裂紋深度d/h增加,歸一化模態(tài)曲線的光滑性減小,在裂紋處斜率突變增加,即歸一化模態(tài)的梁截面轉角跳躍增大. 圖3 不同裂紋數(shù)N和裂紋深度d/h時,簡支裂紋梁的歸一化第一階振動模態(tài)Fig.3 Normalized fundamental vibration mode of the simply-supported cracked beam with different crack number N and crack depth d/h 考慮具有N條裂紋的懸臂梁,且裂紋為等間距分布,此時邊界條件為φ(0)=0,θ(0)=0, 式中, 取L/h=15,圖5給出了當裂紋深度相同,梁中等間距分布不同裂紋數(shù)N時懸臂裂紋梁的第一和第二自振頻率參數(shù)β隨無量綱裂紋深度d/h的變化.由圖可見:隨著裂紋深度d/h和裂紋數(shù)N的增加,懸臂裂紋梁的第一自振頻率參數(shù)β減小;當裂紋深度d/h較小時,裂紋深度d/h對自振頻率參數(shù)β的影響較小;但當裂紋深度d/h較大時,裂紋深度d/h對自振頻率參數(shù)β的影響明顯.同時,具有2條裂紋(N=2)時懸臂梁的第二自振頻率大于具有一條裂紋(N=1)時懸臂梁的第二自振頻率,說明自振頻率不僅受裂紋深度d/h及裂紋數(shù)N的影響,與裂紋位置也有一定關系. 圖4 不同裂紋數(shù)N和裂紋深度d/h時,簡支裂紋梁歸一化第一階振型的梁截面轉角θFig.4 Angleθof beam cross-section of normalized fundamental mode of the simply-supported cracked beam with different crack numbers N and crack depths d/h 圖5不同裂紋數(shù)N時,懸臂裂紋梁自振頻率參數(shù)β隨裂紋深度d/h的變化Fig.5 Variation of frequency parameterβvs.crack depth d/h of the cantilever cracked beam with different crack numbers N 圖6 給出了裂紋數(shù)目N分別為1,2和4,裂紋深度d/h不同時,懸臂裂紋梁第一自振頻率對應的歸一化振型.由圖可見,隨著裂紋深度d/h的增加,振型曲線的光滑性減小,在裂紋處出現(xiàn)斜率突變. 圖6 不同裂紋數(shù)量N和裂紋深度d/h時,懸臂裂紋梁歸一化第一階振動模態(tài)Fig.6 Normalized fundamental vibration mode of the cantilever cracked beam with different crack numbers N and crack depths d/h 考慮具有N條等間距分布裂紋的兩端固支梁,邊界條件為φ(0)=0,θ(0)=0,φ(1)=0,θ(1)=0.此時特征方程式(34)中的系數(shù)為 取L/h=20,圖7給出了裂紋深度相同(di=d,i=1,2,···,N)時,梁中等間距分布不同裂紋數(shù)N的兩端固支裂紋梁第一和第二自振頻率參數(shù)β隨無量綱裂紋深度d/h的變化.文獻[23]采用Rayleigh-Ritz法計算了不同裂紋深度下,具有跨中裂紋簡支梁的自振頻率.簡支梁的幾何及材料參數(shù)如下:梁長L=200 mm,梁截面尺b×h為20 mm×10 mm,材料密度ρ=7 850 kg/m3,彈性模量E=200 GPa,以裂紋深度d/h=0.3為例,文獻[23]中裂紋梁的自振頻率為ω0.3=449.588 Hz,代入式(7)第一式,可得β0.3=4.671,而本工作所得結果β=4.696.隨著裂紋深度d/h和裂紋數(shù)N的增加,固支裂紋梁的第一自振頻率參數(shù)β減小;當裂紋深度d/h較小時,裂紋深度d/h對自振頻率參數(shù)β的影響較小;但當裂紋深度d/h較大時,裂紋深度d/h對自振頻率參數(shù)β的影響明顯.自振頻率不僅受裂紋深度d/h及裂紋數(shù)目N的影響,與裂紋位置也有一定關系.當裂紋深度較深時,裂紋梁的第一第二自振頻率與裂紋深度關系的曲線都出現(xiàn)了交叉,此時裂紋位置對兩端固支梁的頻率影響較大.當兩固支端梁只有一條跨中裂紋(N=1)時,第二自振頻率參數(shù)β不依賴于裂紋深度d/h,此時,跨中彎矩為0,裂紋等效扭轉彈簧不發(fā)生作用 圖7 裂紋數(shù)N不同時兩端固支裂紋梁自振頻率參數(shù)β隨裂紋深度d/h的變化Fig.7 Variation of frequency parameterβvs.crack depth d/h of the clamped-clamped cracked beam with different crack numbers N 作為裂紋梁動力響應分析模態(tài)疊加法的一個簡單應用,考慮初始未變形,具有N條等間距裂紋的簡支梁在跨中集中簡諧載荷作用下的動力響應.此時,有Q(ξ,t)=Fδ(ξ?0.5)sinωt,在初始條件下,方程式(31)的解為 圖8 簡諧集中荷載作用下簡支裂紋梁跨中撓度W0的動力響應Fig.8 Dynamic response of mid-span deflection W0 of simply-supported cracked beam under harmonic concentrated load 取簡支梁梁長L=300 mm,梁截面尺b×h為20 mm×20 mm,所用材料的密度ρ=7 850 kg/m3,彈性模量E=200 GPa,外部激勵的圓頻率ω=230.1 Hz,F=0.33 kN.圖9給出了簡支梁跨中裂紋不同深度d/h時,無量綱跨中撓度W0(t)=W(0.5,t)隨時間t的響應.可見,隨著裂紋深度的增加d/h,無量綱跨中撓度W0(t)振幅增加,其原因是裂紋深度的增加導致梁整體剛度的減少,從而梁的變形增大,并且,隨著裂紋深度的增加,振幅變化加劇. 本工作研究了開裂紋Euler-Bernoulli梁動力特性和動力響應的計算方法.在給出裂紋梁等效抗彎剛度的基礎上,為避免變易系數(shù)法的復雜運算,建立了一種新的裂紋梁動力控制方程通解,即裂紋梁自由振動的求解方法.數(shù)值分析了簡支、懸臂和兩端固支裂紋梁的自振頻率和振動模態(tài),考察了裂紋數(shù)量和深度等對裂紋梁自振頻率的影響;同時,利用模態(tài)疊加法計算分析了簡支裂紋梁在集中簡諧載荷作用下的動力響應,得到了如下結論. (1)基于開裂紋的等效彈簧模型,可以得到具有任意條裂紋的Euler-Bernoulli梁自由振動模態(tài)的統(tǒng)一顯式表達式,該表達式自動滿足裂紋處梁的連續(xù)性調(diào)節(jié),避免了經(jīng)典方法中連續(xù)性條件導致的繁雜求解過程,并且自由振動通解的求解方法避免了采用變易系數(shù)法求解的復雜運算. (2)隨著裂紋深度和裂紋條數(shù)的增加,裂紋梁的自振頻率減小;隨著裂紋深度的增加,裂紋對自振頻率的影響更為顯著.同時,裂紋條數(shù)N對第二自振頻率的影響較對第一自振頻率的影響顯著. (3)裂紋梁的模態(tài)曲線在裂紋處出現(xiàn)尖點,其斜率發(fā)生突變;隨著裂紋深度增加,裂紋處斜率突變增加. (4)裂紋對裂紋梁模態(tài)和頻率的影響依賴于裂紋位置,當裂紋處的彎矩為0時,裂紋對梁振動模態(tài)和頻率沒有影響. (5)由于裂紋梁模態(tài)滿足正交性,因此,可采用模態(tài)疊加法分析裂紋梁的動力響應.對于具有一條跨中裂紋的簡支梁,跨中集中簡諧載荷作用下梁跨中撓度振幅隨裂紋深度的增加而增加,且其振幅變化加劇.



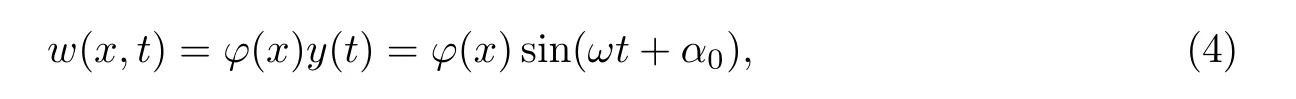



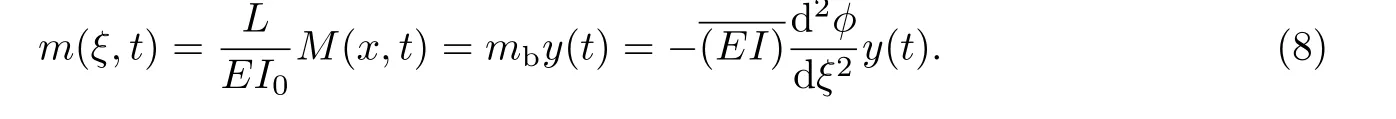

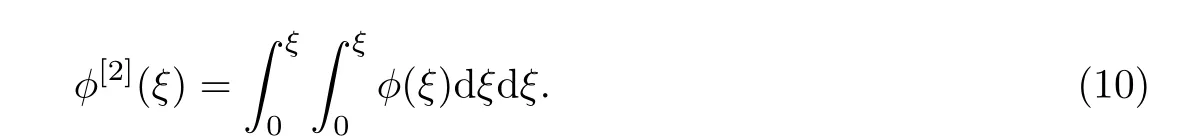
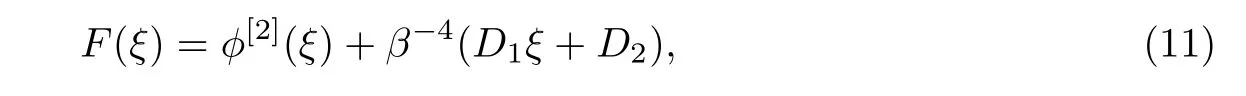
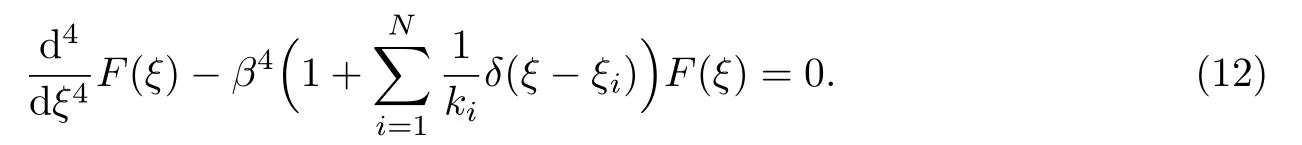
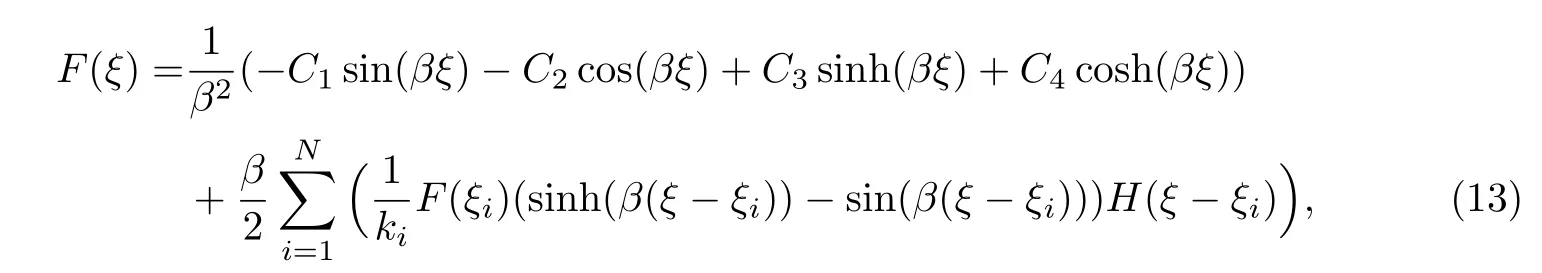
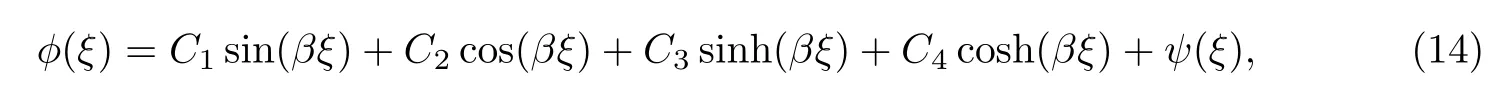





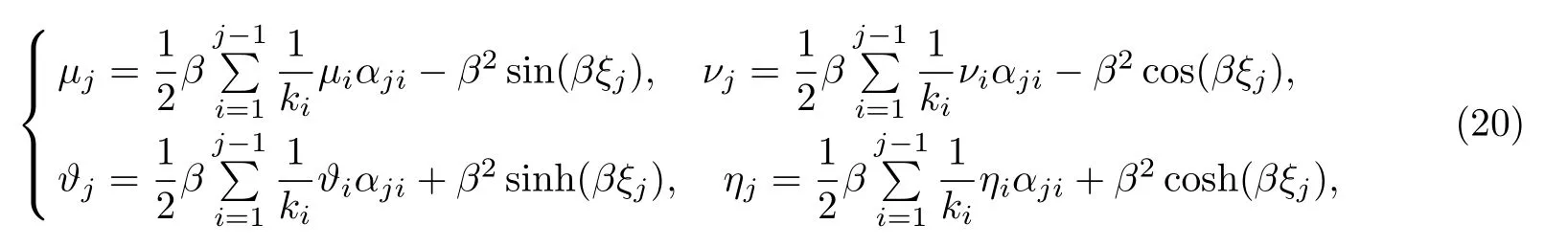


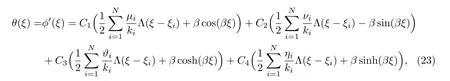

2 裂紋梁的動力響應分析
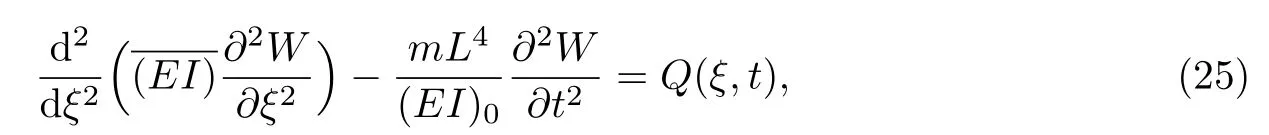
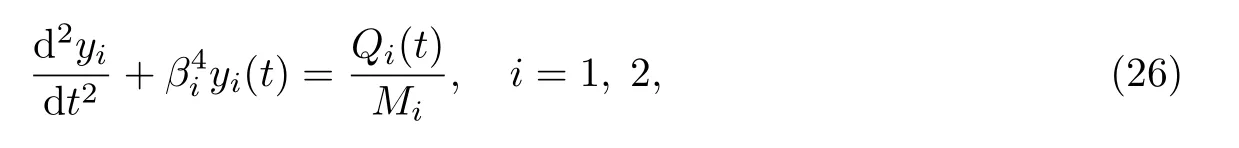

3 典型裂紋梁的自振頻率
3.1 簡支裂紋梁的動力特性
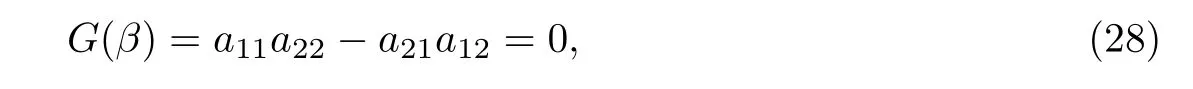
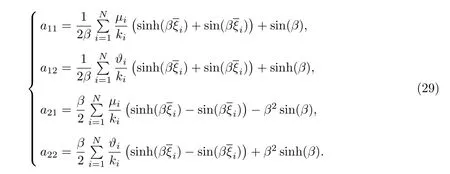

3.2 懸臂裂紋梁的動力特性

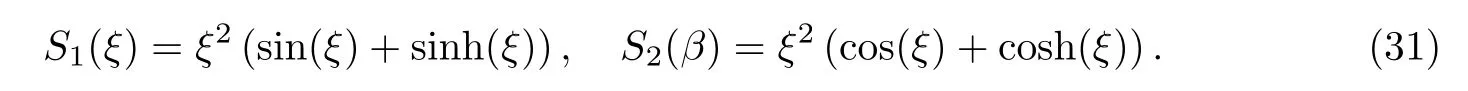



3.3 兩端固支裂紋梁的動力特性


4 裂紋梁的動力響應分析
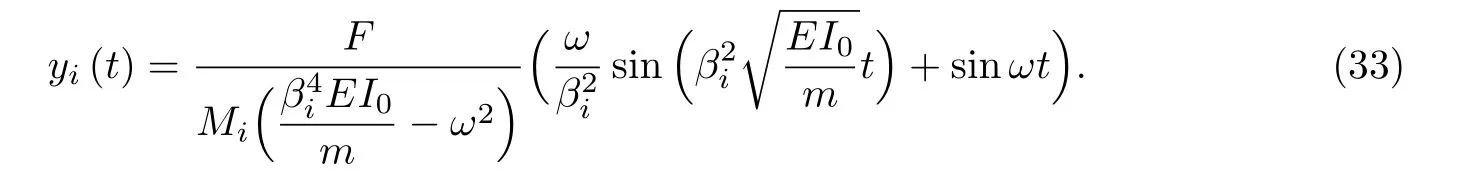
5 結束語

